19.2.1 一次函数(1) —正比例函数的图像与性质 学案(无答案) 2023--2024学年人教版八年级数学下册
文档属性
| 名称 | 19.2.1 一次函数(1) —正比例函数的图像与性质 学案(无答案) 2023--2024学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 14:29:49 | ||
图片预览

文档简介
19.2.1 一次函数(1)——正比例函数的图像与性质
班别:_____________ 姓名:_____________ 学号:____________ 日期:______________
【学习目标】
1.理解正比例函数的概念;
2.经历用函数解析式表示函数关系的过程,进一步发展符号意识;经历从一类具体函数中抽象出正比例函数概念的过程,发展数学抽象概括能力.
【学习重点】
正比例函数的概念.
【学习过程】
新知探究
思考:下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式.
(1)圆的周长 l 随半径 r 的变化而变化;
(2)铁的密度为7.8 g/cm3,铁块的质量 m(单位:g)随它的体积 V(单位:cm3)的变化而变化;
(3)每个练习本的厚度为0.5 cm,练习本摞在一起的总厚度 h(单位:cm)随练习本的本数 n 变化而变化;
(4)冷冻一个0 ℃ 的物体,使它每分下降2 ℃,物体的温度 T(单位:℃)随冷冻时间 t(单位:min)的变化而变化.
观察这些函数关系式,这些函数都是常数与自变量的________的形式。
归纳: 一般地,形如_________(_______________)的函数,叫做正比例函数,其中,k叫做__________.
试一试:下列式子中:①;②;③;④;⑤;⑥ ,表示y是x的正比例函数的有_________(填序号).
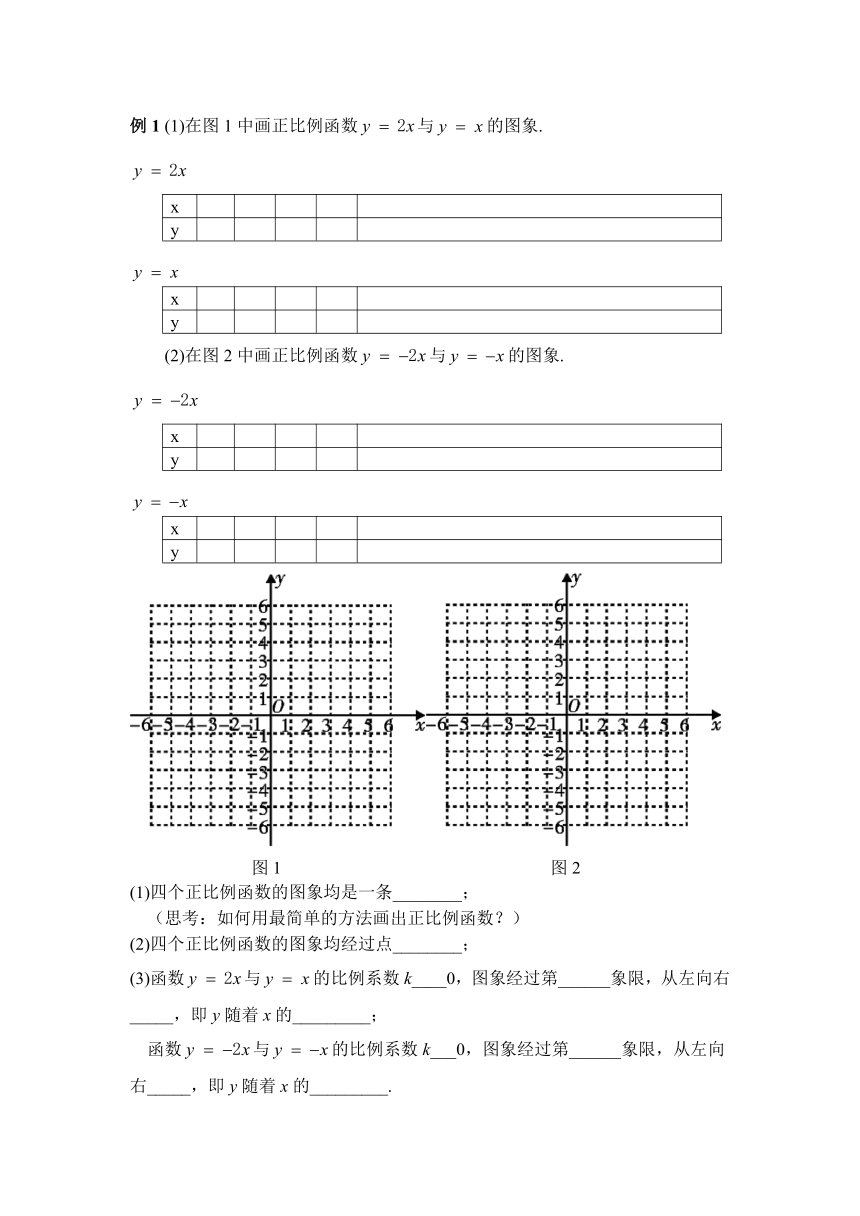
例1 (1)在图1中画正比例函数与的图象.
x
y
x
y
(2)在图2中画正比例函数与的图象.
x
y
x
y
图1 图2
(1)四个正比例函数的图象均是一条________;
(思考:如何用最简单的方法画出正比例函数?)
(2)四个正比例函数的图象均经过点________;
(3)函数与的比例系数k____0,图象经过第______象限,从左向右_____,即y随着x的_________;
函数与的比例系数k___0,图象经过第______象限,从左向右_____,即y随着x的_________.
归纳:
同步导练1
1.已知正比例函数,其中k<0,则函数图象是 ( )
A. B. C. D.
2.已知函数的函数值随x的增大而增大,则函数的图象经过 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
3.正比例函数的图象是一条_______,当k=3时,直线y=kx过第_______象限,y随x的增大而_______.
4.写出一个图象经过第一、三象限的正比例函数:_____________________.
例2
(1)正比例函数的图象经过一、三象限,则m的取值范围是________.
(2)函数的图象经过(3,-6),则k =_____,这个正比例函数的解析式是__________.
同步导练2
1.正比例函数的图象经过二、四象限,m的取值范围是___________.
2.已知正比例函数,如果y随着x增大而减小,则a的取值范围是___________.
3.如图,正比例函数图象经过点A,该函数解析式是_______.
4.已知函数 (k≠0),当x=3时,y=6,求这个函数的解析式.
当堂检测
(A组)
1.下列式子中,表示y是x的正比例函数的有________
(1) (2) (3) (4)
2.用你认为最简单的方法画出下列函数图像:(1) ;(2) .
(B组)
4.点P(1,y1),Q(-2,y2)是直线上的两点,则y1与y2的大小关系是y1_______y2.
(C组)
4.若正比例函数,y随着x的增大而减小,则m的值是_______.
5.如图,三个正比例函数的图象分别对应的解析式:① ,② ,③ ,将a,b,c从小到大排列并用“<”连接为___________.
班别:_____________ 姓名:_____________ 学号:____________ 日期:______________
【学习目标】
1.理解正比例函数的概念;
2.经历用函数解析式表示函数关系的过程,进一步发展符号意识;经历从一类具体函数中抽象出正比例函数概念的过程,发展数学抽象概括能力.
【学习重点】
正比例函数的概念.
【学习过程】
新知探究
思考:下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式.
(1)圆的周长 l 随半径 r 的变化而变化;
(2)铁的密度为7.8 g/cm3,铁块的质量 m(单位:g)随它的体积 V(单位:cm3)的变化而变化;
(3)每个练习本的厚度为0.5 cm,练习本摞在一起的总厚度 h(单位:cm)随练习本的本数 n 变化而变化;
(4)冷冻一个0 ℃ 的物体,使它每分下降2 ℃,物体的温度 T(单位:℃)随冷冻时间 t(单位:min)的变化而变化.
观察这些函数关系式,这些函数都是常数与自变量的________的形式。
归纳: 一般地,形如_________(_______________)的函数,叫做正比例函数,其中,k叫做__________.
试一试:下列式子中:①;②;③;④;⑤;⑥ ,表示y是x的正比例函数的有_________(填序号).
例1 (1)在图1中画正比例函数与的图象.
x
y
x
y
(2)在图2中画正比例函数与的图象.
x
y
x
y
图1 图2
(1)四个正比例函数的图象均是一条________;
(思考:如何用最简单的方法画出正比例函数?)
(2)四个正比例函数的图象均经过点________;
(3)函数与的比例系数k____0,图象经过第______象限,从左向右_____,即y随着x的_________;
函数与的比例系数k___0,图象经过第______象限,从左向右_____,即y随着x的_________.
归纳:
同步导练1
1.已知正比例函数,其中k<0,则函数图象是 ( )
A. B. C. D.
2.已知函数的函数值随x的增大而增大,则函数的图象经过 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
3.正比例函数的图象是一条_______,当k=3时,直线y=kx过第_______象限,y随x的增大而_______.
4.写出一个图象经过第一、三象限的正比例函数:_____________________.
例2
(1)正比例函数的图象经过一、三象限,则m的取值范围是________.
(2)函数的图象经过(3,-6),则k =_____,这个正比例函数的解析式是__________.
同步导练2
1.正比例函数的图象经过二、四象限,m的取值范围是___________.
2.已知正比例函数,如果y随着x增大而减小,则a的取值范围是___________.
3.如图,正比例函数图象经过点A,该函数解析式是_______.
4.已知函数 (k≠0),当x=3时,y=6,求这个函数的解析式.
当堂检测
(A组)
1.下列式子中,表示y是x的正比例函数的有________
(1) (2) (3) (4)
2.用你认为最简单的方法画出下列函数图像:(1) ;(2) .
(B组)
4.点P(1,y1),Q(-2,y2)是直线上的两点,则y1与y2的大小关系是y1_______y2.
(C组)
4.若正比例函数,y随着x的增大而减小,则m的值是_______.
5.如图,三个正比例函数的图象分别对应的解析式:① ,② ,③ ,将a,b,c从小到大排列并用“<”连接为___________.
