2024年高考物理复习专题 课件★★带电粒子在交变场中的运动 课件(共36张PPT)
文档属性
| 名称 | 2024年高考物理复习专题 课件★★带电粒子在交变场中的运动 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-10 14:46:20 | ||
图片预览








文档简介
(共36张PPT)
带电粒子在交变场中的运动
2024年高考物理复习专题 课件★★
考点一
带电粒子在交变电场中的运动
处理带电粒子在交变电场中运动的问题时,对带电粒子进行受力分析,判断带电粒子在每一段的运动情况,画出粒子在电场方向的v-t图像、运动示意图,结合图像去分析粒子的运动情况,在v-t图像中,图线与t轴所围面积表示沿电场方向粒子的位移。带电粒子在交变电场中沿电场强度方向的运动常见的v-t图像如图所示。
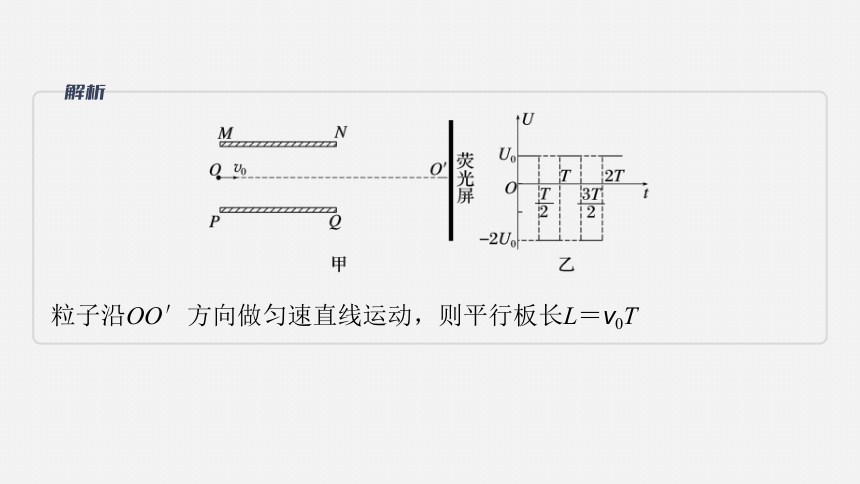
(2023·江苏扬州市高邮中学模拟)如图甲,真空中水平放置的平行金属板MN、PQ间所加交变电压U随时间t的变化图像如图乙所示,U0已知。距离平行板右侧有一足够大的荧光屏,荧光屏距平行板右侧的距离与平行板的长度相等,粒子打到荧光屏上形成亮斑。现有大量质量为m、电荷量为+q的粒子以初速度v0平行于两板沿中线OO′持续不断地射入两板间。已知t=0时刻进入两板间的粒子穿过两板的时间等于所加交变电压的周期T,出射方向偏转了53°,所有粒子均可以从板间射出,忽略电场的边缘效应及重力的影响,sin 53°=0.8,cos 53°=0.6。求:
(1)平行板的长度;
例1
答案 v0T
粒子沿OO′方向做匀速直线运动,则平行板长L=v0T
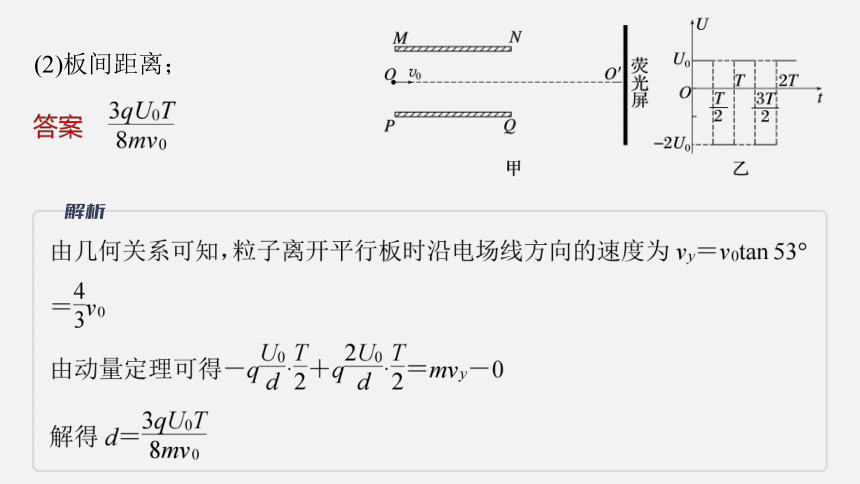
(2)板间距离;
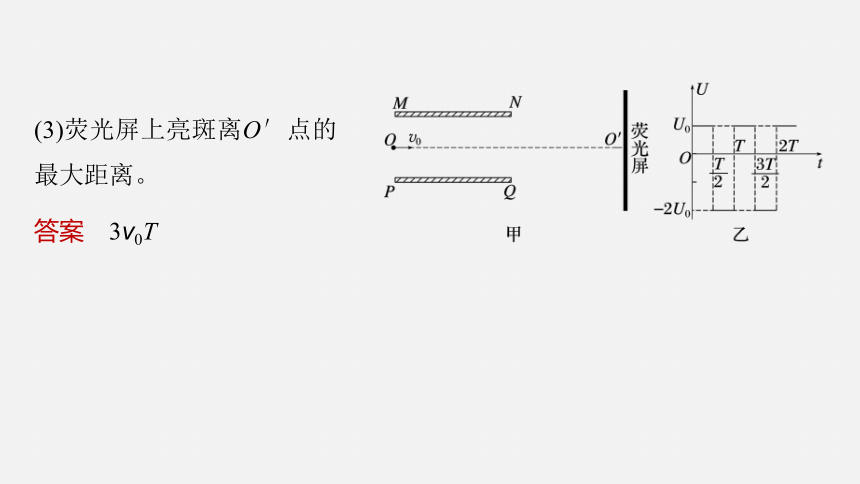
(3)荧光屏上亮斑离O′点的最大距离。
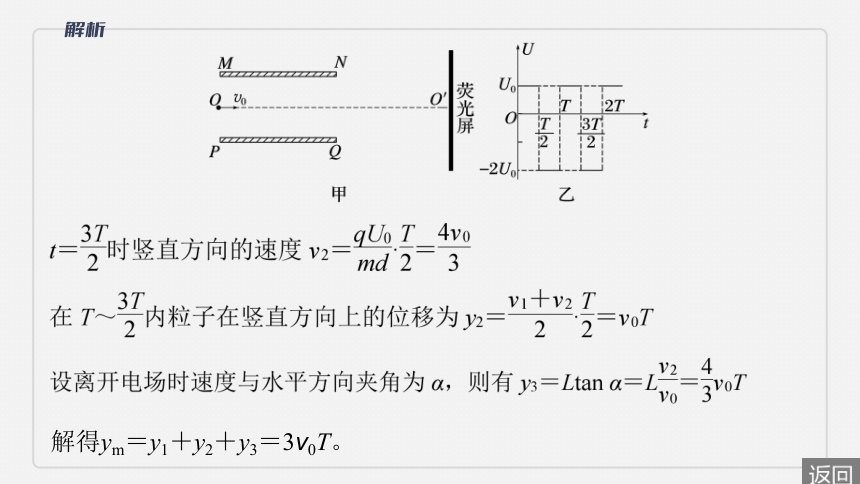
答案 3v0T
解得ym=y1+y2+y3=3v0T。
考点二
带电粒子在交变电、磁场中的运动
此类问题是场在时间上的组合,电场或磁场往往具有周期性,粒子的运动也往往具有周期性。这种情况下要仔细分析带电粒子的受力情况和运动过程,弄清楚带电粒子在每一时间段内在电场、磁场中各处于什么状态,做什么运动,画出一个周期内的运动轨迹,确定带电粒子的运动过程,选择合适的规律进行解题。
如图甲所示,水平放置的平行金属板P和Q相距为d,两板间存在周期性变化的电场或磁场。P、Q间的电势差UPQ随时间的变化规律如图乙所示,磁感应强度B随时间变化的规律如图丙所示,磁场方向垂直纸面向里为正方向。t=0时刻,一质量为m、电荷量为+q的粒子(不计重力),以初速度v0由P板左端靠近板面的位置,沿平行于板面的方向射入两板之间,q、m、d、v0、U0为已知量。
(1)若仅存在交变电场,要使粒子
飞到Q板时,速度方向恰好与Q板
相切,求交变电场周期T;
例2
当粒子飞到Q板时的速度方向恰与Q板相切时,竖直速度为零,设加速度为a,
半个周期内,粒子向上运动的距离为
若要使粒子能垂直打到Q板上,在交变磁场的半个周期内,设粒子轨迹的圆心角为90°+θ,如图所示,由几何关系得r+2rsin θ=d
则粒子打到上极板的位置距出发点的水平距离为
高考预测
如图甲所示,在y轴左侧存在沿x轴正方向的匀强电场,在y轴右侧的矩形虚线空间存在垂直于纸面的周期性的磁场,磁感应强度大小为 ,磁场上边界在y=2a处,下边界在y=-2a处,右边界在x=3a处,磁场的变化规律如图乙所示,规定垂直纸面向里的方向为磁场的正方向。t=0时刻,一质量为m、电荷量为q的带正电粒子从位置坐标为(a,2a)的A点以速度v沿y轴负方向射入磁场,若粒子恰能垂直打到放置在下边界处的水平挡板上的B点(图中B点未标出),并经碰撞后原速率反弹(不计碰撞时间和
电荷量的变化),最终粒子会从A
点垂直上边界向上射出,离开磁
场区域。不计粒子重力,不考虑
变化的磁场所产生的电场。求:
(1)带电粒子在磁场中的运动半径与运动周期;
可知粒子到达x轴时开始在磁场中做圆周运动,设运动半径为R,由洛伦兹力提供向心力,则有
(2)若使粒子从A点运动到B点的时间最短,图乙中T0的最小值;
(3)T0取第(2)问的数值,使带电粒子从与B点碰后运动到A点的时间最短,则此条件下所加的电场强度E的大小。
加速度方向与粒子运动方向相反,做匀减速直线运动,经t1时间返回,又以原速度大小垂直y轴射入磁场
带电粒子从与B点碰后运动到A点有最短时间,即粒子在一个周期内在x轴下方磁场和电场中运动,然后在x轴上方做匀速直线运动,直到再次从A点垂直上边界射出磁场。
专题强化练
1
2
1.实验小组用如图甲所示装置研究带电粒子在两个平行金属板间的运动,已知板长为L,两板间距d未知,将放射源P行金属板,放射出的带电粒子沿平行金属板A、B的中轴线MN射入板间,平行金属板A、B间加有如图乙所示的交变电压,已知电压U0,周期T未知,当电压稳定时,板间是匀强电场。质量为m、电荷量为q的粒子以 v0的速率在T时刻从M点进入板间, T时刻离开金属板,运动过程中恰好不与金属板碰撞(粒子重力忽略不计)。求:平行板A、B的
间距d是多少?
1
2
规定向下为正方向,粒子在竖直方向做匀加速直线运动,设A、B两板间距为d
1
2
再减速为零后反向做加速运动,时间为
1
2
1
2
2.如图甲所示的xOy平面内存在大小随时间周期性变化的匀强磁场和匀强电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁感应强度的正方向,沿y轴负方向为电场强度的正方向)。在t=0时刻由原点O发射一个初速度大小为v0、方向沿y轴正方向的带正电粒子,粒子的比荷 ,v0、B0、E0、t0均为已知量,不计粒子受到的重力。
(1)求在0~t0内粒子运动轨迹
的半径;
1
2
1
2
(2)求t=2t0时,粒子的位置坐标;
1
2
若粒子在磁场中做完整的圆周运动,
解得T=2t0
1
2
3
4
故t=2t0时,粒子的位置坐标为
1
2
(3)若粒子在t=25t0时首次回到坐标原点,求电场强度E0与磁感应强度B0的大小关系。
1
2
如图所示,带电粒子在x轴上方做圆周运动的轨道半径为
由几何关系可知,要使粒子经过原点,则必须满足
带电粒子在交变场中的运动
2024年高考物理复习专题 课件★★
考点一
带电粒子在交变电场中的运动
处理带电粒子在交变电场中运动的问题时,对带电粒子进行受力分析,判断带电粒子在每一段的运动情况,画出粒子在电场方向的v-t图像、运动示意图,结合图像去分析粒子的运动情况,在v-t图像中,图线与t轴所围面积表示沿电场方向粒子的位移。带电粒子在交变电场中沿电场强度方向的运动常见的v-t图像如图所示。
(2023·江苏扬州市高邮中学模拟)如图甲,真空中水平放置的平行金属板MN、PQ间所加交变电压U随时间t的变化图像如图乙所示,U0已知。距离平行板右侧有一足够大的荧光屏,荧光屏距平行板右侧的距离与平行板的长度相等,粒子打到荧光屏上形成亮斑。现有大量质量为m、电荷量为+q的粒子以初速度v0平行于两板沿中线OO′持续不断地射入两板间。已知t=0时刻进入两板间的粒子穿过两板的时间等于所加交变电压的周期T,出射方向偏转了53°,所有粒子均可以从板间射出,忽略电场的边缘效应及重力的影响,sin 53°=0.8,cos 53°=0.6。求:
(1)平行板的长度;
例1
答案 v0T
粒子沿OO′方向做匀速直线运动,则平行板长L=v0T
(2)板间距离;
(3)荧光屏上亮斑离O′点的最大距离。
答案 3v0T
解得ym=y1+y2+y3=3v0T。
考点二
带电粒子在交变电、磁场中的运动
此类问题是场在时间上的组合,电场或磁场往往具有周期性,粒子的运动也往往具有周期性。这种情况下要仔细分析带电粒子的受力情况和运动过程,弄清楚带电粒子在每一时间段内在电场、磁场中各处于什么状态,做什么运动,画出一个周期内的运动轨迹,确定带电粒子的运动过程,选择合适的规律进行解题。
如图甲所示,水平放置的平行金属板P和Q相距为d,两板间存在周期性变化的电场或磁场。P、Q间的电势差UPQ随时间的变化规律如图乙所示,磁感应强度B随时间变化的规律如图丙所示,磁场方向垂直纸面向里为正方向。t=0时刻,一质量为m、电荷量为+q的粒子(不计重力),以初速度v0由P板左端靠近板面的位置,沿平行于板面的方向射入两板之间,q、m、d、v0、U0为已知量。
(1)若仅存在交变电场,要使粒子
飞到Q板时,速度方向恰好与Q板
相切,求交变电场周期T;
例2
当粒子飞到Q板时的速度方向恰与Q板相切时,竖直速度为零,设加速度为a,
半个周期内,粒子向上运动的距离为
若要使粒子能垂直打到Q板上,在交变磁场的半个周期内,设粒子轨迹的圆心角为90°+θ,如图所示,由几何关系得r+2rsin θ=d
则粒子打到上极板的位置距出发点的水平距离为
高考预测
如图甲所示,在y轴左侧存在沿x轴正方向的匀强电场,在y轴右侧的矩形虚线空间存在垂直于纸面的周期性的磁场,磁感应强度大小为 ,磁场上边界在y=2a处,下边界在y=-2a处,右边界在x=3a处,磁场的变化规律如图乙所示,规定垂直纸面向里的方向为磁场的正方向。t=0时刻,一质量为m、电荷量为q的带正电粒子从位置坐标为(a,2a)的A点以速度v沿y轴负方向射入磁场,若粒子恰能垂直打到放置在下边界处的水平挡板上的B点(图中B点未标出),并经碰撞后原速率反弹(不计碰撞时间和
电荷量的变化),最终粒子会从A
点垂直上边界向上射出,离开磁
场区域。不计粒子重力,不考虑
变化的磁场所产生的电场。求:
(1)带电粒子在磁场中的运动半径与运动周期;
可知粒子到达x轴时开始在磁场中做圆周运动,设运动半径为R,由洛伦兹力提供向心力,则有
(2)若使粒子从A点运动到B点的时间最短,图乙中T0的最小值;
(3)T0取第(2)问的数值,使带电粒子从与B点碰后运动到A点的时间最短,则此条件下所加的电场强度E的大小。
加速度方向与粒子运动方向相反,做匀减速直线运动,经t1时间返回,又以原速度大小垂直y轴射入磁场
带电粒子从与B点碰后运动到A点有最短时间,即粒子在一个周期内在x轴下方磁场和电场中运动,然后在x轴上方做匀速直线运动,直到再次从A点垂直上边界射出磁场。
专题强化练
1
2
1.实验小组用如图甲所示装置研究带电粒子在两个平行金属板间的运动,已知板长为L,两板间距d未知,将放射源P行金属板,放射出的带电粒子沿平行金属板A、B的中轴线MN射入板间,平行金属板A、B间加有如图乙所示的交变电压,已知电压U0,周期T未知,当电压稳定时,板间是匀强电场。质量为m、电荷量为q的粒子以 v0的速率在T时刻从M点进入板间, T时刻离开金属板,运动过程中恰好不与金属板碰撞(粒子重力忽略不计)。求:平行板A、B的
间距d是多少?
1
2
规定向下为正方向,粒子在竖直方向做匀加速直线运动,设A、B两板间距为d
1
2
再减速为零后反向做加速运动,时间为
1
2
1
2
2.如图甲所示的xOy平面内存在大小随时间周期性变化的匀强磁场和匀强电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁感应强度的正方向,沿y轴负方向为电场强度的正方向)。在t=0时刻由原点O发射一个初速度大小为v0、方向沿y轴正方向的带正电粒子,粒子的比荷 ,v0、B0、E0、t0均为已知量,不计粒子受到的重力。
(1)求在0~t0内粒子运动轨迹
的半径;
1
2
1
2
(2)求t=2t0时,粒子的位置坐标;
1
2
若粒子在磁场中做完整的圆周运动,
解得T=2t0
1
2
3
4
故t=2t0时,粒子的位置坐标为
1
2
(3)若粒子在t=25t0时首次回到坐标原点,求电场强度E0与磁感应强度B0的大小关系。
1
2
如图所示,带电粒子在x轴上方做圆周运动的轨道半径为
由几何关系可知,要使粒子经过原点,则必须满足
同课章节目录
