【全国百强校】湖南省长郡中学高中物理必修一课件:第三章 第五节 《力的分解》(共41张PPT)
文档属性
| 名称 | 【全国百强校】湖南省长郡中学高中物理必修一课件:第三章 第五节 《力的分解》(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-10-16 00:00:00 | ||
图片预览








文档简介
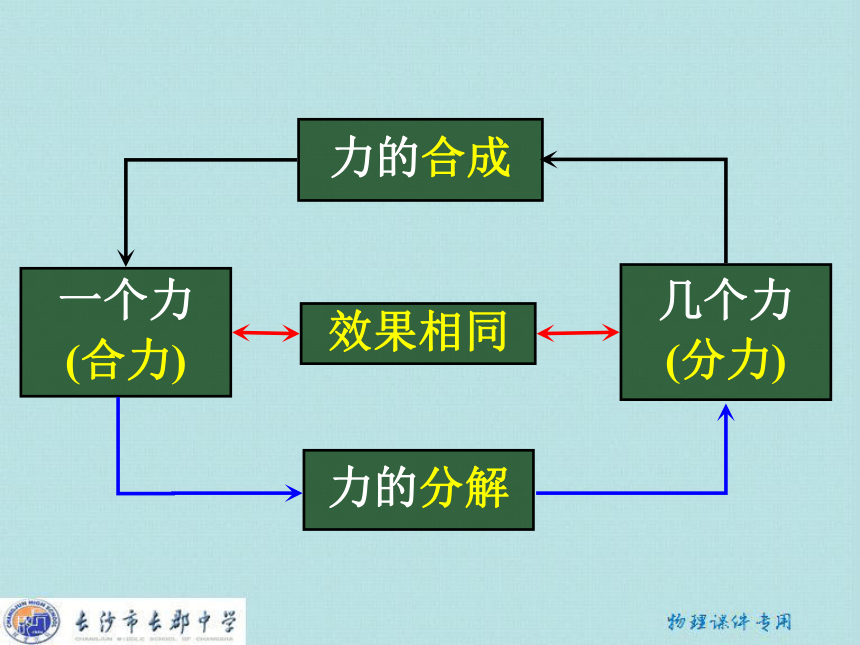
课件41张PPT。力的分解一、力的分解一、力的分解 【定义】求一个力的分力的过程叫做力
的分解。 一、力的分解 【牢记】力的分解是力的合成的逆运算。 【定义】求一个力的分力的过程叫做力
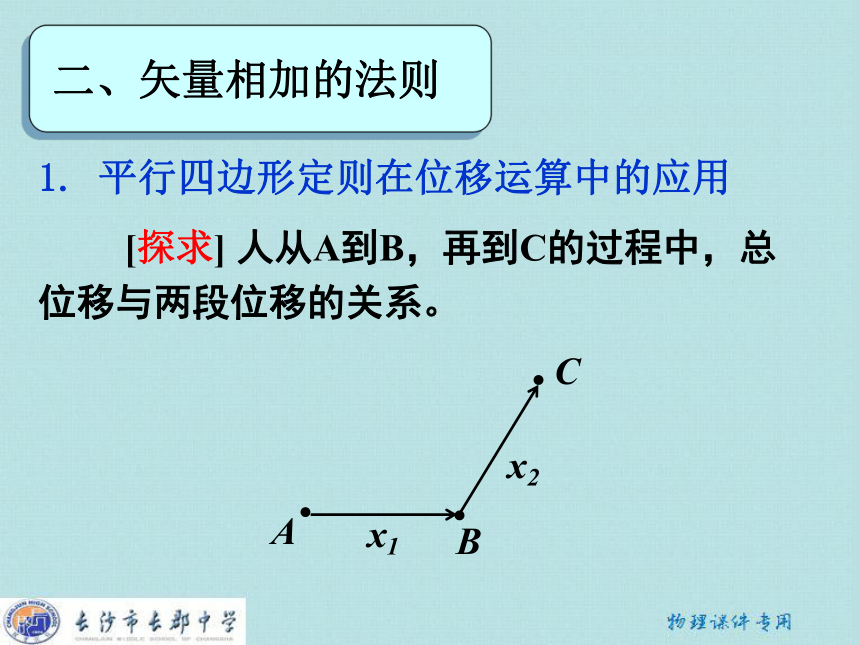
的分解。 二、矢量相加的法则二、矢量相加的法则1. 平行四边形定则在位移运算中的应用二、矢量相加的法则1. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。二、矢量相加的法则AB1. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则ABx11. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
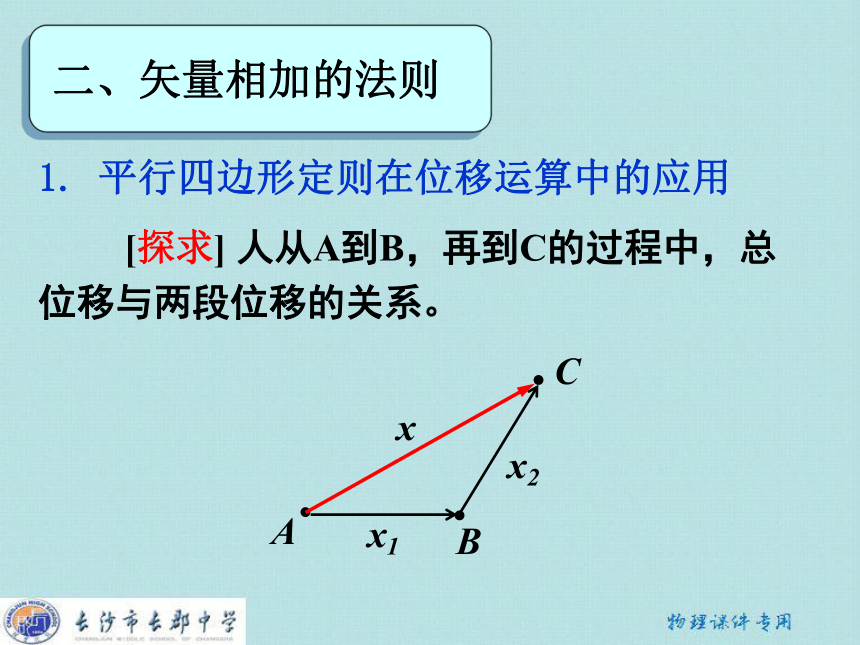
位移与两段位移的关系。C二、矢量相加的法则ABx1x21. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则1. 平行四边形定则在位移运算中的应用ABx1x2x [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则1. 平行四边形定则在位移运算中的应用ABx1x2x [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C2. 三角形定则把两个矢量首尾连接求出合矢量的方法。2. 三角形定则[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?v1v2把两个矢量首尾连接求出合矢量的方法。2. 三角形定则[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量 矢量: 有大小,又有方向,相加时遵循平
行四边形定则。
[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量 矢量: 有大小,又有方向,相加时遵循平
行四边形定则。
标量: 有大小,没有方向,求和时按算术
法则相加。4. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。F4. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F24. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F2F3F44. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F2F3F4F5F64. 若没有其它限制,同一个力可以分解为
无数对大小、方向不同的分力。三、根据力的作用效果确定两分力的方向实际
问题力的作
用效果作平行
四边形用数学
知识解力的大小化
为线段长短力的分
解定则方法小结确定
两分力 方向四、将一个已知力力分解的几种情况 四、将一个已知力力分解的几种情况 1. 已知两个分力方向四、将一个已知力力分解的几种情况 1. 已知两个分力方向四、将一个已知力力分解的几种情况 1. 已知两个分力方向[结论] 唯一的一组解 2. 已知其中一个分力F1的大小和方向2. 已知其中一个分力F1的大小和方向2. 已知其中一个分力F1的大小和方向[结论] 唯一的一组解五、正交分解 把力沿两个互相垂直的方向进行分 解的方法叫做力的正交分解法。正交分 解法是在平行四边形定则的基础上发展 起来的,其目的是用代数运算来解决矢 量运算。 正交分解法在求解不在一条直线上 的多个力的合力时显示出较大优越性。 这类问题若用平行四边形定则直接
求解,不管采用作图法还是计算法,都
必须两两合成,一次接一次地求部分合
力的大小和方向,十分麻烦。所以我们
要深刻理解正交分解法的思想,并会熟
练应用它来解决问题。利用正交分解法求合力的一般步骤是: (1)建立直角坐标系xOy;
(2)将各力沿x、y两坐标轴依次分解为互相 垂直的两个分力;
(3)分别求出x、y两坐标轴上各分力的合力 Fx、Fy;
(4)求出Fx和Fy的合力F,其大小为:
方向为与x轴的夹角: 值得注意的是:建立坐标系时,
一般选共点力作用线的交点为坐标轴
的原点,并尽可能使较多的力落在坐
标轴上,这样可以减少需要分解的力
的数目,简化运算过程。典例精析 [例]一个质量m=10kg
的物体放在水平地面上,
物体与地面间的动摩擦因
数μ=0.4。轻弹簧的一端系在物体上,如图
所示,当用力F与水平方向成θ=37°角拉弹
簧时,弹簧的长度由10cm伸长到13cm,物体
沿水平面做匀速直线运动,g取10m/s2,求弹簧
的劲度系数为多少?(已知sin37°=0.6,
cos37°=0.8) [解析] 物体的受力分析如图所示,将F
分解为F1和F2,因物体做匀速直线运动,所
以F1=Ff,即
F·cosθ=μFN
又mg=F2+FN,F=kx
由以上各式得:
k=μmg/x(cosθ+μsinθ)
=0.4×10×10/0.03 ×(0.8 +0.4 ×0.6)N/m
≈1282.05N/m。
的分解。 一、力的分解 【牢记】力的分解是力的合成的逆运算。 【定义】求一个力的分力的过程叫做力
的分解。 二、矢量相加的法则二、矢量相加的法则1. 平行四边形定则在位移运算中的应用二、矢量相加的法则1. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。二、矢量相加的法则AB1. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则ABx11. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则ABx1x21. 平行四边形定则在位移运算中的应用 [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则1. 平行四边形定则在位移运算中的应用ABx1x2x [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C二、矢量相加的法则1. 平行四边形定则在位移运算中的应用ABx1x2x [探求] 人从A到B,再到C的过程中,总
位移与两段位移的关系。C2. 三角形定则把两个矢量首尾连接求出合矢量的方法。2. 三角形定则[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?v1v2把两个矢量首尾连接求出合矢量的方法。2. 三角形定则[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量 矢量: 有大小,又有方向,相加时遵循平
行四边形定则。
[说一说] 一个物体的速度v1在一小段时间内发 生了变化,变成了v2,你能根据三角 形定则找出变化量?v吗?2. 三角形定则把两个矢量首尾连接求出合矢量的方法。3. 矢量和标量 矢量: 有大小,又有方向,相加时遵循平
行四边形定则。
标量: 有大小,没有方向,求和时按算术
法则相加。4. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。F4. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F24. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F2F3F44. 若没有其它限制,同一个力可以分解为 无数对大小、方向不同的分力。FF1F2F3F4F5F64. 若没有其它限制,同一个力可以分解为
无数对大小、方向不同的分力。三、根据力的作用效果确定两分力的方向实际
问题力的作
用效果作平行
四边形用数学
知识解力的大小化
为线段长短力的分
解定则方法小结确定
两分力 方向四、将一个已知力力分解的几种情况 四、将一个已知力力分解的几种情况 1. 已知两个分力方向四、将一个已知力力分解的几种情况 1. 已知两个分力方向四、将一个已知力力分解的几种情况 1. 已知两个分力方向[结论] 唯一的一组解 2. 已知其中一个分力F1的大小和方向2. 已知其中一个分力F1的大小和方向2. 已知其中一个分力F1的大小和方向[结论] 唯一的一组解五、正交分解 把力沿两个互相垂直的方向进行分 解的方法叫做力的正交分解法。正交分 解法是在平行四边形定则的基础上发展 起来的,其目的是用代数运算来解决矢 量运算。 正交分解法在求解不在一条直线上 的多个力的合力时显示出较大优越性。 这类问题若用平行四边形定则直接
求解,不管采用作图法还是计算法,都
必须两两合成,一次接一次地求部分合
力的大小和方向,十分麻烦。所以我们
要深刻理解正交分解法的思想,并会熟
练应用它来解决问题。利用正交分解法求合力的一般步骤是: (1)建立直角坐标系xOy;
(2)将各力沿x、y两坐标轴依次分解为互相 垂直的两个分力;
(3)分别求出x、y两坐标轴上各分力的合力 Fx、Fy;
(4)求出Fx和Fy的合力F,其大小为:
方向为与x轴的夹角: 值得注意的是:建立坐标系时,
一般选共点力作用线的交点为坐标轴
的原点,并尽可能使较多的力落在坐
标轴上,这样可以减少需要分解的力
的数目,简化运算过程。典例精析 [例]一个质量m=10kg
的物体放在水平地面上,
物体与地面间的动摩擦因
数μ=0.4。轻弹簧的一端系在物体上,如图
所示,当用力F与水平方向成θ=37°角拉弹
簧时,弹簧的长度由10cm伸长到13cm,物体
沿水平面做匀速直线运动,g取10m/s2,求弹簧
的劲度系数为多少?(已知sin37°=0.6,
cos37°=0.8) [解析] 物体的受力分析如图所示,将F
分解为F1和F2,因物体做匀速直线运动,所
以F1=Ff,即
F·cosθ=μFN
又mg=F2+FN,F=kx
由以上各式得:
k=μmg/x(cosθ+μsinθ)
=0.4×10×10/0.03 ×(0.8 +0.4 ×0.6)N/m
≈1282.05N/m。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
