第四章《三角形》复习试题 2023--2024学年北师大版七年级数学下册(含答案)
文档属性
| 名称 | 第四章《三角形》复习试题 2023--2024学年北师大版七年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 17:07:14 | ||
图片预览




文档简介
北师大版数学七年级下
第四单元《三角形》复习试题
一.选择题(共10小题)
1.下列每组数分别表示3根小木棒的长度(单位:cm),其中能搭成三角形的是( )
A.3,7,10 B.6,7,8 C.7,7,14 D.5,7,13
2.如图所示,为估计池塘两岸A,B间的距离,小华在池塘一侧选取一点P,测得PA=8m,PB=6m,那么A,B之间的距离不可能是( )
A.8m B.10m C.12m D.14m
3.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
4.下列说法正确的是( )
A.三角形的三条中线交于一点 B.三角形的三条高都在三角形内部
C.三角形不一定具有稳定性 D.三角形的角平分线可能在三角形的内部或外部
5.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=130°,则∠A的度数为( )
A.80° B.70° C.60° D.45°
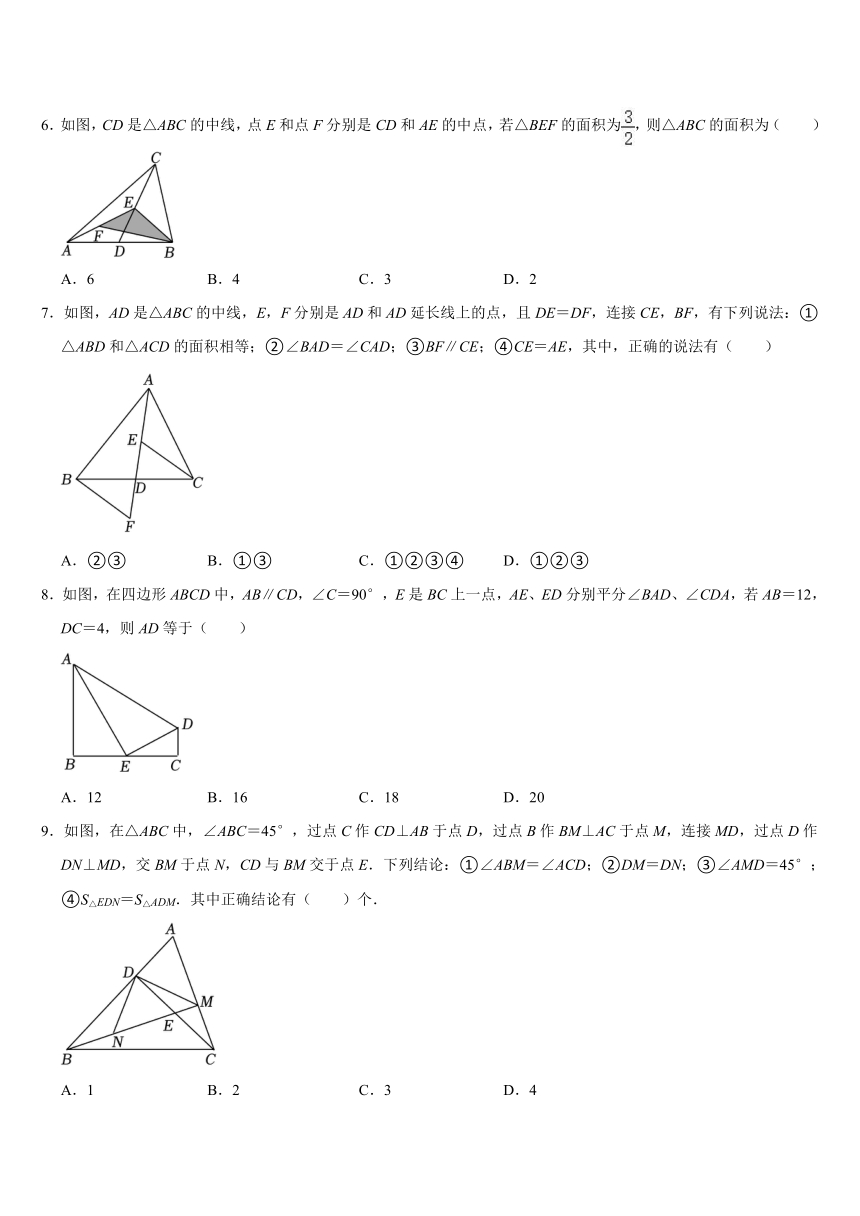
6.如图,CD是△ABC的中线,点E和点F分别是CD和AE的中点,若△BEF的面积为,则△ABC的面积为( )
A.6 B.4 C.3 D.2
7.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接CE,BF,有下列说法:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=AE,其中,正确的说法有( )
A.②③ B.①③ C.①②③④ D.①②③
8.如图,在四边形ABCD中,AB∥CD,∠C=90°,E是BC上一点,AE、ED分别平分∠BAD、∠CDA,若AB=12,DC=4,则AD等于( )
A.12 B.16 C.18 D.20
9.如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N,CD与BM交于点E.下列结论:①∠ABM=∠ACD;②DM=DN;③∠AMD=45°;④S△EDN=S△ADM.其中正确结论有( )个.
A.1 B.2 C.3 D.4
10.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
二.填空题(共8小题)
11.如图,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2022与∠A2022CD的平分线相交于点A2023,得∠A2023,则∠A2023度数是 .
12.△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
13.在△ABC是AB=5,AC=3,BC边的中线AD的取值范围是 .
14.纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为 .
15.已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|+|c﹣a﹣b|= .
16.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
17.如图,在△ABC与△ADE中,E在BC边上,AD=AB,AE=AC,DE=BC,若∠1=25°,则∠DAB= °,∠2= °.
18.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①AD=BE;②∠AOB=70°;③△CPQ为等边三角形;④△APC≌△BQC.其中正确的有 .(注:把正确的答案序号都写上)
三.解答题(共10小题)
19.如图,点A,D,B,E在同一直线上,AD=BE,AC=DF,∠A=∠BDF,求证:BC∥EF.
20.如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:∠AEO=∠CFO.
21.如图,点A、B、C、D在一条直线上,点E、F分别在AD的两侧,连接AF、CF、BE、DE,BE∥CF,AB=CD,∠E=∠F.求证:BE=CF.
22.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
24.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,BE=4,求AB的长.
25.如图,点B、F、C、E在一条直线上,OA=OD,AC∥FD,AD交BE于O.
(1)求证:△ACO≌△DFO;
(2)若BF=CE.求证:AB∥DE.
26.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
27.如图,已知,AB=AC,点D、E分别在AC、AB上,且AE=AD,∠B=∠C,连接EC,BD、EC交BD于点M、连接AM.
(1)求证:△EBM≌△DCM;
(2)嘉琪说:“若S△BEM=S△ADM,则E是AB的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.
28.已知,△ABC中,CA=CB,∠ACB=90°,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.
(1)如图1,求证:EF=AE+BF;
(2)如图2,请直接写出EF,AE,BF之间的数量关系 ;
(3)在(2)的条件下,若BF=3AE,EF=4,求△BFC的面积.
参考答案
一.选择题(共10小题)
1.B.
2.D.
3.A.
4.A.
5.A.
6.A.
7.B.
8.B.
9.D.
10.B.
二.填空题(共8小题)
11.x°.
12.直角.
13.1<AD<4.
14.60°.
15.a+3b﹣c.
16.7.
17.25,25.
18.①③④.
三.解答题(共10小题)
19.如图,点A,D,B,E在同一直线上,AD=BE,AC=DF,∠A=∠BDF,求证:BC∥EF.
证明:∵点A,D,B,E在同一直线上,AD=BE,
∴AD+DB=BE+DB,
∴AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠ABC=∠E,
∴BC∥EF.
20.如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:∠AEO=∠CFO.
证明:∵BF=DE,
∴BF﹣EF=DE﹣EF,
即BE=DF,
在△ABE和△DFC中,
,
∴△ABE≌△CDF(SSS),
∴∠AEB=∠CFD,
∴∠AEO=∠CFO.
21.如图,点A、B、C、D在一条直线上,点E、F分别在AD的两侧,连接AF、CF、BE、DE,BE∥CF,AB=CD,∠E=∠F.求证:BE=CF.
证明:BE∥CF,
∴∠EBD=∠ACF,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB,
在△DBE和△ACF中,
,
∴△DBE≌△ACF(AAS),
∴BE=CF.
22.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.
证明:∵AC=BC,
∴∠A=∠B,
∵AC=BC BC=BD,
∴AC=BD,
∵∠CDB=∠A+∠ACD=∠CDE+∠BDE,∠CDE=∠A,
∴∠ACD=∠BDE,
在△ACD与△BDE中,
,
∴△ACD≌△BDE(ASA),
∴CD=DE.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
(1)证明:∵AB∥CD,
∴∠BAE=∠FCD,
∵AF=CE,
∴AE=CF,
又∵AB=CD,
∴△ABE≌△CDF(SAS).
(2)解:∵∠BCE=30°,∠CBE=70°,
∴∠AEB=∠BCE+∠CBE=30°+70°=100°,
∵△ABE≌△CDF,
∴∠CFD=∠AEB=100°.
24.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,BE=4,求AB的长.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵∠AED=∠AFD=90°,AD=AD,DE=DF,
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF,
∵AC=20,CF=BE=4,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
25.如图,点B、F、C、E在一条直线上,OA=OD,AC∥FD,AD交BE于O.
(1)求证:△ACO≌△DFO;
(2)若BF=CE.求证:AB∥DE.
证明:(1)∵AC∥FD,
∴∠CAO=∠FDO,
在△ACO与△DFO中
,
∴△ACO≌△DFO(AAS);
(2)∵△ACO≌△DFO,
∴OF=OC,
∵BF=CE,
∴BO=EO,
在△ABO与△DEO中
,
∴△ABO≌△DEO(SAS),
∴∠B=∠E,
∴AB∥DE.
26.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
解:∵∠AEB=90°,AD⊥DC,BC⊥DC,
∴∠AEB=∠ADE=∠BCE=90°,
∴∠AED+∠DAE=90°,∠AED+∠BEC=90°,∠BEC+∠EBC=90°,
∴∠DAE=∠CEB,∠AED=∠EBC,
又∵AE=BE,
∴△ADE≌△ECB(ASA),
∴AD=CE,DE=BC,
又∵AD=150米,BC=350米,
∴DC=DE+CE=BC+AD=350+150=500(米).
答:两个排污口之间的水平距离DC为500米.
27.如图,已知,AB=AC,点D、E分别在AC、AB上,且AE=AD,∠B=∠C,连接EC,BD、EC交BD于点M、连接AM.
(1)求证:△EBM≌△DCM;
(2)嘉琪说:“若S△BEM=S△ADM,则E是AB的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.
(1)证明:∵AB=AE+BE,AC=AD+CD,
又∵AB=AC,AE=AD,
∴BE=CD,
在△EBM和△DCM中,
,
∴△EBM≌△DCM(AAS)
(2)解:嘉琪的说法正确,理由如下:
∵△EBM≌△DCM,
∴ME=MD,
在△AEM和△ADM中,
,
∴△AEM≌△ADM(SSS),
S△AEM=S△ADM;
∵S△BEM=S△ADM,
∴S△BEM=S△AEM,
过点M作MF⊥AB于点F,
则,
∴AE=BE,
即E是AB的中点.
28.已知,△ABC中,CA=CB,∠ACB=90°,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.
(1)如图1,求证:EF=AE+BF;
(2)如图2,请直接写出EF,AE,BF之间的数量关系 EF=BF﹣AE ;
(3)在(2)的条件下,若BF=3AE,EF=4,求△BFC的面积.
(1)证明:∵∠ACB=90°,
∴∠ECA+∠FCB=90°,
又∵AE⊥EF,BF⊥EF,
∴∠AEF=∠BFC=90°,
∴∠ECA+∠EAC=90°,
∴∠FCB=∠EAC,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∵EF=EC+CF,
∴EF=AE+BF;
(2)解:EF=BF﹣AE,理由如下:
∵∠AEC=∠CFB=90°,∠ACB=90°,
∴∠ACE+∠CAE=∠ACE+∠BCF=90°,
∴∠CAE=∠BCF
又∵AC=BC,
∴△CAE≌△BCF(AAS),
∴CE=BF,AE=CF,
∴EF=CE﹣CF=BF﹣AE,
即EF=BF﹣AE;
故答案为:EF=BF﹣AE;
(3)解:由(2)得EF=AE+BF且BF=3AE,
∴CE=3AE,
∵CF=AE,
∴EF=2AE=4,
∴AE=CF=2,BF=6,
∴△BFC的面积=.
第四单元《三角形》复习试题
一.选择题(共10小题)
1.下列每组数分别表示3根小木棒的长度(单位:cm),其中能搭成三角形的是( )
A.3,7,10 B.6,7,8 C.7,7,14 D.5,7,13
2.如图所示,为估计池塘两岸A,B间的距离,小华在池塘一侧选取一点P,测得PA=8m,PB=6m,那么A,B之间的距离不可能是( )
A.8m B.10m C.12m D.14m
3.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
4.下列说法正确的是( )
A.三角形的三条中线交于一点 B.三角形的三条高都在三角形内部
C.三角形不一定具有稳定性 D.三角形的角平分线可能在三角形的内部或外部
5.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=130°,则∠A的度数为( )
A.80° B.70° C.60° D.45°
6.如图,CD是△ABC的中线,点E和点F分别是CD和AE的中点,若△BEF的面积为,则△ABC的面积为( )
A.6 B.4 C.3 D.2
7.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接CE,BF,有下列说法:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=AE,其中,正确的说法有( )
A.②③ B.①③ C.①②③④ D.①②③
8.如图,在四边形ABCD中,AB∥CD,∠C=90°,E是BC上一点,AE、ED分别平分∠BAD、∠CDA,若AB=12,DC=4,则AD等于( )
A.12 B.16 C.18 D.20
9.如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N,CD与BM交于点E.下列结论:①∠ABM=∠ACD;②DM=DN;③∠AMD=45°;④S△EDN=S△ADM.其中正确结论有( )个.
A.1 B.2 C.3 D.4
10.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
二.填空题(共8小题)
11.如图,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2022与∠A2022CD的平分线相交于点A2023,得∠A2023,则∠A2023度数是 .
12.△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
13.在△ABC是AB=5,AC=3,BC边的中线AD的取值范围是 .
14.纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为 .
15.已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|+|c﹣a﹣b|= .
16.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
17.如图,在△ABC与△ADE中,E在BC边上,AD=AB,AE=AC,DE=BC,若∠1=25°,则∠DAB= °,∠2= °.
18.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①AD=BE;②∠AOB=70°;③△CPQ为等边三角形;④△APC≌△BQC.其中正确的有 .(注:把正确的答案序号都写上)
三.解答题(共10小题)
19.如图,点A,D,B,E在同一直线上,AD=BE,AC=DF,∠A=∠BDF,求证:BC∥EF.
20.如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:∠AEO=∠CFO.
21.如图,点A、B、C、D在一条直线上,点E、F分别在AD的两侧,连接AF、CF、BE、DE,BE∥CF,AB=CD,∠E=∠F.求证:BE=CF.
22.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
24.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,BE=4,求AB的长.
25.如图,点B、F、C、E在一条直线上,OA=OD,AC∥FD,AD交BE于O.
(1)求证:△ACO≌△DFO;
(2)若BF=CE.求证:AB∥DE.
26.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
27.如图,已知,AB=AC,点D、E分别在AC、AB上,且AE=AD,∠B=∠C,连接EC,BD、EC交BD于点M、连接AM.
(1)求证:△EBM≌△DCM;
(2)嘉琪说:“若S△BEM=S△ADM,则E是AB的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.
28.已知,△ABC中,CA=CB,∠ACB=90°,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.
(1)如图1,求证:EF=AE+BF;
(2)如图2,请直接写出EF,AE,BF之间的数量关系 ;
(3)在(2)的条件下,若BF=3AE,EF=4,求△BFC的面积.
参考答案
一.选择题(共10小题)
1.B.
2.D.
3.A.
4.A.
5.A.
6.A.
7.B.
8.B.
9.D.
10.B.
二.填空题(共8小题)
11.x°.
12.直角.
13.1<AD<4.
14.60°.
15.a+3b﹣c.
16.7.
17.25,25.
18.①③④.
三.解答题(共10小题)
19.如图,点A,D,B,E在同一直线上,AD=BE,AC=DF,∠A=∠BDF,求证:BC∥EF.
证明:∵点A,D,B,E在同一直线上,AD=BE,
∴AD+DB=BE+DB,
∴AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠ABC=∠E,
∴BC∥EF.
20.如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:∠AEO=∠CFO.
证明:∵BF=DE,
∴BF﹣EF=DE﹣EF,
即BE=DF,
在△ABE和△DFC中,
,
∴△ABE≌△CDF(SSS),
∴∠AEB=∠CFD,
∴∠AEO=∠CFO.
21.如图,点A、B、C、D在一条直线上,点E、F分别在AD的两侧,连接AF、CF、BE、DE,BE∥CF,AB=CD,∠E=∠F.求证:BE=CF.
证明:BE∥CF,
∴∠EBD=∠ACF,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB,
在△DBE和△ACF中,
,
∴△DBE≌△ACF(AAS),
∴BE=CF.
22.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.
证明:∵AC=BC,
∴∠A=∠B,
∵AC=BC BC=BD,
∴AC=BD,
∵∠CDB=∠A+∠ACD=∠CDE+∠BDE,∠CDE=∠A,
∴∠ACD=∠BDE,
在△ACD与△BDE中,
,
∴△ACD≌△BDE(ASA),
∴CD=DE.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
(1)证明:∵AB∥CD,
∴∠BAE=∠FCD,
∵AF=CE,
∴AE=CF,
又∵AB=CD,
∴△ABE≌△CDF(SAS).
(2)解:∵∠BCE=30°,∠CBE=70°,
∴∠AEB=∠BCE+∠CBE=30°+70°=100°,
∵△ABE≌△CDF,
∴∠CFD=∠AEB=100°.
24.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,BE=4,求AB的长.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵∠AED=∠AFD=90°,AD=AD,DE=DF,
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF,
∵AC=20,CF=BE=4,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
25.如图,点B、F、C、E在一条直线上,OA=OD,AC∥FD,AD交BE于O.
(1)求证:△ACO≌△DFO;
(2)若BF=CE.求证:AB∥DE.
证明:(1)∵AC∥FD,
∴∠CAO=∠FDO,
在△ACO与△DFO中
,
∴△ACO≌△DFO(AAS);
(2)∵△ACO≌△DFO,
∴OF=OC,
∵BF=CE,
∴BO=EO,
在△ABO与△DEO中
,
∴△ABO≌△DEO(SAS),
∴∠B=∠E,
∴AB∥DE.
26.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
解:∵∠AEB=90°,AD⊥DC,BC⊥DC,
∴∠AEB=∠ADE=∠BCE=90°,
∴∠AED+∠DAE=90°,∠AED+∠BEC=90°,∠BEC+∠EBC=90°,
∴∠DAE=∠CEB,∠AED=∠EBC,
又∵AE=BE,
∴△ADE≌△ECB(ASA),
∴AD=CE,DE=BC,
又∵AD=150米,BC=350米,
∴DC=DE+CE=BC+AD=350+150=500(米).
答:两个排污口之间的水平距离DC为500米.
27.如图,已知,AB=AC,点D、E分别在AC、AB上,且AE=AD,∠B=∠C,连接EC,BD、EC交BD于点M、连接AM.
(1)求证:△EBM≌△DCM;
(2)嘉琪说:“若S△BEM=S△ADM,则E是AB的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.
(1)证明:∵AB=AE+BE,AC=AD+CD,
又∵AB=AC,AE=AD,
∴BE=CD,
在△EBM和△DCM中,
,
∴△EBM≌△DCM(AAS)
(2)解:嘉琪的说法正确,理由如下:
∵△EBM≌△DCM,
∴ME=MD,
在△AEM和△ADM中,
,
∴△AEM≌△ADM(SSS),
S△AEM=S△ADM;
∵S△BEM=S△ADM,
∴S△BEM=S△AEM,
过点M作MF⊥AB于点F,
则,
∴AE=BE,
即E是AB的中点.
28.已知,△ABC中,CA=CB,∠ACB=90°,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.
(1)如图1,求证:EF=AE+BF;
(2)如图2,请直接写出EF,AE,BF之间的数量关系 EF=BF﹣AE ;
(3)在(2)的条件下,若BF=3AE,EF=4,求△BFC的面积.
(1)证明:∵∠ACB=90°,
∴∠ECA+∠FCB=90°,
又∵AE⊥EF,BF⊥EF,
∴∠AEF=∠BFC=90°,
∴∠ECA+∠EAC=90°,
∴∠FCB=∠EAC,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∵EF=EC+CF,
∴EF=AE+BF;
(2)解:EF=BF﹣AE,理由如下:
∵∠AEC=∠CFB=90°,∠ACB=90°,
∴∠ACE+∠CAE=∠ACE+∠BCF=90°,
∴∠CAE=∠BCF
又∵AC=BC,
∴△CAE≌△BCF(AAS),
∴CE=BF,AE=CF,
∴EF=CE﹣CF=BF﹣AE,
即EF=BF﹣AE;
故答案为:EF=BF﹣AE;
(3)解:由(2)得EF=AE+BF且BF=3AE,
∴CE=3AE,
∵CF=AE,
∴EF=2AE=4,
∴AE=CF=2,BF=6,
∴△BFC的面积=.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
