重庆市兼善中学2022-2023学年高二下学期第二次月考数学试卷(含解析)
文档属性
| 名称 | 重庆市兼善中学2022-2023学年高二下学期第二次月考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 658.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 21:34:54 | ||
图片预览




文档简介
重庆市兼善中学2022-2023学年高二下学期第二次月考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.命题:,的否定是( )
A., B.,
C., D.,
2.已知集合,,则( )
A. B. C. D.
3.已知a,b为实数,则使得“”成立的一个充分不必要条件为( )
A. B. C. D.
4.某班9名同学参加植树活动,若将9名同学分成挖土、植树、浇水3个小组,每组3人,则甲、乙、丙3人在不同小组的安排方法的种数为( )
A.90 B.180 C.540 D.3240
5.已知在7个电子元件中,有2个次品,5个合格品,每次任取一个测试,测试完后不再放回,直到2个次品都找到为止,则经过3次测试恰好将2个次品全部找出的概率为( )
A. B. C. D.
6.某中学的“信息”“足球”“摄影”三个社团考核挑选新社员,已知高一某新生对这三个社团都很感兴趣,决定三个考核都参加,假设他通过“信息”“足球”“摄影”三个社团考核的概率依次为,m,n,且他是否通过每个考核相互独立,若三个社团考核他都通过的概率为,至少通过一个社团考核的概率为,则( )
A. B. C. D.
7.的展开式中,的系数为( )
A.15 B.20 C.30 D.35
8.若函数恰有两个零点,则a的取值范围是( )
A. B. C. D.
二、多项选择题
9.已知某校高二男生的身高X(单位:cm)服从正态分布,且,则( )
A.该校高二男生的平均身高是175cm
B.该校高二男生身高的方差为4
C.该校高二男生中身高超过183cm的人数超过总数的3%
D.从该校高二男生中任选一人,身高超过180cm的概率与身高不超过170cm的概率相等
10.过点的直线与函数的图象相切于点,则的值可以是( )
A.0 B.2 C.3 D.
11.某市为了研究该市空气中的浓度和浓度之间的关系,环境监测部门对该市空气质量进行调研,随机抽查了100天空气中的浓度和浓度(单位:),得到如下所示的列联表:
64 16
10 10
则可以推断出( )
附:,其中.
0.10 0.05 0010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.该市一天空气中浓度不超过,且浓度不超过的概率估计值是0.64
B.若列联表中的天数都扩大到原来的10倍,的观测值不会发生变化
C.有超过99%的把握认为该市一天空气中浓度与浓度有关
D.在犯错的概率不超过1%的条件下,认为该市一天空气中浓度与浓度无关
12.有3台车床加工同一型号的零件,第1台加工的次品率为8%,第2台加工的次品率为3%,第3台加工的次品率为2%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的10%,40%,50%,从混放的零件中任取一个零件,则下列结论正确的是( )
A.该零件是第1台车床加工出来的次品的概率为0.08
B.该零件是次品的概率为0.03
C.如果该零件是第3台车床加工出来的,那么它不是次品的概率为0.98
D.如果该零件是次品,那么它不是第3台车床加工出来的概率为
三、填空题
13.函数在区间上的最大值是___________.
14.已知正数a、b,满足,则的最小值__________.
15.佛山被誉为“南国陶都”,拥有上千年的制陶史,佛山瓷砖享誉海内外.某企业瓷砖生产线上生产的瓷砖某项指标,且,现从该生产线上随机抽取10片瓷砖,记Y表示的瓷砖片数,则______.
16.甲、乙两队进行自由式轮滑速度障碍赛决赛,采取五场三胜制(当一队赢得三场比赛时,该队获胜,比赛结束),根据以往比赛成绩可知,甲队每场比赛获胜的概率为,比赛结果没有平局,且各场比赛结果相互独立,则在甲队获胜的情况下,比赛共进行了四场的概率为______.
四、解答题
17.近年来随着教育科研的不断进步,兼善中学教育质量不断提高,某知名机构对近年来升入北京航空航天大学兼善学子人数作了如下统计
年份 2018 2019 2020 2021 2022
时间代号t 1 2 3 4 5
人数y(人) 5 6 7 8 10
附:回归方程中,,.
(1)求y关于t的回归方程;
(2)用所求回归方程预测兼善中学2023年()升入北航的人数.
18.已知函数,.
(1)求函数的单调区间;
(2)若函数在上有两个不同的零点,求实数a的取值范围.
19.乡村民宿立足农村,契合了现代人远离喧嚣 亲近自然 寻味乡愁的美好追求.某镇在旅游旺季前夕,为了解各乡村的普通型民宿和品质型民宿的品质,随机抽取了8家规模较大的乡村民宿,统计得到各家的房间数如下表:
民宿点 甲 乙 丙 丁 戊 己 庚 辛
普通型民宿 16 8 12 14 13 18 9 20
品质型民宿 6 16 4 10 11 10 9 12
(1)从这8家中随机抽取3家,在抽取的这3家的普通型民宿的房间均不低于10间的条件下,求这3家的品质型民宿的房间均不低于10间的概率;
(2)从这8家中随机抽取4家,记X为抽取的这4家中普通型民宿的房间不低于15间的家数,求X的分布列和数学期望.
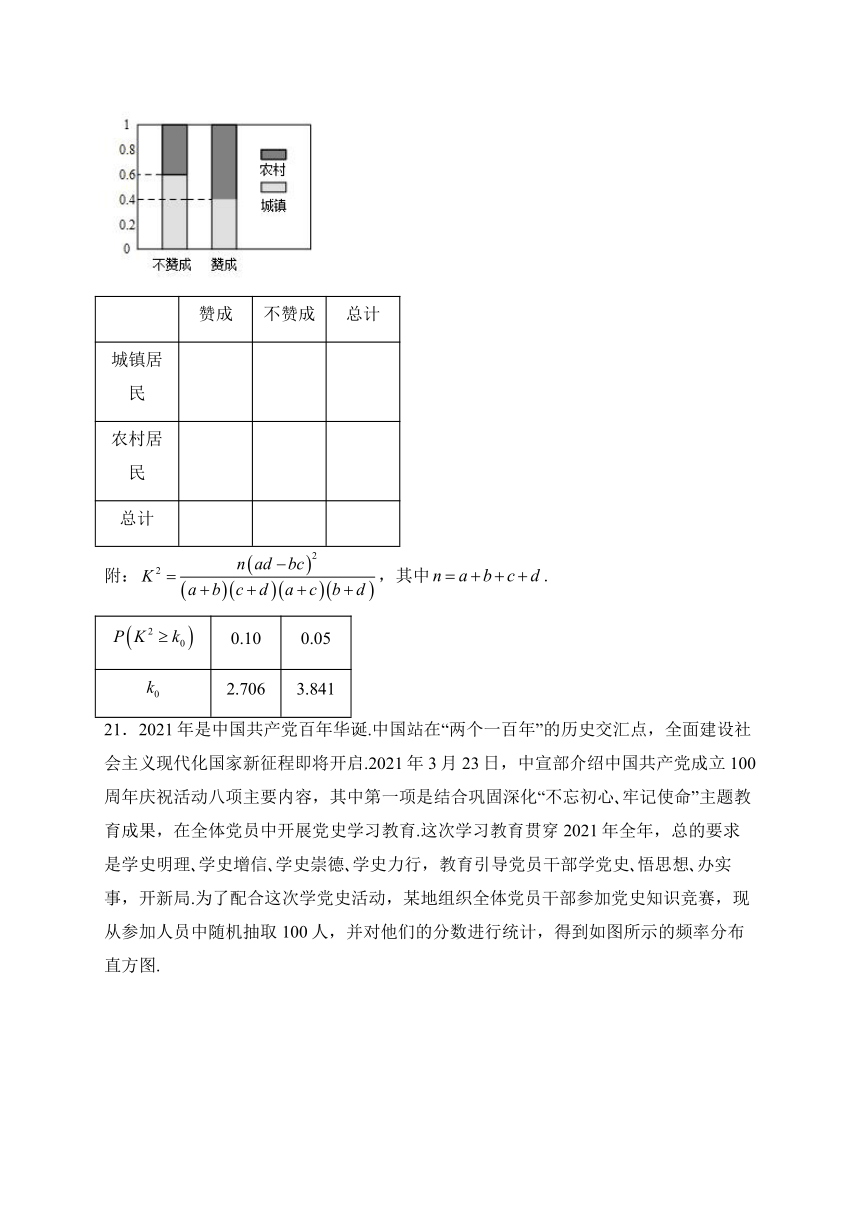
20.某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和3门学生自主选择的高中学业水平等级性考试科目成绩共同构成,该省教育厅为了解正在读高中的学生家长对高考改革方案所持的态度,随机从中抽取了100名城乡学生家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见,如图是根据样本的调查结果绘制的等高条形图.
(1)根据已知条件与等高条形图完成下面的列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口关”?
(2)用样本的频率估计概率,若随机在全省不赞成高考改革的家长中抽取3人,记这3个家长中是城镇户口的人数为X,试求X的分布列及数学期望.
赞成 不赞成 总计
城镇居民
农村居民
总计
附:,其中.
0.10 0.05
2.706 3.841
21.2021年是中国共产党百年华诞.中国站在“两个一百年”的历史交汇点,全面建设社会主义现代化国家新征程即将开启.2021年3月23日,中宣部介绍中国共产党成立100周年庆祝活动八项主要内容,其中第一项是结合巩固深化“不忘初心 牢记使命”主题教育成果,在全体党员中开展党史学习教育.这次学习教育贯穿2021年全年,总的要求是学史明理 学史增信 学史崇德 学史力行,教育引导党员干部学党史 悟思想 办实事,开新局.为了配合这次学党史活动,某地组织全体党员干部参加党史知识竞赛,现从参加人员中随机抽取100人,并对他们的分数进行统计,得到如图所示的频率分布直方图.
(1)现从这100人中随机抽取2人,记其中得分不低于80分的人数为,试求随机变量的分布列及期望;
(2)由频率分布直方图,可以认为该地参加党史知识竞赛人员的分数X服从正态分布,其中近似为样本平均数,近似为样本方差,经计算.现从所有参加党史知识竞赛的人员中随机抽取500人,且参加党史知识竞赛的人员的分数相互独立,试问这500名参赛者的分数不低于82.3的人数最有可能是多少?
参考数据:,,,.
22.已知函数的最大值为,的图像关于y轴对称.
(1)求实数a,b的值.
(2)设,则是否存在区间,使得函数在区间上的值域为?若存在,求实数k的取值范围;若不存在,请说明理由.
参考答案
1.答案:B
解析:命题:,的否定是,.
故选:B.
2.答案:D
解析:由题意可得:,,
所以.
故选:D.
3.答案:D
解析:对于A,如果,例如,,则,不能推出,如果,则必定有,既不是充分条件也不是必要条件,错误;
对于B,如果,根据对数函数的单调性可知,,但不能推出,例如,,不是充分条件,
如果,则,是必要条件,即是的必要不充分条件,错误;
对于C,如果,因为是单调递增的函数,所以,不能推出,例如,
如果,则必有,是必要不充分条件,错误;
对于D,如果,则必有,是充分条件,如果,例如,,则不能推出,所以是充分不必有条件,正确.
故选:D.
4.答案:C
解析:将除甲、乙、丙3人之外的6名同学分成挖土、植树、浇水3组,每组2人,有种不同的方法.
甲、乙、丙3人分到3个不同的小组,有种不同的方法.
由分步乘法计数原理知,共有种不同的安排方法.故选C.
5.答案:B
解析:从7个电子元件中选3个的排列数为,
经过3次测试恰好将2个次品全部找出,则第3次是次品,前2次中有一次是次品的排列数为,
经过3次测试恰好将2个次品全部找出为事件A,
则.
故选:B.
6.答案:B
解析:因至少通过一个社团考核的概率为,则三个社团都没有通过的概率为,依题意,
得即,解得.
故选:B.
7.答案:C
解析:,设其通项为,
要求的系数,只需求时,中的项即可.
设其通项为,显然时满足要求,
故的系数为.
故选:C.
8.答案:D
解析:当时,则无零点,不符合题意;
当时,令,则,
故原题意等价于与有两个交点,
构建,则,
令,解得;令,解得;
则在上单调递增,在上单调递减,
可得,且当x趋近于时,趋近于0,
所以的图象如图所示,由图象可得:
若与有两个交点,则,解得,
故a的取值范围是.
故选:D.
9.答案:AD
解析:对选项A:在中,为平均数,正确;
对选项B:方差为,错误;
对选项C:,则身高超过的概率,错误;
对选项D:正态曲线关于直线对称,所以身高超过180cm的概率与身高不超过170cm的概率相等,正确;
故选:AD.
10.答案:AD
解析:因为,所以,
由题意得直线的斜率,
即,解得或.
故选:AD.
11.答案:AC
解析:经计算,
对于A,该市一天空气中浓度不超过,且浓度不超过的概率估计值是,故A正确,
对于B,,故B错误,
对于C,,有超过99%的把握认为该市一天空气中浓度与浓度有关,故C正确,
在犯错的概率不超过1%的条件下,认为该市一天空气中浓度与浓度有关,故D错误.
故选:AC.
12.答案:BC
解析:记事件A:车床加工的零件为次品,记事件:第i台车床加工的零件,
则,,,,,,
对于A,任取一个零件是第1台生产出来的次品概率为,故A错误;
对于B,任取一个零件是次品的概率为,故B正确;
对于C,如果该零件是第3台车床加工出来的,那么它不是次品的概率为,故C正确;
对于D,如果该零件是次品,那么它不是第3台车床加工出来的概率为,故D错误.
故选:BC.
13.答案:2
解析:由题意可知,,
令,则或2,
所以在上单调递增,在上单调递减,且,,,
所以在上的最大值是2.
故答案为:2.
14.答案:
解析:,,
则,当且仅当时等号成立.
故答案为:.
15.答案:1
解析:因为,均值为,且,
所以,
由题可得,所以.
故答案为:1.
16.答案:/
解析:设事件A为“甲队最终获得胜利”,事件B为“比赛共进行了四场”,
①比赛进行三场,甲队均胜,;
②比赛进行四场,甲队前三场恰好胜二场,输一场,第四场胜,;
③比赛进行五场,甲队第五场胜,前四场恰好胜二场,输二场,,
则,,故所求概率为.
故答案为:.
17.答案:(1)
(2)11人
解析:(1)这里,,,
又,,
从而,.
故所求回归方程为.
(2)将代入回归方程(人).故升入北航11人.
18.答案:(1)单调递增区间为和,单调递减区间为
(2)
解析:(1)因为,所以,
所以当或时,当时,
所以的单调递增区间为和,单调递减区间为.
(2)由(1)可知在上单调递减,在上单调递增,
所以,又,,
因为函数在上有两个不同的零点,
所以,即,解得,即实数a的取值范围为.
19.答案:(1)
(2)
解析:(1)由题可知这8家乡村民宿中普通型民宿的房间不低于10间的有6家,品质型民宿和普通型民宿的房间均不低于10间的有4家.
记“这3家的普通型民宿的房间均不低于10间”为事件A,“这3家的品质型民宿的房间均不低于10间”为事件B,则,,
所以.
(2)这8家乡村民宿中普通型民宿的房间不低于15间的有3家,故X的所有可能取值为0,1,2,3.
,,
,,
所以X的分布列如下表:
X 0 1 2 3
P
所以.
20.答案:(1)表格见解析,没有95%的把握认为“赞成高考改革方案与城乡户口有关”
(2)分布列见解析,1.8
解析:(1)完成列联表,如下:
赞成 不赞成 总计
城镇居民 30 15 45
农村居民 45 10 55
总计 75 25 100
代入公式,得.
我们没有95%的把握认为“赞成高考改革方案与城乡户口有关”.
(2)用样本的频率估计概率,随机在全省不赞成高考改革的家长中抽中城镇户口家长的概率为0.6,抽中农村户口家长的概率为0.4.
X的可能取值为0,1,2,3,
;;
;.
的分布列为
X 0 1 2 3
P 0.064 0.288 0.432 0.216
.
21、
(1)答案:分布列答案见解析,数学期望:
解析:100人中得分不低于80分的人数为,
随机变量可能的取值为0,1,2.
又,,,
则的分布列为:
0 1 2
P
.
(2)答案:人数最有可能是79
解析:.
,
,
每位参赛者分数不低于82.3的概率为0.15865,记500位参赛者中分数不低于82.3的人数为随机变量,则,其中,
所以恰好有k个参赛者的分数不低于82.3的概率为,,1,2,…,500.
由,
得.
所以当时,,
当时,,
由此可知,在这500名参赛者中分数不低于82.3的人数最有可能是79.
22.答案:(1),
(2)不存在,理由见解析
解析:(1)依题意,,当时,,当时,,函数在上递增,在上递减,
则当时,,解得,
又的图像关于y轴对称,即,解得,
所以,.
(2)由(1)知,,即,,求导得,
令,,则,即在上单调递增,
则有,有函数在上单调递增,
假设存在区间,使得函数在区间上的值域是,
则有,于是得关于x的方程在内存在两个不相等的实根,
即方程在内存在两个不相等的实根,
令,,则,
设,,则,
即函数在上单调递增,于是得,即,
从而得函数在上单调递增,因此,方程在内不存在两个不相等的实根,
所以不存在区间,使得函数在区间上的值域是.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.命题:,的否定是( )
A., B.,
C., D.,
2.已知集合,,则( )
A. B. C. D.
3.已知a,b为实数,则使得“”成立的一个充分不必要条件为( )
A. B. C. D.
4.某班9名同学参加植树活动,若将9名同学分成挖土、植树、浇水3个小组,每组3人,则甲、乙、丙3人在不同小组的安排方法的种数为( )
A.90 B.180 C.540 D.3240
5.已知在7个电子元件中,有2个次品,5个合格品,每次任取一个测试,测试完后不再放回,直到2个次品都找到为止,则经过3次测试恰好将2个次品全部找出的概率为( )
A. B. C. D.
6.某中学的“信息”“足球”“摄影”三个社团考核挑选新社员,已知高一某新生对这三个社团都很感兴趣,决定三个考核都参加,假设他通过“信息”“足球”“摄影”三个社团考核的概率依次为,m,n,且他是否通过每个考核相互独立,若三个社团考核他都通过的概率为,至少通过一个社团考核的概率为,则( )
A. B. C. D.
7.的展开式中,的系数为( )
A.15 B.20 C.30 D.35
8.若函数恰有两个零点,则a的取值范围是( )
A. B. C. D.
二、多项选择题
9.已知某校高二男生的身高X(单位:cm)服从正态分布,且,则( )
A.该校高二男生的平均身高是175cm
B.该校高二男生身高的方差为4
C.该校高二男生中身高超过183cm的人数超过总数的3%
D.从该校高二男生中任选一人,身高超过180cm的概率与身高不超过170cm的概率相等
10.过点的直线与函数的图象相切于点,则的值可以是( )
A.0 B.2 C.3 D.
11.某市为了研究该市空气中的浓度和浓度之间的关系,环境监测部门对该市空气质量进行调研,随机抽查了100天空气中的浓度和浓度(单位:),得到如下所示的列联表:
64 16
10 10
则可以推断出( )
附:,其中.
0.10 0.05 0010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.该市一天空气中浓度不超过,且浓度不超过的概率估计值是0.64
B.若列联表中的天数都扩大到原来的10倍,的观测值不会发生变化
C.有超过99%的把握认为该市一天空气中浓度与浓度有关
D.在犯错的概率不超过1%的条件下,认为该市一天空气中浓度与浓度无关
12.有3台车床加工同一型号的零件,第1台加工的次品率为8%,第2台加工的次品率为3%,第3台加工的次品率为2%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的10%,40%,50%,从混放的零件中任取一个零件,则下列结论正确的是( )
A.该零件是第1台车床加工出来的次品的概率为0.08
B.该零件是次品的概率为0.03
C.如果该零件是第3台车床加工出来的,那么它不是次品的概率为0.98
D.如果该零件是次品,那么它不是第3台车床加工出来的概率为
三、填空题
13.函数在区间上的最大值是___________.
14.已知正数a、b,满足,则的最小值__________.
15.佛山被誉为“南国陶都”,拥有上千年的制陶史,佛山瓷砖享誉海内外.某企业瓷砖生产线上生产的瓷砖某项指标,且,现从该生产线上随机抽取10片瓷砖,记Y表示的瓷砖片数,则______.
16.甲、乙两队进行自由式轮滑速度障碍赛决赛,采取五场三胜制(当一队赢得三场比赛时,该队获胜,比赛结束),根据以往比赛成绩可知,甲队每场比赛获胜的概率为,比赛结果没有平局,且各场比赛结果相互独立,则在甲队获胜的情况下,比赛共进行了四场的概率为______.
四、解答题
17.近年来随着教育科研的不断进步,兼善中学教育质量不断提高,某知名机构对近年来升入北京航空航天大学兼善学子人数作了如下统计
年份 2018 2019 2020 2021 2022
时间代号t 1 2 3 4 5
人数y(人) 5 6 7 8 10
附:回归方程中,,.
(1)求y关于t的回归方程;
(2)用所求回归方程预测兼善中学2023年()升入北航的人数.
18.已知函数,.
(1)求函数的单调区间;
(2)若函数在上有两个不同的零点,求实数a的取值范围.
19.乡村民宿立足农村,契合了现代人远离喧嚣 亲近自然 寻味乡愁的美好追求.某镇在旅游旺季前夕,为了解各乡村的普通型民宿和品质型民宿的品质,随机抽取了8家规模较大的乡村民宿,统计得到各家的房间数如下表:
民宿点 甲 乙 丙 丁 戊 己 庚 辛
普通型民宿 16 8 12 14 13 18 9 20
品质型民宿 6 16 4 10 11 10 9 12
(1)从这8家中随机抽取3家,在抽取的这3家的普通型民宿的房间均不低于10间的条件下,求这3家的品质型民宿的房间均不低于10间的概率;
(2)从这8家中随机抽取4家,记X为抽取的这4家中普通型民宿的房间不低于15间的家数,求X的分布列和数学期望.
20.某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和3门学生自主选择的高中学业水平等级性考试科目成绩共同构成,该省教育厅为了解正在读高中的学生家长对高考改革方案所持的态度,随机从中抽取了100名城乡学生家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见,如图是根据样本的调查结果绘制的等高条形图.
(1)根据已知条件与等高条形图完成下面的列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口关”?
(2)用样本的频率估计概率,若随机在全省不赞成高考改革的家长中抽取3人,记这3个家长中是城镇户口的人数为X,试求X的分布列及数学期望.
赞成 不赞成 总计
城镇居民
农村居民
总计
附:,其中.
0.10 0.05
2.706 3.841
21.2021年是中国共产党百年华诞.中国站在“两个一百年”的历史交汇点,全面建设社会主义现代化国家新征程即将开启.2021年3月23日,中宣部介绍中国共产党成立100周年庆祝活动八项主要内容,其中第一项是结合巩固深化“不忘初心 牢记使命”主题教育成果,在全体党员中开展党史学习教育.这次学习教育贯穿2021年全年,总的要求是学史明理 学史增信 学史崇德 学史力行,教育引导党员干部学党史 悟思想 办实事,开新局.为了配合这次学党史活动,某地组织全体党员干部参加党史知识竞赛,现从参加人员中随机抽取100人,并对他们的分数进行统计,得到如图所示的频率分布直方图.
(1)现从这100人中随机抽取2人,记其中得分不低于80分的人数为,试求随机变量的分布列及期望;
(2)由频率分布直方图,可以认为该地参加党史知识竞赛人员的分数X服从正态分布,其中近似为样本平均数,近似为样本方差,经计算.现从所有参加党史知识竞赛的人员中随机抽取500人,且参加党史知识竞赛的人员的分数相互独立,试问这500名参赛者的分数不低于82.3的人数最有可能是多少?
参考数据:,,,.
22.已知函数的最大值为,的图像关于y轴对称.
(1)求实数a,b的值.
(2)设,则是否存在区间,使得函数在区间上的值域为?若存在,求实数k的取值范围;若不存在,请说明理由.
参考答案
1.答案:B
解析:命题:,的否定是,.
故选:B.
2.答案:D
解析:由题意可得:,,
所以.
故选:D.
3.答案:D
解析:对于A,如果,例如,,则,不能推出,如果,则必定有,既不是充分条件也不是必要条件,错误;
对于B,如果,根据对数函数的单调性可知,,但不能推出,例如,,不是充分条件,
如果,则,是必要条件,即是的必要不充分条件,错误;
对于C,如果,因为是单调递增的函数,所以,不能推出,例如,
如果,则必有,是必要不充分条件,错误;
对于D,如果,则必有,是充分条件,如果,例如,,则不能推出,所以是充分不必有条件,正确.
故选:D.
4.答案:C
解析:将除甲、乙、丙3人之外的6名同学分成挖土、植树、浇水3组,每组2人,有种不同的方法.
甲、乙、丙3人分到3个不同的小组,有种不同的方法.
由分步乘法计数原理知,共有种不同的安排方法.故选C.
5.答案:B
解析:从7个电子元件中选3个的排列数为,
经过3次测试恰好将2个次品全部找出,则第3次是次品,前2次中有一次是次品的排列数为,
经过3次测试恰好将2个次品全部找出为事件A,
则.
故选:B.
6.答案:B
解析:因至少通过一个社团考核的概率为,则三个社团都没有通过的概率为,依题意,
得即,解得.
故选:B.
7.答案:C
解析:,设其通项为,
要求的系数,只需求时,中的项即可.
设其通项为,显然时满足要求,
故的系数为.
故选:C.
8.答案:D
解析:当时,则无零点,不符合题意;
当时,令,则,
故原题意等价于与有两个交点,
构建,则,
令,解得;令,解得;
则在上单调递增,在上单调递减,
可得,且当x趋近于时,趋近于0,
所以的图象如图所示,由图象可得:
若与有两个交点,则,解得,
故a的取值范围是.
故选:D.
9.答案:AD
解析:对选项A:在中,为平均数,正确;
对选项B:方差为,错误;
对选项C:,则身高超过的概率,错误;
对选项D:正态曲线关于直线对称,所以身高超过180cm的概率与身高不超过170cm的概率相等,正确;
故选:AD.
10.答案:AD
解析:因为,所以,
由题意得直线的斜率,
即,解得或.
故选:AD.
11.答案:AC
解析:经计算,
对于A,该市一天空气中浓度不超过,且浓度不超过的概率估计值是,故A正确,
对于B,,故B错误,
对于C,,有超过99%的把握认为该市一天空气中浓度与浓度有关,故C正确,
在犯错的概率不超过1%的条件下,认为该市一天空气中浓度与浓度有关,故D错误.
故选:AC.
12.答案:BC
解析:记事件A:车床加工的零件为次品,记事件:第i台车床加工的零件,
则,,,,,,
对于A,任取一个零件是第1台生产出来的次品概率为,故A错误;
对于B,任取一个零件是次品的概率为,故B正确;
对于C,如果该零件是第3台车床加工出来的,那么它不是次品的概率为,故C正确;
对于D,如果该零件是次品,那么它不是第3台车床加工出来的概率为,故D错误.
故选:BC.
13.答案:2
解析:由题意可知,,
令,则或2,
所以在上单调递增,在上单调递减,且,,,
所以在上的最大值是2.
故答案为:2.
14.答案:
解析:,,
则,当且仅当时等号成立.
故答案为:.
15.答案:1
解析:因为,均值为,且,
所以,
由题可得,所以.
故答案为:1.
16.答案:/
解析:设事件A为“甲队最终获得胜利”,事件B为“比赛共进行了四场”,
①比赛进行三场,甲队均胜,;
②比赛进行四场,甲队前三场恰好胜二场,输一场,第四场胜,;
③比赛进行五场,甲队第五场胜,前四场恰好胜二场,输二场,,
则,,故所求概率为.
故答案为:.
17.答案:(1)
(2)11人
解析:(1)这里,,,
又,,
从而,.
故所求回归方程为.
(2)将代入回归方程(人).故升入北航11人.
18.答案:(1)单调递增区间为和,单调递减区间为
(2)
解析:(1)因为,所以,
所以当或时,当时,
所以的单调递增区间为和,单调递减区间为.
(2)由(1)可知在上单调递减,在上单调递增,
所以,又,,
因为函数在上有两个不同的零点,
所以,即,解得,即实数a的取值范围为.
19.答案:(1)
(2)
解析:(1)由题可知这8家乡村民宿中普通型民宿的房间不低于10间的有6家,品质型民宿和普通型民宿的房间均不低于10间的有4家.
记“这3家的普通型民宿的房间均不低于10间”为事件A,“这3家的品质型民宿的房间均不低于10间”为事件B,则,,
所以.
(2)这8家乡村民宿中普通型民宿的房间不低于15间的有3家,故X的所有可能取值为0,1,2,3.
,,
,,
所以X的分布列如下表:
X 0 1 2 3
P
所以.
20.答案:(1)表格见解析,没有95%的把握认为“赞成高考改革方案与城乡户口有关”
(2)分布列见解析,1.8
解析:(1)完成列联表,如下:
赞成 不赞成 总计
城镇居民 30 15 45
农村居民 45 10 55
总计 75 25 100
代入公式,得.
我们没有95%的把握认为“赞成高考改革方案与城乡户口有关”.
(2)用样本的频率估计概率,随机在全省不赞成高考改革的家长中抽中城镇户口家长的概率为0.6,抽中农村户口家长的概率为0.4.
X的可能取值为0,1,2,3,
;;
;.
的分布列为
X 0 1 2 3
P 0.064 0.288 0.432 0.216
.
21、
(1)答案:分布列答案见解析,数学期望:
解析:100人中得分不低于80分的人数为,
随机变量可能的取值为0,1,2.
又,,,
则的分布列为:
0 1 2
P
.
(2)答案:人数最有可能是79
解析:.
,
,
每位参赛者分数不低于82.3的概率为0.15865,记500位参赛者中分数不低于82.3的人数为随机变量,则,其中,
所以恰好有k个参赛者的分数不低于82.3的概率为,,1,2,…,500.
由,
得.
所以当时,,
当时,,
由此可知,在这500名参赛者中分数不低于82.3的人数最有可能是79.
22.答案:(1),
(2)不存在,理由见解析
解析:(1)依题意,,当时,,当时,,函数在上递增,在上递减,
则当时,,解得,
又的图像关于y轴对称,即,解得,
所以,.
(2)由(1)知,,即,,求导得,
令,,则,即在上单调递增,
则有,有函数在上单调递增,
假设存在区间,使得函数在区间上的值域是,
则有,于是得关于x的方程在内存在两个不相等的实根,
即方程在内存在两个不相等的实根,
令,,则,
设,,则,
即函数在上单调递增,于是得,即,
从而得函数在上单调递增,因此,方程在内不存在两个不相等的实根,
所以不存在区间,使得函数在区间上的值域是.
同课章节目录
