7.2.4 图形的运动教学课件(共33张PPT)六年级数学下册同步高效课堂系列 苏教版
文档属性
| 名称 | 7.2.4 图形的运动教学课件(共33张PPT)六年级数学下册同步高效课堂系列 苏教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 10:49:01 | ||
图片预览







文档简介
(共33张PPT)
小学数学·六年级(下)·SJ
第4课时 图形的运动
总复习 2.图形与几何
2.通过不同的图形,让学生从不同的角度来描述图形的变换方式,沟通知识间的联系与区别。
1.使学生进一步巩固对轴对称图形、图形的平移、旋转,放大与缩小的认识,并会画一个图形的轴对称图形。掌握图形运动的常用方法。
3.通过欣赏图形变换所创造出的美,进一步感觉对称、平移、旋转、放大与缩小在现实生活中的广泛应用,体会数学的文化价值,感受数学的美。
进一步掌握平移、旋转、轴对称、放大与缩小的特征。
掌握图形运动的常用方法,并能按要求画出图形,根据图形运动来解决实际生活问题。
在观察、操作、想象、设计图案等活动中, 发展空间观念。
整理与反思
Sort out and reflect
图形的运动有哪些情况呢?
平移
旋转
轴对称
图形的运动
放大与缩小
平移与旋转
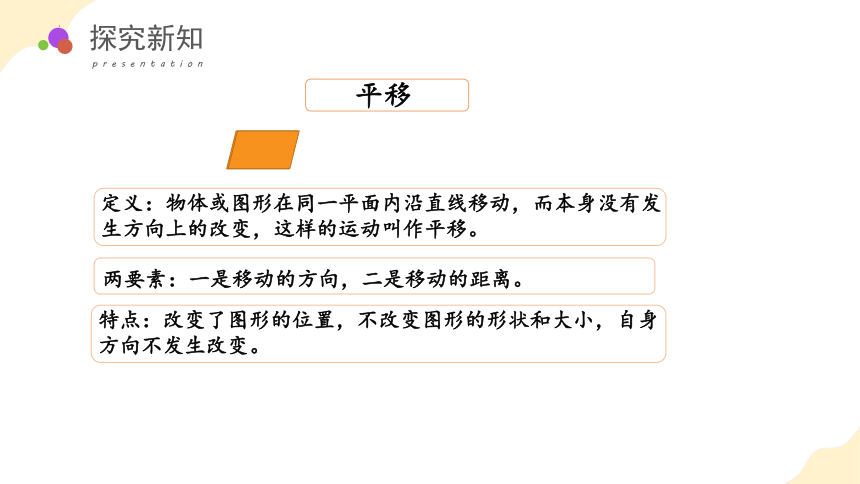
平移
定义:物体或图形在同一平面内沿直线移动,而本身没有发生方向上的改变,这样的运动叫作平移。
两要素:一是移动的方向,二是移动的距离。
特点:改变了图形的位置,不改变图形的形状和大小,自身方向不发生改变。
平移的距离
蜡烛向右平移了 格。
小鱼向 平移了 格。
4
5
左
在观察一个图形平移时,
要注意把对应点找正确。
对应点移动了几格,
图形就移动了几格。
·
·
·
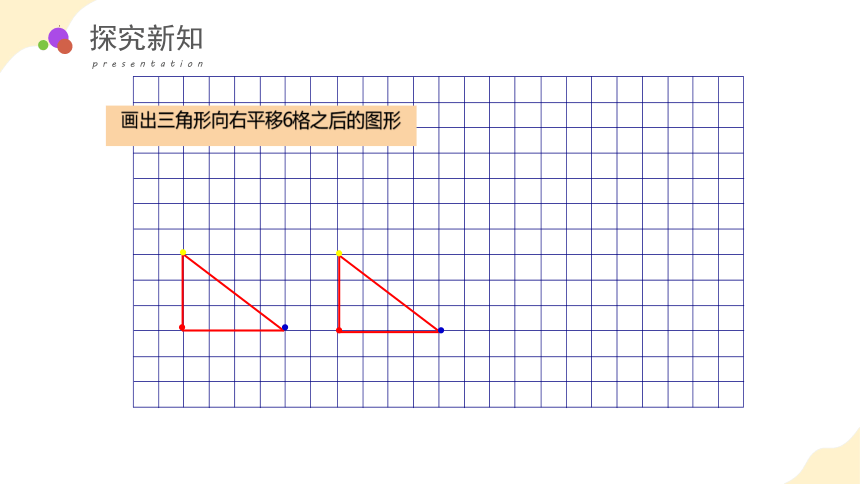
画出三角形向右平移6格之后的图形
·
·
·
平移图形的画法
选点:在原图形上选择几个能决定图形形状和大小的点,如三角形的三个顶点。
移点:按要求把选择的点向规定的方向移动规定的格数。
连点:对照原图形连接新移的点,使它与原图形完全相同。
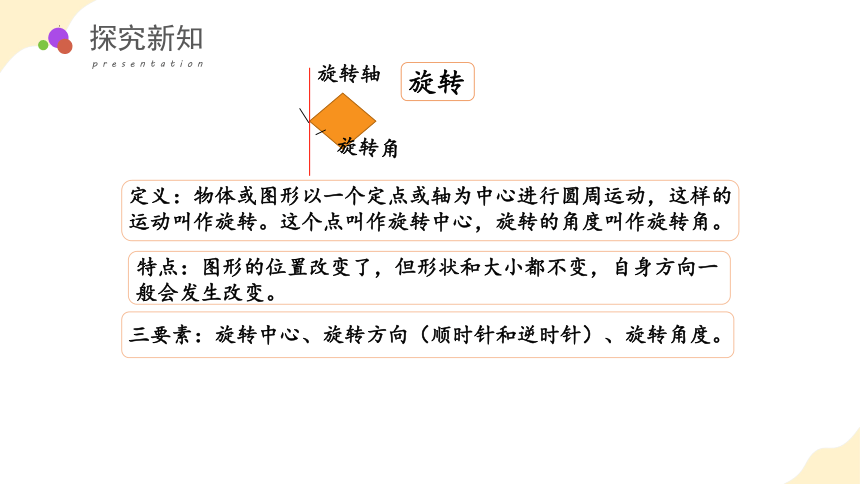
三要素:旋转中心、旋转方向(顺时针和逆时针)、旋转角度。
定义:物体或图形以一个定点或轴为中心进行圆周运动,这样的运动叫作旋转。这个点叫作旋转中心,旋转的角度叫作旋转角。
旋转
特点:图形的位置改变了,但形状和大小都不变,自身方向一般会发生改变。
旋转角
旋转轴
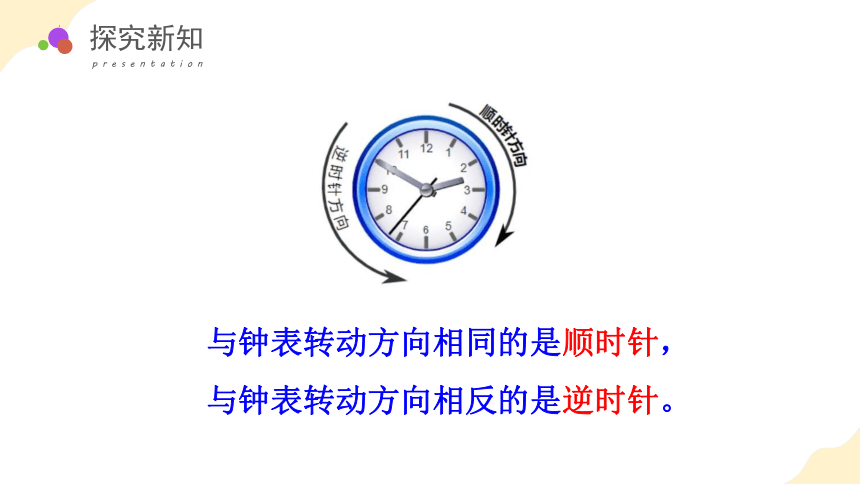
与钟表转动方向相同的是顺时针,
与钟表转动方向相反的是逆时针。
请将图形A绕点O 顺时针旋转90°,得到图形B,说说要注意什么。
O
A
B
旋转图形的画法
定点:确定旋转的中心。
定向:根据要求确定是按顺时针方向旋转,还是按逆时针方向旋转。
定度数:确定所要旋转的度数。
把组成的图形的每条线段按要求画出旋转后的位置,旋转后所有线段组成的图形即旋转后的图形。
C
把图C绕O点,逆时针旋转900
O
轴对称和缩放
特点:不改变图形的形状和大小。
定义:如果一个图形沿着一条直线对折,直线两侧
的部分能够完全重合,那么这个图形就叫作轴对称
图形,折痕所在的直线叫作对称轴。
轴对称图形
对称轴
常见轴对称图形的对称轴数量
对称图形 等腰三角形 等边三角形 长方形 菱形 等腰梯形 正方形 圆
对称轴
1条
3条
2条
2条
1条
4 条
无数条
画出图A的另一半,使它成为一个轴对称图形。
A
定义:把一个图形的各边按一定的比放大或缩小,可以得到该图形的放大图或缩小图。
特点:将一个图形进行放大或缩小之后,图形的大小变了,但形状没有变。
图形的放大与缩小
放大
缩小
把图A按1:2缩小,画出缩小后的图形B
A
把小平行四边形按3:1放大,画出放大后的图形
在按一定的比放大或缩小图形时,要牢记每条边都要放大或缩小相同的倍数。
变换 变换前后的图形比较 形状变化 大小变化
轴对称 改变 不改变
平移 不改变 不改变
旋转 不改变 不改变
放大与缩小 不改变 改变
解决实际问题
1.涂色小船向左平移4格后,得到的是小船( )。
B
2. 绕点E逆时针旋转90°后是( )。
B
A.
B.
C.
D.
3.拉抽屉的运动是( )现象;用钥匙开锁的运动是( )现象。
平移
旋转
4.观察下图,回答问题。
(1)当摩天轮转动使得小东转到最下面时,( )在最上面。(2)如果摩天轮旋转半圈,那么小军就到了现在( )的位置上。
小文
小光
梯形面积:
(2+5)×2÷2=7×2÷2=14÷2=7(平方厘米)
5.(2022.江苏镇江.毕业)下图中每个小方格的边长为1厘米。
(1)三角形面积是梯形面积的几分之几?(请用算式或其他方式写出思考过程)
三角形面积: 6×2÷2=12÷2=6(平方厘米)
答:三角形面积是梯形面积的
【分析】由图可知,三角形的底是6厘米,高是2厘米,梯形的上底是2厘米,下底是5厘米,高是2厘米,根据三角形面积和梯形的面积公式 ,可求出三角形和梯形的面积。再用三角形面积除以梯形面积即可求出三角形面积是梯形面积的几分之几。
6÷7=
5.(2022.江苏镇江.毕业)下图中每个小方格的边长为1厘米。
(2)如果图①不动,图②以每秒1厘米的速度向左平移,当图②平移第7秒时,与图①重叠部分的面积是多少平方厘米?
1×7=7(格)
重叠部分面积:
4×2÷2
=8÷2
=4(平方厘米) 答:重叠部分的面积是4平方厘米。
根据“路程=速度×时间”,可知图②向左移动了7格,与图①重叠的部分是个底是4厘米,高是2厘米的三角形,如下图,根据“三角形面积=底×高÷2”即可求出面积。
6.(2022.江苏无锡.毕业)在下面方格图中画一个直角三角形,其中两个顶点的位置分别是A(4,8)和B(2,5)。(每个方格边长1cm)
(1)第三个顶点C的位置是(4, )。(2)画出这个三角形绕点C顺时针旋转90°后的图形。(3)将图中三角形ABC按2∶1的比例放大后画在合适的位置,放大后的三角形面积与原来三角形的面积比是( )。
5
A
B
C
原来三角形的面积:
2×3÷2=3(平方厘米)
放大后三角形的面积:
4×6÷2=12(平方厘米)
所以放大后的三角形面积∶原来三角形的面积=12∶3=4∶1
4∶1
通过本节课的学习,你有了哪些新的收获呢?
1.平移、旋转、轴对称、缩放的基本特征。
2.掌握了图形运动后的图像画法。
1. 掌握图形运动的类型及相关特点,会画出图形运动后的图像。
2. 完成《分层作业》
小学数学·六年级(下)·SJ
第4课时 图形的运动
总复习 2.图形与几何
2.通过不同的图形,让学生从不同的角度来描述图形的变换方式,沟通知识间的联系与区别。
1.使学生进一步巩固对轴对称图形、图形的平移、旋转,放大与缩小的认识,并会画一个图形的轴对称图形。掌握图形运动的常用方法。
3.通过欣赏图形变换所创造出的美,进一步感觉对称、平移、旋转、放大与缩小在现实生活中的广泛应用,体会数学的文化价值,感受数学的美。
进一步掌握平移、旋转、轴对称、放大与缩小的特征。
掌握图形运动的常用方法,并能按要求画出图形,根据图形运动来解决实际生活问题。
在观察、操作、想象、设计图案等活动中, 发展空间观念。
整理与反思
Sort out and reflect
图形的运动有哪些情况呢?
平移
旋转
轴对称
图形的运动
放大与缩小
平移与旋转
平移
定义:物体或图形在同一平面内沿直线移动,而本身没有发生方向上的改变,这样的运动叫作平移。
两要素:一是移动的方向,二是移动的距离。
特点:改变了图形的位置,不改变图形的形状和大小,自身方向不发生改变。
平移的距离
蜡烛向右平移了 格。
小鱼向 平移了 格。
4
5
左
在观察一个图形平移时,
要注意把对应点找正确。
对应点移动了几格,
图形就移动了几格。
·
·
·
画出三角形向右平移6格之后的图形
·
·
·
平移图形的画法
选点:在原图形上选择几个能决定图形形状和大小的点,如三角形的三个顶点。
移点:按要求把选择的点向规定的方向移动规定的格数。
连点:对照原图形连接新移的点,使它与原图形完全相同。
三要素:旋转中心、旋转方向(顺时针和逆时针)、旋转角度。
定义:物体或图形以一个定点或轴为中心进行圆周运动,这样的运动叫作旋转。这个点叫作旋转中心,旋转的角度叫作旋转角。
旋转
特点:图形的位置改变了,但形状和大小都不变,自身方向一般会发生改变。
旋转角
旋转轴
与钟表转动方向相同的是顺时针,
与钟表转动方向相反的是逆时针。
请将图形A绕点O 顺时针旋转90°,得到图形B,说说要注意什么。
O
A
B
旋转图形的画法
定点:确定旋转的中心。
定向:根据要求确定是按顺时针方向旋转,还是按逆时针方向旋转。
定度数:确定所要旋转的度数。
把组成的图形的每条线段按要求画出旋转后的位置,旋转后所有线段组成的图形即旋转后的图形。
C
把图C绕O点,逆时针旋转900
O
轴对称和缩放
特点:不改变图形的形状和大小。
定义:如果一个图形沿着一条直线对折,直线两侧
的部分能够完全重合,那么这个图形就叫作轴对称
图形,折痕所在的直线叫作对称轴。
轴对称图形
对称轴
常见轴对称图形的对称轴数量
对称图形 等腰三角形 等边三角形 长方形 菱形 等腰梯形 正方形 圆
对称轴
1条
3条
2条
2条
1条
4 条
无数条
画出图A的另一半,使它成为一个轴对称图形。
A
定义:把一个图形的各边按一定的比放大或缩小,可以得到该图形的放大图或缩小图。
特点:将一个图形进行放大或缩小之后,图形的大小变了,但形状没有变。
图形的放大与缩小
放大
缩小
把图A按1:2缩小,画出缩小后的图形B
A
把小平行四边形按3:1放大,画出放大后的图形
在按一定的比放大或缩小图形时,要牢记每条边都要放大或缩小相同的倍数。
变换 变换前后的图形比较 形状变化 大小变化
轴对称 改变 不改变
平移 不改变 不改变
旋转 不改变 不改变
放大与缩小 不改变 改变
解决实际问题
1.涂色小船向左平移4格后,得到的是小船( )。
B
2. 绕点E逆时针旋转90°后是( )。
B
A.
B.
C.
D.
3.拉抽屉的运动是( )现象;用钥匙开锁的运动是( )现象。
平移
旋转
4.观察下图,回答问题。
(1)当摩天轮转动使得小东转到最下面时,( )在最上面。(2)如果摩天轮旋转半圈,那么小军就到了现在( )的位置上。
小文
小光
梯形面积:
(2+5)×2÷2=7×2÷2=14÷2=7(平方厘米)
5.(2022.江苏镇江.毕业)下图中每个小方格的边长为1厘米。
(1)三角形面积是梯形面积的几分之几?(请用算式或其他方式写出思考过程)
三角形面积: 6×2÷2=12÷2=6(平方厘米)
答:三角形面积是梯形面积的
【分析】由图可知,三角形的底是6厘米,高是2厘米,梯形的上底是2厘米,下底是5厘米,高是2厘米,根据三角形面积和梯形的面积公式 ,可求出三角形和梯形的面积。再用三角形面积除以梯形面积即可求出三角形面积是梯形面积的几分之几。
6÷7=
5.(2022.江苏镇江.毕业)下图中每个小方格的边长为1厘米。
(2)如果图①不动,图②以每秒1厘米的速度向左平移,当图②平移第7秒时,与图①重叠部分的面积是多少平方厘米?
1×7=7(格)
重叠部分面积:
4×2÷2
=8÷2
=4(平方厘米) 答:重叠部分的面积是4平方厘米。
根据“路程=速度×时间”,可知图②向左移动了7格,与图①重叠的部分是个底是4厘米,高是2厘米的三角形,如下图,根据“三角形面积=底×高÷2”即可求出面积。
6.(2022.江苏无锡.毕业)在下面方格图中画一个直角三角形,其中两个顶点的位置分别是A(4,8)和B(2,5)。(每个方格边长1cm)
(1)第三个顶点C的位置是(4, )。(2)画出这个三角形绕点C顺时针旋转90°后的图形。(3)将图中三角形ABC按2∶1的比例放大后画在合适的位置,放大后的三角形面积与原来三角形的面积比是( )。
5
A
B
C
原来三角形的面积:
2×3÷2=3(平方厘米)
放大后三角形的面积:
4×6÷2=12(平方厘米)
所以放大后的三角形面积∶原来三角形的面积=12∶3=4∶1
4∶1
通过本节课的学习,你有了哪些新的收获呢?
1.平移、旋转、轴对称、缩放的基本特征。
2.掌握了图形运动后的图像画法。
1. 掌握图形运动的类型及相关特点,会画出图形运动后的图像。
2. 完成《分层作业》
