八年级数学下册试题 第二十三章 《概率初步》单元测试卷 -沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第二十三章 《概率初步》单元测试卷 -沪教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 00:00:00 | ||
图片预览




文档简介
第二十三章 《概率初步》单元测试卷
一、选择题(每小题4分,共24分)
1.若气象部门预报明天下雨的概率是70%,下列说法正确的是( )
A.明天下雨的可能性比较大 B.明天一定不会下雨
C.明天一定会下雨 D.明天下雨的可能性比较小
2.在一个不透明的袋子里有1个红球,2个蓝球和2个白球,这些球除颜色外都相同,从中随机摸出一个球,恰好是白球的概率是( )
A. B. C. D.
3.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.则此口袋中估计白球的个数是( )个.
A.20 B.30 C.40 D.50
4.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
5.“无偿献血,让你我血脉相连”,会宁县某中学有5名教师自愿献血,其中3人血型为O型,2人血型为A型,现从他们当中随机挑选2人参与献血,抽到的两人均为O型血的概率为( )
A. B. C. D.
6.一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A. B. C. D.
二、填空题(每小题4分,共48分)
7.在一个不透明的袋子里装有4个白球,若干个黄球,每个球除颜色外均相同,将球搅匀,从中任意摸出一个球,摸到黄球的概率为,则袋子内共有球 个.
8.一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 .
9.一个不透明的口袋中装有3个红球和5个黄球,它们除颜色外,其他都相同,往口袋中再放入x个红球和y个黄球,若从口袋中随机摸出一个红球的概率是,则y与x之间的函数表达式是 .
10.有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②矩形;③平行四边形;④圆;⑤菱形,将卡片背面朝上洗匀,从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是 .
11.如图,BP平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形△ABC内有一点M,则点M落在△BPC内(包括边界)的概率为 .
12.如果小球在图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是 .
13.技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 .(结果要求保留两位小数)
14.从数﹣1、、0、2中任取一个数记为a,再从余下的三个数中任取一个数记为b,若k=a+b,则k<0的概率是 .
15.2020年某校将迎来70周年校庆,学校安排3位男老师和2位女老师一起筹办大型文艺晚会,并随机地从中抽取2位老师主持晚会,则最后确定的主持人是一男一女的概率为 .
16.经过某T字路口的行人,可能左拐,也可能右拐.假设这两种可能性相同.现有两人经过该路口,则恰好有一人右拐,另一人左拐的概率为 .
17.将一枚六个面编号分别为1、2、3、4、5、6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x、y的方程组只有正数解的概率为 .
18.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
三、解答题(共78分)
19.在一个不透明的盒子中装有三张卡片,分别标有数字1,2,5,这些卡片除数字不同外其余均相同,现从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为偶数的概率.
20.某人制成了一个如图所示的游戏转盘,转盘被分成8个相同的扇形,取名为“开心转转转”.游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则参与者交费2元;若指针指向字母“B”,则参与者获奖3元,若指针指向字母“C”,则参与者获奖1元.那么任意转动转盘一次,转盘停止后,参与者交费2元、参与者获奖3元、参与者获奖1元的概率各为多少?
21.在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了.请判断以下事情是不确定事件、不可能事件,还是必然事件.
(1)从口袋中任意取出一个球,是一个白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了.
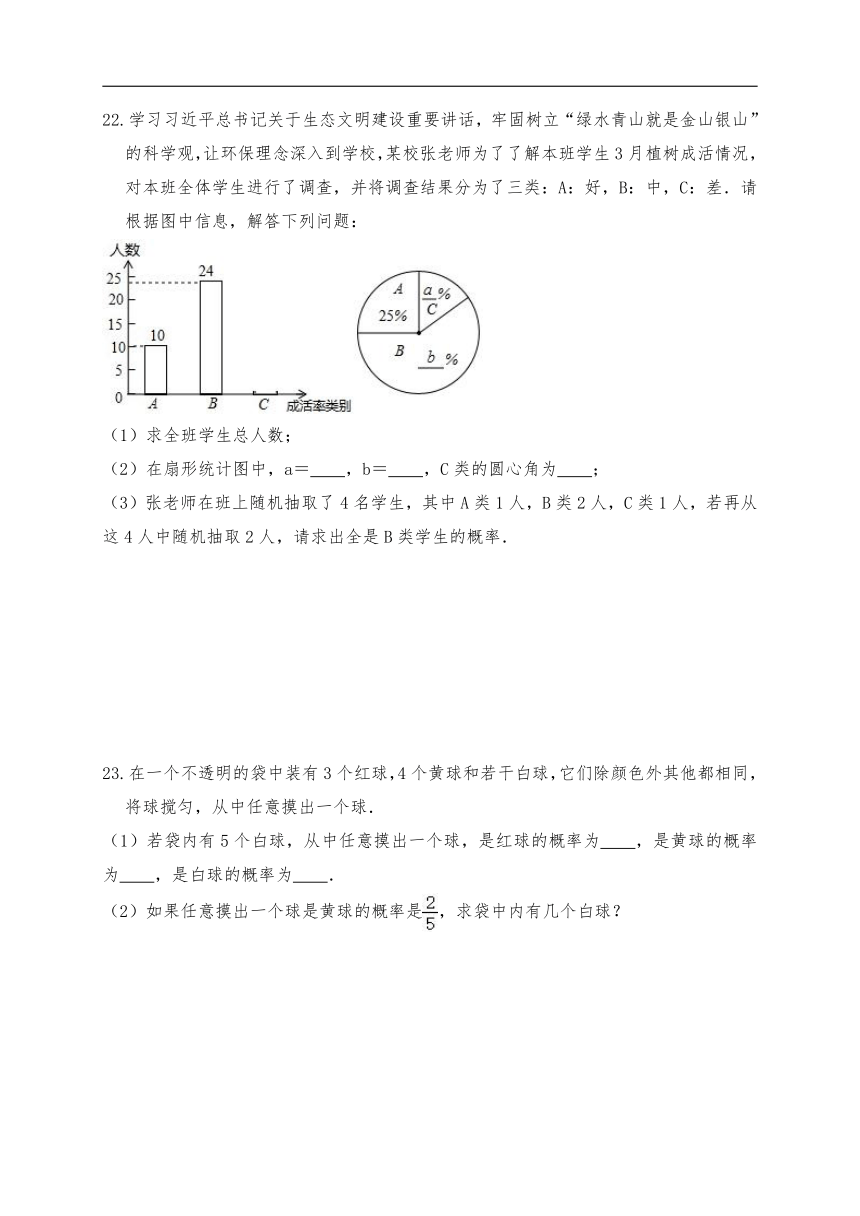
22.学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= ,b= ,C类的圆心角为 ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.
23.在一个不透明的袋中装有3个红球,4个黄球和若干白球,它们除颜色外其他都相同,将球搅匀,从中任意摸出一个球.
(1)若袋内有5个白球,从中任意摸出一个球,是红球的概率为 ,是黄球的概率为 ,是白球的概率为 .
(2)如果任意摸出一个球是黄球的概率是,求袋中内有几个白球?
24.有A、B两组卡片,卡片上除数字外完全相同,A组有三张,分别标有数字1、2、﹣3.B组有二张,分别标有数字﹣1、2.小明闭眼从A组中随机抽出一张,记录其标有的数字为x,再从B组中随机抽出一张,记录其标有的数字为y,这样就确定点P的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点P的所有可能坐标;
(2)求点P落在第一象限的概率.
25.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 290 480 601
摸到白球的频率 0.64 0.58 0.60 0.601
(1)完成上表;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
答案
一、选择题
1.A
【分析】根据“概率”的意义进行判断即可.
【解答】解:A. 明天下雨的概率是70%,即明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项A符合题意,
B. 明天下雨的可能性比较大,与明天一定不会下雨是矛盾的,因此选项B不符合题意;
C. 明天下雨的可能性是70%,并不代表明天一定会下雨,因此选项C不符合题意;
D. 明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项D不符合题意,
故选:A.
2.C
【分析】根据概率的意义求解即可.
【解答】解:共有5个球,其中白球有2个,占,
所以随机摸出一个球,恰好是白球的概率为,
故选:C.
3.B
【分析】要先根据红球的频率列方程,再解答即可.
【解答】解:设口袋中有x个白球,
由题意,得10:(10+x)=50:200;
解得:x=30.
把x=30代入10+x得,10+30=40≠0,故x=30是原方程的解.
答:口袋中约有30个白球.
故选:B.
4.B
【分析】根据大量的试验结果稳定在0.82左右即可得出结论.
【解答】解:∵从频率的波动情况可以发现频率稳定在0.82附近,
∴这名运动员射击一次时“射中九环以上”的概率是0.82.
故选:B.
5.A
【分析】根据题意画出树状图得出所有等可能的结果,找出符合条件的情况数,再根据概率公式即可得出答案.
【解答】解:画树状图如下:
∵共有20种等可能的结果,其中抽到的两人均为O型血的结果有6种,
∴抽到的两人均为O型血的概率为=.
故选:A.
6.A
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与满足关于x的方程x2+px+q=0有实数根的情况,继而利用概率公式即可求得答案.
【解答】解:画树状图得:
∵x2+px+q=0有实数根,
∴△=b2﹣4ac=p2﹣4q≥0,
∵共有6种等可能的结果,满足关于x的方程x2+px+q=0有实数根的有(1,﹣1),(2,﹣1),(2,1)共3种情况,
∴满足关于x的方程x2+px+q=0有实数根的概率是:=.
故选:A.
二、填空题
7.20
【分析】设袋子内共有球x个,利用概率公式得到=,然后利用比例性质求出x即可.
【解答】解:设袋子内共有球x个,
根据题意得=,
解得x=20,
经检验x=20为原方程的解,
即袋子内共有球20个.
故答案为20.
8.6
【分析】根据概率的意义列方程求解即可.
【解答】解:由题意得,
=,
解得,n=6,
经检验,n=6是原方程的解,
所以原方程的解为n=6,
故答案为:6.
9.y=3x+4
【分析】用红球的数量除以球的总个数得出=,化简可得答案.
【解答】解:根据题意,得:=,
整理,得:y=3x+4,
故答案为:y=3x+4.
10.解:①线段;②矩形;③平行四边形;④圆;⑤菱形中,既是轴对称图形,又是中心对称图形是①②④⑤共4个,
故从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是:.
故答案为:.
11.
【分析】据已知条件证得△ABP≌△EBP,根据全等三角形的性质得到AP=PE,得出S△ABP=S△EBP,S△ACP=S△ECP,推出S△PBC=S△ABC,根据概率公式可得的答案.
【解答】解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC,
则点M落在△BPC内(包括边界)的概率=.
故答案为.
12.
【分析】直接利用概率公式计算得出答案.
【解答】解:∵由图可知,共有16块方砖,其中黑色方砖6块,
∴黑色方砖在整个地板中所占的比值=,
故答案为:.
13.0.99
【分析】根据抽检某一产品2020件,发现产品合格的频率已达到0.9911,所以估计合格件数的概率为0.99,问题得解.
【解答】解:∵抽检某一产品2020件,发现产品合格的频率已达到0.9911,
∴依此我们可以估计该产品合格的概率为0.99,
故答案为:0.99.
14.【分析】画树状图列出所有等可能结果,再从中找到使a、b两数的和小于0的结果数,根据概率公式计算可得.
【解答】解:画树状图如下:
由树状图知共有12种等可能结果,其中能使a、b两数的和小于0的有4种结果,
∴k<0的概率是=,
故答案为:.
15.【分析】根据题意画出树状图得出所有等可能的情况数,再找出符合条件的情况数,然后根据概率公式即可得出答案.
【解答】解:根据题意画图如下:
共有20种等可能的情况数,其中最后确定的主持人是一男一女的有12种,
则最后确定的主持人是一男一女的概率为=.
故答案为:.
16.【分析】画出树状图,共有4个等可能的结果,则恰好有一人右拐,另一人左拐的结果有2个,由概率公式求解即可.
【解答】解:画树状图如图:
共有4个等可能的结果,则恰好有一人右拐,另一人左拐的结果有2个,
∴两人经过该路口,则恰好有一人右拐,另一人左拐的概率为=;
故答案为:.
17.【分析】首先分两种情况:①当a﹣2b=0时,方程组无解;
②当a﹣2b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.把方程组两式联合求解可得x=,y=,再由x、y都大于0可得x=>0,y=>0,求出a、b的范围,列举出a,b所有的可能结果,然后求出有正数解时,所有的可能,进而求出概率.
【解答】解:当a﹣2b=0时,方程组无解;
②当a﹣2b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.
易知a,b都为大于0的整数,则两式联合求解可得x=,y=,
∵使x、y都大于0则有x=>0,y=>0,
∴解得a<,b>或者a>,b<,
∵a,b都为1到6的整数,
∴可知当a为1时b只能是1,2,3,4,5,6;或者a为2,3,4,5,6时b无解,
这两种情况的总出现可能有6种;
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6),
又掷两次骰子出现的基本事件共6×6=36种情况,故所求概率为==;
故答案为:.
18.【分析】依据选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,可得能拼成一个正方形的概率为.
【解答】解:由题可得,随机选取两位同学,可能的结果如下:
甲乙、甲丙、乙丙,
∵a2+2ab+b2=(a+b)2,
∴选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,
∴能拼成一个正方形的概率为,
故答案为:.
三、解答题
19.解:画树状图为:
共有9种等可能的结果数,其中两次抽取的卡片上数字之和为偶数的结果数为5,
所以两次抽取的卡片上数字之和为偶数的概率=.
20.解:任意转动转盘一次,转盘停止后,参与者交费2元的概率==;
参与者获奖3元的概率=;
参与者获奖1元的概率=.
21.解:(1)从口袋中任意取出一个球,可能是一个白球、一个红球也可能是一个蓝球,
∴从口袋中任意取出一个球,是一个白球是随机事件,即不确定事件;
(2)口袋中只有3个蓝球,
∴从口袋中一次任取5个球,全是蓝球是不可能事件;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了是必然事件.
22.解:(1)全班学生总人数为:10÷25%=40(人);
(2)∵C类人数为:40﹣(10+24)=6(人),
∴C类所占百分比为×100%=15%,C类的圆心角为360°×=54°,B类百分比为×100%=60%,
∴a=15,b=60,54°;
故答案为:a=15,b=60,54°;
(3)列表如下:
A B B C
A BA BA CA
B AB BB CB
B AB BB CB
C AC BC BC
由表可知,共有12种等可能结果,其中全是B类学生的有2种结果,
∴全是B类学生的概率为=.
23.解:(1)从中任意摸出一个球,是红球的概率==,是黄球的概率==,是白球的概率==;
(2)设袋中内有x个白球,
根据题意得=,
解得x=3,
即袋中内有3个白球.
故答案为;;.
24.解:(1)画树状图为:
共有6种等可能的结果数,它们是(1,﹣1),(1,2),(2,﹣1),(2,2),(﹣3,﹣1),(﹣3,2);
(2)P点在第一象限的结果为2,
所以点P落在第一象限的概率==.
25.解:(1)填表如下:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 290 480 601
摸到白球的频率 0.59 0.64 0.58 0.58 0.60 0.601
(2)“摸到白球”的概率的估计值是0.60;
(3)由(2)摸到白球的概率为0.60,所以可估计口袋中白种颜色的球的个数=20×0.6=12(个),黑球20﹣12=8(个).
答:黑球8个,白球12个.
故答案为:(1)0.59,0.58;(2)0.6.
一、选择题(每小题4分,共24分)
1.若气象部门预报明天下雨的概率是70%,下列说法正确的是( )
A.明天下雨的可能性比较大 B.明天一定不会下雨
C.明天一定会下雨 D.明天下雨的可能性比较小
2.在一个不透明的袋子里有1个红球,2个蓝球和2个白球,这些球除颜色外都相同,从中随机摸出一个球,恰好是白球的概率是( )
A. B. C. D.
3.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.则此口袋中估计白球的个数是( )个.
A.20 B.30 C.40 D.50
4.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
5.“无偿献血,让你我血脉相连”,会宁县某中学有5名教师自愿献血,其中3人血型为O型,2人血型为A型,现从他们当中随机挑选2人参与献血,抽到的两人均为O型血的概率为( )
A. B. C. D.
6.一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A. B. C. D.
二、填空题(每小题4分,共48分)
7.在一个不透明的袋子里装有4个白球,若干个黄球,每个球除颜色外均相同,将球搅匀,从中任意摸出一个球,摸到黄球的概率为,则袋子内共有球 个.
8.一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 .
9.一个不透明的口袋中装有3个红球和5个黄球,它们除颜色外,其他都相同,往口袋中再放入x个红球和y个黄球,若从口袋中随机摸出一个红球的概率是,则y与x之间的函数表达式是 .
10.有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②矩形;③平行四边形;④圆;⑤菱形,将卡片背面朝上洗匀,从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是 .
11.如图,BP平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形△ABC内有一点M,则点M落在△BPC内(包括边界)的概率为 .
12.如果小球在图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是 .
13.技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 .(结果要求保留两位小数)
14.从数﹣1、、0、2中任取一个数记为a,再从余下的三个数中任取一个数记为b,若k=a+b,则k<0的概率是 .
15.2020年某校将迎来70周年校庆,学校安排3位男老师和2位女老师一起筹办大型文艺晚会,并随机地从中抽取2位老师主持晚会,则最后确定的主持人是一男一女的概率为 .
16.经过某T字路口的行人,可能左拐,也可能右拐.假设这两种可能性相同.现有两人经过该路口,则恰好有一人右拐,另一人左拐的概率为 .
17.将一枚六个面编号分别为1、2、3、4、5、6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x、y的方程组只有正数解的概率为 .
18.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
三、解答题(共78分)
19.在一个不透明的盒子中装有三张卡片,分别标有数字1,2,5,这些卡片除数字不同外其余均相同,现从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为偶数的概率.
20.某人制成了一个如图所示的游戏转盘,转盘被分成8个相同的扇形,取名为“开心转转转”.游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则参与者交费2元;若指针指向字母“B”,则参与者获奖3元,若指针指向字母“C”,则参与者获奖1元.那么任意转动转盘一次,转盘停止后,参与者交费2元、参与者获奖3元、参与者获奖1元的概率各为多少?
21.在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了.请判断以下事情是不确定事件、不可能事件,还是必然事件.
(1)从口袋中任意取出一个球,是一个白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了.
22.学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= ,b= ,C类的圆心角为 ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.
23.在一个不透明的袋中装有3个红球,4个黄球和若干白球,它们除颜色外其他都相同,将球搅匀,从中任意摸出一个球.
(1)若袋内有5个白球,从中任意摸出一个球,是红球的概率为 ,是黄球的概率为 ,是白球的概率为 .
(2)如果任意摸出一个球是黄球的概率是,求袋中内有几个白球?
24.有A、B两组卡片,卡片上除数字外完全相同,A组有三张,分别标有数字1、2、﹣3.B组有二张,分别标有数字﹣1、2.小明闭眼从A组中随机抽出一张,记录其标有的数字为x,再从B组中随机抽出一张,记录其标有的数字为y,这样就确定点P的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点P的所有可能坐标;
(2)求点P落在第一象限的概率.
25.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 290 480 601
摸到白球的频率 0.64 0.58 0.60 0.601
(1)完成上表;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
答案
一、选择题
1.A
【分析】根据“概率”的意义进行判断即可.
【解答】解:A. 明天下雨的概率是70%,即明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项A符合题意,
B. 明天下雨的可能性比较大,与明天一定不会下雨是矛盾的,因此选项B不符合题意;
C. 明天下雨的可能性是70%,并不代表明天一定会下雨,因此选项C不符合题意;
D. 明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项D不符合题意,
故选:A.
2.C
【分析】根据概率的意义求解即可.
【解答】解:共有5个球,其中白球有2个,占,
所以随机摸出一个球,恰好是白球的概率为,
故选:C.
3.B
【分析】要先根据红球的频率列方程,再解答即可.
【解答】解:设口袋中有x个白球,
由题意,得10:(10+x)=50:200;
解得:x=30.
把x=30代入10+x得,10+30=40≠0,故x=30是原方程的解.
答:口袋中约有30个白球.
故选:B.
4.B
【分析】根据大量的试验结果稳定在0.82左右即可得出结论.
【解答】解:∵从频率的波动情况可以发现频率稳定在0.82附近,
∴这名运动员射击一次时“射中九环以上”的概率是0.82.
故选:B.
5.A
【分析】根据题意画出树状图得出所有等可能的结果,找出符合条件的情况数,再根据概率公式即可得出答案.
【解答】解:画树状图如下:
∵共有20种等可能的结果,其中抽到的两人均为O型血的结果有6种,
∴抽到的两人均为O型血的概率为=.
故选:A.
6.A
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与满足关于x的方程x2+px+q=0有实数根的情况,继而利用概率公式即可求得答案.
【解答】解:画树状图得:
∵x2+px+q=0有实数根,
∴△=b2﹣4ac=p2﹣4q≥0,
∵共有6种等可能的结果,满足关于x的方程x2+px+q=0有实数根的有(1,﹣1),(2,﹣1),(2,1)共3种情况,
∴满足关于x的方程x2+px+q=0有实数根的概率是:=.
故选:A.
二、填空题
7.20
【分析】设袋子内共有球x个,利用概率公式得到=,然后利用比例性质求出x即可.
【解答】解:设袋子内共有球x个,
根据题意得=,
解得x=20,
经检验x=20为原方程的解,
即袋子内共有球20个.
故答案为20.
8.6
【分析】根据概率的意义列方程求解即可.
【解答】解:由题意得,
=,
解得,n=6,
经检验,n=6是原方程的解,
所以原方程的解为n=6,
故答案为:6.
9.y=3x+4
【分析】用红球的数量除以球的总个数得出=,化简可得答案.
【解答】解:根据题意,得:=,
整理,得:y=3x+4,
故答案为:y=3x+4.
10.解:①线段;②矩形;③平行四边形;④圆;⑤菱形中,既是轴对称图形,又是中心对称图形是①②④⑤共4个,
故从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是:.
故答案为:.
11.
【分析】据已知条件证得△ABP≌△EBP,根据全等三角形的性质得到AP=PE,得出S△ABP=S△EBP,S△ACP=S△ECP,推出S△PBC=S△ABC,根据概率公式可得的答案.
【解答】解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC,
则点M落在△BPC内(包括边界)的概率=.
故答案为.
12.
【分析】直接利用概率公式计算得出答案.
【解答】解:∵由图可知,共有16块方砖,其中黑色方砖6块,
∴黑色方砖在整个地板中所占的比值=,
故答案为:.
13.0.99
【分析】根据抽检某一产品2020件,发现产品合格的频率已达到0.9911,所以估计合格件数的概率为0.99,问题得解.
【解答】解:∵抽检某一产品2020件,发现产品合格的频率已达到0.9911,
∴依此我们可以估计该产品合格的概率为0.99,
故答案为:0.99.
14.【分析】画树状图列出所有等可能结果,再从中找到使a、b两数的和小于0的结果数,根据概率公式计算可得.
【解答】解:画树状图如下:
由树状图知共有12种等可能结果,其中能使a、b两数的和小于0的有4种结果,
∴k<0的概率是=,
故答案为:.
15.【分析】根据题意画出树状图得出所有等可能的情况数,再找出符合条件的情况数,然后根据概率公式即可得出答案.
【解答】解:根据题意画图如下:
共有20种等可能的情况数,其中最后确定的主持人是一男一女的有12种,
则最后确定的主持人是一男一女的概率为=.
故答案为:.
16.【分析】画出树状图,共有4个等可能的结果,则恰好有一人右拐,另一人左拐的结果有2个,由概率公式求解即可.
【解答】解:画树状图如图:
共有4个等可能的结果,则恰好有一人右拐,另一人左拐的结果有2个,
∴两人经过该路口,则恰好有一人右拐,另一人左拐的概率为=;
故答案为:.
17.【分析】首先分两种情况:①当a﹣2b=0时,方程组无解;
②当a﹣2b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.把方程组两式联合求解可得x=,y=,再由x、y都大于0可得x=>0,y=>0,求出a、b的范围,列举出a,b所有的可能结果,然后求出有正数解时,所有的可能,进而求出概率.
【解答】解:当a﹣2b=0时,方程组无解;
②当a﹣2b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.
易知a,b都为大于0的整数,则两式联合求解可得x=,y=,
∵使x、y都大于0则有x=>0,y=>0,
∴解得a<,b>或者a>,b<,
∵a,b都为1到6的整数,
∴可知当a为1时b只能是1,2,3,4,5,6;或者a为2,3,4,5,6时b无解,
这两种情况的总出现可能有6种;
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6),
又掷两次骰子出现的基本事件共6×6=36种情况,故所求概率为==;
故答案为:.
18.【分析】依据选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,可得能拼成一个正方形的概率为.
【解答】解:由题可得,随机选取两位同学,可能的结果如下:
甲乙、甲丙、乙丙,
∵a2+2ab+b2=(a+b)2,
∴选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,
∴能拼成一个正方形的概率为,
故答案为:.
三、解答题
19.解:画树状图为:
共有9种等可能的结果数,其中两次抽取的卡片上数字之和为偶数的结果数为5,
所以两次抽取的卡片上数字之和为偶数的概率=.
20.解:任意转动转盘一次,转盘停止后,参与者交费2元的概率==;
参与者获奖3元的概率=;
参与者获奖1元的概率=.
21.解:(1)从口袋中任意取出一个球,可能是一个白球、一个红球也可能是一个蓝球,
∴从口袋中任意取出一个球,是一个白球是随机事件,即不确定事件;
(2)口袋中只有3个蓝球,
∴从口袋中一次任取5个球,全是蓝球是不可能事件;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了是必然事件.
22.解:(1)全班学生总人数为:10÷25%=40(人);
(2)∵C类人数为:40﹣(10+24)=6(人),
∴C类所占百分比为×100%=15%,C类的圆心角为360°×=54°,B类百分比为×100%=60%,
∴a=15,b=60,54°;
故答案为:a=15,b=60,54°;
(3)列表如下:
A B B C
A BA BA CA
B AB BB CB
B AB BB CB
C AC BC BC
由表可知,共有12种等可能结果,其中全是B类学生的有2种结果,
∴全是B类学生的概率为=.
23.解:(1)从中任意摸出一个球,是红球的概率==,是黄球的概率==,是白球的概率==;
(2)设袋中内有x个白球,
根据题意得=,
解得x=3,
即袋中内有3个白球.
故答案为;;.
24.解:(1)画树状图为:
共有6种等可能的结果数,它们是(1,﹣1),(1,2),(2,﹣1),(2,2),(﹣3,﹣1),(﹣3,2);
(2)P点在第一象限的结果为2,
所以点P落在第一象限的概率==.
25.解:(1)填表如下:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 290 480 601
摸到白球的频率 0.59 0.64 0.58 0.58 0.60 0.601
(2)“摸到白球”的概率的估计值是0.60;
(3)由(2)摸到白球的概率为0.60,所以可估计口袋中白种颜色的球的个数=20×0.6=12(个),黑球20﹣12=8(个).
答:黑球8个,白球12个.
故答案为:(1)0.59,0.58;(2)0.6.
