物理人教版(2019)必修第二册8.4机械能守恒定律(共28张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.4机械能守恒定律(共28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-11 07:12:18 | ||
图片预览







文档简介
(共28张PPT)
第八章 机械能守恒定律
第4节 机械能守恒定律
一、机械能
二、机械能守恒定律
第4节 机械能守恒定律
三、系统机械能守恒定律
新课引入
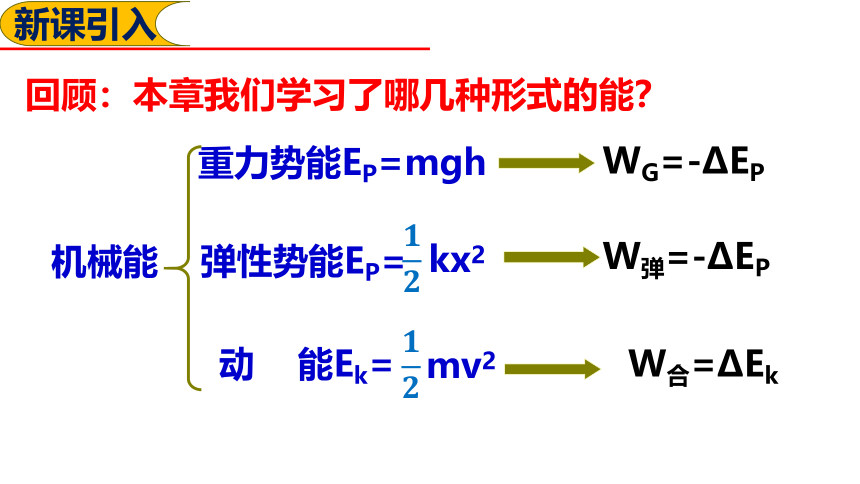
回顾:本章我们学习了哪几种形式的能?
重力势能EP=mgh
动 能Ek=
弹性势能EP=
W合=ΔEk
WG=-ΔEP
W弹=-ΔEP
机械能
kx2
mv2
一、机械能(mechanical energy)
1.概 念:
动能、重力势能和弹性势能的统称
2.表达式:
3.单 位:
焦耳(J)
4.标示性:
标量,具有相对性
E=Ek+EP
思考1:理想斜面实验小球总能回到原来高度说明什么
运动过程中有能保持不变的量
往下跑:动能和重力势能怎么变化?
EP减小、EK增加
往上跑:动能和重力势能怎么变化?
EP增加、EK减小
猜想:运动过程中小球EK和EP在相互转化,
但EK+EP
不变
h1
h2
V1
V2
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
参考平面
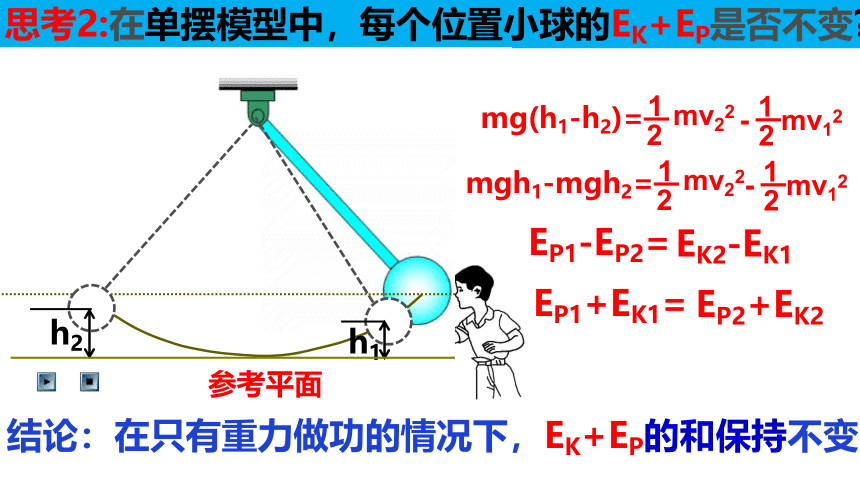
思考2:在单摆模型中,每个位置小球的EK+EP是否不变
参考平面
h1
h2
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
结论:在只有重力做功的情况下,EK+EP的和保持不变。
h1
h2
V1
V2
V0
结论:在只有重力做功的情况下,EK+EP的和保持不变
思考3:在各种抛体运动中,小球的EK+EP是否守恒
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
EK和EP发生互相转化,
二、机械能守恒定律
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
【典例1】若忽略空气阻力的影响,下列运动过程中物体机械能守恒的是( )
A.被掷出后在空中运动的铅球
B.沿粗糙斜面减速下滑的木块
C.随热气球一起匀速上升的吊篮
D.随倾斜传送带加速上行的货物
A
【典例2】荡秋千是一种常见的娱乐休闲活动(如图)。若秋千绳的长度l=2 m,荡到最高点时秋千绳与竖直方向的夹角θ=60°。取重力加速度g=9.8 m/s2,求荡到最低点时秋千的速度大小 (忽略阻力及秋千绳的质量,且人在秋千上的姿势可视为不变)
解:由机械能守恒:EP1+EK1=EP2+EK2
选择最低位置时的水平面为参考平面
mg(l-lcosθ)+
0=
0+
1
2
mv2
得v=
2gl(1-cosθ)
法2: 由机械能守恒EP1-EP2=EK2-EK1
mg(l-lcosθ)=
1
2
mv2-0
得v=
2gl(1-cosθ)
=
法3: 由动能定理WG=EK2-EK1
mg(l-lcosθ)=
1
2
mv2-0
得v=
=
【变式拓展】在现实中,若人在荡秋千时姿势不变,秋千将逐渐停下来,这是有阻力的缘故。因此,人荡秋千时,只有在保持姿势不变且忽略阻力的情况下,其机械能才守恒。为什么有的人可以越荡越高,他是怎么做到的呢?请分析原因。
人荡秋千时越荡越高,是在荡秋千的过程中,人通过做一些合适的动作做功,将人体内的化学能转化为人和秋千的机械能的缘故。
思考:人匀速楼梯,人的机械能是否守恒?
EK和EP发生互相转化,
二、机械能守恒定律
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
注意:
(1)可以受其它力,
但其它力不做功或做功代数和为零。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
(2)因涉及重力势能,所以此定律针对物体
和地球这个系统。
若其它力做了功,
则W非G=ΔE
二、机械能守恒定律
4.应用步骤:
①选对象,受力分析,做功分析。
②定减小的能和增加的能。
③列机守方程求解。
EK和EP发生互相转化,
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
【典例3】如图所示,两质量相同的小球A、B,分别用长度不同的线悬挂在等高的O1、O2点,A球的悬线比B球的悬线长。把两球的悬线均拉到水平后将小球无初速释放,以悬点为零势能参考面,不计空气阻力。两球经过最低点时,悬线上的拉力分别为FA、FB,所具有的机械能分别为EA和EB。则( )
A.FA=FB、EA=EB
B.FA>FB、EA>EB
C.FA=FB、EA>EB
D.FA>FB、EA=EB
A
思考1:绳拴两物体,在B下落过程中A的E机守恒吗?
结论:A的机械能在增加,ΔE=
WT
思考:由A、B构成的系统机械能守恒吗?
A、B构成的系统机械能守恒。
不计一切阻力
不计一切阻力
思考2:杆连两物体,在转动过程中A球的E机守恒吗?
结论:A的机械能不守恒,ΔE=
W杆
A、B构成的系统机械能守恒。
FN
S
FN
S/
思考:由A、B构成的系统机械能守恒吗?
思考3:直接连接的两物体,在运动过程中E机守恒吗?
结论:单个物体不守恒,但系统机械能守恒
不计一切阻力
不计一切阻力
结论:在只有弹簧弹力做功的情况下,小球的动能和
弹簧的弹性势能每个位置EK+EP的和保持不变。
思考4:小球在和弹簧作用的系统,小球机械能守恒吗?
W弹=
1
2
- mv12
1
2
mv22
W弹=
EP1-EP2
EP1-EP2=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
光滑水平面
原长
F弹
V1
V2
弹簧:
EP1+EK1=
EP2+EK2
思考:小球和弹簧这个系统机械能守恒吗?
结论:小球E不守恒
v0
A
B
A
B
Ff
Ff
l1
l2
Δl
思考5:系统内力中的摩擦力做功对系统的机械能是否影响
A对B做的功WAB=______
B对A做的功WBA=______
Ffl1
-Ffl2
结论:一对内力Ff对系统做负功。导致系统E减小
WAB+WBA=___________
Ffl1-Ffl2
=-FfΔl
VB
VA
-0
1
2
= mBvB2
1
2
- mAv02
1
2
= mAvA2
1
2
= mBvB2
1
2
- mAv02
1
2
+ mAvA2
光滑水平面
FfΔl=
1
2
mAv02
-
1
2
( mBvB2
1
2
+ mAvA2)
=EK初-EK末
三、系统机械能守恒定律
1.内容:
一个系统,若只有系统内力中的弹力做功,
2.表达式:
或
3.成立条件:
只有弹力做功。
注意:
(1)绳、杆、接触弹力对两物体做功抵消,
使E在两物体之间转移,系统E守恒。
每个物体机械能不守恒,但总机械能守恒。
E减=
E增
EP1+EK1=
EP2+EK2
(2)簧弹力对两端物体做功不能抵消,
使E在物体和弹簧间转移。包括弹簧的系统E守恒
(3)Ff对两物体做功不能抵消,
FfΔl==EK初-EK末
【典例4】一轻质理想弹簧一端固定在竖直墙壁上,一端固定在小木块上,如图所示,水平面光滑,用手推动小木块压缩弹簧一段后松手,在小木块反弹过中,下列说法正确的是( )
A.小木块机械能守恒
B.弹簧机械能守恒
C.小木块弹簧构成的系统机械能守恒
D.小木块弹簧构成的系统机械能不守恒
C
原长
F弹
【典例5】如下图所示,小球从高处下落到竖直放置的轻弹簧上,在从释放到将弹簧压缩到最短的整个过程中,下列关于能量的叙述中正确的是( )
A.小球的机械能不守恒,其机械能一直在增加
B.小球的动能先增大后减小,在刚接触弹簧时最大
C.小球和弹簧构成的系统机械能不守恒
D.重力势能、弹性势能和动能之和总保持不变
D
【典例6】如图所示实例中均不考虑空气阻力,系统机械能守恒的是( )
D
【典例7】如图所示,杂技演员在一根弹性绳上表演。位置a、b是弹性绳的两个固定端,ab连线位置是弹性绳的自然状态。演员从某一高度下落,到了ab连线位置之后,与弹性绳一起向下运动,位置c是演员和弹性绳运动的最低点。演员可视为质点,不考虑人的生物能转化,不计弹性绳的质量和空气阻力,则演员从ab连线位置运动到c点的过程中( )
A.演员的机械能保持不变
B.演员的动能不断减小
C.演员的机械能转化为弹性绳的弹性势能
D.演员的重力势能转化为演员的动能
C
【典例8】(多选)A、B两个物体通过一条轻绳跨过定滑轮相连,A的质量大于B的质量,不计各部分的摩擦阻力,如图所示,则释放后下列说法正确的是( )
A. B物体机械能减小
B. A物体机械能增加
C. A、B两物体机械能都不守恒
D. A、B构成的系统机械能守恒
CD
mBg
T
mAg
T
【典例9】(多选)如图所示,在质量分别为m和2m的小球a和b之间,用一根轻质细杆连接,两小球可绕过轻杆中心的水平轴无摩擦转动,现让轻杆处于水平位置,静止释放小球后,重球b向下转动,轻球a向上转动,在转过90°的过程中,以下说法正确的是( )
A.杆对a球不做功
B.杆对a球做负功
C.杆对b球做负功
D.a、b两球总机械能守恒
CD
b
a
0
【典例10】(多选)斜面A置于光滑的水平面上,滑块B置于A上由静止滑下,它们接触面光滑,如图所示,则下列说法正确的是( )
A. A物体机械能守恒
B. B物体机械能守恒
C. A、B两物体机械能都不守恒
D. A、B系统物体机械能守恒
CD
A
A
B
B
FN
G
S
FN
S、
【典例11】一光滑水平面上放着一个静止的木块,其质量为M,一个质量为m的子弹,以初速度v0射入木块,并最终留在木块内一起做匀速运动,则下列说法正确的是( )
A.小木块机械能守恒
B.木板机械能守恒
C.小木块、木板构成的系统机械能守恒
D.小木块、木板构成的系统机械能不守恒
D
v0
v共
S木
S子
摩擦力对子弹做的功W=
f
f
-f
S子
摩擦力对木块做的功W/=
f
S木
两者的功不能抵消
所以系统机械能不守恒
【典例12】一条长为L的均匀链条,放在光滑水平桌面上,链条的一半垂于桌边,如图所示?现由静止开始使链条自由滑落,当它全部脱离桌面时的速度为多大
解:设链条总质量为m
得:
+
-0
第八章 机械能守恒定律
第4节 机械能守恒定律
一、机械能
二、机械能守恒定律
第4节 机械能守恒定律
三、系统机械能守恒定律
新课引入
回顾:本章我们学习了哪几种形式的能?
重力势能EP=mgh
动 能Ek=
弹性势能EP=
W合=ΔEk
WG=-ΔEP
W弹=-ΔEP
机械能
kx2
mv2
一、机械能(mechanical energy)
1.概 念:
动能、重力势能和弹性势能的统称
2.表达式:
3.单 位:
焦耳(J)
4.标示性:
标量,具有相对性
E=Ek+EP
思考1:理想斜面实验小球总能回到原来高度说明什么
运动过程中有能保持不变的量
往下跑:动能和重力势能怎么变化?
EP减小、EK增加
往上跑:动能和重力势能怎么变化?
EP增加、EK减小
猜想:运动过程中小球EK和EP在相互转化,
但EK+EP
不变
h1
h2
V1
V2
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
参考平面
思考2:在单摆模型中,每个位置小球的EK+EP是否不变
参考平面
h1
h2
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
结论:在只有重力做功的情况下,EK+EP的和保持不变。
h1
h2
V1
V2
V0
结论:在只有重力做功的情况下,EK+EP的和保持不变
思考3:在各种抛体运动中,小球的EK+EP是否守恒
mg(h1-h2)=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
mgh1-mgh2=
1
2
- mv12
1
2
mv22
EP1+EK1=
EP2+EK2
EK和EP发生互相转化,
二、机械能守恒定律
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
【典例1】若忽略空气阻力的影响,下列运动过程中物体机械能守恒的是( )
A.被掷出后在空中运动的铅球
B.沿粗糙斜面减速下滑的木块
C.随热气球一起匀速上升的吊篮
D.随倾斜传送带加速上行的货物
A
【典例2】荡秋千是一种常见的娱乐休闲活动(如图)。若秋千绳的长度l=2 m,荡到最高点时秋千绳与竖直方向的夹角θ=60°。取重力加速度g=9.8 m/s2,求荡到最低点时秋千的速度大小 (忽略阻力及秋千绳的质量,且人在秋千上的姿势可视为不变)
解:由机械能守恒:EP1+EK1=EP2+EK2
选择最低位置时的水平面为参考平面
mg(l-lcosθ)+
0=
0+
1
2
mv2
得v=
2gl(1-cosθ)
法2: 由机械能守恒EP1-EP2=EK2-EK1
mg(l-lcosθ)=
1
2
mv2-0
得v=
2gl(1-cosθ)
=
法3: 由动能定理WG=EK2-EK1
mg(l-lcosθ)=
1
2
mv2-0
得v=
=
【变式拓展】在现实中,若人在荡秋千时姿势不变,秋千将逐渐停下来,这是有阻力的缘故。因此,人荡秋千时,只有在保持姿势不变且忽略阻力的情况下,其机械能才守恒。为什么有的人可以越荡越高,他是怎么做到的呢?请分析原因。
人荡秋千时越荡越高,是在荡秋千的过程中,人通过做一些合适的动作做功,将人体内的化学能转化为人和秋千的机械能的缘故。
思考:人匀速楼梯,人的机械能是否守恒?
EK和EP发生互相转化,
二、机械能守恒定律
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
注意:
(1)可以受其它力,
但其它力不做功或做功代数和为零。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
(2)因涉及重力势能,所以此定律针对物体
和地球这个系统。
若其它力做了功,
则W非G=ΔE
二、机械能守恒定律
4.应用步骤:
①选对象,受力分析,做功分析。
②定减小的能和增加的能。
③列机守方程求解。
EK和EP发生互相转化,
1.内容:
一个物体在只有重力做功的情形下,物体的
2.表达式:
或
3.成立条件:
只有重力做功。
但总机械能保持不变。
EP1-EP2=
EK2-EK1
EP1+EK1=
EP2+EK2
【典例3】如图所示,两质量相同的小球A、B,分别用长度不同的线悬挂在等高的O1、O2点,A球的悬线比B球的悬线长。把两球的悬线均拉到水平后将小球无初速释放,以悬点为零势能参考面,不计空气阻力。两球经过最低点时,悬线上的拉力分别为FA、FB,所具有的机械能分别为EA和EB。则( )
A.FA=FB、EA=EB
B.FA>FB、EA>EB
C.FA=FB、EA>EB
D.FA>FB、EA=EB
A
思考1:绳拴两物体,在B下落过程中A的E机守恒吗?
结论:A的机械能在增加,ΔE=
WT
思考:由A、B构成的系统机械能守恒吗?
A、B构成的系统机械能守恒。
不计一切阻力
不计一切阻力
思考2:杆连两物体,在转动过程中A球的E机守恒吗?
结论:A的机械能不守恒,ΔE=
W杆
A、B构成的系统机械能守恒。
FN
S
FN
S/
思考:由A、B构成的系统机械能守恒吗?
思考3:直接连接的两物体,在运动过程中E机守恒吗?
结论:单个物体不守恒,但系统机械能守恒
不计一切阻力
不计一切阻力
结论:在只有弹簧弹力做功的情况下,小球的动能和
弹簧的弹性势能每个位置EK+EP的和保持不变。
思考4:小球在和弹簧作用的系统,小球机械能守恒吗?
W弹=
1
2
- mv12
1
2
mv22
W弹=
EP1-EP2
EP1-EP2=
1
2
- mv12
1
2
mv22
EP1-EP2=
EK2-EK1
光滑水平面
原长
F弹
V1
V2
弹簧:
EP1+EK1=
EP2+EK2
思考:小球和弹簧这个系统机械能守恒吗?
结论:小球E不守恒
v0
A
B
A
B
Ff
Ff
l1
l2
Δl
思考5:系统内力中的摩擦力做功对系统的机械能是否影响
A对B做的功WAB=______
B对A做的功WBA=______
Ffl1
-Ffl2
结论:一对内力Ff对系统做负功。导致系统E减小
WAB+WBA=___________
Ffl1-Ffl2
=-FfΔl
VB
VA
-0
1
2
= mBvB2
1
2
- mAv02
1
2
= mAvA2
1
2
= mBvB2
1
2
- mAv02
1
2
+ mAvA2
光滑水平面
FfΔl=
1
2
mAv02
-
1
2
( mBvB2
1
2
+ mAvA2)
=EK初-EK末
三、系统机械能守恒定律
1.内容:
一个系统,若只有系统内力中的弹力做功,
2.表达式:
或
3.成立条件:
只有弹力做功。
注意:
(1)绳、杆、接触弹力对两物体做功抵消,
使E在两物体之间转移,系统E守恒。
每个物体机械能不守恒,但总机械能守恒。
E减=
E增
EP1+EK1=
EP2+EK2
(2)簧弹力对两端物体做功不能抵消,
使E在物体和弹簧间转移。包括弹簧的系统E守恒
(3)Ff对两物体做功不能抵消,
FfΔl==EK初-EK末
【典例4】一轻质理想弹簧一端固定在竖直墙壁上,一端固定在小木块上,如图所示,水平面光滑,用手推动小木块压缩弹簧一段后松手,在小木块反弹过中,下列说法正确的是( )
A.小木块机械能守恒
B.弹簧机械能守恒
C.小木块弹簧构成的系统机械能守恒
D.小木块弹簧构成的系统机械能不守恒
C
原长
F弹
【典例5】如下图所示,小球从高处下落到竖直放置的轻弹簧上,在从释放到将弹簧压缩到最短的整个过程中,下列关于能量的叙述中正确的是( )
A.小球的机械能不守恒,其机械能一直在增加
B.小球的动能先增大后减小,在刚接触弹簧时最大
C.小球和弹簧构成的系统机械能不守恒
D.重力势能、弹性势能和动能之和总保持不变
D
【典例6】如图所示实例中均不考虑空气阻力,系统机械能守恒的是( )
D
【典例7】如图所示,杂技演员在一根弹性绳上表演。位置a、b是弹性绳的两个固定端,ab连线位置是弹性绳的自然状态。演员从某一高度下落,到了ab连线位置之后,与弹性绳一起向下运动,位置c是演员和弹性绳运动的最低点。演员可视为质点,不考虑人的生物能转化,不计弹性绳的质量和空气阻力,则演员从ab连线位置运动到c点的过程中( )
A.演员的机械能保持不变
B.演员的动能不断减小
C.演员的机械能转化为弹性绳的弹性势能
D.演员的重力势能转化为演员的动能
C
【典例8】(多选)A、B两个物体通过一条轻绳跨过定滑轮相连,A的质量大于B的质量,不计各部分的摩擦阻力,如图所示,则释放后下列说法正确的是( )
A. B物体机械能减小
B. A物体机械能增加
C. A、B两物体机械能都不守恒
D. A、B构成的系统机械能守恒
CD
mBg
T
mAg
T
【典例9】(多选)如图所示,在质量分别为m和2m的小球a和b之间,用一根轻质细杆连接,两小球可绕过轻杆中心的水平轴无摩擦转动,现让轻杆处于水平位置,静止释放小球后,重球b向下转动,轻球a向上转动,在转过90°的过程中,以下说法正确的是( )
A.杆对a球不做功
B.杆对a球做负功
C.杆对b球做负功
D.a、b两球总机械能守恒
CD
b
a
0
【典例10】(多选)斜面A置于光滑的水平面上,滑块B置于A上由静止滑下,它们接触面光滑,如图所示,则下列说法正确的是( )
A. A物体机械能守恒
B. B物体机械能守恒
C. A、B两物体机械能都不守恒
D. A、B系统物体机械能守恒
CD
A
A
B
B
FN
G
S
FN
S、
【典例11】一光滑水平面上放着一个静止的木块,其质量为M,一个质量为m的子弹,以初速度v0射入木块,并最终留在木块内一起做匀速运动,则下列说法正确的是( )
A.小木块机械能守恒
B.木板机械能守恒
C.小木块、木板构成的系统机械能守恒
D.小木块、木板构成的系统机械能不守恒
D
v0
v共
S木
S子
摩擦力对子弹做的功W=
f
f
-f
S子
摩擦力对木块做的功W/=
f
S木
两者的功不能抵消
所以系统机械能不守恒
【典例12】一条长为L的均匀链条,放在光滑水平桌面上,链条的一半垂于桌边,如图所示?现由静止开始使链条自由滑落,当它全部脱离桌面时的速度为多大
解:设链条总质量为m
得:
+
-0
