广东省深圳中学2022-2023学年高二下学期期中数学试卷(含解析)
文档属性
| 名称 | 广东省深圳中学2022-2023学年高二下学期期中数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 731.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 07:30:36 | ||
图片预览




文档简介
2022-2023学年广东省深圳中学高二(下)期中数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知函数f(x)=xex,则f′(1)=( )
A.1﹣ B.e C.2e D.e°
2.(5分)对四组数据进行统计,获得以下散点图,则其相关系数值最大的是( )
A.r1 B.r2 C.r3 D.r4
3.(5分)如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则p等于( )
A. B. C. D.
4.(5分)一袋中装有10个球,其中3个黑球、7个白球,从中先后随机各取一球(不放回),则第二次取到的是黑球的概率为( )
A. B. C. D.
5.(5分)已知从某批材料中任取一件时,取得的这件材料的强度X~N(200,182),则取得的这件材料的强度介于182到236之间的概率为( )
附:若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544,P(μ﹣3σ<X<μ+3σ)=0.9974).
A.0.9973 B.0.8665 C.0.8413 D.0.8185
6.(5分)某一离散型随机变量ξ的概率分布如下表,且Eξ=1.5,则a﹣b的值为( )
ξ 0 1 2 3
P 0.1 a b 0.1
A.﹣0.1 B.0 C.0.1 D.0.2
7.(5分)已知函数,则y=f(x)的图象大致为( )
A. B.
C. D.
8.(5分)当0<x<1时,下列不等式正确的是( )
A. B.
C. D.
二、多项选择题(共4小题,每小题均有两个选项符合题意,全对得5分,错选得0分,漏选得2分,共20分).
(多选)9.(5分)关于的展开式,下列结论正确的是( )
A.奇数项的二项式系数和为32
B.所有项的系数和为243
C.只有第3项的二项式系数最大
D.含x项的系数为40
(多选)10.(5分)关于随机事件A,B,C,下列说法正确的是( )
A.若,则A,B独立
B.若P(AB)=P(A)P(B),则
C.若P(A+B)=P(A)+P(B),则P(AB)=P(A)P(B)
D.若事件B和C是两个互斥事件,则P(B∪C|A)=P(B|A)+P(C|A)
(多选)11.(5分)设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
A. x∈R,f(x)≤f(x0)
B.﹣x0是f(﹣x)的极大值点
C.﹣x0是﹣f(x)的极小值点
D.﹣x0是﹣f(﹣x)的极小值点
(多选)12.(5分)已知函数f(x)=ex,g(x)=axm(x>0),其中m≠0,1,则( )
A.存在过点(0,0)与函数f(x)、g(x)图象均相切的直线
B.当,时,不存在与函数f(x)、g(x)图象均相切的直线
C.当,时,存在两条与函数f(x)、g(x)图象均相切的直线
D.最多存在三条与函数f(x)、g(x)图象均相切的直线
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为__________;__________.
14.(5分)甲、乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局比赛都结束,假定甲每局比赛获胜的概率均为,则甲以3:1的比分获胜的概率为__________.
15.(5分)已知随机变量ξ的取值为i(i=0,1,2).若,E(ξ)=1,则D(2ξ﹣3)=__________.
16.(5分)已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0,且x0>0.则a的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,已知长方体ABCD﹣A1B1C1D1,AB=3,AD=2,AA1=2,,.
(1)求异面直线C1E与BF所成角的余弦值;
(2)求平面ADF与平面B1EF所成角的余弦值.
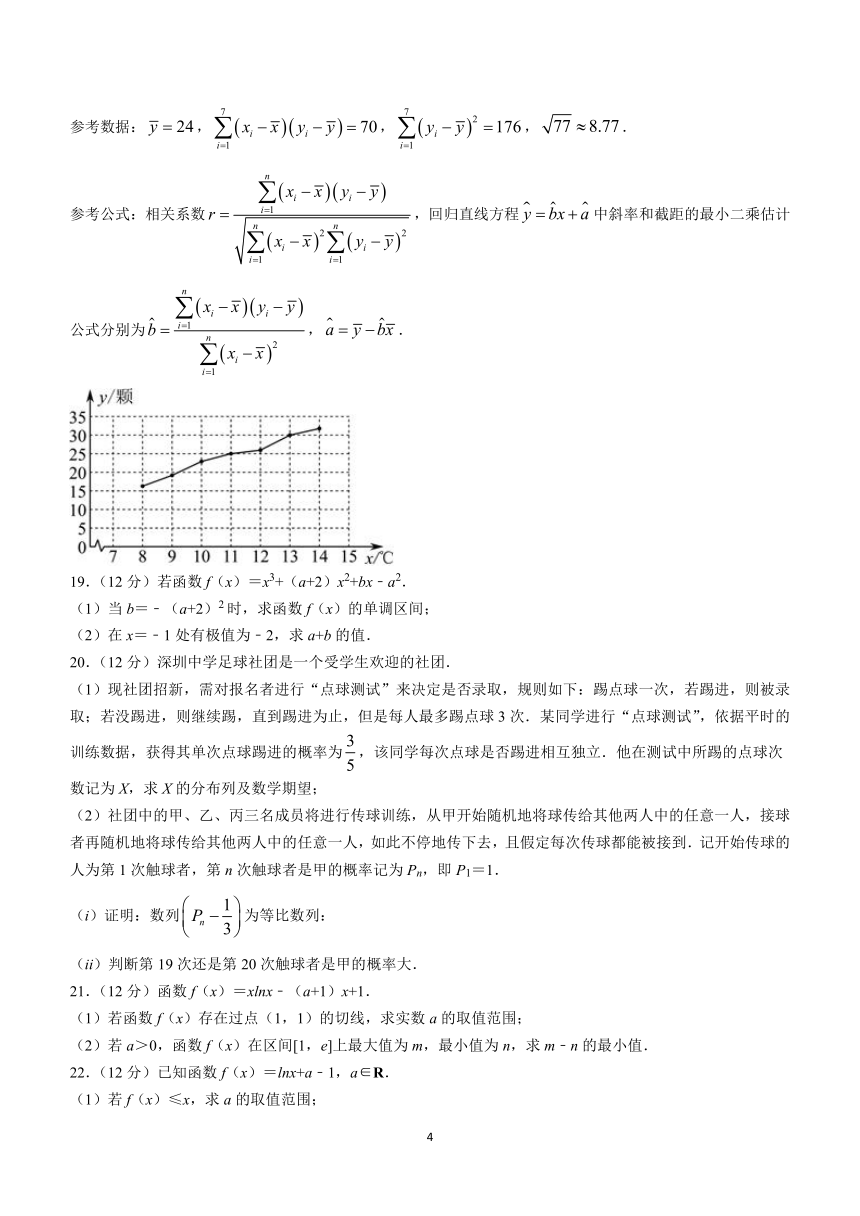
18.(12分)已知某绿豆新品种发芽的适宜温度在6℃~22℃之间,一农学实验室研究人员为研究温度x(℃)与绿豆新品种发芽数y(颗)之间的关系,每组选取了成熟种子50颗,分别在对应的8℃~14℃的温度环境下进行实验,得到如下散点图:
(1)由折线统计图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并预测在19℃的温度下,种子发芽的颗数.
参考数据:,,,.
参考公式:相关系数,回归直线方程中斜率和截距的最小二乘估计公式分别为,.
19.(12分)若函数f(x)=x3+(a+2)x2+bx﹣a2.
(1)当b=﹣(a+2)2时,求函数f(x)的单调区间;
(2)在x=﹣1处有极值为﹣2,求a+b的值.
20.(12分)深圳中学足球社团是一个受学生欢迎的社团.
(1)现社团招新,需对报名者进行“点球测试”来决定是否录取,规则如下:踢点球一次,若踢进,则被录取;若没踢进,则继续踢,直到踢进为止,但是每人最多踢点球3次.某同学进行“点球测试”,依据平时的训练数据,获得其单次点球踢进的概率为,该同学每次点球是否踢进相互独立.他在测试中所踢的点球次数记为X,求X的分布列及数学期望;
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)证明:数列为等比数列:
(ii)判断第19次还是第20次触球者是甲的概率大.
21.(12分)函数f(x)=xlnx﹣(a+1)x+1.
(1)若函数f(x)存在过点(1,1)的切线,求实数a的取值范围;
(2)若a>0,函数f(x)在区间[1,e]上最大值为m,最小值为n,求m﹣n的最小值.
22.(12分)已知函数f(x)=lnx+a﹣1,a∈R.
(1)若f(x)≤x,求a的取值范围;
(2)当a∈(0,1]时,证明:.
2022-2023学年广东省深圳中学高二(下)期中数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【分析】利用导数的运算性质求出函数的导数,然后令x=1即可求解.
【解答】解:由已知可得f′(x)=ex+xex,
则f′(1)=e+e=2e.
故选:C.
【点评】本题考查了导数的运算性质,属于基础题.
2.【分析】根据相关系数的定义|r|的值越接近于1关联性越强,结合图象即可求解.
【解答】解:根据相关系数的定义知,|r|越接近于1关联性越强,
结合图象知,第一、三两幅图为正相关,且第一幅图的相关性较强,所以0<r3<r1,
又因为第二、四幅图变量之间为负相关,且第二幅图的相关性较强,所以r2<r4<0,
故选:A.
【点评】本题考查了相关系数的定义与应用问题,是基础题.
3.【分析】因为ξ服从二项分布,由二项分布的期望和方差公式Eξ=np,Dξ=np(1﹣p)解出p即可.
【解答】解:如果随机变量ξ~B(n,p),则Eξ=np,Dξ=np(1﹣p)又Eξ=7,Dξ=6,
∴np=7,np(1﹣p)=6,.
故选:A.
【点评】本题考查二项分布的期望和方差公式,属基本题型基本方法的考查.
4.【分析】根据已知条件,结合古典概型的概率公式,即可求解.
【解答】解:由题意可得,第二次取到的是黑球的概率为.
故选:C.
【点评】本题主要考查古典概型的概率公式,属于基础题.
5.【分析】本题根据正态分布对称性的性质,即可求出答案.
【解答】解:因为取得的这件材料的强度X~N(200,182),
所以μ=200,σ=18,
则P(182<X<218)=0.6826,P(164<X<236)=0.9544,
,
所以P(182<X<236)=0.9544﹣0.1359=0.8185.
故选:D.
【点评】本题考查正态分布曲线的性质,属于基础题.
6.【分析】根据题意,由分布列的性质可得a+b=0.8,又由期望的计算公式可得a+2b=0.8,联立两个式子可得a、b的值,进而计算可得答案.
【解答】解:根据题意,分布列可得:0.1+a+b+0.1=1,则有a+b=0.8①,
又由Eξ=1.5,即0×0.1+a+2b+0.3=1.5,则有a+2b=0.8②,
联立①②可得:a=b=0.4,则a﹣b=0.
故选:B.
【点评】本题考查随机变量的分布列,涉及随机变量的期望,属于基础题.
7.【分析】考虑函数f(x)的分母的函数值恒小于零,即可排除A,C,由f(x)的定义域能排除D,这一性质可利用导数加以证明
【解答】解:设
则
∴g(x)在(﹣1,0)上为增函数,在(0,+∞)上为减函数
∴g(x)<g(0)=0
得:x>0或﹣1<x<0均有f(x)>0排除A,C,
又中,,能排除D.
故选:B.
【点评】本题主要考查了函数解析式与函数图象间的关系,利用导数研究函数性质的应用,排除法解图象选择题,属基础题
8.【分析】利用导数法分析在区间(0,1)上的单调性,并分析函数的值域,进而可得答案.
【解答】解:令,
则,
当x∈(0,1)时,,x﹣tanx<0,
故f′(x)<0,
故在区间(0,1)上单调递减,
由0<x2<x<1,
,
又,
故,
综上:,
故选:C.
【点评】本题考查的知识点是利用导数研究函数的单调性,其中分析出在区间(0,1)上的单调性,是解答的关键.
二、多项选择题(共4小题,每小题均有两个选项符合题意,全对得5分,错选得0分,漏选得2分,共20分).
9.【分析】由二项展开式的二项式系数的性质判断AC;取x=1求得所有项的系数和判断B;写出展开式的通项,由x的指数为1求得r值,可得含x项的系数判断D.
【解答】解:的展开式的所有二项式系数和为25=32,奇数项的二项式系数和为16,故A错误;
取x=1,可得所有项的系数和为35=243,故B正确;
的展开式有6项,第3项与第4项的二项式系数相等且最大,故C错误;
展开式的通项为,
由5﹣2r=1,得r=2,
∴含x项的系数为,故D正确.
故选:BD.
【点评】本题考查二项式系数的性质,关键是熟记二项展开式的通项,是基础题.
10.【分析】由条件概率公式及独立事件的定义判断A,由独立事件的定义判断B,举实例判断C,由互斥事件的概率加法公式判断D.
【解答】解:A,若,
则P(B)=P(A)P(B|A)+P()P(B|),
∴P(AB)=P(A)P(B),∴A,B独立∴正确,
B,若P(AB)=P(A)P(B),则A,B独立,,独立,
,∴正确,
C,投掷一枚质地均匀的骰子,设出现偶数点为事件A,出现奇数点为事件B,事件A和B是两个对立事件,
则P(A)+P(B)=1,,P(AB)=0,
∴P(AB)≠P(A)P(B),∴错误,
D,若事件B和C是两个互斥事件,由互斥事件的概率加法公式,
则P(B∪C|A)=P(B|A)+P(C|A),∴正确.
故选:ABD.
【点评】本题考查条件概率,相互独立事件,互斥事件的概率公式,属于中档题.
11.【分析】根据函数的单调性和对称性分别判断即可.
【解答】解:对于A,x0(x0≠0)是f(x)的极大值点,不一定是最大值点,
故不能满足在整个定义域上的值最大,故A错误,
对于B,f(﹣x)是把f(x)的图像转化为关于y轴对称,
故﹣x0是f(﹣x)的极大值点,故B正确,
对于C,﹣f(x)是把f(x)的图像转化为关于x轴对称,
故﹣x0是﹣f(x)的极大值点,故C错误,
对于D,﹣f(﹣x)是把f(x)的图像转化为分别关于x轴,y轴作对称,
故﹣x0是﹣f(﹣x)的极小值点,故D正确,
故选:BD.
【点评】本题考查了利用导数研究函数的单调性极值与最值、考查对称性问题以及推理能力与计算能力,属于中档题.
12.【分析】由题意,对选项A,因为函数g(x)的图象恒过定点(0,0),得到g(x)的切线方程,进而可判断;对于选项B,将m=2,代入两函数解析式中,假设存在公切线与f(x)切点P1(x1,y1),P2(x2,y2),得到两函数关于切点的切线方程,列出不等式再求解,设立新函数,对新函数进行求导,利用导数得到该函数的单调性和最值,进而即可求解,同理可得选项C和选项D.
【解答】解:已知f(x)=ex,g(x)=axm(m≠0,1),函数定义域为(0,+∞),
可得f′(x)=ex,g′(x)=amxm﹣1,
对于选项A,易知函数g(x)的图象恒过定点(0,0),
所以切线斜率k=0,
切线方程为y=0,
显然y=0不是函数f(x)的切线,故选项A错误;
对于选项B,当m=2,时,
,
g′(x)=ex,
假设存在公切线与f(x)切点P1(x1,y1),P2(x2,y2),
所以函数f(x)在点P1处的切线方程为,
即,
函数g(x)在点P2处的切线方程为y﹣y2=ex2(x﹣x2),
即,
其满足,
所以,
此时,
整理得,
即,①
不妨设h(x)=ex﹣1﹣2x+2,函数定义域为R,
可得h′(x)=ex﹣1﹣2,
当x<1+ln2时,h′(x)<0,h(x)单调递减;
当x>1+ln2时,h′(x)>0,h(x)单调递增,
所以h(x)在x=1+ln2上取得极小值也是最小值,
所以h(x)≥h(1+ln2)=2﹣2ln2>0,
其不满足①式,故P1不存在,
所以不存在与函数f(x)、g(x)图象均相切的直线,
故选项B正确;
对于选项C,当,时,
,
可得,
假设存在公切线与f(x)切点P3(x3,y3),P4(x4,y4),
所以函数f(x)在点P3处的切线方程为,
即y=x﹣(x3﹣1),
函数g(x)在点P4处的切线方程为,
即,
其满足,
所以,
即,②
不妨设,函数定义域为R,
可得k′(x)=﹣e2x+2(1﹣x)e2x=e2x(1﹣2x),
当时,k′(x)>0,k(x)单调递增;
当时,k′(x)<0,k(x)单调递减,
所以k(x)在上取得极大值也是最大值,
所以,
此时方程②有两解,
所以至多存在一条公切线,故选项C正确;
对于选项D,当,时,
函数f(x)、g(x)至多存在两条公切线,
故选项D错误.
故选:BC.
【点评】本题考查切线方程和利用导数研究函数的单调性,考查方程思想、推理能力和运算能力.
三、填空题:本题共4小题,每小题5分,共20分。
13.【分析】根据已知条件,结合列联表之间的数据关系,即可求解.
【解答】解:由表中数据可,a=73﹣21=52,
b=a+8=52+8=60.
故答案为:52;60.
【点评】本题主要考查列联表的应用,属于基础题.
14.【分析】以甲3胜1负而结束比赛,甲只能在1、2、3局中负1局,第4局胜,即可得出结论.
【解答】解:甲以3:1的比分获胜,甲只能在1、2、3局中负1局,第4局胜,
因此所求概率为:.
故答案为:.
【点评】本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,属于基础题.
15.【分析】根据已知条件,结合离散型随机变量分布列的性质,以及期望公式,求出,再结合方差公式,即可求解.
【解答】解:随机变量ξ的取值为i(i=0,1,2),P(ξ=0)=,E(ξ)=1,
则,解得,
所以,
故D(2ξ﹣3)=22D(ξ)=.
故答案为:.
【点评】本题主要考查离散型随机变量期望与方差的求解,考查转化能力,属于中档题.
16.【分析】分类讨论:当a≥0时,容易判断出不符合题意;当a<0时,求出函数的导数,利用导数和极值之间的关系转化为求极小值f()>0,解出即可.
【解答】解:当a=0时,f(x)=﹣3x2+1=0,解得,函数f(x)有两个零点,不符合题意,应舍去;
当a>0时,令f′(x)=3ax2﹣6x=3ax(x﹣)=0,解得x=0或x=>0,列表如下:
x (﹣∞,0) 0 (0,) (,+∞)
f′(x) + 0 ﹣ 0 +
f(x) 单调递增 极大值 单调递减 极小值 单调递增
∵x→﹣∞,f(x)→﹣∞,而f(0)=1>0,∴存在x<0,使得f(x)=0,
不符合条件:f(x)存在唯一的零点x0,且x0>0,应舍去.
当a<0时,f′(x)=3ax2﹣6x=3ax(x﹣)=0,解得x=0或x=<0,列表如下:
x (﹣∞,) (,0) 0 (0,+∞)
f′(x) ﹣ 0 + 0 ﹣
f(x) 单调递减 极小值 单调递增 极大值 单调递减
而f(0)=1>0,x→+∞时,f(x)→﹣∞,∴存在x0>0,使得f(x0)=0,
∵f(x)存在唯一的零点x0,且x0>0,∴极小值f()=a()3﹣3()2+1>0,
化为a2>4,
∵a<0,∴a<﹣2.
综上可知:a的取值范围是(﹣∞,﹣2).
故答案为:(﹣∞,﹣2).
【点评】本题考查了利用导数研究函数的单调性极值与最值、分类讨论的思想方法,考查了推理能力和计算能力,属于难题.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.【分析】(1)建立空间直角坐标系,求得,,利用异面直线所成角公式即可求解;
(2)分别求得平面ADF的法向量为,平面B1EF的法向量为,代入二面角公式即可求解.
【解答】解:(1)建立如图空间直角坐标系,
∵AB=3,AD=2,AA1=2,,,
∴C1(0,3,2),E(2,1,0),B(2,3,0),F(0,3,1),A(2,0,0),B1(2,3,2),D(0,0,0),
,,
则异面直线C1E与BF所成角的余弦值为;
(2)由(1)知,,
设平面ADF的法向量为,
则,
令y=1,则z=﹣3,
∴平面ADF的法向量为,
,,
设平面B1EF的法向量为,
则,令b=1,则c=﹣1,,
∴平面B1EF的法向量为,
平面ADF与平面B1EF所成角的余弦值为.
【点评】本题考查了异面直线所成角和二面角的计算,属于中档题.
18.【分析】(1)直接套公式求出系数r,即可判断;(2)套公式求出回归方程,把x=19代入,即可求解.
【解答】解:(1)由题意可知:,
则,
又,
所以相关系数.
所以y与x的线性相关性较高,可以利用线性回归模型拟合y与x的关系.
(2)由(1)知,,,.
所以,
所以.
所以y与x的回归直线为y=2.5x﹣3.5.
当x=19时,y=2.5×19﹣3.5=44.即在19℃的温度下,种子发芽的颗数为44.
【点评】本题主要考查了相关系数的求解及应用,还考查了线性回归方程的应用,属于中档题.
19.【分析】(1)求导数并求出导数的零点、﹣(a+2),讨论(a+2)的符号,解出导数大于零、小于零或等于零的解,得到原函数的单调区间;
(2)求出导数,然后根据极值点处的导数为0,导数值为﹣2,列出a,b的方程组,最后利用导函数为零所得方程的判别式验证即可.
【解答】解:由题知定义域为R,f′(x)=3x2+2(a+2)x+b,
(1)令f′(x)=3x2+2(a+2)x﹣(a+2)2=0得或﹣(a+2),
①当a+2>0,即a>﹣2时,f′(x)>0 x<﹣(a+2)或x>,f′(x)<0 ﹣(a+2)<x<,
所以f(x)的单调递增区间为(﹣∞,﹣(a+2)),(,+∞);单调递减区间为(﹣(a+2),);
同理得:
②当a+2<0,即a<﹣2时,f(x)的单调递增区间为(﹣(a+2),+∞),(﹣∞,);单调递减区间为(,﹣(a+2));
③当a+2=0,即a=﹣2时,f′(x)≥0恒成立,f(x)是增函数.
(2)由题意得,解得或,
令f′(x)=3x2+2(a+2)x+b=0,
当时,Δ=4(a+2)2﹣12b=36>0,符合题意;
当时,Δ=0,此时f′(x)≥0恒成立,不符合题意,
故a+b=﹣5即为所求.
【点评】本题考查利用导数研究函数单调区间的方法,极值点处性质的应用,属于中档题.
20.【分析】(1)由题意,X可能取1,2,3,计算出各自对应的概率即可求解;
(2)(i)第n次触球者是甲的概率记为Pn,则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,则,化简整理即可得证;
(ii)由(i)知,代入整理即可求解.
【解答】解:(1)由题意,X可能取1,2,3,
则P(X=1)=0.6,P(X=2)=0.4×0.6=0.24,
P(X=3)=0.4×0.4=0.16,
X的分布列为:
X 1 2 3
P 0.6 0.24 0.16
即E(X)=1×0.6+2×0.24+3×0.16=1.56;
(2)证明:(i)第n次触球者是甲的概率记为Pn,则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,
则,
从而,又,
是以为首项,公比为的等比数列;
(ii),,
,
P19>P20,故第19次触球者是甲的概率大.
【点评】本题考查了离散型随机变量的分布列与期望,属于中档题.
21.【分析】(1)设切线切于点P(t,tlnt﹣(a+1)t+1),从而得切线方程为y﹣tlnt+(a+1)t﹣1=(lnt﹣a)(x﹣t),再将(1,1)代入切线方程,最后再根据题意可得关于t的方程有解,从而可得a的范围;
(2)分类讨论a,求出m,n,得到m﹣n,再构造函数求出最小值即可得解.
【解答】解:(1)f(x)的定义域为(0,+∞),f′(x)=lnx+1﹣(a+1)=lnx﹣a,
设切线切于点P(t,tlnt﹣(a+1)t+1),
则切点P处的切线方程为y﹣tlnt+(a+1)t﹣1=(lnt﹣a)(x﹣t),又该切线过(1,1),
∴1﹣tlnt+(a+1)t﹣1=(lnt﹣a)(1﹣t)在t>0上有解,
即a=lnt﹣t在t>0上有解,
设g(x)=lnx﹣x,x>0,,x>0,
∴当x∈(0,1)时,g′(x)>0,g(x)单调递增;
当x∈(1,+∞)时,g′(x)<0,g(x)单调递减,
∴g(x)≤g(1)=﹣1,
∴a=lnt﹣t在t>0上有解,
则a≤﹣1,∴实数a的取值范围为(﹣∞,﹣1];
(2)f′(x)=lnx﹣a,x∈[1,e],lnx∈[0,1],
①当a≥1时,f′(x)≤0恒成立,函数f(x)在区间[1,e]上为减函数,
所以m=f(1)=﹣a,n=f(e)=1﹣ae,所以m﹣n=(e﹣1)a﹣1,
令h(a)=(e﹣1)a﹣1,则函数h(a)在区间[1,+∞)上单调递增,
所以h(a)的最小值为h(1)=e﹣2,即m﹣n的最小值为e﹣2.
②当0<a<1时,由f′(x)>0,得ea<x≤e,由f′(x)<0,得1≤x<ea,
所以f(x)在区间[1,ea)上单调递减,在(ea,e]上单调递增,
所以n=f(ea)=1﹣ea,
当≤a<1时,f(1)﹣f(e)=(e﹣1)a﹣1≥0,此时m=f(1)=﹣a,
所以m﹣n=f(1)﹣f(ea)=ea﹣a﹣1,
令φ(a)=ea﹣a﹣1,φ′(a)=ea﹣1>0,
所以φ(a)在区间[,1)上单调递增,
所以函数φ(a)的最小值为;
当0<a<时,f(1)﹣f(e)=(e﹣1)a﹣1<0,所以m=f(e)=1﹣ae,
所以m﹣n=f(e)﹣f(ea)=ea﹣ae,
令q(a)=ea﹣ae,则q′(a)=ea﹣e<0,
所以函数q(a)在区间(0,)上单调递减,
所以,
综上所述,m﹣n的最小值为.
【点评】本题主要考查方程有解问题,利用导数研究函数的单调性与最值,分类讨论思想,属难题.
22.【分析】(1)构造g(x)=f(x)﹣x=lnx﹣x+a﹣1,利用导数的性质判断g(x)的单调性进行求解即可;
(2)构造,利用导数的性质判断h(x)的单调性,结合函数零点存在原理进行求解即可.
【解答】解:(1)记g(x)=f(x)﹣x=lnx﹣x+a﹣1.
则g(x)≤0恒成立,即g(x)max≤0,
,当x∈(0,1),g'(x)>0;当x∈(1,+∞),g'(x)<0;
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)max=g(1)≤0,解得a≤2.∴实数a的取值范围是(﹣∞,2].
(2)证明:记,
,∵在(0,+∞)上单调递增.
令,,
则,所以φ(x)即h'(x)在(0,+∞)上单调递增.
由a∈(0,1],知,,,,即,
∴当x∈(0,x0),h'(x)<0,h(x)单调递减;当x∈(x0,+∞),h'(x)>0,h(x)单调递增,
,
由(*)式,可得,,
代入(**)式,得,
由(1)知,当a=2时有lnx≤x﹣1,
故﹣lnx0≥1﹣x0.,
由,∴h(x0)≥0,
故h(x)≥0,即,原不等式得证.
【点评】本题主要考查利用导数研究函数的单调性与最值,考查不等式的证明,考查运算求解能力与逻辑推理能力,属于难题.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知函数f(x)=xex,则f′(1)=( )
A.1﹣ B.e C.2e D.e°
2.(5分)对四组数据进行统计,获得以下散点图,则其相关系数值最大的是( )
A.r1 B.r2 C.r3 D.r4
3.(5分)如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则p等于( )
A. B. C. D.
4.(5分)一袋中装有10个球,其中3个黑球、7个白球,从中先后随机各取一球(不放回),则第二次取到的是黑球的概率为( )
A. B. C. D.
5.(5分)已知从某批材料中任取一件时,取得的这件材料的强度X~N(200,182),则取得的这件材料的强度介于182到236之间的概率为( )
附:若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544,P(μ﹣3σ<X<μ+3σ)=0.9974).
A.0.9973 B.0.8665 C.0.8413 D.0.8185
6.(5分)某一离散型随机变量ξ的概率分布如下表,且Eξ=1.5,则a﹣b的值为( )
ξ 0 1 2 3
P 0.1 a b 0.1
A.﹣0.1 B.0 C.0.1 D.0.2
7.(5分)已知函数,则y=f(x)的图象大致为( )
A. B.
C. D.
8.(5分)当0<x<1时,下列不等式正确的是( )
A. B.
C. D.
二、多项选择题(共4小题,每小题均有两个选项符合题意,全对得5分,错选得0分,漏选得2分,共20分).
(多选)9.(5分)关于的展开式,下列结论正确的是( )
A.奇数项的二项式系数和为32
B.所有项的系数和为243
C.只有第3项的二项式系数最大
D.含x项的系数为40
(多选)10.(5分)关于随机事件A,B,C,下列说法正确的是( )
A.若,则A,B独立
B.若P(AB)=P(A)P(B),则
C.若P(A+B)=P(A)+P(B),则P(AB)=P(A)P(B)
D.若事件B和C是两个互斥事件,则P(B∪C|A)=P(B|A)+P(C|A)
(多选)11.(5分)设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
A. x∈R,f(x)≤f(x0)
B.﹣x0是f(﹣x)的极大值点
C.﹣x0是﹣f(x)的极小值点
D.﹣x0是﹣f(﹣x)的极小值点
(多选)12.(5分)已知函数f(x)=ex,g(x)=axm(x>0),其中m≠0,1,则( )
A.存在过点(0,0)与函数f(x)、g(x)图象均相切的直线
B.当,时,不存在与函数f(x)、g(x)图象均相切的直线
C.当,时,存在两条与函数f(x)、g(x)图象均相切的直线
D.最多存在三条与函数f(x)、g(x)图象均相切的直线
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为__________;__________.
14.(5分)甲、乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局比赛都结束,假定甲每局比赛获胜的概率均为,则甲以3:1的比分获胜的概率为__________.
15.(5分)已知随机变量ξ的取值为i(i=0,1,2).若,E(ξ)=1,则D(2ξ﹣3)=__________.
16.(5分)已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0,且x0>0.则a的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,已知长方体ABCD﹣A1B1C1D1,AB=3,AD=2,AA1=2,,.
(1)求异面直线C1E与BF所成角的余弦值;
(2)求平面ADF与平面B1EF所成角的余弦值.
18.(12分)已知某绿豆新品种发芽的适宜温度在6℃~22℃之间,一农学实验室研究人员为研究温度x(℃)与绿豆新品种发芽数y(颗)之间的关系,每组选取了成熟种子50颗,分别在对应的8℃~14℃的温度环境下进行实验,得到如下散点图:
(1)由折线统计图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并预测在19℃的温度下,种子发芽的颗数.
参考数据:,,,.
参考公式:相关系数,回归直线方程中斜率和截距的最小二乘估计公式分别为,.
19.(12分)若函数f(x)=x3+(a+2)x2+bx﹣a2.
(1)当b=﹣(a+2)2时,求函数f(x)的单调区间;
(2)在x=﹣1处有极值为﹣2,求a+b的值.
20.(12分)深圳中学足球社团是一个受学生欢迎的社团.
(1)现社团招新,需对报名者进行“点球测试”来决定是否录取,规则如下:踢点球一次,若踢进,则被录取;若没踢进,则继续踢,直到踢进为止,但是每人最多踢点球3次.某同学进行“点球测试”,依据平时的训练数据,获得其单次点球踢进的概率为,该同学每次点球是否踢进相互独立.他在测试中所踢的点球次数记为X,求X的分布列及数学期望;
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)证明:数列为等比数列:
(ii)判断第19次还是第20次触球者是甲的概率大.
21.(12分)函数f(x)=xlnx﹣(a+1)x+1.
(1)若函数f(x)存在过点(1,1)的切线,求实数a的取值范围;
(2)若a>0,函数f(x)在区间[1,e]上最大值为m,最小值为n,求m﹣n的最小值.
22.(12分)已知函数f(x)=lnx+a﹣1,a∈R.
(1)若f(x)≤x,求a的取值范围;
(2)当a∈(0,1]时,证明:.
2022-2023学年广东省深圳中学高二(下)期中数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【分析】利用导数的运算性质求出函数的导数,然后令x=1即可求解.
【解答】解:由已知可得f′(x)=ex+xex,
则f′(1)=e+e=2e.
故选:C.
【点评】本题考查了导数的运算性质,属于基础题.
2.【分析】根据相关系数的定义|r|的值越接近于1关联性越强,结合图象即可求解.
【解答】解:根据相关系数的定义知,|r|越接近于1关联性越强,
结合图象知,第一、三两幅图为正相关,且第一幅图的相关性较强,所以0<r3<r1,
又因为第二、四幅图变量之间为负相关,且第二幅图的相关性较强,所以r2<r4<0,
故选:A.
【点评】本题考查了相关系数的定义与应用问题,是基础题.
3.【分析】因为ξ服从二项分布,由二项分布的期望和方差公式Eξ=np,Dξ=np(1﹣p)解出p即可.
【解答】解:如果随机变量ξ~B(n,p),则Eξ=np,Dξ=np(1﹣p)又Eξ=7,Dξ=6,
∴np=7,np(1﹣p)=6,.
故选:A.
【点评】本题考查二项分布的期望和方差公式,属基本题型基本方法的考查.
4.【分析】根据已知条件,结合古典概型的概率公式,即可求解.
【解答】解:由题意可得,第二次取到的是黑球的概率为.
故选:C.
【点评】本题主要考查古典概型的概率公式,属于基础题.
5.【分析】本题根据正态分布对称性的性质,即可求出答案.
【解答】解:因为取得的这件材料的强度X~N(200,182),
所以μ=200,σ=18,
则P(182<X<218)=0.6826,P(164<X<236)=0.9544,
,
所以P(182<X<236)=0.9544﹣0.1359=0.8185.
故选:D.
【点评】本题考查正态分布曲线的性质,属于基础题.
6.【分析】根据题意,由分布列的性质可得a+b=0.8,又由期望的计算公式可得a+2b=0.8,联立两个式子可得a、b的值,进而计算可得答案.
【解答】解:根据题意,分布列可得:0.1+a+b+0.1=1,则有a+b=0.8①,
又由Eξ=1.5,即0×0.1+a+2b+0.3=1.5,则有a+2b=0.8②,
联立①②可得:a=b=0.4,则a﹣b=0.
故选:B.
【点评】本题考查随机变量的分布列,涉及随机变量的期望,属于基础题.
7.【分析】考虑函数f(x)的分母的函数值恒小于零,即可排除A,C,由f(x)的定义域能排除D,这一性质可利用导数加以证明
【解答】解:设
则
∴g(x)在(﹣1,0)上为增函数,在(0,+∞)上为减函数
∴g(x)<g(0)=0
得:x>0或﹣1<x<0均有f(x)>0排除A,C,
又中,,能排除D.
故选:B.
【点评】本题主要考查了函数解析式与函数图象间的关系,利用导数研究函数性质的应用,排除法解图象选择题,属基础题
8.【分析】利用导数法分析在区间(0,1)上的单调性,并分析函数的值域,进而可得答案.
【解答】解:令,
则,
当x∈(0,1)时,,x﹣tanx<0,
故f′(x)<0,
故在区间(0,1)上单调递减,
由0<x2<x<1,
,
又,
故,
综上:,
故选:C.
【点评】本题考查的知识点是利用导数研究函数的单调性,其中分析出在区间(0,1)上的单调性,是解答的关键.
二、多项选择题(共4小题,每小题均有两个选项符合题意,全对得5分,错选得0分,漏选得2分,共20分).
9.【分析】由二项展开式的二项式系数的性质判断AC;取x=1求得所有项的系数和判断B;写出展开式的通项,由x的指数为1求得r值,可得含x项的系数判断D.
【解答】解:的展开式的所有二项式系数和为25=32,奇数项的二项式系数和为16,故A错误;
取x=1,可得所有项的系数和为35=243,故B正确;
的展开式有6项,第3项与第4项的二项式系数相等且最大,故C错误;
展开式的通项为,
由5﹣2r=1,得r=2,
∴含x项的系数为,故D正确.
故选:BD.
【点评】本题考查二项式系数的性质,关键是熟记二项展开式的通项,是基础题.
10.【分析】由条件概率公式及独立事件的定义判断A,由独立事件的定义判断B,举实例判断C,由互斥事件的概率加法公式判断D.
【解答】解:A,若,
则P(B)=P(A)P(B|A)+P()P(B|),
∴P(AB)=P(A)P(B),∴A,B独立∴正确,
B,若P(AB)=P(A)P(B),则A,B独立,,独立,
,∴正确,
C,投掷一枚质地均匀的骰子,设出现偶数点为事件A,出现奇数点为事件B,事件A和B是两个对立事件,
则P(A)+P(B)=1,,P(AB)=0,
∴P(AB)≠P(A)P(B),∴错误,
D,若事件B和C是两个互斥事件,由互斥事件的概率加法公式,
则P(B∪C|A)=P(B|A)+P(C|A),∴正确.
故选:ABD.
【点评】本题考查条件概率,相互独立事件,互斥事件的概率公式,属于中档题.
11.【分析】根据函数的单调性和对称性分别判断即可.
【解答】解:对于A,x0(x0≠0)是f(x)的极大值点,不一定是最大值点,
故不能满足在整个定义域上的值最大,故A错误,
对于B,f(﹣x)是把f(x)的图像转化为关于y轴对称,
故﹣x0是f(﹣x)的极大值点,故B正确,
对于C,﹣f(x)是把f(x)的图像转化为关于x轴对称,
故﹣x0是﹣f(x)的极大值点,故C错误,
对于D,﹣f(﹣x)是把f(x)的图像转化为分别关于x轴,y轴作对称,
故﹣x0是﹣f(﹣x)的极小值点,故D正确,
故选:BD.
【点评】本题考查了利用导数研究函数的单调性极值与最值、考查对称性问题以及推理能力与计算能力,属于中档题.
12.【分析】由题意,对选项A,因为函数g(x)的图象恒过定点(0,0),得到g(x)的切线方程,进而可判断;对于选项B,将m=2,代入两函数解析式中,假设存在公切线与f(x)切点P1(x1,y1),P2(x2,y2),得到两函数关于切点的切线方程,列出不等式再求解,设立新函数,对新函数进行求导,利用导数得到该函数的单调性和最值,进而即可求解,同理可得选项C和选项D.
【解答】解:已知f(x)=ex,g(x)=axm(m≠0,1),函数定义域为(0,+∞),
可得f′(x)=ex,g′(x)=amxm﹣1,
对于选项A,易知函数g(x)的图象恒过定点(0,0),
所以切线斜率k=0,
切线方程为y=0,
显然y=0不是函数f(x)的切线,故选项A错误;
对于选项B,当m=2,时,
,
g′(x)=ex,
假设存在公切线与f(x)切点P1(x1,y1),P2(x2,y2),
所以函数f(x)在点P1处的切线方程为,
即,
函数g(x)在点P2处的切线方程为y﹣y2=ex2(x﹣x2),
即,
其满足,
所以,
此时,
整理得,
即,①
不妨设h(x)=ex﹣1﹣2x+2,函数定义域为R,
可得h′(x)=ex﹣1﹣2,
当x<1+ln2时,h′(x)<0,h(x)单调递减;
当x>1+ln2时,h′(x)>0,h(x)单调递增,
所以h(x)在x=1+ln2上取得极小值也是最小值,
所以h(x)≥h(1+ln2)=2﹣2ln2>0,
其不满足①式,故P1不存在,
所以不存在与函数f(x)、g(x)图象均相切的直线,
故选项B正确;
对于选项C,当,时,
,
可得,
假设存在公切线与f(x)切点P3(x3,y3),P4(x4,y4),
所以函数f(x)在点P3处的切线方程为,
即y=x﹣(x3﹣1),
函数g(x)在点P4处的切线方程为,
即,
其满足,
所以,
即,②
不妨设,函数定义域为R,
可得k′(x)=﹣e2x+2(1﹣x)e2x=e2x(1﹣2x),
当时,k′(x)>0,k(x)单调递增;
当时,k′(x)<0,k(x)单调递减,
所以k(x)在上取得极大值也是最大值,
所以,
此时方程②有两解,
所以至多存在一条公切线,故选项C正确;
对于选项D,当,时,
函数f(x)、g(x)至多存在两条公切线,
故选项D错误.
故选:BC.
【点评】本题考查切线方程和利用导数研究函数的单调性,考查方程思想、推理能力和运算能力.
三、填空题:本题共4小题,每小题5分,共20分。
13.【分析】根据已知条件,结合列联表之间的数据关系,即可求解.
【解答】解:由表中数据可,a=73﹣21=52,
b=a+8=52+8=60.
故答案为:52;60.
【点评】本题主要考查列联表的应用,属于基础题.
14.【分析】以甲3胜1负而结束比赛,甲只能在1、2、3局中负1局,第4局胜,即可得出结论.
【解答】解:甲以3:1的比分获胜,甲只能在1、2、3局中负1局,第4局胜,
因此所求概率为:.
故答案为:.
【点评】本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,属于基础题.
15.【分析】根据已知条件,结合离散型随机变量分布列的性质,以及期望公式,求出,再结合方差公式,即可求解.
【解答】解:随机变量ξ的取值为i(i=0,1,2),P(ξ=0)=,E(ξ)=1,
则,解得,
所以,
故D(2ξ﹣3)=22D(ξ)=.
故答案为:.
【点评】本题主要考查离散型随机变量期望与方差的求解,考查转化能力,属于中档题.
16.【分析】分类讨论:当a≥0时,容易判断出不符合题意;当a<0时,求出函数的导数,利用导数和极值之间的关系转化为求极小值f()>0,解出即可.
【解答】解:当a=0时,f(x)=﹣3x2+1=0,解得,函数f(x)有两个零点,不符合题意,应舍去;
当a>0时,令f′(x)=3ax2﹣6x=3ax(x﹣)=0,解得x=0或x=>0,列表如下:
x (﹣∞,0) 0 (0,) (,+∞)
f′(x) + 0 ﹣ 0 +
f(x) 单调递增 极大值 单调递减 极小值 单调递增
∵x→﹣∞,f(x)→﹣∞,而f(0)=1>0,∴存在x<0,使得f(x)=0,
不符合条件:f(x)存在唯一的零点x0,且x0>0,应舍去.
当a<0时,f′(x)=3ax2﹣6x=3ax(x﹣)=0,解得x=0或x=<0,列表如下:
x (﹣∞,) (,0) 0 (0,+∞)
f′(x) ﹣ 0 + 0 ﹣
f(x) 单调递减 极小值 单调递增 极大值 单调递减
而f(0)=1>0,x→+∞时,f(x)→﹣∞,∴存在x0>0,使得f(x0)=0,
∵f(x)存在唯一的零点x0,且x0>0,∴极小值f()=a()3﹣3()2+1>0,
化为a2>4,
∵a<0,∴a<﹣2.
综上可知:a的取值范围是(﹣∞,﹣2).
故答案为:(﹣∞,﹣2).
【点评】本题考查了利用导数研究函数的单调性极值与最值、分类讨论的思想方法,考查了推理能力和计算能力,属于难题.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.【分析】(1)建立空间直角坐标系,求得,,利用异面直线所成角公式即可求解;
(2)分别求得平面ADF的法向量为,平面B1EF的法向量为,代入二面角公式即可求解.
【解答】解:(1)建立如图空间直角坐标系,
∵AB=3,AD=2,AA1=2,,,
∴C1(0,3,2),E(2,1,0),B(2,3,0),F(0,3,1),A(2,0,0),B1(2,3,2),D(0,0,0),
,,
则异面直线C1E与BF所成角的余弦值为;
(2)由(1)知,,
设平面ADF的法向量为,
则,
令y=1,则z=﹣3,
∴平面ADF的法向量为,
,,
设平面B1EF的法向量为,
则,令b=1,则c=﹣1,,
∴平面B1EF的法向量为,
平面ADF与平面B1EF所成角的余弦值为.
【点评】本题考查了异面直线所成角和二面角的计算,属于中档题.
18.【分析】(1)直接套公式求出系数r,即可判断;(2)套公式求出回归方程,把x=19代入,即可求解.
【解答】解:(1)由题意可知:,
则,
又,
所以相关系数.
所以y与x的线性相关性较高,可以利用线性回归模型拟合y与x的关系.
(2)由(1)知,,,.
所以,
所以.
所以y与x的回归直线为y=2.5x﹣3.5.
当x=19时,y=2.5×19﹣3.5=44.即在19℃的温度下,种子发芽的颗数为44.
【点评】本题主要考查了相关系数的求解及应用,还考查了线性回归方程的应用,属于中档题.
19.【分析】(1)求导数并求出导数的零点、﹣(a+2),讨论(a+2)的符号,解出导数大于零、小于零或等于零的解,得到原函数的单调区间;
(2)求出导数,然后根据极值点处的导数为0,导数值为﹣2,列出a,b的方程组,最后利用导函数为零所得方程的判别式验证即可.
【解答】解:由题知定义域为R,f′(x)=3x2+2(a+2)x+b,
(1)令f′(x)=3x2+2(a+2)x﹣(a+2)2=0得或﹣(a+2),
①当a+2>0,即a>﹣2时,f′(x)>0 x<﹣(a+2)或x>,f′(x)<0 ﹣(a+2)<x<,
所以f(x)的单调递增区间为(﹣∞,﹣(a+2)),(,+∞);单调递减区间为(﹣(a+2),);
同理得:
②当a+2<0,即a<﹣2时,f(x)的单调递增区间为(﹣(a+2),+∞),(﹣∞,);单调递减区间为(,﹣(a+2));
③当a+2=0,即a=﹣2时,f′(x)≥0恒成立,f(x)是增函数.
(2)由题意得,解得或,
令f′(x)=3x2+2(a+2)x+b=0,
当时,Δ=4(a+2)2﹣12b=36>0,符合题意;
当时,Δ=0,此时f′(x)≥0恒成立,不符合题意,
故a+b=﹣5即为所求.
【点评】本题考查利用导数研究函数单调区间的方法,极值点处性质的应用,属于中档题.
20.【分析】(1)由题意,X可能取1,2,3,计算出各自对应的概率即可求解;
(2)(i)第n次触球者是甲的概率记为Pn,则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,则,化简整理即可得证;
(ii)由(i)知,代入整理即可求解.
【解答】解:(1)由题意,X可能取1,2,3,
则P(X=1)=0.6,P(X=2)=0.4×0.6=0.24,
P(X=3)=0.4×0.4=0.16,
X的分布列为:
X 1 2 3
P 0.6 0.24 0.16
即E(X)=1×0.6+2×0.24+3×0.16=1.56;
(2)证明:(i)第n次触球者是甲的概率记为Pn,则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,
则,
从而,又,
是以为首项,公比为的等比数列;
(ii),,
,
P19>P20,故第19次触球者是甲的概率大.
【点评】本题考查了离散型随机变量的分布列与期望,属于中档题.
21.【分析】(1)设切线切于点P(t,tlnt﹣(a+1)t+1),从而得切线方程为y﹣tlnt+(a+1)t﹣1=(lnt﹣a)(x﹣t),再将(1,1)代入切线方程,最后再根据题意可得关于t的方程有解,从而可得a的范围;
(2)分类讨论a,求出m,n,得到m﹣n,再构造函数求出最小值即可得解.
【解答】解:(1)f(x)的定义域为(0,+∞),f′(x)=lnx+1﹣(a+1)=lnx﹣a,
设切线切于点P(t,tlnt﹣(a+1)t+1),
则切点P处的切线方程为y﹣tlnt+(a+1)t﹣1=(lnt﹣a)(x﹣t),又该切线过(1,1),
∴1﹣tlnt+(a+1)t﹣1=(lnt﹣a)(1﹣t)在t>0上有解,
即a=lnt﹣t在t>0上有解,
设g(x)=lnx﹣x,x>0,,x>0,
∴当x∈(0,1)时,g′(x)>0,g(x)单调递增;
当x∈(1,+∞)时,g′(x)<0,g(x)单调递减,
∴g(x)≤g(1)=﹣1,
∴a=lnt﹣t在t>0上有解,
则a≤﹣1,∴实数a的取值范围为(﹣∞,﹣1];
(2)f′(x)=lnx﹣a,x∈[1,e],lnx∈[0,1],
①当a≥1时,f′(x)≤0恒成立,函数f(x)在区间[1,e]上为减函数,
所以m=f(1)=﹣a,n=f(e)=1﹣ae,所以m﹣n=(e﹣1)a﹣1,
令h(a)=(e﹣1)a﹣1,则函数h(a)在区间[1,+∞)上单调递增,
所以h(a)的最小值为h(1)=e﹣2,即m﹣n的最小值为e﹣2.
②当0<a<1时,由f′(x)>0,得ea<x≤e,由f′(x)<0,得1≤x<ea,
所以f(x)在区间[1,ea)上单调递减,在(ea,e]上单调递增,
所以n=f(ea)=1﹣ea,
当≤a<1时,f(1)﹣f(e)=(e﹣1)a﹣1≥0,此时m=f(1)=﹣a,
所以m﹣n=f(1)﹣f(ea)=ea﹣a﹣1,
令φ(a)=ea﹣a﹣1,φ′(a)=ea﹣1>0,
所以φ(a)在区间[,1)上单调递增,
所以函数φ(a)的最小值为;
当0<a<时,f(1)﹣f(e)=(e﹣1)a﹣1<0,所以m=f(e)=1﹣ae,
所以m﹣n=f(e)﹣f(ea)=ea﹣ae,
令q(a)=ea﹣ae,则q′(a)=ea﹣e<0,
所以函数q(a)在区间(0,)上单调递减,
所以,
综上所述,m﹣n的最小值为.
【点评】本题主要考查方程有解问题,利用导数研究函数的单调性与最值,分类讨论思想,属难题.
22.【分析】(1)构造g(x)=f(x)﹣x=lnx﹣x+a﹣1,利用导数的性质判断g(x)的单调性进行求解即可;
(2)构造,利用导数的性质判断h(x)的单调性,结合函数零点存在原理进行求解即可.
【解答】解:(1)记g(x)=f(x)﹣x=lnx﹣x+a﹣1.
则g(x)≤0恒成立,即g(x)max≤0,
,当x∈(0,1),g'(x)>0;当x∈(1,+∞),g'(x)<0;
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)max=g(1)≤0,解得a≤2.∴实数a的取值范围是(﹣∞,2].
(2)证明:记,
,∵在(0,+∞)上单调递增.
令,,
则,所以φ(x)即h'(x)在(0,+∞)上单调递增.
由a∈(0,1],知,,,,即,
∴当x∈(0,x0),h'(x)<0,h(x)单调递减;当x∈(x0,+∞),h'(x)>0,h(x)单调递增,
,
由(*)式,可得,,
代入(**)式,得,
由(1)知,当a=2时有lnx≤x﹣1,
故﹣lnx0≥1﹣x0.,
由,∴h(x0)≥0,
故h(x)≥0,即,原不等式得证.
【点评】本题主要考查利用导数研究函数的单调性与最值,考查不等式的证明,考查运算求解能力与逻辑推理能力,属于难题.
同课章节目录
