黑龙江省嫩江县第一中学高中数学人教选修4-1 24 弦切角的性质 导学案 (无答案)
文档属性
| 名称 | 黑龙江省嫩江县第一中学高中数学人教选修4-1 24 弦切角的性质 导学案 (无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 16.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-18 20:22:41 | ||
图片预览

文档简介
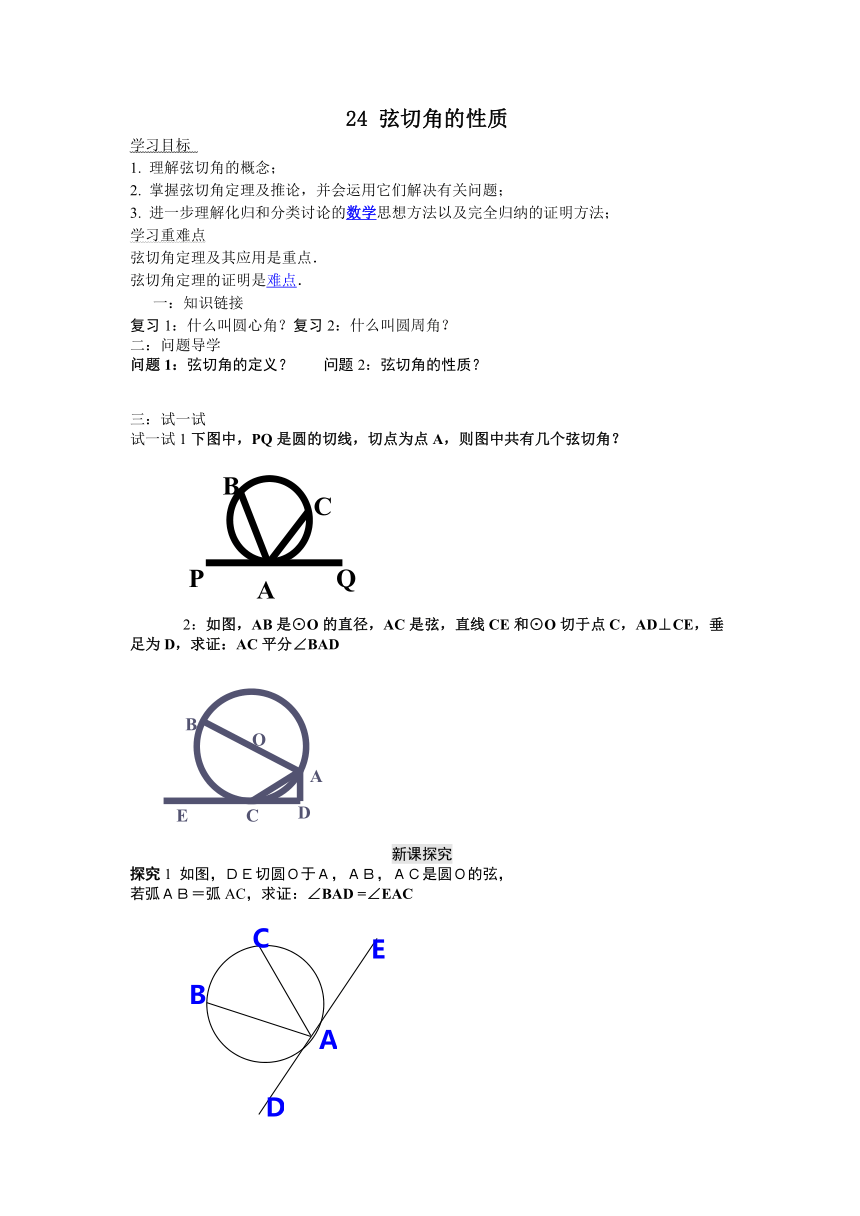
24 弦切角的性质
学习目标
1. 理解弦切角的概念;
2. 掌握弦切角定理及推论,并会运用它们解决有关问题;
3. 进一步理解化归和分类讨论的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想方法以及完全归纳的证明方法;
学习重难点
弦切角定理及其应用是重点.
弦切角定理的证明是难点 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ).
一:知识链接
复习1:什么叫圆心角?复习2:什么叫圆周角?
二:问题导学
问题1:弦切角的定义? 问题2:弦切角的性质?
三:试一试
试一试1下图中,PQ是圆的切线,切点为点A,则图中共有几个弦切角?
2:如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D,求证:AC平分∠BAD
新课探究
探究1 如图,DE切圆O于A,AB,AC是圆O的弦,
若弧AB=弧AC,求证:∠BAD =∠EAC
探究2如图AB为圆O的直径,弦CD∥AB,AE切圆O于A,交CD的延长线于E,求证:BC =AB*DE
模仿练习
练1. 如图:点D是⊙O的半径OA上一点,经过点D作弦BC⊥AO,过C引⊙O的切线与OA的延长线交于点E.求证:CA平分∠BCE
练2. 已知:BC与⊙O相切于点B,AF为⊙O的直径, CE⊥AF,垂足为E,求证:CD=CB
Q
P
C
B
A
·
A
D
C
E
B
O
A
B
C
D
E
D
C
E
B
A
C
E
B
O
A
D
C
E
B
O
A
D
A
C
D
E
O
F
B
学习目标
1. 理解弦切角的概念;
2. 掌握弦切角定理及推论,并会运用它们解决有关问题;
3. 进一步理解化归和分类讨论的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想方法以及完全归纳的证明方法;
学习重难点
弦切角定理及其应用是重点.
弦切角定理的证明是难点 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank ).
一:知识链接
复习1:什么叫圆心角?复习2:什么叫圆周角?
二:问题导学
问题1:弦切角的定义? 问题2:弦切角的性质?
三:试一试
试一试1下图中,PQ是圆的切线,切点为点A,则图中共有几个弦切角?
2:如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D,求证:AC平分∠BAD
新课探究
探究1 如图,DE切圆O于A,AB,AC是圆O的弦,
若弧AB=弧AC,求证:∠BAD =∠EAC
探究2如图AB为圆O的直径,弦CD∥AB,AE切圆O于A,交CD的延长线于E,求证:BC =AB*DE
模仿练习
练1. 如图:点D是⊙O的半径OA上一点,经过点D作弦BC⊥AO,过C引⊙O的切线与OA的延长线交于点E.求证:CA平分∠BCE
练2. 已知:BC与⊙O相切于点B,AF为⊙O的直径, CE⊥AF,垂足为E,求证:CD=CB
Q
P
C
B
A
·
A
D
C
E
B
O
A
B
C
D
E
D
C
E
B
A
C
E
B
O
A
D
C
E
B
O
A
D
A
C
D
E
O
F
B
