第1单元圆柱与圆锥能力提升卷-数学六年级下册北师大版(含答案)
文档属性
| 名称 | 第1单元圆柱与圆锥能力提升卷-数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 429.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 21:51:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1单元圆柱与圆锥能力提升卷-数学六年级下册北师大版
一、选择题
1.在下图中,以直线为轴旋转,可以得到圆柱体的是( )
A. B. C. D.
2.圆锥的底面积是16平方厘米,高6厘米,它的体积是( )。
A.96立方厘米 B.23立方厘米 C.69立方厘米 D.32立方厘米
3.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面( )圆形铁片正好可以做成圆柱形容器。
A.无法计算 B.d=3厘米
C.r=4厘米 D.d=6厘米或8厘米
4.把一块高6cm的圆柱形橡皮泥捏成与它等底,高是3cm的圆锥形橡皮泥,可捏( )个。
A.3 B.6 C.9 D.12
5.把一个棱长为6cm的正方体铁块削成一个最大的圆柱形零件,这个零件的体积是( )。
A.56.52cm3 B.169.56cm3 C.678.24cm3 D.113.04cm3
6.一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的,它的体积( )。
A.扩大到原来的2倍 B.缩小到原来的
C.缩小到原来的 D.大小不变
二、填空题
7.一个圆锥的底面半径是2厘米,高是0.6分米,它的体积是( )立方厘米。
8.制作一节长2米,底面直径0.2米的圆柱形通风管,至少需要铁皮( )平方米。
9.一个圆柱和一个圆锥的体积相等,底面积也相等,圆柱的高是1.2米,圆锥的高是( )米。
10.笑笑到自己家开的小超市帮忙。他把8个同样的圆柱形玻璃杯,按照如图所示的方式紧密地放入纸盒中。这个纸盒的长是( )cm,宽是( )cm,高是( )cm。
11.如图,将长方形绕直线a旋转一周,能形成一个圆柱,这个圆柱的表面积是( )cm2,体积是( )cm3。
12.一个圆柱形木块体积是180立方厘米,把它削成一个最大的圆锥,圆锥的体积是( )立方厘米。
三、判断题
13.圆锥由两个底面和一个侧面组成。( )
14.侧面积相等的两个圆柱,表面积不一定相等。( )
15.一枚硬币厚2毫米,将10枚这样的硬币摞成一个圆柱,这个圆柱的高是20厘米。( )
16.将一个实心圆柱锻造成一个底面积与它相等的实心圆锥,这个实心圆锥的高是这个圆柱的3倍。( )
17.如果一个圆柱与一个圆锥等底等体积,那么圆柱与圆锥高的比是1∶3。( )
四、计算题
18.计算体积。
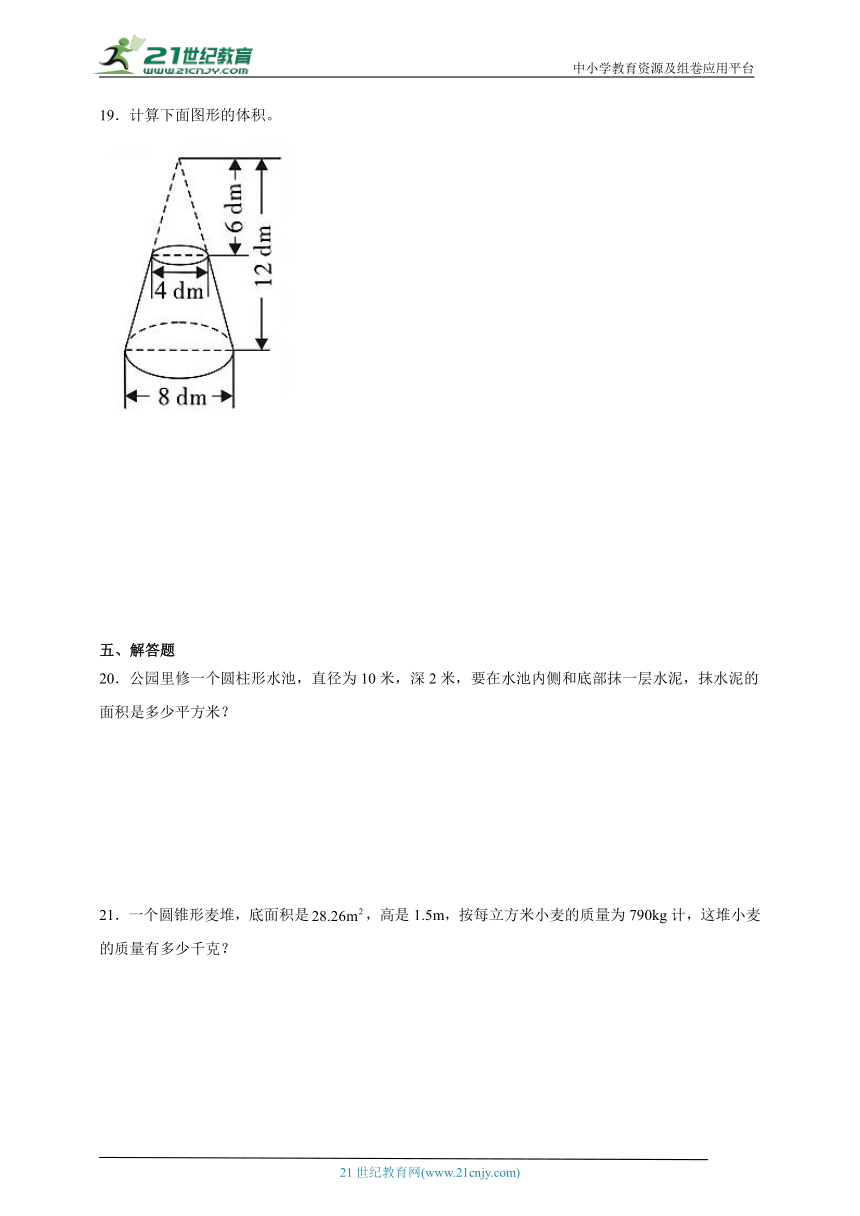
19.计算下面图形的体积。
五、解答题
20.公园里修一个圆柱形水池,直径为10米,深2米,要在水池内侧和底部抹一层水泥,抹水泥的面积是多少平方米?
21.一个圆锥形麦堆,底面积是,高是1.5m,按每立方米小麦的质量为790kg计,这堆小麦的质量有多少千克?
22.如图是一个贮存小麦的粮仓,上面是圆锥形,下面是圆柱形,忽略粮仓的厚度,这个粮仓的容积大约是多少立方米?
23.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
24.如图,有一个下面是圆锥、上面是圆柱的容器,圆锥的高是6cm,圆柱的高是8cm,从圆锥的尖到容器里的液面高是11cm。当将这个容器倒过来放平时,容器里的液面高是多少厘米?
参考答案:
1.C
【详解】根据各图形的特征,长方形绕一边所在的直线为轴旋转一周得到到一个圆柱;
故选:C.
2.D
【解析】圆锥的体积=底面积×高×,由此根据圆锥的体积公式列式计算即可。
【详解】16×6×
=16×2
=32(立方厘米)
故答案为:D
【点睛】此题主要考查圆锥的体积公式,注意不要忘记乘,在理解的基础上记忆。
3.D
【解析】所配的圆形铁片的周长等于长方形铁皮的长或宽即可做成圆柱形容器。
【详解】25.12÷3.14=8(厘米),
18.84÷3.14=6(厘米),
答:可以配上直径6厘米或8厘米的圆形铁片正好做成圆柱形容器。
故选:D。
【点睛】长方形铁皮是圆柱体的侧面,其长或宽都可以做圆柱体的底面周长,注意不要漏掉其中任何一种情况。
4.B
【解析】等底等高的圆柱和圆锥,圆柱体积是圆锥3倍,先想高6厘米的圆柱可以分成两个高3厘米的圆柱,每个高3厘米的圆柱都可以捏成3个高3厘米的圆锥。
【详解】6÷3×3=6(个)
故答案为:B
【点睛】本题考查了圆柱和圆锥的体积,要灵活运用方法。
5.B
【解析】正方体的棱长是削成的最大圆柱的底面直径和高,据此根据圆柱的体积公式计算即可。
【详解】6÷2=3(厘米)
3.14×3×6=169.56(立方厘米)
故答案为:B
【点睛】本题考查了圆柱的体积,圆柱体积=底面积×高。
6.B
【解析】因为圆柱的体积=底面积×高,底面周长缩小到原来的,所以底面积缩小为原来的,高扩大到原来的2倍,所以圆柱的体积缩小到原来的。
【详解】一个圆柱的高扩大到原来的2倍,底面积缩小为原来的,所以它的体积缩小到原来的。
故答案为:B
【点睛】注意周长缩小到原来的,那么半径缩小到原来的,因为圆的面积=π×r×r,所以面积缩小为原来的。
7.25.12
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】0.6分米=6厘米
×3.14×22×6
=3.14×4×2
=25.12(立方厘米)
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
8.1.256
【分析】根据圆柱的侧面积公式:S=πdh,代入计算即可求得需要白铁皮的面积。
【详解】3.14×0.2×2
=0.628×2
=1.256平方米
【点睛】本题的关键是理解圆柱形铁皮通风管需要铁皮的面积=圆柱形铁皮通风管的侧面积。
9.3.6
【分析】在等底、等体积时,已知圆柱的高是1.2米,所以圆锥的高是圆柱的3倍。
【详解】1.2×3=3.6(米)
【点睛】关键是理解圆柱和圆锥体积之间的关系。
10. 24 12 10
【分析】从图中可知:长方形纸盒中紧密放入8个同样的圆柱形玻璃杯,长方形纸盒的长为4个圆柱形玻璃杯的直径的和,长方形纸盒的宽为2个圆柱形玻璃杯的直径的和,长方形纸盒的高为圆柱形玻璃杯的高,据此可算出长方形纸盒的长、宽、高。
【详解】长方形纸盒的长:4×6=24cm
长方形纸盒的宽:2×6=12cm
长方形纸盒的高=圆柱形玻璃杯的高=10cm
【点睛】此题主要考查长方体和圆柱的体积关系,若干个圆柱体的体积的和通过等积变形可得到长方体的体积。
11. 87.92 62.8
【分析】根据题意可知,圆柱的底面半径是2厘米,高是5厘米,根据圆柱的表面积S=2πr2+πdh,圆柱的体积=πr2h,代入数据计算即可。
【详解】表面积:3.14×22×2+2×3.14×2×5
=3.14×8+3.14×20
=3.14×28
=87.92(平方厘米);
体积:3.14×22×5
=3.14×20
=62.8(立方厘米)
【点睛】此题考查了圆柱的表面积、体积的计算,找出圆柱的底面半径和高是解题关键。
12.60
【分析】如果把圆柱削成一个最大的圆锥,那么圆锥与圆柱就等底等高,圆锥的体积是圆柱体积的;据此解答。
【详解】180×=60(立方厘米)
【点睛】此题主要考查学生对等底等高的圆柱和圆锥的体积之间的关系的理解与应用,需要理解把圆柱削成一个最大的圆锥,那么圆锥与圆柱就等底等高。
13.×
【分析】
根据圆锥的特征可知,圆锥有一个底面、一个侧面。圆锥的侧面是一个曲面,展开后是一个扇形,据此判断即可。
【详解】
圆锥由两个底面和一个侧面组成。所以原题说法是错误的。
故答案为:×
14.√
【分析】
圆柱的侧面积=(r是半径,h是高),圆柱的表面积=侧面积+2个底面积。侧面积相等的两个圆柱的底面半径和高也不一定相等,则底面积也不一定相等,所以表面积不一定相等。
【详解】面积相等的两个圆柱,半径不一定相等,则表面积不一定相等。
故答案为:√
15.×
【分析】根据题意,用一枚硬币的厚度乘10,即是10枚这样的硬币摞成圆柱的高度,计算结果根据进率“1厘米=10毫米”换算单位即可。
【详解】2×10=20(毫米)
20毫米=2厘米
这个圆柱的高是2厘米。
原题说法错误。
故答案为:×
16.√
【分析】锻造前后体积不变,圆柱的体积公式为:V=Sh,圆锥的体积公式为V=Sh,设圆柱的体积为V,底面积为S,则圆锥的体积为V,底面积是S,由此分别表示出圆柱、圆锥的高,进而得出圆锥高是圆柱高的几倍;据此解答。
【详解】假设圆柱的体积为V,底面积为S,则圆锥的体积为V,底面积是S;
圆柱的高为:h圆柱=
圆锥的高为:h圆锥=
圆锥的高是圆柱高的÷=×=3倍,原说法正确。
故答案为:√
【点睛】等底等高的圆柱的体积是圆锥体积的3倍,等积等底的圆锥的高是圆柱高的3倍。
17.√
【分析】根据圆柱的体积公式,V=Sh,与圆锥的体积公式,V=Sh,知道在底面积和体积分别相等时,圆柱的高是圆锥的高的,由此做出判断。
【详解】圆柱的体积是:V=Sh1
圆锥的体积是:V=Sh2
体积相等则Sh1=Sh2
h1=h2
即h1∶h2=1∶3
所以圆柱与圆锥高的比是1∶3,题干说法正确。
故答案为:√
【点睛】此题主要是利用圆柱与圆锥的体积公式,推导出在底面积和体积分别相等时,圆柱的高与圆锥的高的关系。
18.1.57立方厘米
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】3.14×(1÷2)2×2
=3.14×0.25×2
=1.57(立方厘米)
19.175.84dm3
【分析】根据圆锥的体积公式,用底面直径为8dm,高为12dm的圆锥的体积减去底面直径为4dm,高为6dm的圆锥的体积,根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】×3.14×(8÷2)2×12-×3.14×(4÷2)2×6
=×3.14×16×12-×3.14×4×6
=200.96-25.12
=175.84(dm3)
20.141.3平方米
【分析】求抹水泥的面积是多少平方米,首先分清需要计算圆柱形水池几个面的面积,是求一个侧面积与一个底面积的和,由圆柱体侧面积和圆的面积计算方法列式解答即可。
【详解】3.14×(10÷2)2+3.14×10×2
=3.14×25+3.14×20
=3.14×45
=141.3(平方米)
答:抹水泥的面积是141.3平方米。
【点睛】解答此题主要分清所求物体的形状,把问题转换为是求圆柱的表面积,把实际问题转化为数学问题,再运用数学知识解决。
21.11162.7千克
【分析】根据题意,这是圆锥形麦堆,已知圆锥的底面积、高,根据圆锥的体积公式:底面×高×,即:28.26×1.5×,计算出圆锥的体积,每立方米小麦的质量是790,这堆小麦的质量就用圆锥的体积×790,即:28.26×1.5××790,即可解答。
【详解】28.26×1.5××790
=42.39××790
=14.13×790
=11162.7(千克)
答:这对小面的质量有11162.7千克。
【点睛】本题考查圆锥体的体积公式的实际运用,注意计算时要细心。
22.5.652立方米
【分析】根据圆锥的体积V= πr2h,圆柱的体积V= πr2h,代入数据计算它们的体积,相加即可。
【详解】2÷2=1(米)
×3.14×12×0.9+3.14×12×1.5
=0.942+4.71
=5.652(立方米)
答:这个粮仓的容积大约是5.652立方米。
【点睛】此题考查了圆锥、圆柱体积的公式的灵活运用,牢记公式认真计算即可。
23.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
24.7厘米
【分析】根据等底等高的圆柱的体积是圆锥的体积的3倍,所以先把圆锥内6厘米深的水倒入圆柱中,即为高6÷3=2厘米的水的体积,原来圆柱内水的高度为11-6=5厘米,当将这个容器倒过来放平时,容器里的液面高是5+2=7(厘米)。据此解答。
【详解】6÷3+(11-6)
=2+5
=7(厘米)
答:容器里的液面高是7厘米。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用,这里关键是找出圆锥内高6厘米的水的是指在圆柱内高度为2厘米的水的体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元圆柱与圆锥能力提升卷-数学六年级下册北师大版
一、选择题
1.在下图中,以直线为轴旋转,可以得到圆柱体的是( )
A. B. C. D.
2.圆锥的底面积是16平方厘米,高6厘米,它的体积是( )。
A.96立方厘米 B.23立方厘米 C.69立方厘米 D.32立方厘米
3.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面( )圆形铁片正好可以做成圆柱形容器。
A.无法计算 B.d=3厘米
C.r=4厘米 D.d=6厘米或8厘米
4.把一块高6cm的圆柱形橡皮泥捏成与它等底,高是3cm的圆锥形橡皮泥,可捏( )个。
A.3 B.6 C.9 D.12
5.把一个棱长为6cm的正方体铁块削成一个最大的圆柱形零件,这个零件的体积是( )。
A.56.52cm3 B.169.56cm3 C.678.24cm3 D.113.04cm3
6.一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的,它的体积( )。
A.扩大到原来的2倍 B.缩小到原来的
C.缩小到原来的 D.大小不变
二、填空题
7.一个圆锥的底面半径是2厘米,高是0.6分米,它的体积是( )立方厘米。
8.制作一节长2米,底面直径0.2米的圆柱形通风管,至少需要铁皮( )平方米。
9.一个圆柱和一个圆锥的体积相等,底面积也相等,圆柱的高是1.2米,圆锥的高是( )米。
10.笑笑到自己家开的小超市帮忙。他把8个同样的圆柱形玻璃杯,按照如图所示的方式紧密地放入纸盒中。这个纸盒的长是( )cm,宽是( )cm,高是( )cm。
11.如图,将长方形绕直线a旋转一周,能形成一个圆柱,这个圆柱的表面积是( )cm2,体积是( )cm3。
12.一个圆柱形木块体积是180立方厘米,把它削成一个最大的圆锥,圆锥的体积是( )立方厘米。
三、判断题
13.圆锥由两个底面和一个侧面组成。( )
14.侧面积相等的两个圆柱,表面积不一定相等。( )
15.一枚硬币厚2毫米,将10枚这样的硬币摞成一个圆柱,这个圆柱的高是20厘米。( )
16.将一个实心圆柱锻造成一个底面积与它相等的实心圆锥,这个实心圆锥的高是这个圆柱的3倍。( )
17.如果一个圆柱与一个圆锥等底等体积,那么圆柱与圆锥高的比是1∶3。( )
四、计算题
18.计算体积。
19.计算下面图形的体积。
五、解答题
20.公园里修一个圆柱形水池,直径为10米,深2米,要在水池内侧和底部抹一层水泥,抹水泥的面积是多少平方米?
21.一个圆锥形麦堆,底面积是,高是1.5m,按每立方米小麦的质量为790kg计,这堆小麦的质量有多少千克?
22.如图是一个贮存小麦的粮仓,上面是圆锥形,下面是圆柱形,忽略粮仓的厚度,这个粮仓的容积大约是多少立方米?
23.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
24.如图,有一个下面是圆锥、上面是圆柱的容器,圆锥的高是6cm,圆柱的高是8cm,从圆锥的尖到容器里的液面高是11cm。当将这个容器倒过来放平时,容器里的液面高是多少厘米?
参考答案:
1.C
【详解】根据各图形的特征,长方形绕一边所在的直线为轴旋转一周得到到一个圆柱;
故选:C.
2.D
【解析】圆锥的体积=底面积×高×,由此根据圆锥的体积公式列式计算即可。
【详解】16×6×
=16×2
=32(立方厘米)
故答案为:D
【点睛】此题主要考查圆锥的体积公式,注意不要忘记乘,在理解的基础上记忆。
3.D
【解析】所配的圆形铁片的周长等于长方形铁皮的长或宽即可做成圆柱形容器。
【详解】25.12÷3.14=8(厘米),
18.84÷3.14=6(厘米),
答:可以配上直径6厘米或8厘米的圆形铁片正好做成圆柱形容器。
故选:D。
【点睛】长方形铁皮是圆柱体的侧面,其长或宽都可以做圆柱体的底面周长,注意不要漏掉其中任何一种情况。
4.B
【解析】等底等高的圆柱和圆锥,圆柱体积是圆锥3倍,先想高6厘米的圆柱可以分成两个高3厘米的圆柱,每个高3厘米的圆柱都可以捏成3个高3厘米的圆锥。
【详解】6÷3×3=6(个)
故答案为:B
【点睛】本题考查了圆柱和圆锥的体积,要灵活运用方法。
5.B
【解析】正方体的棱长是削成的最大圆柱的底面直径和高,据此根据圆柱的体积公式计算即可。
【详解】6÷2=3(厘米)
3.14×3×6=169.56(立方厘米)
故答案为:B
【点睛】本题考查了圆柱的体积,圆柱体积=底面积×高。
6.B
【解析】因为圆柱的体积=底面积×高,底面周长缩小到原来的,所以底面积缩小为原来的,高扩大到原来的2倍,所以圆柱的体积缩小到原来的。
【详解】一个圆柱的高扩大到原来的2倍,底面积缩小为原来的,所以它的体积缩小到原来的。
故答案为:B
【点睛】注意周长缩小到原来的,那么半径缩小到原来的,因为圆的面积=π×r×r,所以面积缩小为原来的。
7.25.12
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】0.6分米=6厘米
×3.14×22×6
=3.14×4×2
=25.12(立方厘米)
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
8.1.256
【分析】根据圆柱的侧面积公式:S=πdh,代入计算即可求得需要白铁皮的面积。
【详解】3.14×0.2×2
=0.628×2
=1.256平方米
【点睛】本题的关键是理解圆柱形铁皮通风管需要铁皮的面积=圆柱形铁皮通风管的侧面积。
9.3.6
【分析】在等底、等体积时,已知圆柱的高是1.2米,所以圆锥的高是圆柱的3倍。
【详解】1.2×3=3.6(米)
【点睛】关键是理解圆柱和圆锥体积之间的关系。
10. 24 12 10
【分析】从图中可知:长方形纸盒中紧密放入8个同样的圆柱形玻璃杯,长方形纸盒的长为4个圆柱形玻璃杯的直径的和,长方形纸盒的宽为2个圆柱形玻璃杯的直径的和,长方形纸盒的高为圆柱形玻璃杯的高,据此可算出长方形纸盒的长、宽、高。
【详解】长方形纸盒的长:4×6=24cm
长方形纸盒的宽:2×6=12cm
长方形纸盒的高=圆柱形玻璃杯的高=10cm
【点睛】此题主要考查长方体和圆柱的体积关系,若干个圆柱体的体积的和通过等积变形可得到长方体的体积。
11. 87.92 62.8
【分析】根据题意可知,圆柱的底面半径是2厘米,高是5厘米,根据圆柱的表面积S=2πr2+πdh,圆柱的体积=πr2h,代入数据计算即可。
【详解】表面积:3.14×22×2+2×3.14×2×5
=3.14×8+3.14×20
=3.14×28
=87.92(平方厘米);
体积:3.14×22×5
=3.14×20
=62.8(立方厘米)
【点睛】此题考查了圆柱的表面积、体积的计算,找出圆柱的底面半径和高是解题关键。
12.60
【分析】如果把圆柱削成一个最大的圆锥,那么圆锥与圆柱就等底等高,圆锥的体积是圆柱体积的;据此解答。
【详解】180×=60(立方厘米)
【点睛】此题主要考查学生对等底等高的圆柱和圆锥的体积之间的关系的理解与应用,需要理解把圆柱削成一个最大的圆锥,那么圆锥与圆柱就等底等高。
13.×
【分析】
根据圆锥的特征可知,圆锥有一个底面、一个侧面。圆锥的侧面是一个曲面,展开后是一个扇形,据此判断即可。
【详解】
圆锥由两个底面和一个侧面组成。所以原题说法是错误的。
故答案为:×
14.√
【分析】
圆柱的侧面积=(r是半径,h是高),圆柱的表面积=侧面积+2个底面积。侧面积相等的两个圆柱的底面半径和高也不一定相等,则底面积也不一定相等,所以表面积不一定相等。
【详解】面积相等的两个圆柱,半径不一定相等,则表面积不一定相等。
故答案为:√
15.×
【分析】根据题意,用一枚硬币的厚度乘10,即是10枚这样的硬币摞成圆柱的高度,计算结果根据进率“1厘米=10毫米”换算单位即可。
【详解】2×10=20(毫米)
20毫米=2厘米
这个圆柱的高是2厘米。
原题说法错误。
故答案为:×
16.√
【分析】锻造前后体积不变,圆柱的体积公式为:V=Sh,圆锥的体积公式为V=Sh,设圆柱的体积为V,底面积为S,则圆锥的体积为V,底面积是S,由此分别表示出圆柱、圆锥的高,进而得出圆锥高是圆柱高的几倍;据此解答。
【详解】假设圆柱的体积为V,底面积为S,则圆锥的体积为V,底面积是S;
圆柱的高为:h圆柱=
圆锥的高为:h圆锥=
圆锥的高是圆柱高的÷=×=3倍,原说法正确。
故答案为:√
【点睛】等底等高的圆柱的体积是圆锥体积的3倍,等积等底的圆锥的高是圆柱高的3倍。
17.√
【分析】根据圆柱的体积公式,V=Sh,与圆锥的体积公式,V=Sh,知道在底面积和体积分别相等时,圆柱的高是圆锥的高的,由此做出判断。
【详解】圆柱的体积是:V=Sh1
圆锥的体积是:V=Sh2
体积相等则Sh1=Sh2
h1=h2
即h1∶h2=1∶3
所以圆柱与圆锥高的比是1∶3,题干说法正确。
故答案为:√
【点睛】此题主要是利用圆柱与圆锥的体积公式,推导出在底面积和体积分别相等时,圆柱的高与圆锥的高的关系。
18.1.57立方厘米
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】3.14×(1÷2)2×2
=3.14×0.25×2
=1.57(立方厘米)
19.175.84dm3
【分析】根据圆锥的体积公式,用底面直径为8dm,高为12dm的圆锥的体积减去底面直径为4dm,高为6dm的圆锥的体积,根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】×3.14×(8÷2)2×12-×3.14×(4÷2)2×6
=×3.14×16×12-×3.14×4×6
=200.96-25.12
=175.84(dm3)
20.141.3平方米
【分析】求抹水泥的面积是多少平方米,首先分清需要计算圆柱形水池几个面的面积,是求一个侧面积与一个底面积的和,由圆柱体侧面积和圆的面积计算方法列式解答即可。
【详解】3.14×(10÷2)2+3.14×10×2
=3.14×25+3.14×20
=3.14×45
=141.3(平方米)
答:抹水泥的面积是141.3平方米。
【点睛】解答此题主要分清所求物体的形状,把问题转换为是求圆柱的表面积,把实际问题转化为数学问题,再运用数学知识解决。
21.11162.7千克
【分析】根据题意,这是圆锥形麦堆,已知圆锥的底面积、高,根据圆锥的体积公式:底面×高×,即:28.26×1.5×,计算出圆锥的体积,每立方米小麦的质量是790,这堆小麦的质量就用圆锥的体积×790,即:28.26×1.5××790,即可解答。
【详解】28.26×1.5××790
=42.39××790
=14.13×790
=11162.7(千克)
答:这对小面的质量有11162.7千克。
【点睛】本题考查圆锥体的体积公式的实际运用,注意计算时要细心。
22.5.652立方米
【分析】根据圆锥的体积V= πr2h,圆柱的体积V= πr2h,代入数据计算它们的体积,相加即可。
【详解】2÷2=1(米)
×3.14×12×0.9+3.14×12×1.5
=0.942+4.71
=5.652(立方米)
答:这个粮仓的容积大约是5.652立方米。
【点睛】此题考查了圆锥、圆柱体积的公式的灵活运用,牢记公式认真计算即可。
23.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
24.7厘米
【分析】根据等底等高的圆柱的体积是圆锥的体积的3倍,所以先把圆锥内6厘米深的水倒入圆柱中,即为高6÷3=2厘米的水的体积,原来圆柱内水的高度为11-6=5厘米,当将这个容器倒过来放平时,容器里的液面高是5+2=7(厘米)。据此解答。
【详解】6÷3+(11-6)
=2+5
=7(厘米)
答:容器里的液面高是7厘米。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用,这里关键是找出圆锥内高6厘米的水的是指在圆柱内高度为2厘米的水的体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
