椭圆的几何性质(广东省广州市花都区)
文档属性
| 名称 | 椭圆的几何性质(广东省广州市花都区) |

|
|
| 格式 | rar | ||
| 文件大小 | 123.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 00:00:00 | ||
图片预览



文档简介
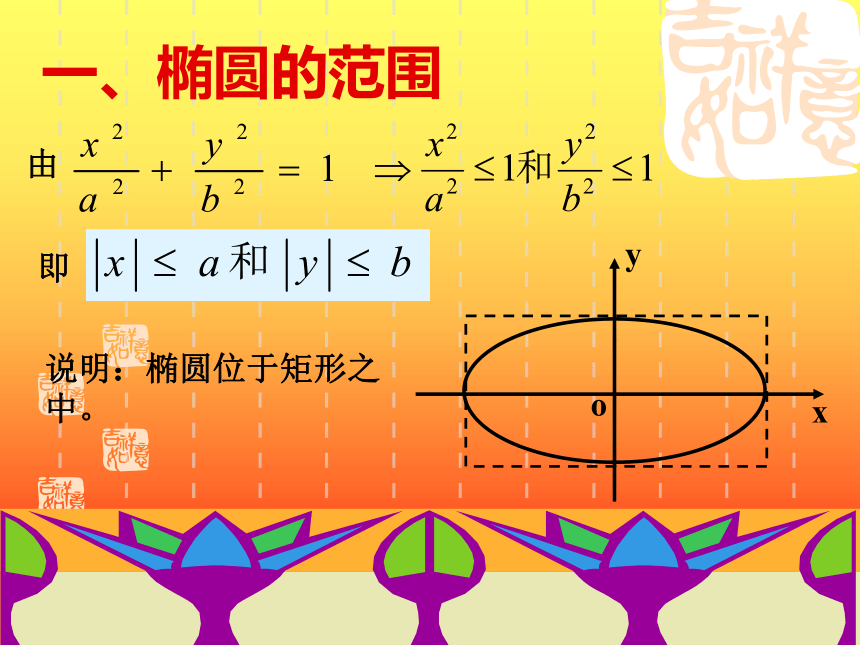
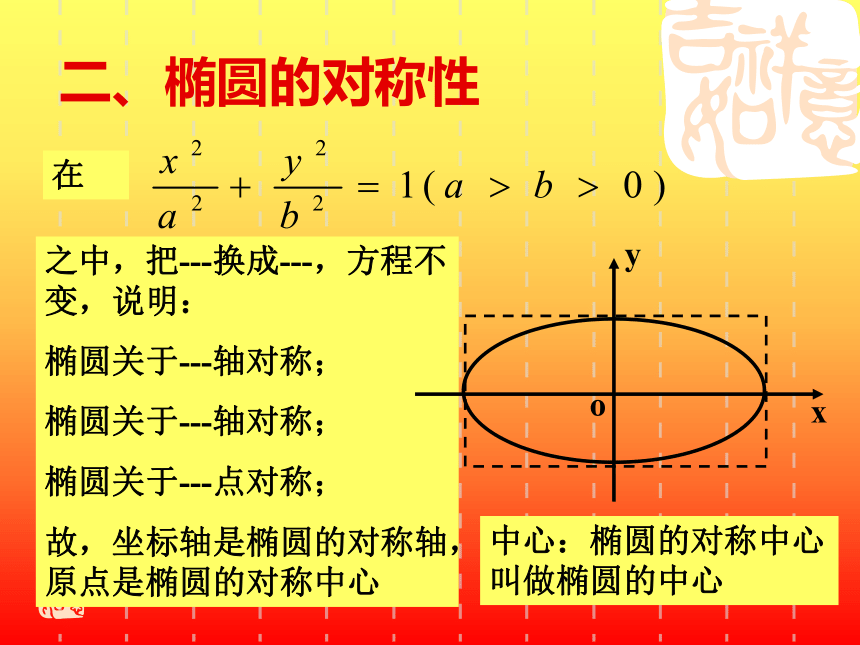
课件14张PPT。椭圆的几何性质(1)复习:1.椭圆的定义:在同一平面内,到两定点F1、F2的距离和为常数(大于|F1F2 |)的点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2一、椭圆的范围由即说明:椭圆位于矩形之中。二、椭圆的对称性在之中,把---换成---,方程不变,说明:
椭圆关于---轴对称;
椭圆关于---轴对称;
椭圆关于---点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
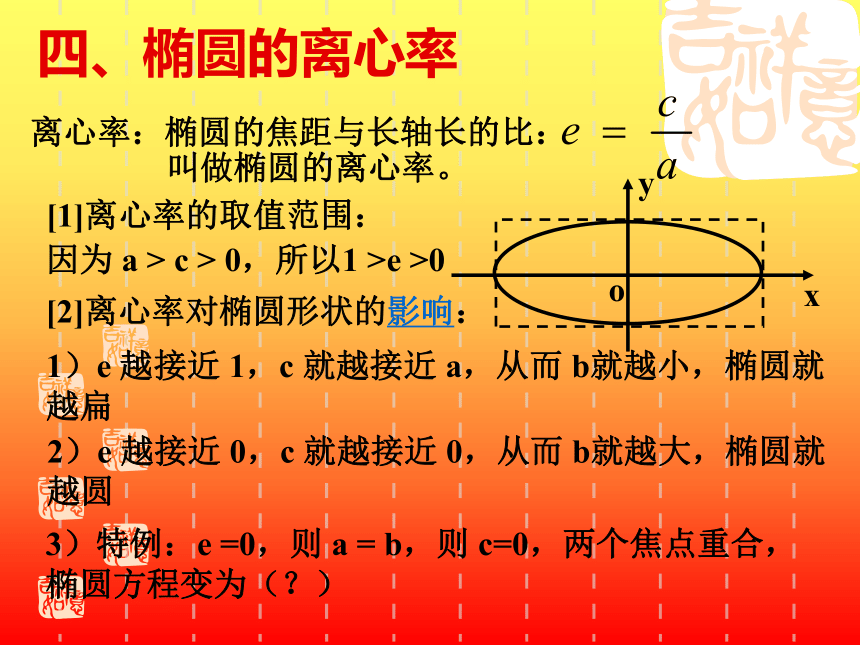
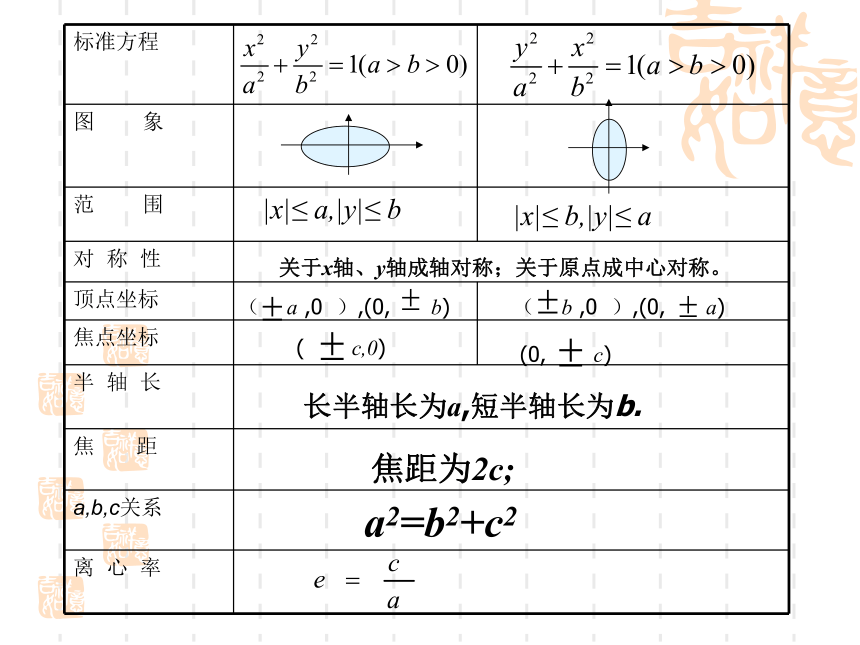
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c,0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1已知椭圆方程为16x2+25y2=400,并用 描点法画出它的图形. 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: __。
外切矩形的面积等于: 。 108680例2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。答案:分类讨论的数学思想课堂练习: 1.已知椭圆的一个焦点将长轴分为 两段,求其离心率解:由题意,,即解得 2.如图,求椭圆 内接正方形ABCD的面积解 由椭圆和正方形的中心对称性知,正方形BFOE的面积是所求
正方形面积的1/4,且B点横纵坐标相等,故设B(t,t)代入椭圆方程
求得
即正方形ABCD面积为练习3:已知椭圆的方程为x2+a2y2=a2 (a>0且 )它的长轴长是: ;
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ;
顶点坐标是: ;
外切矩形的面积等于: ; 当a>1时:
。
。
。
。
。
。
。
当0
椭圆关于---轴对称;
椭圆关于---轴对称;
椭圆关于---点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c,0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1已知椭圆方程为16x2+25y2=400,并用 描点法画出它的图形. 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: __。
外切矩形的面积等于: 。 108680例2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。答案:分类讨论的数学思想课堂练习: 1.已知椭圆的一个焦点将长轴分为 两段,求其离心率解:由题意,,即解得 2.如图,求椭圆 内接正方形ABCD的面积解 由椭圆和正方形的中心对称性知,正方形BFOE的面积是所求
正方形面积的1/4,且B点横纵坐标相等,故设B(t,t)代入椭圆方程
求得
即正方形ABCD面积为练习3:已知椭圆的方程为x2+a2y2=a2 (a>0且 )它的长轴长是: ;
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ;
顶点坐标是: ;
外切矩形的面积等于: ; 当a>1时:
。
。
。
。
。
。
。
当0
