曲线与方程(广东省广州市花都区)
文档属性
| 名称 | 曲线与方程(广东省广州市花都区) |

|
|
| 格式 | rar | ||
| 文件大小 | 272.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 00:00:00 | ||
图片预览








文档简介
课件22张PPT。曲线和方程2019-3-13画一画:1.第一、三象限夹角平分线
2.画出以(0,0)为圆心,1为半径的圆C2019-3-13
(1)观察直线 上的点满足怎样的条件?直线 上的点的坐标满足怎样的方程?直线 与方程有怎样的关系?点的横坐标与纵坐标相等x=y(或x-y=0)得出关系:曲线条件方程探究1:2019-3-13满足关系:·2019-3-13教师总结:
由探索1可知,在直角坐标系建立以后,平面内的点与数对(x,y)建立了一一对应关系。点的运动形成曲线C,与之对应的实数对的变化就形成了方程F(x,y)=0 。
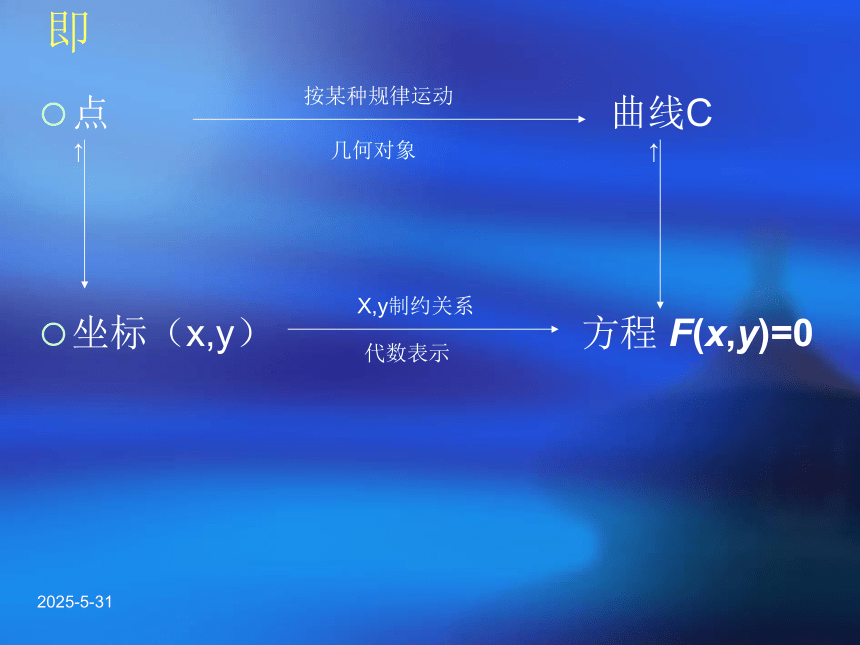
2019-3-13即点 曲线C
坐标(x,y) 方程 F(x,y)=0 按某种规律运动几何对象2019-3-13探究2:(1)2019-3-132019-3-13由探究2可知:改变曲线,方程中的任何一个,曲线和方程就不满足一一对应关系。2019-3-13探究3在直角坐标系中曲线C上的点与方程F(x,y)=0 的解一一对应的条件是什么?2019-3-13给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线上的点坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么这个方程f(x,y)=0叫做这条曲线C的方程
这条曲线C叫做这个方程的曲线定义分析特例归纳定义曲线的方程,方程的曲线2019-3-132、两者间的关系:点在曲线上即:曲线上所有点的集合与此曲线的方程的解集能够一一对应分析特例归纳定义2019-3-13例1判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错学习例题巩固定义2019-3-132019-3-132019-3-132019-3-13第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:证明已知曲线的方程的方法和步骤第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.2019-3-13做一做2019-3-132019-3-13在轨迹的基础上将轨迹和条件化为曲线和方程,当说某方程是曲线的方程或某曲线是方程的曲线时就意味着具备上述两个条件,只有具备上述两个方面的要求,才能将曲线的研究化为方程的研究,几何问题化为代数问题,以数助形正是解析几何的思想,本节课正是这一思想的基础。小结:2019-3-13习题2.1A组1题 优化设计2019-3-13
2.画出以(0,0)为圆心,1为半径的圆C2019-3-13
(1)观察直线 上的点满足怎样的条件?直线 上的点的坐标满足怎样的方程?直线 与方程有怎样的关系?点的横坐标与纵坐标相等x=y(或x-y=0)得出关系:曲线条件方程探究1:2019-3-13满足关系:·2019-3-13教师总结:
由探索1可知,在直角坐标系建立以后,平面内的点与数对(x,y)建立了一一对应关系。点的运动形成曲线C,与之对应的实数对的变化就形成了方程F(x,y)=0 。
2019-3-13即点 曲线C
坐标(x,y) 方程 F(x,y)=0 按某种规律运动几何对象2019-3-13探究2:(1)2019-3-132019-3-13由探究2可知:改变曲线,方程中的任何一个,曲线和方程就不满足一一对应关系。2019-3-13探究3在直角坐标系中曲线C上的点与方程F(x,y)=0 的解一一对应的条件是什么?2019-3-13给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线上的点坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么这个方程f(x,y)=0叫做这条曲线C的方程
这条曲线C叫做这个方程的曲线定义分析特例归纳定义曲线的方程,方程的曲线2019-3-132、两者间的关系:点在曲线上即:曲线上所有点的集合与此曲线的方程的解集能够一一对应分析特例归纳定义2019-3-13例1判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错学习例题巩固定义2019-3-132019-3-132019-3-132019-3-13第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:证明已知曲线的方程的方法和步骤第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.2019-3-13做一做2019-3-132019-3-13在轨迹的基础上将轨迹和条件化为曲线和方程,当说某方程是曲线的方程或某曲线是方程的曲线时就意味着具备上述两个条件,只有具备上述两个方面的要求,才能将曲线的研究化为方程的研究,几何问题化为代数问题,以数助形正是解析几何的思想,本节课正是这一思想的基础。小结:2019-3-13习题2.1A组1题 优化设计2019-3-13
