13.6统计活动 同步练习(含解析)2023——2024学年沪教版(2020)高中数学必修第三册
文档属性
| 名称 | 13.6统计活动 同步练习(含解析)2023——2024学年沪教版(2020)高中数学必修第三册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 00:00:00 | ||
图片预览




文档简介
13.6 统计活动 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.地铁某换乘站设有编号为的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号
疏散乘客时间 120 220 160 140 200
用表示安全出口的疏散效率(疏散时间越短,疏散效率越高),给出下列四个说法:①;②;③;④.其中,正确说法的个数有( )
A.4个 B.3个 C.2个 D.1个
2.《黄帝内经》中十二时辰养生法认为:子时的睡眠对一天至关重要(子时是指23点到次日凌晨1点).相关数据表明,入睡时间越晚,沉睡时间越少,睡眠指数也就越低.根据某次的抽样数据,对早睡群体和晚睡群体的睡眠指数统计如图,则下列说法正确的是( )
A.在睡眠指数的人群中,早睡人数多于晚睡人数
B.早睡人群睡眠指数主要集中在
C.早睡人群睡眠指数的极差比晚睡人群睡眠指数的极差小
D.晚睡人群睡眠指数主要集中在
3.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果、可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为3.1; B.中位数为3,方差为1.6;
C.中位数为3,众数为2; D.平均数为3,中位数为2.
4.某中学组织三个年级的学生进行党史知识竞赛. 经统计,得到前名学生分布的扇形图(如图)和前名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前名的学生中,高一人数比高二人数多人
B.成绩前名的学生中,高一人数不超过人
C.成绩前名的学生中,高三人数不超过人
D.成绩第名到第名的学生中,高二人数比高一人数多
5.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图1所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力优于甲的逻辑推理能力
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
6.某企业有1000名职工,现按照总体的10%抽取样本,通过分层抽样得到如下年收入表:
年收入(元) 50万 15万 8万 4万 3万 1.2万
人数 1 6 15 55 20 3
某次工资上调中,只提高了最低收入,即从年收入1.2万元提高到2万元,其他职工的收入不变,则下列关于本企业职工年收入的说法中正确的是 ( )
A.平均数和众数都提高了 B.平均数和中位数都提高了
C.平均数不变,中位数提高了 D.中位数和众数不变,平均数提高了
7.某地区发生公共卫生事件期间,如果以“连续7天每天新增感染人数不超过5”作为未发生大规模感染的判断指标,那么根据连续7天的新增感染人数计算,下列各数据中,一定符合上述指标的是( )
①平均数.
②标准差.
③平均数且标准差.
④平均数且极差小于或等于2.
⑤众数等于1且极差小于或等于4.
A.①② B.③④ C.③④⑤ D.④⑤
8.某校为了解高二年级800名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场),随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 0 1 2 3 4 5 6 7
占调查人数的百分比 8% 10% 20% 26% 18% m% 4% 2%
则以下四个结论中正确的是( ).
①表中m的数值为12.
②估计该年级参加中华传统文化活动场数不高于2场的学生约为144人.
③若从该校高二年级800名学生中抽取容量为50的样本,则可以推测大约有31人至少参加了3场中华传统文化活动.
④从该校的高二年级的800名学生随机抽取80人,必有1人参加中华传统文化活动.
A.①② B.①③ C.①④ D.②③
二、多选题
9.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则以下四种说法中正确的是( )
A.甲的成绩的平均数等于乙的成绩的平均数
B.甲的成绩的中位数大于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差等于乙的成绩的极差
10.[多选]工业生产者出厂价格指数(PPI)是反映工业企业产品第一次出售时的出厂价格的变化趋势和变动幅度,是反映某一时期生产领域价格变动情况的重要经济指标,也是制定有关经济政策和国民经济核算的重要依据.根据下面提供的我国2020年1月—2021年11月的工业生产者出厂价格指数的月度同比(将上一年同月作为基期进行对比的价格指数)和月度环比(将上月作为基期进行对比的价格指数)涨跌情况的折线图判断,以下结论不正确的是( )
A.2020年各月的PPI在逐月增大
B.2020年各月的PPI均高于2019年同期水平
C.2021年1月—2021年11月各月的PPI在逐月减小
D.2021年1月—2021年11月各月的PPI均高于2020年同期水平
11.(多选)新式茶饮是指以上等茶叶通过萃取浓缩液,再根据消费者偏好,添加牛奶、坚果、柠檬等小料调制而成的饮料.如图为2022年我国消费者购买新式茶饮的频次扇形图及月均消费新式茶饮金额的条形图.
根据所给统计图,下列结论中正确的是( )
A.每周都消费新式茶饮的消费者占比不到90%
B.每天都消费新式茶饮的消费者占比超过20%
C.月均消费新式茶饮50~200元的消费者占比超过50%
D.月均消费新式茶饮超过100元的消费者占比超过60%
12.甲、乙二人在相同条件下各射击10次,每次中靶环数情况如图所示:
下列说法正确的是( )
A.从环数的平均数看,甲、乙二人射击水平相当
B.从环数的方差看,甲的成绩比乙稳定
C.从平均数和命中9环及9环以上的频数看,乙的成绩更好
D.从二人命中环数的走势看,甲更有潜力
三、填空题
13.甲、乙、丙、丁四人参加射击项目选拔赛,成绩如下, 则他们中参加奥运会的最佳人选是 .
甲 乙 丙 丁
平均环数 8.5 8.8 8.8 8
方 差 3.5 3.5 2.1 8.7
14.如图所示的茎叶图记录了甲,乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均数也相等,则x和y的值分别为 .
15.将参加英语口语测试的1000名学生编号为000,001,002,…,999,要从中抽取一个容量为50的样本.现按系统抽样的方法将1000名学生分为50组,如果第一组编号为000,001,002,…,019,且第一组随机抽取的编号为015,则抽取的第35个样本编号为 .
16.随着我国国民教育水平的提高,越来越多的有志青年报考研究生.现阶段,我国研究生入学考试科目为思政、外语和专业课三门,录取工作将这样进行:在每门课均及格(分)的考生中,按总分进行排序,择优录取.振华同学刚刚完成报考,尚有11周复习时间,下表是他每门课的复习时间和预计得分.设思政、外语和专业课分配到的周数分别为,则自然数数组 时,振华被录取的可能性最大.
科目 周数
0 1 2 3 4 5 6 7 8 9 10
思政 20 40 55 65 72 78 80 82 83 84 85
外语 30 45 53 58 62 65 68 70 72 74 75
专业课 50 70 85 90 93 95 96 96 96 96 96
四、解答题
17.某高中为配合爱国主义教育,开展国防科技知识竞赛,预赛后,将成绩最好的甲、乙两个班学生(每班都是40人)的得分情况做成如下的条形图(20道单项选择题,每题5分,满分100分).记甲、乙两班学生得分的平均数分别为,方差分别为,已求得
(1)分别求出甲、乙两班的学生得分为95分及以上的频率;
(2)试计算,并判断哪个班的学生的成绩波动更小.
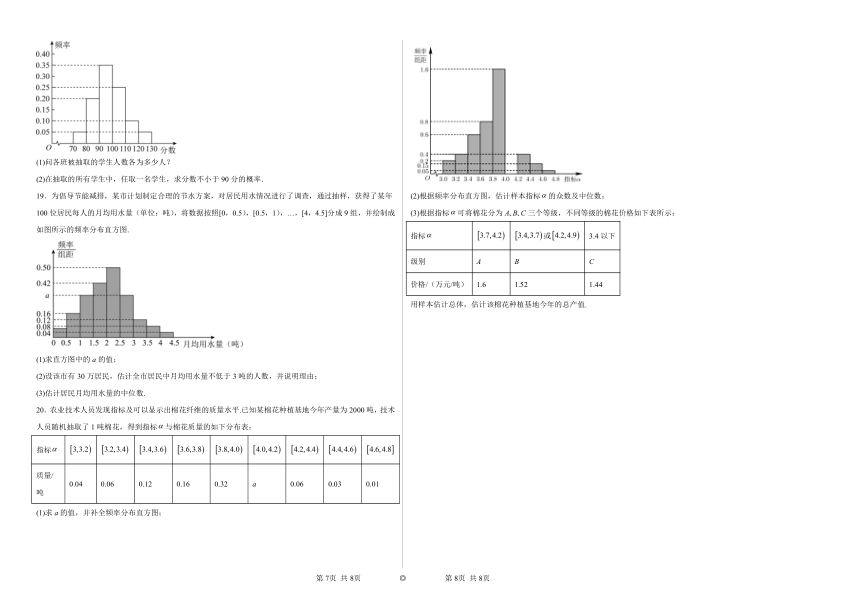
18.某校高三分为四个班.调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生数依次为22,,,人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
19.为倡导节能减排,某市计划制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,并绘制成如图所示的频率分布直方图.
(1)求直方图中的a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)估计居民月均用水量的中位数.
20.农业技术人员发现指标及可以显示出棉花纤维的质量水平.已知某棉花种植基地今年产量为2000吨,技术人员随机抽取了1吨棉花,得到指标与棉花质量的如下分布表:
指标
质量/吨 0.04 0.06 0.12 0.16 0.32 a 0.06 0.03 0.01
(1)求a的值,并补全频率分布直方图;
(2)根据频率分布直方图,估计样本指标的众数及中位数;
(3)根据指标可将棉花分为A B C三个等级,不同等级的棉花价格如下表所示:
指标 或 3.4以下
级别 A B C
价格/(万元/吨) 1.6 1.52 1.44
用样本估计总体,估计该棉花种植基地今年的总产值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据题意,列方程组,根据方程组解的值,判断正确的说法.
【详解】设每个出口每秒可疏散的人数为(),由题意,可得方程组:,可得:.
因为,所以,所以①正确;
因为,所以,所以②正确;
因为,所以,所以③正确;
因为,所以,所以④错误.
故选:B
2.B
【分析】根据统计图中的数据分析及极差的概念作出判断.
【详解】A选项,由于不知抽样数据中早睡和晚睡的人数,
从而无法确定在睡眠指数的人群中,早睡人数和晚睡人数,A错误;
B选项,由统计图可看出早睡人群睡眠指数主要集中在内,B正确;
C选项,在统计图中无法确定早睡人群睡眠指数和晚睡人群睡眠指数的极差,C错误.
D选项,晚睡人群睡眠指数主要集中在内,D错误.
故选:B
3.A
【分析】利用反证法即可证得选项A判断正确;利用举反例法即可证得选项BCD判断错误.
【详解】对于A,若平均数为2,出现点数6,可得方差,
故平均数为2,方差为3.1,一定没有出现点数6,故A正确.
对于B,当投掷骰子出现的结果为3,3,3,5,6时,
满足中位数为3,方差为:
,
此时出现点数为6,故B错误;
对于C,当投掷骰子出现结果为2,2,3,4,6时,
满足中位数为3,众数为2,可以出现点数6,故C错误;
对于D,当投掷骰子出现的结果为1,1,2,5,6时,
满足平均数为3,中位数为2,可以出现点数6,故D错误.
故选:A
4.D
【分析】根据饼状图和条形图提供的数据判断.
【详解】由饼状图,成绩前200名的200人中,高一人数比高二人数多,A正确;
由条形图知高一学生在前200名中,前100和后100人数相等,因此高一人数为,B正确;
成绩前50名的50人中,高一人数为,因此高三最多有32人,C正确;
第51到100名的50人中,高一人数为,故高二最多有23人,因此高二人数比高一少,D错误.
故选:D.
5.C
【分析】利用雷达图对每一个选项的命题逐一分析推理得解.
【详解】A:甲的逻辑推理能力指标值为4,优于乙的逻辑推理能力指标值为3,故错误;
B:甲的数学建模能力指标值为3,乙的直观想象能力指标值为5,所以乙的直观想象能力指标值优于甲的数学建模能力指标值,故错误;
C:甲的六维能力指标值的平均值为,乙的六维能力指标值的平均值为,因为,故正确;
D:甲的数学运算能力指标值为4,甲的直观想象能力指标值为5,所以甲的数学运算能力指标值不优于甲的直观想象能力指标值,故错误.
故选:C
6.D
【分析】首先说明平均数提高了,再说明中位数和众数没有改变.
【详解】解:由于提高了最低收入,即从年收入1.2万元提高到2万元,其他职工的收入不变,所以平均数提高了.
提高最低收入后,有1人年收入50万,6个人年收入15万,15个人年收入8万,55个人年收入4万,20个人年收入3万,3个人年收入2万,所以众数还是4万,中位数还是4万,众数和中位数没有变化.
故选:D
7.D
【分析】假设连续7天新增感染人数为1 2 3 3 3 3 6,得到①②③错误;若极差等于0或者1,在平均数的条件下符合指标,得出④正确,众数等于1且极差小于或等于4,符合指标,⑤正确.
【详解】提示:由题意,假设连续7天新增感染人数为1 2 3 3 3 3 6,易知满足平均数且标准差,但是不符合指标,所以①②③错误.
若极差等于0或者1,在平均数的条件下符合指标;
若极差等于2,则极小值与极大值的组合可能有:0和2;1和3;2和4;3和5;4和6.
在平均数的条件下,只有前3种可能符合指标,所以④正确.
若众数为1,且极差最大为4,则最小值为0或者1,最大数不超过5,所以⑤正确.
故选:D.
8.B
【分析】根据频率之和等于1可判断①;通过样本估计总体计算可判断②③;由随机事件含义可判断④.
【详解】由,得,①正确;
,②错误;
至少参加了3场中华传统文化活动的百分比为
所以,③正确;
抽样是一种可能性问题,虽然参加活动的可能性较大,但不一定发生,故④错误.
故选:B
9.ABCD
【分析】利用条形图结合平均数、中位数、方差、极差的相关概念一一判定选项即可.
【详解】由条形图可知甲、乙的平均数分别为:,故A正确;
甲、乙的中位数分别为,故B正确;
甲、乙的方差分别为,
,故C正确;
甲、乙的极差分别为,故D正确.
故选:ABCD
10.ABC
【分析】
由折线图直接观察可一一判定选项.
【详解】对于A,2020年前5个月的PPI月度环比增长均为负值,即在逐月减小,故A错误;
对于B,2020年2月之后各月的PPI月度同比增长均为负值,即低于2019年同期水平,故B错误;
对于C,2021年1月—2021年11月各月的PPI月度环比增长均不为负,即逐月增大,故C错误;
对于D,2021年1月—2021年11月各月的PPI月度同比增长均为正值,即高于2020年同期水平,故D正确.
故选:ABC.
11.BC
【分析】根据统计图一一分析选项即可.
【详解】每周都消费新式茶饮的消费者占比,A错误;
每天都消费新式茶饮的消费者占比,B正确;
月均消费新式茶饮50~200元的消费者占比,C正确;
月均消费新式茶饮超过100元的消费者占比,D错误.
故选:BC
12.ABC
【分析】求出甲乙的平均数和方差,即可得出结论.
【详解】由题意及图得,
甲射击 10 次中靶环数分别为.
将它们由小到大排列为.
乙射击 10 次中靶环数分别为.
将它们由小到大排列为.
甲平均值:(环),
乙平均值:(环),
甲方差:,
乙方差:
,
A项,甲平均值等于乙平均值,故A正确;
B项,,甲的成绩比乙稳定,B正确;
C项,甲乙平均数均为7,甲命中9环及9环以上的频数为1,乙命中9环及9环以上的频数为3,故乙的成绩更好,C正确;
D项,从二人命中环数的走势看,甲成绩逐渐平稳,乙成绩仍有上升趋势,故乙更有潜力,D错误.
故选:ABC
13.丙
【分析】根据数据方差越小越稳定即可解决.
【详解】由平均数及方差的定义知,丙的平均成绩较高且较稳定.
故答案为:丙
14.3和5
【分析】根据中位数和平均数的知识求得正确答案.
【详解】依题意,这两组数据的中位数相等,且平均数也相等,
所以且,
解得.
故答案为:3和5
15.695
【分析】根据系统抽样的知识求得正确答案.
【详解】依题意,抽取的第35个样本编号为.
故答案为:
16.
【分析】根据题意,分别保证各科及格,再由得分效益最大求解.
【详解】首先保证各学科均及格,则思政、外语、专业课分别需要3周,4周,2周,还有剩余复习时间3周,剩余时间复习一周思政可提高7分,复习外语可提高3分,复习专业课可提高15分,故先安排一周复习专业课,剩余2周,若再复习专业课一周可提高5分,从得分效益来看,先安排一周复习思政,剩一周再复习思政可提高6分,故安排复习思政,
综上,安排5周思政复习,4周外语复习,2周专业课复习,总分最高,
故答案为:
17.(1)0.3,0.425;
(2),甲班学生的成绩波动更小.
【分析】(1)利用条形图计算频率即可;
(2)利用方差公式计算结合及方差的意义判定即可.
【详解】(1)甲班得分为95分及以上的学生有人,故频率为;
乙班得分为95分及以上的学生有人,故频率为
(2)因为,
所以方差
;
显然,所以,甲班学生的成绩波动更小.
18.(1)22人,24人,26人,28人
(2)0.75
【分析】(1)由频率分布条形图知抽取的学生总数,各班被抽取的学生人数成等差数列,设公差为d,则求出可得答案;
(2)任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率,结合频率分布直方图可得答案.
【详解】(1)由频率等于频数除以总数知,抽取的学生总数为人,又各班被抽取的学生人数成等差数列,人数最少的班被抽取了22人,则首项为22.设公差为d,则,,因此各班被抽取的人数分别是22人,24人,26人,28人;
(2)在抽取的所有学生中,任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率,而分数低于90分的概率等于,因此所求概率为10.25=0.75.
19.(1)0.30
(2)36000,理由见解析
(3)2.04
【分析】(1)根据频率之和为求得.
(2)通过全市居民中月均用水量不低于3吨的频率求得人数.
(3)根据中位数的求法求得中位数.
【详解】(1)由频率分布直方图可知,月用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1)知,100位居民月均水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300000×0.12=36000.
(3)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以.
由0.50×(x-2)=0.5-0.48,解得x=2.04,可估计居民月均用水量的中位数为2.04吨.
20.(1),频率分布直方图答案见解析;
(2)众数为,中位数为3.875;
(3)(万元).
【分析】(1)由频率分布直方图和统计表可计算求得,由此可补全频率分布直方图;
(2)由频率分布直方图估计众数和中位数的方法直接求解即可;
(3)计算求得1吨样本的产值,进而可得今年的总产值.
【详解】(1)由分布表知,,解得.
在频率分布直方图中对应的为,补全频率分布直方图如下:
(2)由频率分布直方图知,指标落在区间上的频率最大,
故众数为.
因为,且,
所以中位数在区间上,
设中位数为x,则,
解得,即中位数为3.875.
(3)由题可得1吨样本的产值为(万元),
估算棉花种植基地今年的总产值为:(万元).
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.地铁某换乘站设有编号为的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号
疏散乘客时间 120 220 160 140 200
用表示安全出口的疏散效率(疏散时间越短,疏散效率越高),给出下列四个说法:①;②;③;④.其中,正确说法的个数有( )
A.4个 B.3个 C.2个 D.1个
2.《黄帝内经》中十二时辰养生法认为:子时的睡眠对一天至关重要(子时是指23点到次日凌晨1点).相关数据表明,入睡时间越晚,沉睡时间越少,睡眠指数也就越低.根据某次的抽样数据,对早睡群体和晚睡群体的睡眠指数统计如图,则下列说法正确的是( )
A.在睡眠指数的人群中,早睡人数多于晚睡人数
B.早睡人群睡眠指数主要集中在
C.早睡人群睡眠指数的极差比晚睡人群睡眠指数的极差小
D.晚睡人群睡眠指数主要集中在
3.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果、可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为3.1; B.中位数为3,方差为1.6;
C.中位数为3,众数为2; D.平均数为3,中位数为2.
4.某中学组织三个年级的学生进行党史知识竞赛. 经统计,得到前名学生分布的扇形图(如图)和前名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前名的学生中,高一人数比高二人数多人
B.成绩前名的学生中,高一人数不超过人
C.成绩前名的学生中,高三人数不超过人
D.成绩第名到第名的学生中,高二人数比高一人数多
5.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图1所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力优于甲的逻辑推理能力
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
6.某企业有1000名职工,现按照总体的10%抽取样本,通过分层抽样得到如下年收入表:
年收入(元) 50万 15万 8万 4万 3万 1.2万
人数 1 6 15 55 20 3
某次工资上调中,只提高了最低收入,即从年收入1.2万元提高到2万元,其他职工的收入不变,则下列关于本企业职工年收入的说法中正确的是 ( )
A.平均数和众数都提高了 B.平均数和中位数都提高了
C.平均数不变,中位数提高了 D.中位数和众数不变,平均数提高了
7.某地区发生公共卫生事件期间,如果以“连续7天每天新增感染人数不超过5”作为未发生大规模感染的判断指标,那么根据连续7天的新增感染人数计算,下列各数据中,一定符合上述指标的是( )
①平均数.
②标准差.
③平均数且标准差.
④平均数且极差小于或等于2.
⑤众数等于1且极差小于或等于4.
A.①② B.③④ C.③④⑤ D.④⑤
8.某校为了解高二年级800名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场),随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 0 1 2 3 4 5 6 7
占调查人数的百分比 8% 10% 20% 26% 18% m% 4% 2%
则以下四个结论中正确的是( ).
①表中m的数值为12.
②估计该年级参加中华传统文化活动场数不高于2场的学生约为144人.
③若从该校高二年级800名学生中抽取容量为50的样本,则可以推测大约有31人至少参加了3场中华传统文化活动.
④从该校的高二年级的800名学生随机抽取80人,必有1人参加中华传统文化活动.
A.①② B.①③ C.①④ D.②③
二、多选题
9.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则以下四种说法中正确的是( )
A.甲的成绩的平均数等于乙的成绩的平均数
B.甲的成绩的中位数大于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差等于乙的成绩的极差
10.[多选]工业生产者出厂价格指数(PPI)是反映工业企业产品第一次出售时的出厂价格的变化趋势和变动幅度,是反映某一时期生产领域价格变动情况的重要经济指标,也是制定有关经济政策和国民经济核算的重要依据.根据下面提供的我国2020年1月—2021年11月的工业生产者出厂价格指数的月度同比(将上一年同月作为基期进行对比的价格指数)和月度环比(将上月作为基期进行对比的价格指数)涨跌情况的折线图判断,以下结论不正确的是( )
A.2020年各月的PPI在逐月增大
B.2020年各月的PPI均高于2019年同期水平
C.2021年1月—2021年11月各月的PPI在逐月减小
D.2021年1月—2021年11月各月的PPI均高于2020年同期水平
11.(多选)新式茶饮是指以上等茶叶通过萃取浓缩液,再根据消费者偏好,添加牛奶、坚果、柠檬等小料调制而成的饮料.如图为2022年我国消费者购买新式茶饮的频次扇形图及月均消费新式茶饮金额的条形图.
根据所给统计图,下列结论中正确的是( )
A.每周都消费新式茶饮的消费者占比不到90%
B.每天都消费新式茶饮的消费者占比超过20%
C.月均消费新式茶饮50~200元的消费者占比超过50%
D.月均消费新式茶饮超过100元的消费者占比超过60%
12.甲、乙二人在相同条件下各射击10次,每次中靶环数情况如图所示:
下列说法正确的是( )
A.从环数的平均数看,甲、乙二人射击水平相当
B.从环数的方差看,甲的成绩比乙稳定
C.从平均数和命中9环及9环以上的频数看,乙的成绩更好
D.从二人命中环数的走势看,甲更有潜力
三、填空题
13.甲、乙、丙、丁四人参加射击项目选拔赛,成绩如下, 则他们中参加奥运会的最佳人选是 .
甲 乙 丙 丁
平均环数 8.5 8.8 8.8 8
方 差 3.5 3.5 2.1 8.7
14.如图所示的茎叶图记录了甲,乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均数也相等,则x和y的值分别为 .
15.将参加英语口语测试的1000名学生编号为000,001,002,…,999,要从中抽取一个容量为50的样本.现按系统抽样的方法将1000名学生分为50组,如果第一组编号为000,001,002,…,019,且第一组随机抽取的编号为015,则抽取的第35个样本编号为 .
16.随着我国国民教育水平的提高,越来越多的有志青年报考研究生.现阶段,我国研究生入学考试科目为思政、外语和专业课三门,录取工作将这样进行:在每门课均及格(分)的考生中,按总分进行排序,择优录取.振华同学刚刚完成报考,尚有11周复习时间,下表是他每门课的复习时间和预计得分.设思政、外语和专业课分配到的周数分别为,则自然数数组 时,振华被录取的可能性最大.
科目 周数
0 1 2 3 4 5 6 7 8 9 10
思政 20 40 55 65 72 78 80 82 83 84 85
外语 30 45 53 58 62 65 68 70 72 74 75
专业课 50 70 85 90 93 95 96 96 96 96 96
四、解答题
17.某高中为配合爱国主义教育,开展国防科技知识竞赛,预赛后,将成绩最好的甲、乙两个班学生(每班都是40人)的得分情况做成如下的条形图(20道单项选择题,每题5分,满分100分).记甲、乙两班学生得分的平均数分别为,方差分别为,已求得
(1)分别求出甲、乙两班的学生得分为95分及以上的频率;
(2)试计算,并判断哪个班的学生的成绩波动更小.
18.某校高三分为四个班.调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生数依次为22,,,人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
19.为倡导节能减排,某市计划制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,并绘制成如图所示的频率分布直方图.
(1)求直方图中的a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)估计居民月均用水量的中位数.
20.农业技术人员发现指标及可以显示出棉花纤维的质量水平.已知某棉花种植基地今年产量为2000吨,技术人员随机抽取了1吨棉花,得到指标与棉花质量的如下分布表:
指标
质量/吨 0.04 0.06 0.12 0.16 0.32 a 0.06 0.03 0.01
(1)求a的值,并补全频率分布直方图;
(2)根据频率分布直方图,估计样本指标的众数及中位数;
(3)根据指标可将棉花分为A B C三个等级,不同等级的棉花价格如下表所示:
指标 或 3.4以下
级别 A B C
价格/(万元/吨) 1.6 1.52 1.44
用样本估计总体,估计该棉花种植基地今年的总产值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据题意,列方程组,根据方程组解的值,判断正确的说法.
【详解】设每个出口每秒可疏散的人数为(),由题意,可得方程组:,可得:.
因为,所以,所以①正确;
因为,所以,所以②正确;
因为,所以,所以③正确;
因为,所以,所以④错误.
故选:B
2.B
【分析】根据统计图中的数据分析及极差的概念作出判断.
【详解】A选项,由于不知抽样数据中早睡和晚睡的人数,
从而无法确定在睡眠指数的人群中,早睡人数和晚睡人数,A错误;
B选项,由统计图可看出早睡人群睡眠指数主要集中在内,B正确;
C选项,在统计图中无法确定早睡人群睡眠指数和晚睡人群睡眠指数的极差,C错误.
D选项,晚睡人群睡眠指数主要集中在内,D错误.
故选:B
3.A
【分析】利用反证法即可证得选项A判断正确;利用举反例法即可证得选项BCD判断错误.
【详解】对于A,若平均数为2,出现点数6,可得方差,
故平均数为2,方差为3.1,一定没有出现点数6,故A正确.
对于B,当投掷骰子出现的结果为3,3,3,5,6时,
满足中位数为3,方差为:
,
此时出现点数为6,故B错误;
对于C,当投掷骰子出现结果为2,2,3,4,6时,
满足中位数为3,众数为2,可以出现点数6,故C错误;
对于D,当投掷骰子出现的结果为1,1,2,5,6时,
满足平均数为3,中位数为2,可以出现点数6,故D错误.
故选:A
4.D
【分析】根据饼状图和条形图提供的数据判断.
【详解】由饼状图,成绩前200名的200人中,高一人数比高二人数多,A正确;
由条形图知高一学生在前200名中,前100和后100人数相等,因此高一人数为,B正确;
成绩前50名的50人中,高一人数为,因此高三最多有32人,C正确;
第51到100名的50人中,高一人数为,故高二最多有23人,因此高二人数比高一少,D错误.
故选:D.
5.C
【分析】利用雷达图对每一个选项的命题逐一分析推理得解.
【详解】A:甲的逻辑推理能力指标值为4,优于乙的逻辑推理能力指标值为3,故错误;
B:甲的数学建模能力指标值为3,乙的直观想象能力指标值为5,所以乙的直观想象能力指标值优于甲的数学建模能力指标值,故错误;
C:甲的六维能力指标值的平均值为,乙的六维能力指标值的平均值为,因为,故正确;
D:甲的数学运算能力指标值为4,甲的直观想象能力指标值为5,所以甲的数学运算能力指标值不优于甲的直观想象能力指标值,故错误.
故选:C
6.D
【分析】首先说明平均数提高了,再说明中位数和众数没有改变.
【详解】解:由于提高了最低收入,即从年收入1.2万元提高到2万元,其他职工的收入不变,所以平均数提高了.
提高最低收入后,有1人年收入50万,6个人年收入15万,15个人年收入8万,55个人年收入4万,20个人年收入3万,3个人年收入2万,所以众数还是4万,中位数还是4万,众数和中位数没有变化.
故选:D
7.D
【分析】假设连续7天新增感染人数为1 2 3 3 3 3 6,得到①②③错误;若极差等于0或者1,在平均数的条件下符合指标,得出④正确,众数等于1且极差小于或等于4,符合指标,⑤正确.
【详解】提示:由题意,假设连续7天新增感染人数为1 2 3 3 3 3 6,易知满足平均数且标准差,但是不符合指标,所以①②③错误.
若极差等于0或者1,在平均数的条件下符合指标;
若极差等于2,则极小值与极大值的组合可能有:0和2;1和3;2和4;3和5;4和6.
在平均数的条件下,只有前3种可能符合指标,所以④正确.
若众数为1,且极差最大为4,则最小值为0或者1,最大数不超过5,所以⑤正确.
故选:D.
8.B
【分析】根据频率之和等于1可判断①;通过样本估计总体计算可判断②③;由随机事件含义可判断④.
【详解】由,得,①正确;
,②错误;
至少参加了3场中华传统文化活动的百分比为
所以,③正确;
抽样是一种可能性问题,虽然参加活动的可能性较大,但不一定发生,故④错误.
故选:B
9.ABCD
【分析】利用条形图结合平均数、中位数、方差、极差的相关概念一一判定选项即可.
【详解】由条形图可知甲、乙的平均数分别为:,故A正确;
甲、乙的中位数分别为,故B正确;
甲、乙的方差分别为,
,故C正确;
甲、乙的极差分别为,故D正确.
故选:ABCD
10.ABC
【分析】
由折线图直接观察可一一判定选项.
【详解】对于A,2020年前5个月的PPI月度环比增长均为负值,即在逐月减小,故A错误;
对于B,2020年2月之后各月的PPI月度同比增长均为负值,即低于2019年同期水平,故B错误;
对于C,2021年1月—2021年11月各月的PPI月度环比增长均不为负,即逐月增大,故C错误;
对于D,2021年1月—2021年11月各月的PPI月度同比增长均为正值,即高于2020年同期水平,故D正确.
故选:ABC.
11.BC
【分析】根据统计图一一分析选项即可.
【详解】每周都消费新式茶饮的消费者占比,A错误;
每天都消费新式茶饮的消费者占比,B正确;
月均消费新式茶饮50~200元的消费者占比,C正确;
月均消费新式茶饮超过100元的消费者占比,D错误.
故选:BC
12.ABC
【分析】求出甲乙的平均数和方差,即可得出结论.
【详解】由题意及图得,
甲射击 10 次中靶环数分别为.
将它们由小到大排列为.
乙射击 10 次中靶环数分别为.
将它们由小到大排列为.
甲平均值:(环),
乙平均值:(环),
甲方差:,
乙方差:
,
A项,甲平均值等于乙平均值,故A正确;
B项,,甲的成绩比乙稳定,B正确;
C项,甲乙平均数均为7,甲命中9环及9环以上的频数为1,乙命中9环及9环以上的频数为3,故乙的成绩更好,C正确;
D项,从二人命中环数的走势看,甲成绩逐渐平稳,乙成绩仍有上升趋势,故乙更有潜力,D错误.
故选:ABC
13.丙
【分析】根据数据方差越小越稳定即可解决.
【详解】由平均数及方差的定义知,丙的平均成绩较高且较稳定.
故答案为:丙
14.3和5
【分析】根据中位数和平均数的知识求得正确答案.
【详解】依题意,这两组数据的中位数相等,且平均数也相等,
所以且,
解得.
故答案为:3和5
15.695
【分析】根据系统抽样的知识求得正确答案.
【详解】依题意,抽取的第35个样本编号为.
故答案为:
16.
【分析】根据题意,分别保证各科及格,再由得分效益最大求解.
【详解】首先保证各学科均及格,则思政、外语、专业课分别需要3周,4周,2周,还有剩余复习时间3周,剩余时间复习一周思政可提高7分,复习外语可提高3分,复习专业课可提高15分,故先安排一周复习专业课,剩余2周,若再复习专业课一周可提高5分,从得分效益来看,先安排一周复习思政,剩一周再复习思政可提高6分,故安排复习思政,
综上,安排5周思政复习,4周外语复习,2周专业课复习,总分最高,
故答案为:
17.(1)0.3,0.425;
(2),甲班学生的成绩波动更小.
【分析】(1)利用条形图计算频率即可;
(2)利用方差公式计算结合及方差的意义判定即可.
【详解】(1)甲班得分为95分及以上的学生有人,故频率为;
乙班得分为95分及以上的学生有人,故频率为
(2)因为,
所以方差
;
显然,所以,甲班学生的成绩波动更小.
18.(1)22人,24人,26人,28人
(2)0.75
【分析】(1)由频率分布条形图知抽取的学生总数,各班被抽取的学生人数成等差数列,设公差为d,则求出可得答案;
(2)任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率,结合频率分布直方图可得答案.
【详解】(1)由频率等于频数除以总数知,抽取的学生总数为人,又各班被抽取的学生人数成等差数列,人数最少的班被抽取了22人,则首项为22.设公差为d,则,,因此各班被抽取的人数分别是22人,24人,26人,28人;
(2)在抽取的所有学生中,任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率,而分数低于90分的概率等于,因此所求概率为10.25=0.75.
19.(1)0.30
(2)36000,理由见解析
(3)2.04
【分析】(1)根据频率之和为求得.
(2)通过全市居民中月均用水量不低于3吨的频率求得人数.
(3)根据中位数的求法求得中位数.
【详解】(1)由频率分布直方图可知,月用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1)知,100位居民月均水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300000×0.12=36000.
(3)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以.
由0.50×(x-2)=0.5-0.48,解得x=2.04,可估计居民月均用水量的中位数为2.04吨.
20.(1),频率分布直方图答案见解析;
(2)众数为,中位数为3.875;
(3)(万元).
【分析】(1)由频率分布直方图和统计表可计算求得,由此可补全频率分布直方图;
(2)由频率分布直方图估计众数和中位数的方法直接求解即可;
(3)计算求得1吨样本的产值,进而可得今年的总产值.
【详解】(1)由分布表知,,解得.
在频率分布直方图中对应的为,补全频率分布直方图如下:
(2)由频率分布直方图知,指标落在区间上的频率最大,
故众数为.
因为,且,
所以中位数在区间上,
设中位数为x,则,
解得,即中位数为3.875.
(3)由题可得1吨样本的产值为(万元),
估算棉花种植基地今年的总产值为:(万元).
答案第1页,共2页
答案第1页,共2页
同课章节目录
