数学人教A版(2019)选择性必修第三册6.2.1排列 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.2.1排列 课件(共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 23:36:22 | ||
图片预览







文档简介
(共27张PPT)
人教A版 选择性必修 第二册
6.2.1 排列
第六章 计数原理
人教A版 数学 选择性必修 第二册
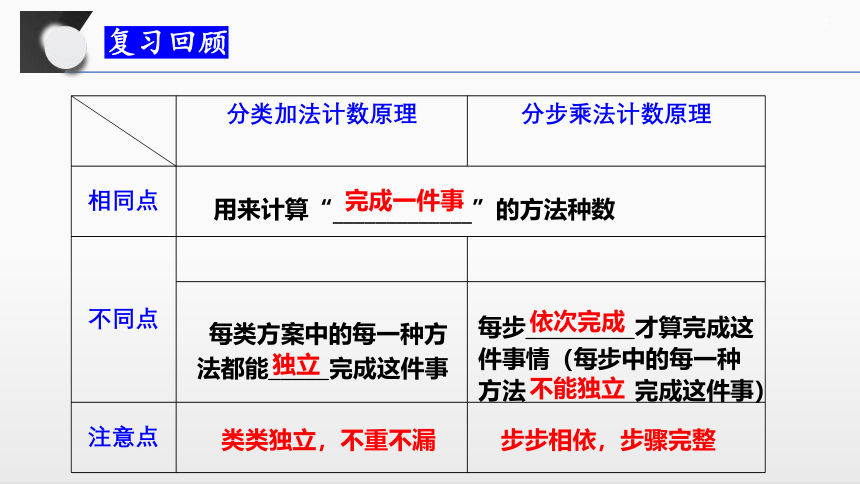
分类加法计数原理分步乘法计数原理相同点不同点注意点完成一件事每类方案中的每一种方法都能_____完成这件事每步_________才算完成这件事情(每步中的每一种方法完成这件事)类类独立,不重不漏步步相依,步骤完整独立依次完成复习回顾不能独立用来计算“_____________”的方法种数创设情境
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
新知探究
问题提出
“从____名同学选出____名,
___名参加____的活动,另__名参加___的活动”
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
分步
第1步,确定参加_____活动的同学;
甲
乙
丙
根据________________原理,
上午
下午
每种情况均有__种选法
乙
丙
甲
丙
甲
乙
第2步,确定参加_____活动的同学.
___种选法
相应的选法
不同的选法种数为:____________
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
新知探究
问题提出
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
甲
乙
丙
上午
下午
每种情况均有2种选法
乙
丙
甲
丙
甲
乙
3种选法
相应的选法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
新知探究
问题提出
甲乙、乙甲是相同的选法吗?
问题1中的顺序是什么?
问题1的顺序为参加活动的顺序,
即参加上午的活动在前,
参加下午的活动在后.
不是
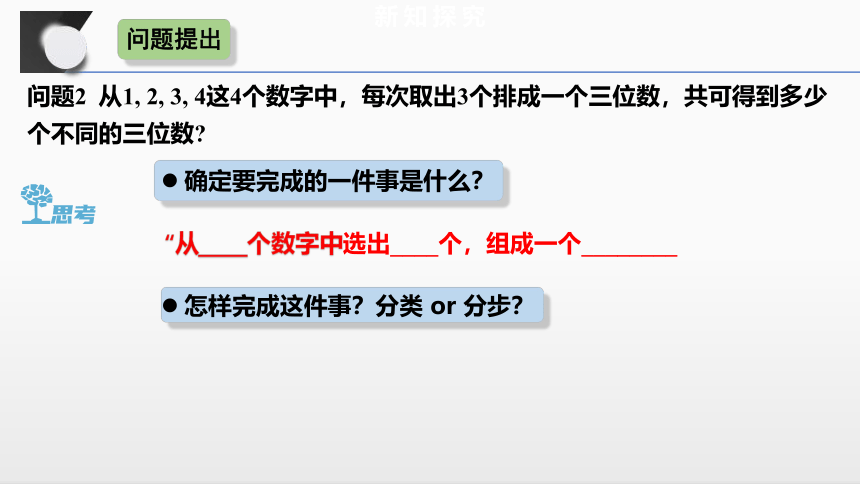
如果把问题1中对象“同学”抽象为“元素”.那么还可以怎样叙述问题1 问题1从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?从______________中任取____个,然后按_______________,共有多少种_________的______方法 ?问题提出问题2从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数 同学们模仿问题1的解答过程完成问题2的解答.问题提出新知探究
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
“从____个数字中选出____个,组成一个________
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题提出
根据_________________原理,
第1步,确定百位上的数字
第2步,确定十位上的数字
第3步,确定个位上的数字
百位
1
2
3
4
十位
共有4种方法
每类有3种方法
每类有2种方法
不同的排法种数为:____________.
个位
2 3 4
1 3 4
1 2 4
1 2 3
3 4
2 4
1 3
3 4
1 4
1 3
2 4
1 4
1 2
2 3
1 3
1 2
分步
新知探究
树状图
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题提出
问题2从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的 三位数 百位在前,十位居中,个位在后.123、132是相同的选法吗?问题2中的顺序是什么?百位1十位个位2 3 43 42 41 3不是问题提出
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
从______________中任取____个,然后按_______________,共有多少种_________的______方法 ?
如果把问题2中对象“数字”抽象为“元素”.那么还可以怎样叙述问题2
问题提出
问题1 . 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同
的排法
问题2 .从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
思考?上述两个问题的共同特点是?能否推广到一般情形?
概念形成
抽象概括
思考:以上问题1、2的共同特点是什么?你能将它们推广到一般情形吗?
元素
问题1
选出的“同学”
问题2
取出的“数字”
按上午、下午安排选出的2名同学
按百位、十位、个位把取出的3个数字
排成一个三位数
把取出的元素按一定顺序排成一列
从一些__________中取出_________,并按照____________排成一列的方法数
我们把这种计数方法称为排列.
概念形成
不同元素
部分元素
一定的顺序
追问(1):n个元素能相同吗?
追问(3):m个元素能相同吗?
追问(2):可否重复选取元素?
排列定义
定义
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
不能
不能重复
不能
研究排列问题时,都是从一些不同元素中任取部分不同元素,
既_____________,又没有______________________________
没有重复元素
重复抽取同一元素的情况
定义
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
排列定义
两个排列相同
①元素完全相同
②元素的排列顺序也相同
定义包含两个基本内容:
①取出一部分元素
②按一定顺序排列
有无顺序是判断一个问题是不是排列问题的重要标志
例1: 下列问题中哪些是排列问题?
(1)从50名学生中抽2名学生开会
(2)从50名学生中选2名做正、副组长
(3)从1,2,3,5中任取两个数相乘
(4)从1,2,3,5,中任取两个数相除
(5)某条火车路线有10个车站,共需要多少种车票?
(6)某条火车路线有10个车站,共需要多少种票价?
是
是
是
否
否
否
题型1 排列的概念
规律方法
排列问题的判断方法
元素的无重复性
元素被安排的有序性
检验它是否有序的依据就是____________________,看结果是否变化,
有变化就是有顺序,无变化就是无顺序.
变换元素的位置
例2某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛 题型2排列的简单应用要完成的“一件事”是什么?abcdef每2队之间需比赛2场a→主队,b→客队a→客队,b→主队要完成的“一件事”是否与“顺序”有关?主队、客队是否为排列问题?是排列从_____支队中选出_____支,____支作为______, ____支作为______例2某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛 如何用计数原理求出比赛场数?题型2排列的简单应用练习2:学校乒乓团体比赛采用5场3胜制(5场单打),每支球队派3名运动员参赛,前3场比赛每名运动员各出场1次,其中第1,2位出场的运动员在后2场比赛中还将各出场1次.(1)从5名运动员中选3名参加比赛,前3场比赛有几种出场情况 (2)甲、乙、丙3名运动员参加比赛,写出所有可能的出场情况.题型2排列的简单应用例3(1) 一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法 (2) 学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少 种不同的选法 追问(3):例3(1)是排列问题吗?追问(4):例3(2)是排列问题吗?不满足元素的互异性追问(1):这两个问题的不同点是什么?题型2排列的简单应用追问(2):是否有重复抽取同一元素的情况?是排列不是排列例3(1) 一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法 (2) 学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少 种不同的选法 题型2排列的简单应用追问(5):如何用计数原理求解?练习(1)有7本不同的书,从中选3本送给3名同学,每人各1本,共有多少种不同的取法 (2)有7种不同的书,要买3本送给3名同学,每人各1本,共有多少种不同的取法 题型2排列的简单应用
反思感悟
解决此类相似问题时,首先要分清楚是不是排列问题,其次使用分步乘法计数原理求排列总数时,要做到步骤完整,步与步之间相互独立,然后把完成每一步的方法数相乘即可得到总数. .
课堂小结
课堂小结一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).1.排列的定义:注意排列的两个关键要素:元素互异,元素按顺序排列.2.排列的简单计算:树状图分析、列举、分步乘法计数原理.
人教A版 选择性必修 第二册
6.2.1 排列
第六章 计数原理
人教A版 数学 选择性必修 第二册
分类加法计数原理分步乘法计数原理相同点不同点注意点完成一件事每类方案中的每一种方法都能_____完成这件事每步_________才算完成这件事情(每步中的每一种方法完成这件事)类类独立,不重不漏步步相依,步骤完整独立依次完成复习回顾不能独立用来计算“_____________”的方法种数创设情境
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
新知探究
问题提出
“从____名同学选出____名,
___名参加____的活动,另__名参加___的活动”
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
分步
第1步,确定参加_____活动的同学;
甲
乙
丙
根据________________原理,
上午
下午
每种情况均有__种选法
乙
丙
甲
丙
甲
乙
第2步,确定参加_____活动的同学.
___种选法
相应的选法
不同的选法种数为:____________
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
新知探究
问题提出
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
甲
乙
丙
上午
下午
每种情况均有2种选法
乙
丙
甲
丙
甲
乙
3种选法
相应的选法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
新知探究
问题提出
甲乙、乙甲是相同的选法吗?
问题1中的顺序是什么?
问题1的顺序为参加活动的顺序,
即参加上午的活动在前,
参加下午的活动在后.
不是
如果把问题1中对象“同学”抽象为“元素”.那么还可以怎样叙述问题1 问题1从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?从______________中任取____个,然后按_______________,共有多少种_________的______方法 ?问题提出问题2从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数 同学们模仿问题1的解答过程完成问题2的解答.问题提出新知探究
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
“从____个数字中选出____个,组成一个________
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题提出
根据_________________原理,
第1步,确定百位上的数字
第2步,确定十位上的数字
第3步,确定个位上的数字
百位
1
2
3
4
十位
共有4种方法
每类有3种方法
每类有2种方法
不同的排法种数为:____________.
个位
2 3 4
1 3 4
1 2 4
1 2 3
3 4
2 4
1 3
3 4
1 4
1 3
2 4
1 4
1 2
2 3
1 3
1 2
分步
新知探究
树状图
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题提出
问题2从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的 三位数 百位在前,十位居中,个位在后.123、132是相同的选法吗?问题2中的顺序是什么?百位1十位个位2 3 43 42 41 3不是问题提出
问题2 从1, 2, 3, 4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
从______________中任取____个,然后按_______________,共有多少种_________的______方法 ?
如果把问题2中对象“数字”抽象为“元素”.那么还可以怎样叙述问题2
问题提出
问题1 . 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同
的排法
问题2 .从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
思考?上述两个问题的共同特点是?能否推广到一般情形?
概念形成
抽象概括
思考:以上问题1、2的共同特点是什么?你能将它们推广到一般情形吗?
元素
问题1
选出的“同学”
问题2
取出的“数字”
按上午、下午安排选出的2名同学
按百位、十位、个位把取出的3个数字
排成一个三位数
把取出的元素按一定顺序排成一列
从一些__________中取出_________,并按照____________排成一列的方法数
我们把这种计数方法称为排列.
概念形成
不同元素
部分元素
一定的顺序
追问(1):n个元素能相同吗?
追问(3):m个元素能相同吗?
追问(2):可否重复选取元素?
排列定义
定义
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
不能
不能重复
不能
研究排列问题时,都是从一些不同元素中任取部分不同元素,
既_____________,又没有______________________________
没有重复元素
重复抽取同一元素的情况
定义
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
排列定义
两个排列相同
①元素完全相同
②元素的排列顺序也相同
定义包含两个基本内容:
①取出一部分元素
②按一定顺序排列
有无顺序是判断一个问题是不是排列问题的重要标志
例1: 下列问题中哪些是排列问题?
(1)从50名学生中抽2名学生开会
(2)从50名学生中选2名做正、副组长
(3)从1,2,3,5中任取两个数相乘
(4)从1,2,3,5,中任取两个数相除
(5)某条火车路线有10个车站,共需要多少种车票?
(6)某条火车路线有10个车站,共需要多少种票价?
是
是
是
否
否
否
题型1 排列的概念
规律方法
排列问题的判断方法
元素的无重复性
元素被安排的有序性
检验它是否有序的依据就是____________________,看结果是否变化,
有变化就是有顺序,无变化就是无顺序.
变换元素的位置
例2某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛 题型2排列的简单应用要完成的“一件事”是什么?abcdef每2队之间需比赛2场a→主队,b→客队a→客队,b→主队要完成的“一件事”是否与“顺序”有关?主队、客队是否为排列问题?是排列从_____支队中选出_____支,____支作为______, ____支作为______例2某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛 如何用计数原理求出比赛场数?题型2排列的简单应用练习2:学校乒乓团体比赛采用5场3胜制(5场单打),每支球队派3名运动员参赛,前3场比赛每名运动员各出场1次,其中第1,2位出场的运动员在后2场比赛中还将各出场1次.(1)从5名运动员中选3名参加比赛,前3场比赛有几种出场情况 (2)甲、乙、丙3名运动员参加比赛,写出所有可能的出场情况.题型2排列的简单应用例3(1) 一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法 (2) 学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少 种不同的选法 追问(3):例3(1)是排列问题吗?追问(4):例3(2)是排列问题吗?不满足元素的互异性追问(1):这两个问题的不同点是什么?题型2排列的简单应用追问(2):是否有重复抽取同一元素的情况?是排列不是排列例3(1) 一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法 (2) 学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少 种不同的选法 题型2排列的简单应用追问(5):如何用计数原理求解?练习(1)有7本不同的书,从中选3本送给3名同学,每人各1本,共有多少种不同的取法 (2)有7种不同的书,要买3本送给3名同学,每人各1本,共有多少种不同的取法 题型2排列的简单应用
反思感悟
解决此类相似问题时,首先要分清楚是不是排列问题,其次使用分步乘法计数原理求排列总数时,要做到步骤完整,步与步之间相互独立,然后把完成每一步的方法数相乘即可得到总数. .
课堂小结
课堂小结一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).1.排列的定义:注意排列的两个关键要素:元素互异,元素按顺序排列.2.排列的简单计算:树状图分析、列举、分步乘法计数原理.
