说课稿---椭圆的简单几何性质(一)
文档属性
| 名称 | 说课稿---椭圆的简单几何性质(一) |
|
|
| 格式 | rar | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-12 00:00:00 | ||
图片预览

文档简介
课题:椭圆的简单几何性质(第一课时)
文昌华侨中学 林朝军
环 节 内 容 理论依据或意图
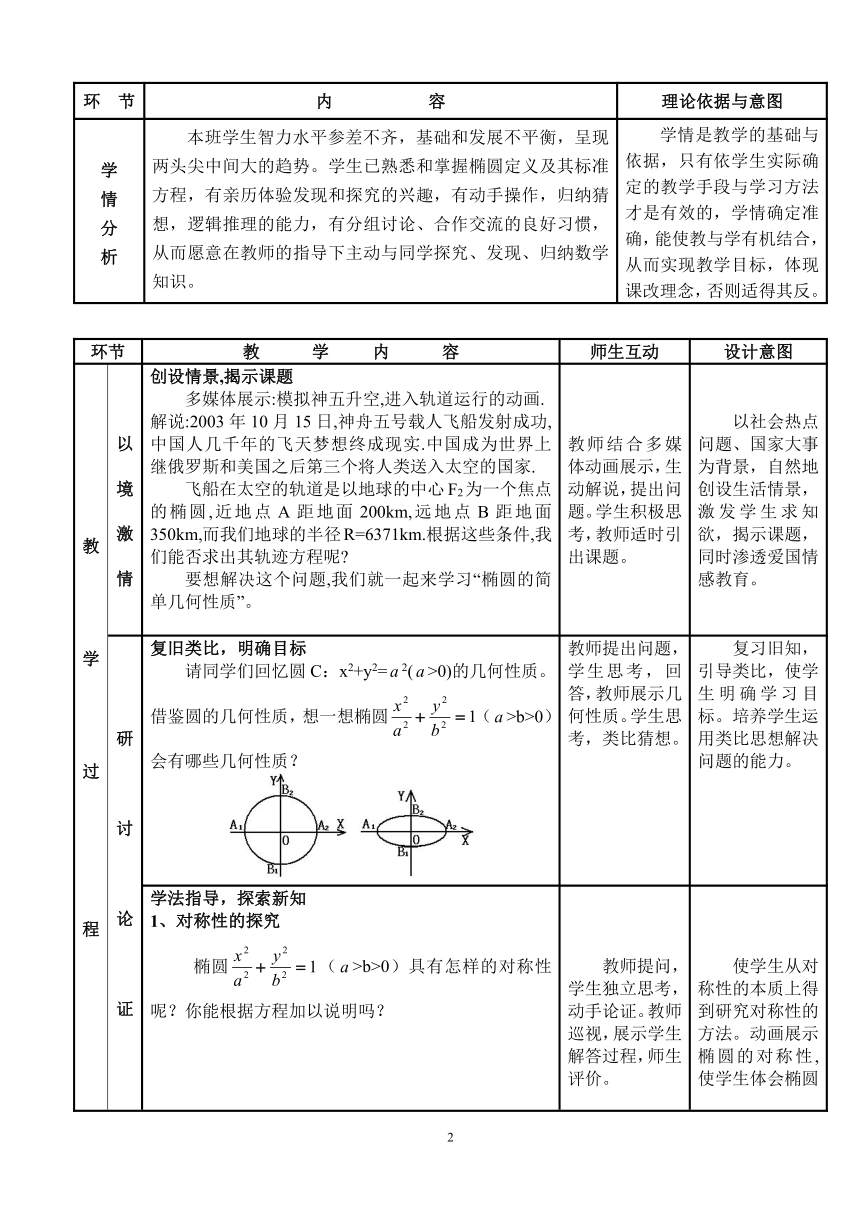
教材分析 教材地位与作用 “椭圆的简单几何性质”是人教A版高中实验教材选修2-1第二章第二节的内容。本节课是在学习了椭圆的定义及其标准方程的基础上,第一次系统地按照椭圆方程来研究椭圆的简单几何性质,为后面研究双曲线、抛物线的几何性质奠定了基础,是高中数学的重要内容,也是高考的重点与热点内容。该内容分两个课时教学,本节课是第一课时,主要内容是:探究椭圆的简单几何性质及应用。 《高中数学课程标准》
教学目标 1、知识与技能■ 探究椭圆的简单几何性质,初步学习利用方程研究曲线性质的方法。■ 掌握椭圆的简单几何性质,理解椭圆方程与椭圆曲线间互逆推导的逻辑关系及利用数形结合解决实际问题。2、过程与方法■ 通过椭圆的方程研究椭圆的简单几何性质,使学生经历知识产生与形成的过程,培养学生观察、分析、逻辑推理,理性思维的能力。■ 通过掌握椭圆的简单几何性质及应用过程,培养学生对研究方法的思想渗透及运用数形结合思想解决问题的能力。3、情感、态度与价值观通过数与形的辩证统一,对学生进行辩证唯物主义教育,通过对椭圆对称美的感受,激发学生对美好事物的追求。 根据《高中数学课程标准》的要求,强调积极主动,乐于探究,勤于动手,培养分析和解决问题的能力,逻辑推理及理性思维的能力,结合学生的实际情况确定的。
教学重难点 教学重点:椭圆的简单几何性质及其探究过程教学难点:利用曲线方程研究曲线几何性质的基本方法和离心率定义的给出过程。 本节课是围绕着探究椭圆的简单几何性质进行的。因此,依教材的地位与作用及教学目标,将之确定为本节课的重点;又因为学生第一次系统地按照椭圆方程来研究椭圆的简单几何性质,学生感到困难,且如何定义离心率,学生感到棘手,所以我将之确定为本节课的难点。
环 节 内 容 理论依据与意图
学情分析 本班学生智力水平参差不齐,基础和发展不平衡,呈现两头尖中间大的趋势。学生已熟悉和掌握椭圆定义及其标准方程,有亲历体验发现和探究的兴趣,有动手操作,归纳猜想,逻辑推理的能力,有分组讨论、合作交流的良好习惯,从而愿意在教师的指导下主动与同学探究、发现、归纳数学知识。 学情是教学的基础与依据,只有依学生实际确定的教学手段与学习方法才是有效的,学情确定准确,能使教与学有机结合,从而实现教学目标,体现课改理念,否则适得其反。
环节 教 学 内 容 师生互动 设计意图
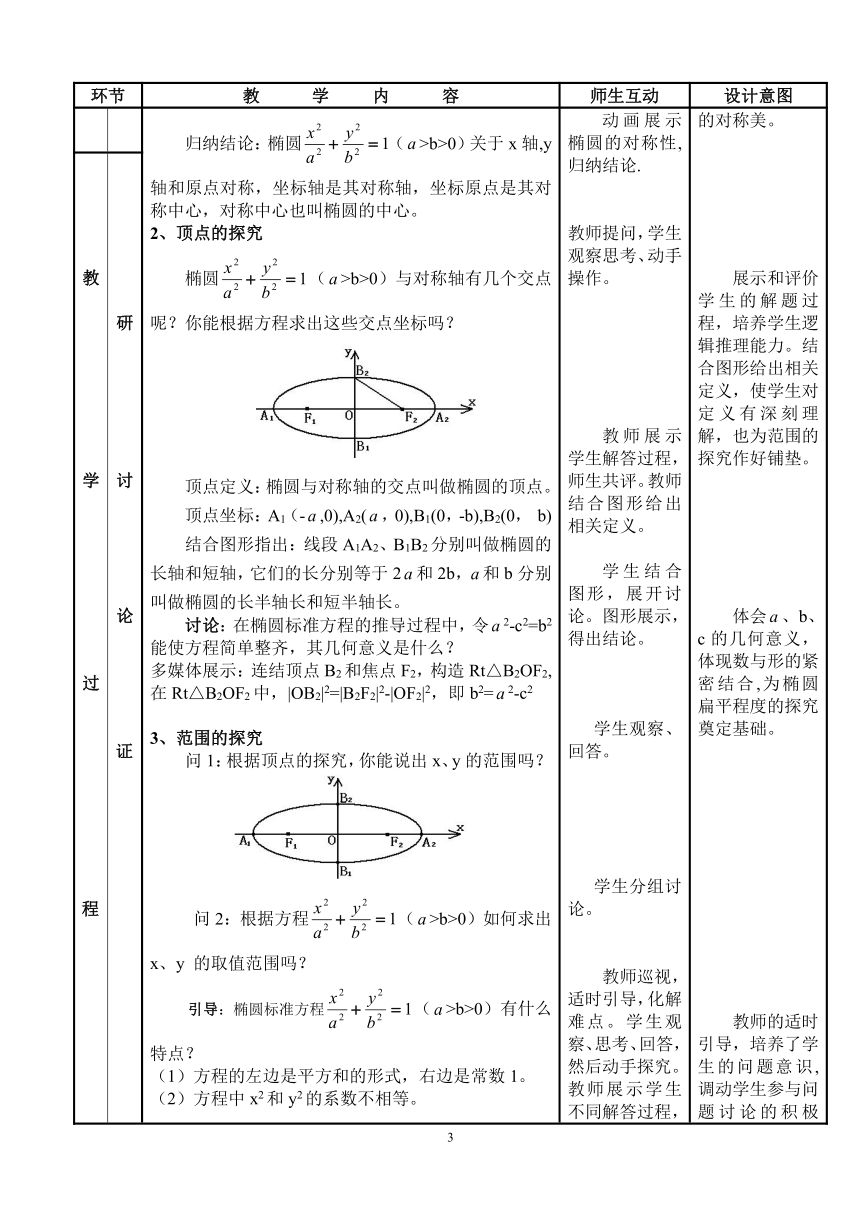
教学过程 以境激情 创设情景,揭示课题多媒体展示:模拟神五升空,进入轨道运行的动画.解说:2003年10月15日,神舟五号载人飞船发射成功,中国人几千年的飞天梦想终成现实.中国成为世界上继俄罗斯和美国之后第三个将人类送入太空的国家.飞船在太空的轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面200km,远地点B距地面350km,而我们地球的半径R=6371km.根据这些条件,我们能否求出其轨迹方程呢 要想解决这个问题,我们就一起来学习“椭圆的简单几何性质”。 教师结合多媒体动画展示,生动解说,提出问题。学生积极思考,教师适时引出课题。 以社会热点问题、国家大事为背景,自然地创设生活情景,激发学生求知欲,揭示课题,同时渗透爱国情感教育。
研讨论证 复旧类比,明确目标请同学们回忆圆C:x2+y2=2(>0)的几何性质。借鉴圆的几何性质,想一想椭圆(>b>0)会有哪些几何性质? 教师提出问题,学生思考,回答,教师展示几何性质。学生思考,类比猜想。 复习旧知,引导类比,使学生明确学习目标。培养学生运用类比思想解决问题的能力。
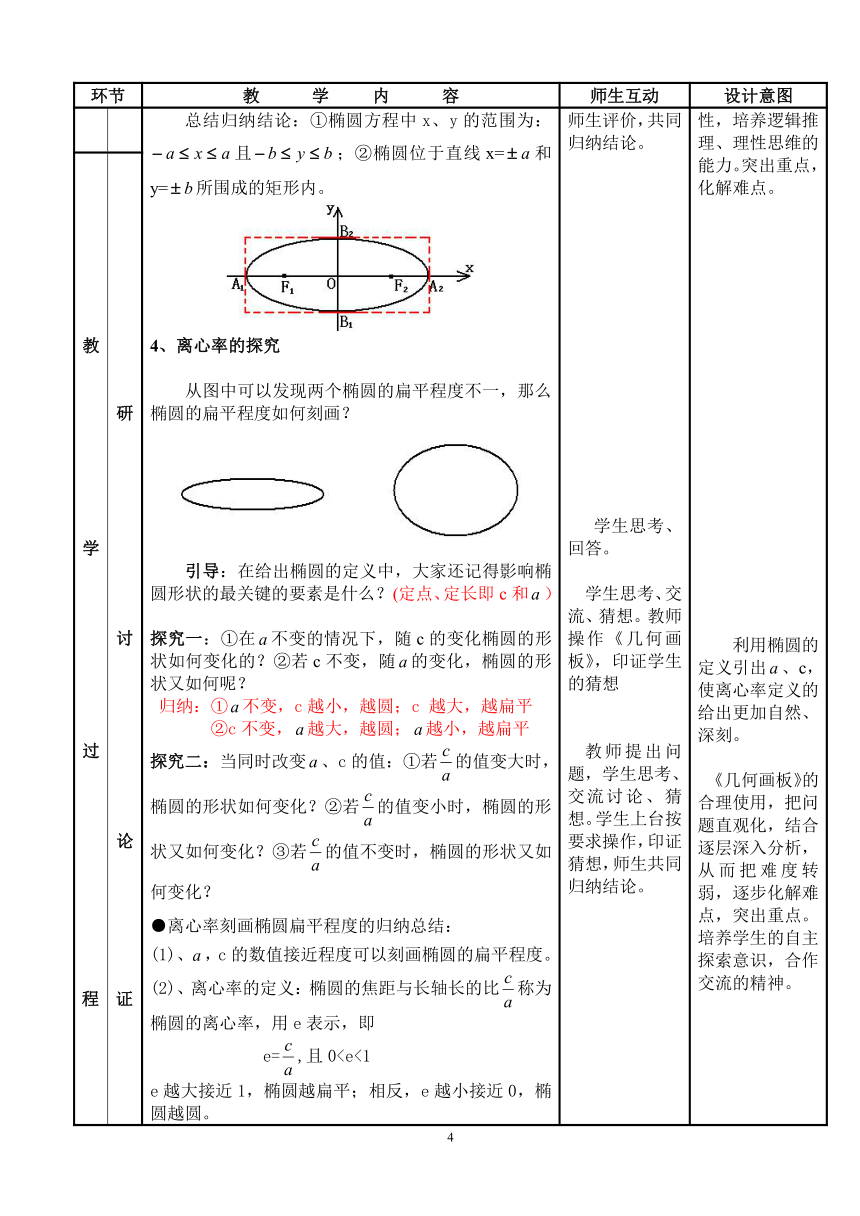
学法指导,探索新知1、对称性的探究 椭圆(>b>0)具有怎样的对称性呢?你能根据方程加以说明吗?归纳结论:椭圆(>b>0)关于x轴,y轴和原点对称,坐标轴是其对称轴,坐标原点是其对称中心,对称中心也叫椭圆的中心。2、顶点的探究椭圆(>b>0)与对称轴有几个交点呢?你能根据方程求出这些交点坐标吗?顶点定义:椭圆与对称轴的交点叫做椭圆的顶点。顶点坐标:A1(-,0),A2(,0),B1(0,-b),B2(0, b)结合图形指出:线段A1A2、B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2和2b,和b分别叫做椭圆的长半轴长和短半轴长。讨论:在椭圆标准方程的推导过程中,令2-c2=b2能使方程简单整齐,其几何意义是什么?多媒体展示:连结顶点B2和焦点F2,构造Rt△B2OF2,在Rt△B2OF2中,|OB2|2=|B2F2|2-|OF2|2,即b2=2-c23、范围的探究问1:根据顶点的探究,你能说出x、y的范围吗? 问2:根据方程(>b>0)如何求出x、y 的取值范围吗?引导:椭圆标准方程(>b>0)有什么特点?(1)方程的左边是平方和的形式,右边是常数1。(2)方程中x2和y2的系数不相等。总结归纳结论:①椭圆方程中x、y的范围为: 且;②椭圆位于直线x=和y=所围成的矩形内。4、离心率的探究从图中可以发现两个椭圆的扁平程度不一,那么椭圆的扁平程度如何刻画?引导:在给出椭圆的定义中,大家还记得影响椭圆形状的最关键的要素是什么?(定点、定长即c和)探究一:①在不变的情况下,随c的变化椭圆的形状如何变化的?②若c不变,随的变化,椭圆的形状又如何呢?归纳:①不变,c越小,越圆;c 越大,越扁平②c不变,越大,越圆;越小,越扁平探究二:当同时改变、c的值:①若的值变大时,椭圆的形状如何变化?②若的值变小时,椭圆的形状又如何变化?③若的值不变时,椭圆的形状又如何变化?●离心率刻画椭圆扁平程度的归纳总结:(1)、,c的数值接近程度可以刻画椭圆的扁平程度。(2)、离心率的定义:椭圆的焦距与长轴长的比称为椭圆的离心率,用e表示,即 e=,且0教学过程教学过程教学过程教学过程 研讨论证研讨论证研讨论证
深化提高深化提高 应用举例例4、若椭圆方程为16x2+25y2=400。(1)求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标。(2)画出该椭圆的草图。 学生思考。教师引导学生找出解决问题的关键。学生动手操作,展示学生的解答过程,师生评价,共同归纳作图步骤及注意点。 学生及时巩固新知识,掌握椭圆的几何性质及椭圆草图作图方法。
例5、 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分。灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上。由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2。已知BC⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm)。 学生分组讨论。教师引导学生建立适当直角坐标系。学生思考、交流、讨论,写出解答过程。展示解答过程,教师评价分析,引导归纳建立适当直角坐标系的原则。 提高学生分析问题,运用几何性质、数形结合思想解决实际问题的能力,感受建立适当直角坐标系的原则。
巩固练习1、若椭圆的方程为2x2+y2=8。①求椭圆的长轴和短轴长,离心率、焦点坐标、顶点坐标和x、y的范围。②画出椭圆的草图。2、若椭圆焦点在x轴上, e=,右焦点到右顶点的距离为4,求椭圆的标准方程。3、比较下列每组中椭圆的形状,哪一个更圆,哪一个更扁?为什么?①② 学生独立思考,同桌之间交流,动手操作。教师巡视,展示学生解答过程,师生共评。 学生及时巩固新知识,掌握椭圆的简单几何性质和椭圆扁平程度的刻画方法。培养学生解决问题的能力。
应用实践如图所示,“神舟”载人飞船在太空的轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面200km,远地点B距地面350km,已知地球的半径R=6371km.建立适当的直角坐标系,求出椭圆的轨迹方程。 教师巡视引导启发、学生分组讨论,找出已知条件,转化条件,寻求解决方法。 首尾呼应,运用所学知识解决实际问题。加强学生分析问题,运用数形结合思想解决实际问题的能力。
总结评价 小结: 教师通过多媒体展示,提出问题,学生思考回答,师生共同小结。 利用“教学流程图”形式简明地对本节课的重点内容进行学习层级方面的展示,以达到促进学生数学知识保持和迁移目的。
作业布置: P49 习题2.2 A组3、9 巩固知识,及时反馈教学信息,加强“双基”训练。
环 节 教 学 内 容 设 计 意 图
教学过程 板书设计 有利于学生对本节课的知识有一个系统的认识.
环节 内 容 理论依据或意图
教法分析 本节课以启发式教学为主,综合运用演示法、讲授法、讨论法、有指导的发现法及练习法等教学方法。先通过多媒体动画演示,创设问题情境;在椭圆简单几何性质的教学过程中,通过多媒体演示,有指导的发现问题,然后进行讨论、探究、总结、运用,最后通过练习加以巩固提高。 引导启发式教学是课堂教学的重要手段,是体现课改理念的一种主要方式。学生通过教师的引导,发现问题,猜想、论证归纳并解决问题,使学生感受知识形式过程,从而实现“三维”教学目标。
学法分析 根据本节课特点,结合教法和学生的实际,在多媒体辅助教学的基础上,主要采用“观察——猜想——论证——归纳——应用”的探究式学习方法,增加学生参与的机会,使学生在掌握知识形成技能的同时,培养逻辑推理、理性思维的能力及科学的学习方法,增强自信心。 探究式学习方式是现代课堂教学主要的常见模式,依本节内容特点,在本班学生实际情况教学下确定,学生在教师引导启发下通过师生共同探究活动,让学生感受知识形成过程,从而实现“三维”教学目标。
评价分析 本节课在教学设计上,力求调动一切积极因素,激发学生的学习兴趣。在教师的引导启发下,使学生的思维围绕“探究”步步深入,最大限度挖掘学生潜能,体现学生的主体性。我认为本节课达到如下教学效果:■ “生活情景”激发学生学习的兴趣,椭圆简单几何性质的探究过程增强了学生的自信心和感受研究方法的思想渗透。■ 通过动手操作,合作交流,使学生发现并掌握椭圆的简单几何性质,感受领会从数到形的探究过程。■ 椭圆简单几何性质的应用(如例题、练习)培养了学生分析、抽象、概括、逻辑推理的能力和运用数形结合思想解决实际问题的能力。■ 整个课堂设计关注学生个体差异,使不同的个体均获得不同程度的学习效果和收获。 评价分析是由教学过程的反馈,检验教学是否达到预期目的,教学目标是否实现,教学方法与手段运用是否恰当的一个重要环节。一个方面,它可以了解学生对知识掌握能力培养的程度;另一方面,它又为以后的教学构想调整与教学措施的设计提供依据。
PAGE
3
文昌华侨中学 林朝军
环 节 内 容 理论依据或意图
教材分析 教材地位与作用 “椭圆的简单几何性质”是人教A版高中实验教材选修2-1第二章第二节的内容。本节课是在学习了椭圆的定义及其标准方程的基础上,第一次系统地按照椭圆方程来研究椭圆的简单几何性质,为后面研究双曲线、抛物线的几何性质奠定了基础,是高中数学的重要内容,也是高考的重点与热点内容。该内容分两个课时教学,本节课是第一课时,主要内容是:探究椭圆的简单几何性质及应用。 《高中数学课程标准》
教学目标 1、知识与技能■ 探究椭圆的简单几何性质,初步学习利用方程研究曲线性质的方法。■ 掌握椭圆的简单几何性质,理解椭圆方程与椭圆曲线间互逆推导的逻辑关系及利用数形结合解决实际问题。2、过程与方法■ 通过椭圆的方程研究椭圆的简单几何性质,使学生经历知识产生与形成的过程,培养学生观察、分析、逻辑推理,理性思维的能力。■ 通过掌握椭圆的简单几何性质及应用过程,培养学生对研究方法的思想渗透及运用数形结合思想解决问题的能力。3、情感、态度与价值观通过数与形的辩证统一,对学生进行辩证唯物主义教育,通过对椭圆对称美的感受,激发学生对美好事物的追求。 根据《高中数学课程标准》的要求,强调积极主动,乐于探究,勤于动手,培养分析和解决问题的能力,逻辑推理及理性思维的能力,结合学生的实际情况确定的。
教学重难点 教学重点:椭圆的简单几何性质及其探究过程教学难点:利用曲线方程研究曲线几何性质的基本方法和离心率定义的给出过程。 本节课是围绕着探究椭圆的简单几何性质进行的。因此,依教材的地位与作用及教学目标,将之确定为本节课的重点;又因为学生第一次系统地按照椭圆方程来研究椭圆的简单几何性质,学生感到困难,且如何定义离心率,学生感到棘手,所以我将之确定为本节课的难点。
环 节 内 容 理论依据与意图
学情分析 本班学生智力水平参差不齐,基础和发展不平衡,呈现两头尖中间大的趋势。学生已熟悉和掌握椭圆定义及其标准方程,有亲历体验发现和探究的兴趣,有动手操作,归纳猜想,逻辑推理的能力,有分组讨论、合作交流的良好习惯,从而愿意在教师的指导下主动与同学探究、发现、归纳数学知识。 学情是教学的基础与依据,只有依学生实际确定的教学手段与学习方法才是有效的,学情确定准确,能使教与学有机结合,从而实现教学目标,体现课改理念,否则适得其反。
环节 教 学 内 容 师生互动 设计意图
教学过程 以境激情 创设情景,揭示课题多媒体展示:模拟神五升空,进入轨道运行的动画.解说:2003年10月15日,神舟五号载人飞船发射成功,中国人几千年的飞天梦想终成现实.中国成为世界上继俄罗斯和美国之后第三个将人类送入太空的国家.飞船在太空的轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面200km,远地点B距地面350km,而我们地球的半径R=6371km.根据这些条件,我们能否求出其轨迹方程呢 要想解决这个问题,我们就一起来学习“椭圆的简单几何性质”。 教师结合多媒体动画展示,生动解说,提出问题。学生积极思考,教师适时引出课题。 以社会热点问题、国家大事为背景,自然地创设生活情景,激发学生求知欲,揭示课题,同时渗透爱国情感教育。
研讨论证 复旧类比,明确目标请同学们回忆圆C:x2+y2=2(>0)的几何性质。借鉴圆的几何性质,想一想椭圆(>b>0)会有哪些几何性质? 教师提出问题,学生思考,回答,教师展示几何性质。学生思考,类比猜想。 复习旧知,引导类比,使学生明确学习目标。培养学生运用类比思想解决问题的能力。
学法指导,探索新知1、对称性的探究 椭圆(>b>0)具有怎样的对称性呢?你能根据方程加以说明吗?归纳结论:椭圆(>b>0)关于x轴,y轴和原点对称,坐标轴是其对称轴,坐标原点是其对称中心,对称中心也叫椭圆的中心。2、顶点的探究椭圆(>b>0)与对称轴有几个交点呢?你能根据方程求出这些交点坐标吗?顶点定义:椭圆与对称轴的交点叫做椭圆的顶点。顶点坐标:A1(-,0),A2(,0),B1(0,-b),B2(0, b)结合图形指出:线段A1A2、B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2和2b,和b分别叫做椭圆的长半轴长和短半轴长。讨论:在椭圆标准方程的推导过程中,令2-c2=b2能使方程简单整齐,其几何意义是什么?多媒体展示:连结顶点B2和焦点F2,构造Rt△B2OF2,在Rt△B2OF2中,|OB2|2=|B2F2|2-|OF2|2,即b2=2-c23、范围的探究问1:根据顶点的探究,你能说出x、y的范围吗? 问2:根据方程(>b>0)如何求出x、y 的取值范围吗?引导:椭圆标准方程(>b>0)有什么特点?(1)方程的左边是平方和的形式,右边是常数1。(2)方程中x2和y2的系数不相等。总结归纳结论:①椭圆方程中x、y的范围为: 且;②椭圆位于直线x=和y=所围成的矩形内。4、离心率的探究从图中可以发现两个椭圆的扁平程度不一,那么椭圆的扁平程度如何刻画?引导:在给出椭圆的定义中,大家还记得影响椭圆形状的最关键的要素是什么?(定点、定长即c和)探究一:①在不变的情况下,随c的变化椭圆的形状如何变化的?②若c不变,随的变化,椭圆的形状又如何呢?归纳:①不变,c越小,越圆;c 越大,越扁平②c不变,越大,越圆;越小,越扁平探究二:当同时改变、c的值:①若的值变大时,椭圆的形状如何变化?②若的值变小时,椭圆的形状又如何变化?③若的值不变时,椭圆的形状又如何变化?●离心率刻画椭圆扁平程度的归纳总结:(1)、,c的数值接近程度可以刻画椭圆的扁平程度。(2)、离心率的定义:椭圆的焦距与长轴长的比称为椭圆的离心率,用e表示,即 e=,且0
深化提高深化提高 应用举例例4、若椭圆方程为16x2+25y2=400。(1)求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标。(2)画出该椭圆的草图。 学生思考。教师引导学生找出解决问题的关键。学生动手操作,展示学生的解答过程,师生评价,共同归纳作图步骤及注意点。 学生及时巩固新知识,掌握椭圆的几何性质及椭圆草图作图方法。
例5、 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分。灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上。由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2。已知BC⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm)。 学生分组讨论。教师引导学生建立适当直角坐标系。学生思考、交流、讨论,写出解答过程。展示解答过程,教师评价分析,引导归纳建立适当直角坐标系的原则。 提高学生分析问题,运用几何性质、数形结合思想解决实际问题的能力,感受建立适当直角坐标系的原则。
巩固练习1、若椭圆的方程为2x2+y2=8。①求椭圆的长轴和短轴长,离心率、焦点坐标、顶点坐标和x、y的范围。②画出椭圆的草图。2、若椭圆焦点在x轴上, e=,右焦点到右顶点的距离为4,求椭圆的标准方程。3、比较下列每组中椭圆的形状,哪一个更圆,哪一个更扁?为什么?①② 学生独立思考,同桌之间交流,动手操作。教师巡视,展示学生解答过程,师生共评。 学生及时巩固新知识,掌握椭圆的简单几何性质和椭圆扁平程度的刻画方法。培养学生解决问题的能力。
应用实践如图所示,“神舟”载人飞船在太空的轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面200km,远地点B距地面350km,已知地球的半径R=6371km.建立适当的直角坐标系,求出椭圆的轨迹方程。 教师巡视引导启发、学生分组讨论,找出已知条件,转化条件,寻求解决方法。 首尾呼应,运用所学知识解决实际问题。加强学生分析问题,运用数形结合思想解决实际问题的能力。
总结评价 小结: 教师通过多媒体展示,提出问题,学生思考回答,师生共同小结。 利用“教学流程图”形式简明地对本节课的重点内容进行学习层级方面的展示,以达到促进学生数学知识保持和迁移目的。
作业布置: P49 习题2.2 A组3、9 巩固知识,及时反馈教学信息,加强“双基”训练。
环 节 教 学 内 容 设 计 意 图
教学过程 板书设计 有利于学生对本节课的知识有一个系统的认识.
环节 内 容 理论依据或意图
教法分析 本节课以启发式教学为主,综合运用演示法、讲授法、讨论法、有指导的发现法及练习法等教学方法。先通过多媒体动画演示,创设问题情境;在椭圆简单几何性质的教学过程中,通过多媒体演示,有指导的发现问题,然后进行讨论、探究、总结、运用,最后通过练习加以巩固提高。 引导启发式教学是课堂教学的重要手段,是体现课改理念的一种主要方式。学生通过教师的引导,发现问题,猜想、论证归纳并解决问题,使学生感受知识形式过程,从而实现“三维”教学目标。
学法分析 根据本节课特点,结合教法和学生的实际,在多媒体辅助教学的基础上,主要采用“观察——猜想——论证——归纳——应用”的探究式学习方法,增加学生参与的机会,使学生在掌握知识形成技能的同时,培养逻辑推理、理性思维的能力及科学的学习方法,增强自信心。 探究式学习方式是现代课堂教学主要的常见模式,依本节内容特点,在本班学生实际情况教学下确定,学生在教师引导启发下通过师生共同探究活动,让学生感受知识形成过程,从而实现“三维”教学目标。
评价分析 本节课在教学设计上,力求调动一切积极因素,激发学生的学习兴趣。在教师的引导启发下,使学生的思维围绕“探究”步步深入,最大限度挖掘学生潜能,体现学生的主体性。我认为本节课达到如下教学效果:■ “生活情景”激发学生学习的兴趣,椭圆简单几何性质的探究过程增强了学生的自信心和感受研究方法的思想渗透。■ 通过动手操作,合作交流,使学生发现并掌握椭圆的简单几何性质,感受领会从数到形的探究过程。■ 椭圆简单几何性质的应用(如例题、练习)培养了学生分析、抽象、概括、逻辑推理的能力和运用数形结合思想解决实际问题的能力。■ 整个课堂设计关注学生个体差异,使不同的个体均获得不同程度的学习效果和收获。 评价分析是由教学过程的反馈,检验教学是否达到预期目的,教学目标是否实现,教学方法与手段运用是否恰当的一个重要环节。一个方面,它可以了解学生对知识掌握能力培养的程度;另一方面,它又为以后的教学构想调整与教学措施的设计提供依据。
PAGE
3
