2014年湖南省高中学业水平考试数学真题(精校版,含答案)
文档属性
| 名称 | 2014年湖南省高中学业水平考试数学真题(精校版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 186.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-19 13:25:55 | ||
图片预览

文档简介
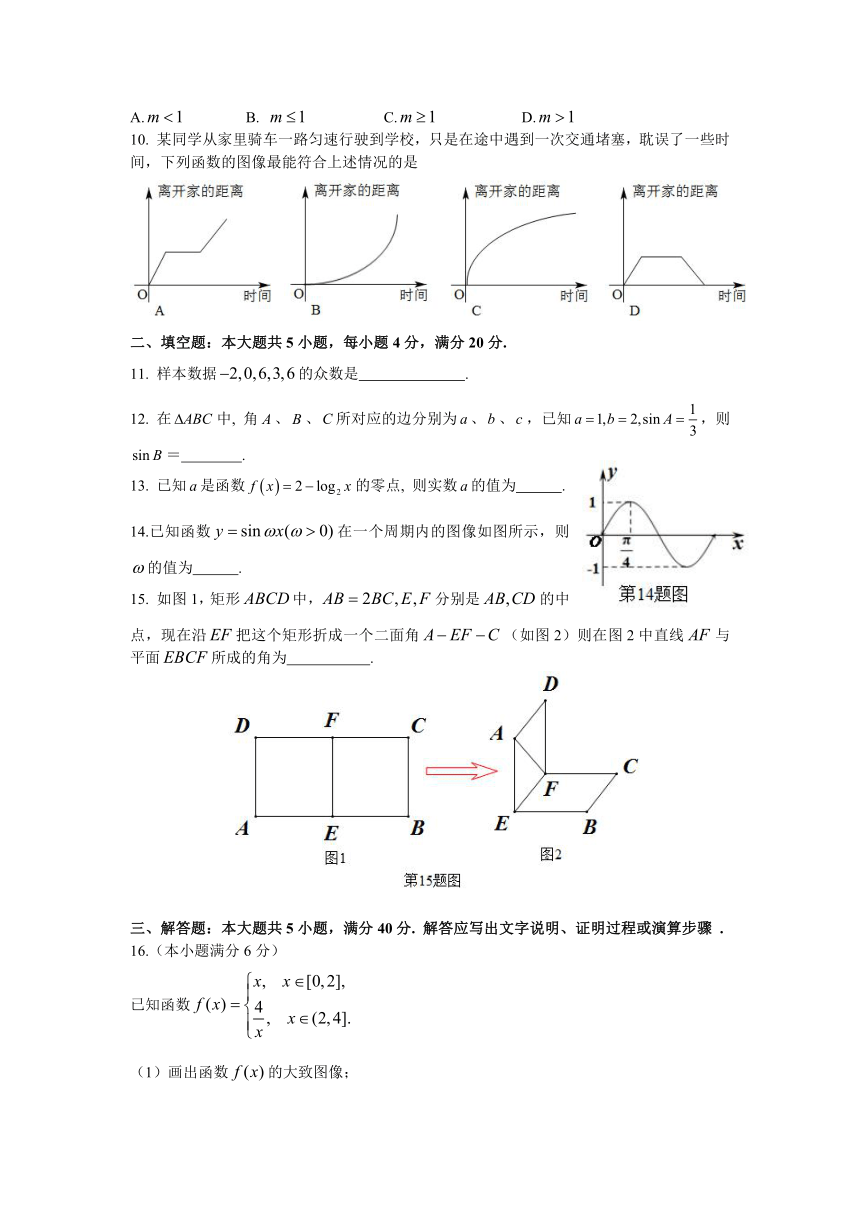
2014年湖南省普通高中学业水平考试试卷
数 学
本试卷包括选择题、填空题和解答题三部分,共5页
时量120分钟,满分100分.
一、选择题:本大题共10小题,每小题4分,满分40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图是一个几何体的三视图,则该几何体为
A.圆柱 B.圆锥
C.圆台 D.球
2.已知元素,且,则的值为
A.0 B.1 C.2 D.3
3.在区间内任取一个实数,则此数大于3的概率为
A. B.
C. D.
4.某程序框图如图所示,若输入的值为1,则输出的值是
A.2 B.3 C.4 D.5
5.在△中,若,则△的形状是
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
6.的值为
A. B. C. D.
7.如图,在正方体中,异面直线与的位置关系是
A.平行 B.相交 C.异面但不垂直 D. 异面且垂直
8.不等式的解集为
A. B.
C. D.
9.点不在不等式表示的平面区域内,则实数的取值范围是
A. B. C. D.
10. 某同学从家里骑车一路匀速行驶到学校,只是在途中遇到一次交通堵塞,耽误了一些时间,下列函数的图像最能符合上述情况的是
( http: / / www.21cnjy.com )
二、填空题:本大题共5小题,每小题4分,满分20分.
11. 样本数据的众数是 .
12. 在中, 角、、所对应的边分别为、、,已知,则= .
13. 已知是函数的零点, 则实数的值为 .
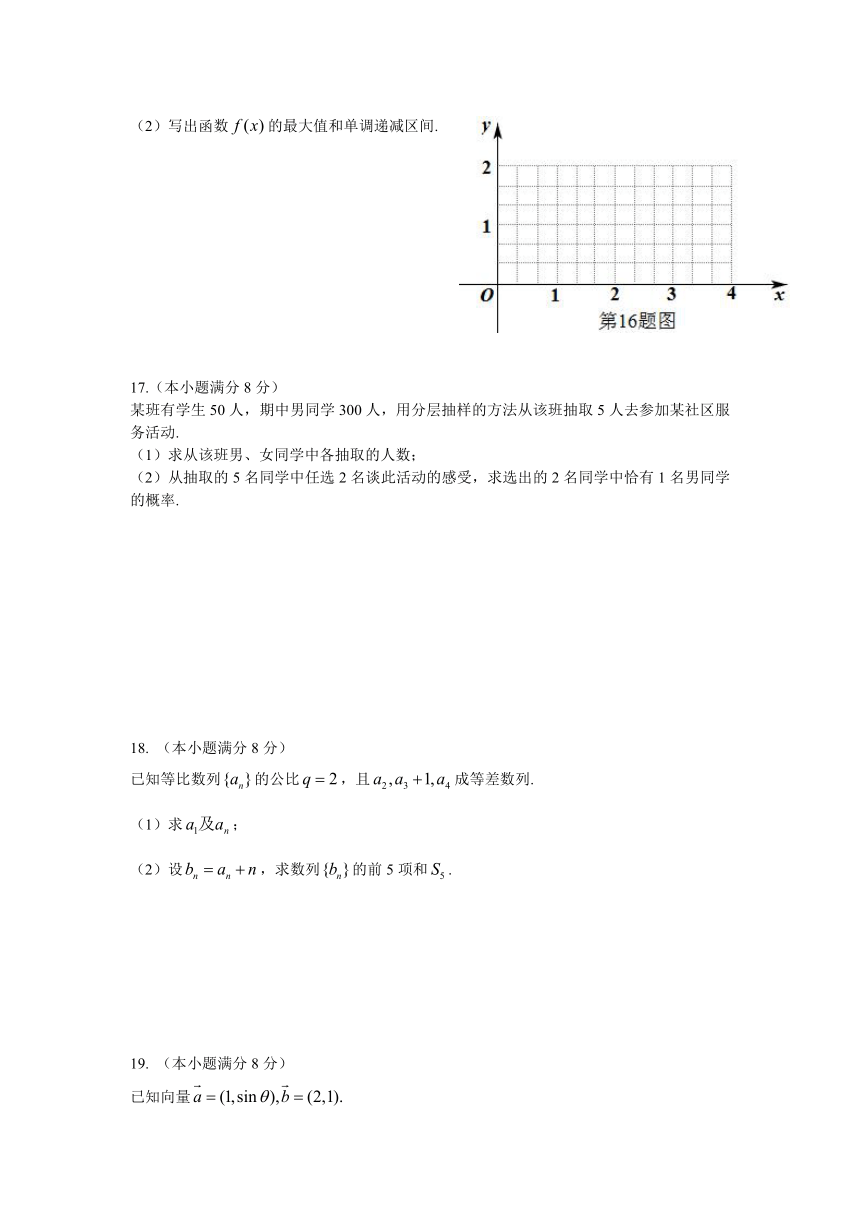
14.已知函数在一个周期内的图像如图所示,则的值为 .
15. 如图1,矩形中,分别是的中点,现在沿把这个矩形折成一个二面角(如图2)则在图2中直线与平面所成的角为 .
三、解答题:本大题共5小题,满分40分. 解答应写出文字说明、证明过程或演算步骤 .
16.(本小题满分6分)
已知函数
(1)画出函数的大致图像;
(2)写出函数的最大值和单调递减区间.
17.(本小题满分8分)
某班有学生50人,期中男同学300人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.
(1)求从该班男、女同学中各抽取的人数;
(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率.
18. (本小题满分8分)
已知等比数列的公比,且成等差数列.
(1)求;
(2)设,求数列的前5项和.
19. (本小题满分8分)
已知向量
(1)当时,求向量的坐标;
(2)若∥,且,求的值.
20. (本小题满分10分)
已知圆.
(1)求圆的圆心的坐标和半径长;
(2)直线经过坐标原点且不与轴重合,与圆相交于两点,求证:为定值;
(3)斜率为1的直线与圆相交于两点,求直线的方程,使△CDE的面积最大.
2014年湖南省普通高中学业水平考试数学试卷
参考答案及评分标准
一、选择题(每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B A C D A C A
二 、填空题(每小题4分,满分20分)
11.6 12. 13.4 14.2 15. (或)
三 、解答题(满分40分)
16. 解:(1)函数的大致图象如图所示; ……………………………2分
(2)由函数的图象得出,
的最大值为2, ………………4分
其单调递减区间为.…………6分
17. 解: (1)(人), (人),
所以从男同学中抽取3人, 女同学中抽取2人; ……………………………………4分
(2)过程略.
. ……………………………………………………………………………8分
18. 解: (1); ………………………………………………………………4分
(2). ……………………………………………………………………………8分
19. 解: (1); …………………………………………………………………4分
(2). ………………………………………………………………………8分
20. 解: (1)配方得, 则圆心C的坐标为,……………………2分
圆的半径长为; ………………………………………………………………………4分
(2)设直线的方程为,
联立方程组,
消去得, ………………………………………………5分
则有: ………………………………………………6分
所以为定值. ………………………………………………7分
(3)解法一 设直线m的方程为, 则圆心C到直线m的距离
, 所以, …………………………………8分
,
当且仅当,即时, 的面积最大, …………………………9分
从而, 解之得或,
故所求直线方程为或.……………………………………10分
解法二 由(1)知,
所以,当且仅当时, 的面积最大, 此时, ………………………………………………………8分
设直线m的方程为
则圆心C到直线m的距离,…………………………………………………9分
由, 得,
由,得或,
故所求直线方程为或.……………………………………10分
数 学
本试卷包括选择题、填空题和解答题三部分,共5页
时量120分钟,满分100分.
一、选择题:本大题共10小题,每小题4分,满分40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图是一个几何体的三视图,则该几何体为
A.圆柱 B.圆锥
C.圆台 D.球
2.已知元素,且,则的值为
A.0 B.1 C.2 D.3
3.在区间内任取一个实数,则此数大于3的概率为
A. B.
C. D.
4.某程序框图如图所示,若输入的值为1,则输出的值是
A.2 B.3 C.4 D.5
5.在△中,若,则△的形状是
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
6.的值为
A. B. C. D.
7.如图,在正方体中,异面直线与的位置关系是
A.平行 B.相交 C.异面但不垂直 D. 异面且垂直
8.不等式的解集为
A. B.
C. D.
9.点不在不等式表示的平面区域内,则实数的取值范围是
A. B. C. D.
10. 某同学从家里骑车一路匀速行驶到学校,只是在途中遇到一次交通堵塞,耽误了一些时间,下列函数的图像最能符合上述情况的是
( http: / / www.21cnjy.com )
二、填空题:本大题共5小题,每小题4分,满分20分.
11. 样本数据的众数是 .
12. 在中, 角、、所对应的边分别为、、,已知,则= .
13. 已知是函数的零点, 则实数的值为 .
14.已知函数在一个周期内的图像如图所示,则的值为 .
15. 如图1,矩形中,分别是的中点,现在沿把这个矩形折成一个二面角(如图2)则在图2中直线与平面所成的角为 .
三、解答题:本大题共5小题,满分40分. 解答应写出文字说明、证明过程或演算步骤 .
16.(本小题满分6分)
已知函数
(1)画出函数的大致图像;
(2)写出函数的最大值和单调递减区间.
17.(本小题满分8分)
某班有学生50人,期中男同学300人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.
(1)求从该班男、女同学中各抽取的人数;
(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率.
18. (本小题满分8分)
已知等比数列的公比,且成等差数列.
(1)求;
(2)设,求数列的前5项和.
19. (本小题满分8分)
已知向量
(1)当时,求向量的坐标;
(2)若∥,且,求的值.
20. (本小题满分10分)
已知圆.
(1)求圆的圆心的坐标和半径长;
(2)直线经过坐标原点且不与轴重合,与圆相交于两点,求证:为定值;
(3)斜率为1的直线与圆相交于两点,求直线的方程,使△CDE的面积最大.
2014年湖南省普通高中学业水平考试数学试卷
参考答案及评分标准
一、选择题(每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B A C D A C A
二 、填空题(每小题4分,满分20分)
11.6 12. 13.4 14.2 15. (或)
三 、解答题(满分40分)
16. 解:(1)函数的大致图象如图所示; ……………………………2分
(2)由函数的图象得出,
的最大值为2, ………………4分
其单调递减区间为.…………6分
17. 解: (1)(人), (人),
所以从男同学中抽取3人, 女同学中抽取2人; ……………………………………4分
(2)过程略.
. ……………………………………………………………………………8分
18. 解: (1); ………………………………………………………………4分
(2). ……………………………………………………………………………8分
19. 解: (1); …………………………………………………………………4分
(2). ………………………………………………………………………8分
20. 解: (1)配方得, 则圆心C的坐标为,……………………2分
圆的半径长为; ………………………………………………………………………4分
(2)设直线的方程为,
联立方程组,
消去得, ………………………………………………5分
则有: ………………………………………………6分
所以为定值. ………………………………………………7分
(3)解法一 设直线m的方程为, 则圆心C到直线m的距离
, 所以, …………………………………8分
,
当且仅当,即时, 的面积最大, …………………………9分
从而, 解之得或,
故所求直线方程为或.……………………………………10分
解法二 由(1)知,
所以,当且仅当时, 的面积最大, 此时, ………………………………………………………8分
设直线m的方程为
则圆心C到直线m的距离,…………………………………………………9分
由, 得,
由,得或,
故所求直线方程为或.……………………………………10分
同课章节目录
