八年级数学下册试题 一次函数(基础练习)-沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 一次函数(基础练习)-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 12:09:42 | ||
图片预览



文档简介
一次函数(基础练习)
一、单选题
1.下列函数中,y是x的一次函数的是( )
①y=x﹣6;②y=;③y=;④y=7﹣x.
A.①②③ B.①③④ C.①②③④ D.②③④
2.若直线y=2x+b经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的是( )
A.m<n B.m>n C.m=n D.无法确定
3.点P1(x1,y1),点P2(x2,y2)是一次函数y=4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
4.y=2x|m|+3表示一次函数,则m等于( )
A.1 B.﹣1 C.0或﹣1 D.1或﹣1
5.若直线y=kx+b(k≠0)经过点A(2,﹣3),且与y轴的交点在x轴上方,则k的取值范围是( )
A.k> B.k>﹣ C.k<﹣ D.k<
6.如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法:
①甲比乙提前12分钟到达;
②甲的平均速度为15千米/小时;
③甲、乙相遇时,乙走了6千米;
④乙出发6分钟后追上甲,其中正确的是( )
A.①② B.③④ C.①③④ D.②③④
二、填空题
7.已知函数y=(n+3)x|n|﹣2是一次函数,则n= .
8.下列函数(1)y=3πx;(2)y=8x﹣6;(3)y=;(4)y=﹣8x;(5)y=5x2﹣4x+1中,是一次函数的有 .
9.将直线y=2x+4向下平移3个单位,则得到的新直线的解析式为 .
10.若正比例函数y=﹣2x的图象经过点A(a﹣1,4),则a的值是 ﹣ .
11.把直线y=2x﹣1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为 .
12.对于函数y=3x﹣6,当x=﹣2时,y= ﹣ ,当y=6时,x= .
13.函数:①y=﹣2x+3;②x+y=1;③xy=1;④y=;⑤y=+1;⑥y=0.5x中,属于一次函数的有 ,属正比例函数的有 (只填序号)
14.若一次函数y=ax+b(a≠0)的图象经过(3,2)和(﹣3,﹣1)两点,则方程ax+b=﹣1的解为 .
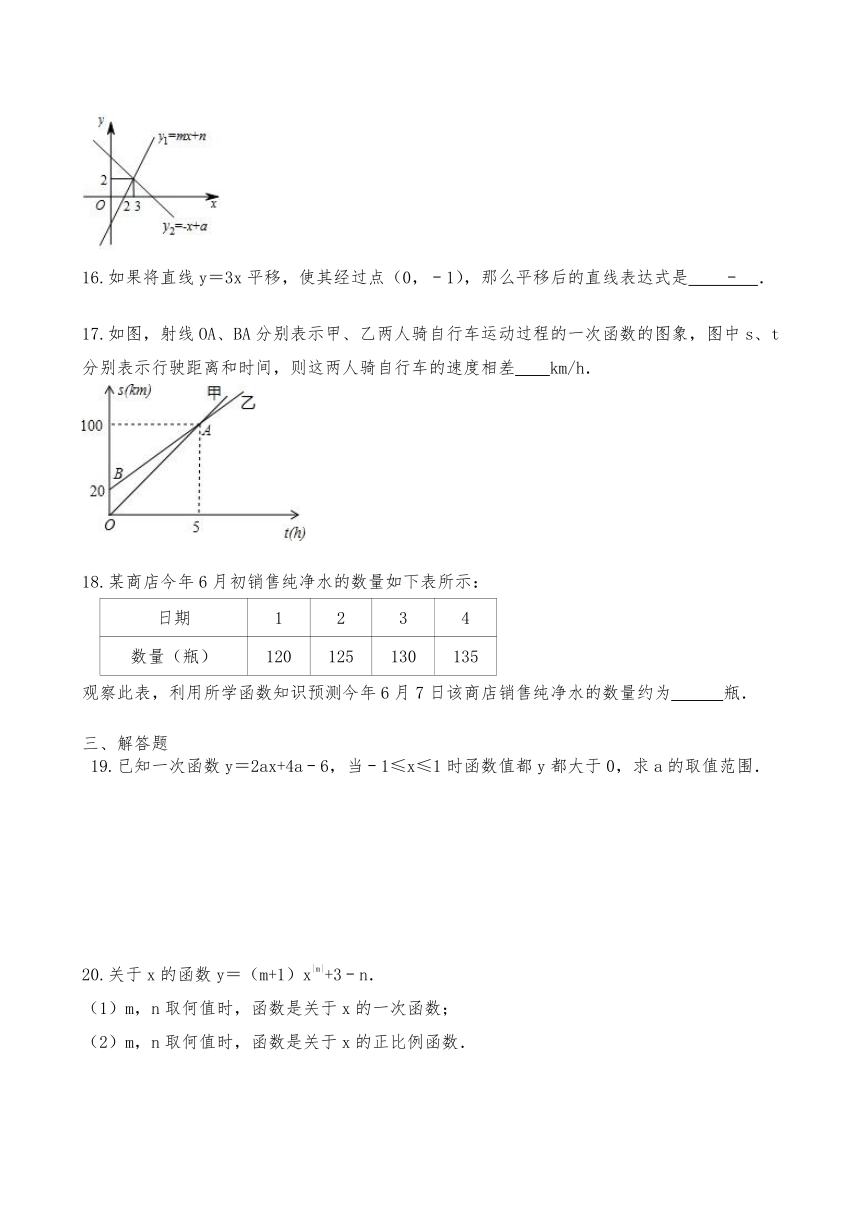
15.一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则0<mx+n<﹣x+a的解集为 .
16.如果将直线y=3x平移,使其经过点(0,﹣1),那么平移后的直线表达式是 ﹣ .
17.如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
18.某商店今年6月初销售纯净水的数量如下表所示:
日期 1 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
三、解答题
19.已知一次函数y=2ax+4a﹣6,当﹣1≤x≤1时函数值都y都大于0,求a的取值范围.
20.关于x的函数y=(m+1)x|m|+3﹣n.
(1)m,n取何值时,函数是关于x的一次函数;
(2)m,n取何值时,函数是关于x的正比例函数.
21.已知一次函数y=2x﹣3.
(1)当x=﹣2时,求y.
(2)当y=1时,求x.
(3)当﹣3<y<0时,求x的取值范围.
22.已知y是x的一次函数,且当x=1时,y=﹣2;当x=2时,y=1.
(1)求这个一次函数的表达式;
(2)通过计算,判断点P(4,6)是否在这个函数的图象上?
23.如图是函数y=﹣x+5的一部分图象,利用图象回答下列问题:
①自变量x的取值范围是什么?
②在x的取值范围内,y随x的增大而怎样变化?
③当x取什么值时,y取到最小值,最小值是多少?
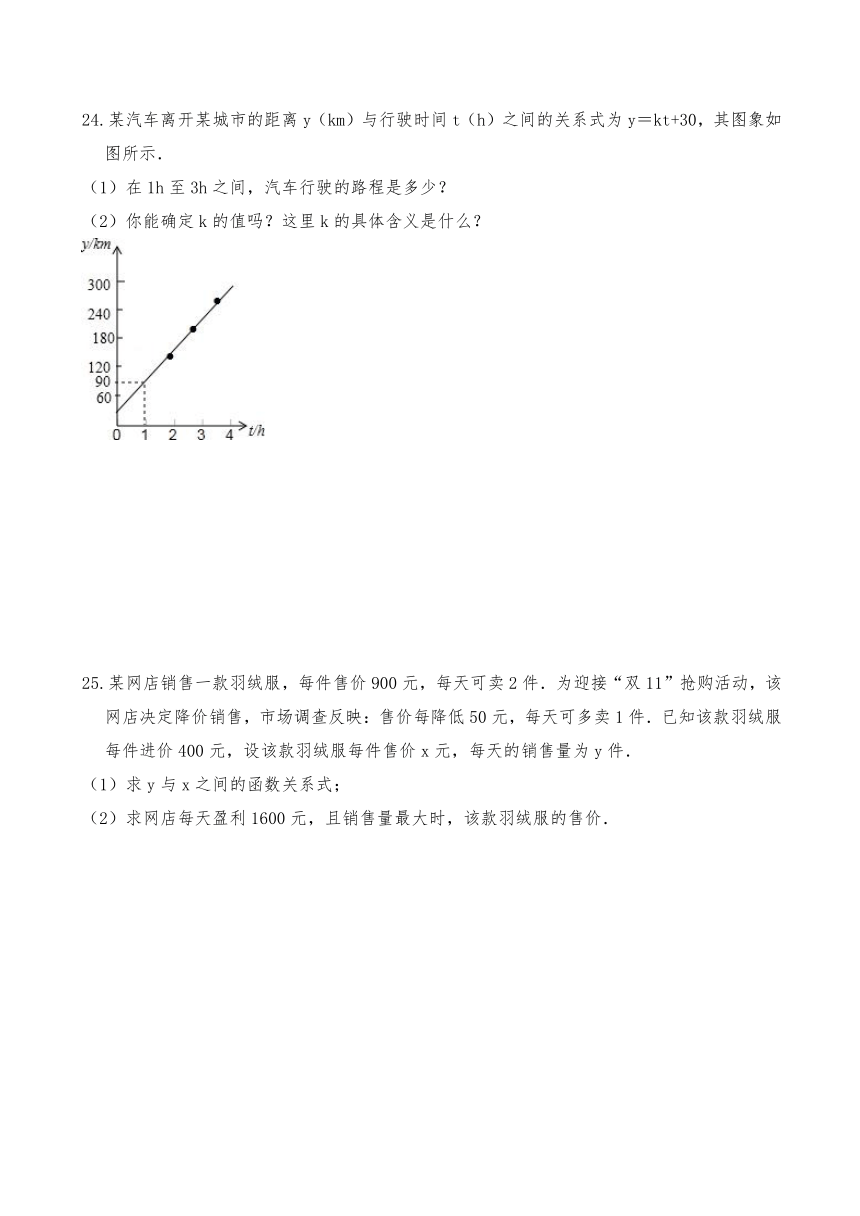
24.某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示.
(1)在1h至3h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
25.某网店销售一款羽绒服,每件售价900元,每天可卖2件.为迎接“双11”抢购活动,该网店决定降价销售,市场调查反映:售价每降低50元,每天可多卖1件.已知该款羽绒服每件进价400元,设该款羽绒服每件售价x元,每天的销售量为y件.
(1)求y与x之间的函数关系式;
(2)求网店每天盈利1600元,且销售量最大时,该款羽绒服的售价.
答案
一、单选题
1.B
【分析】根据一次函数的定义条件进行逐一分析即可.
【解答】解:①y=x﹣6符合一次函数的定义,故本选项正确;
②y=是反比例函数;故本选项错误;
③y=,属于正比例函数,是一次函数的特殊形式,故本选项正确;
④y=7﹣x符合一次函数的定义,故本选项正确;
综上所述,符合题意的是①③④;
故选:B.
2.A
【分析】由k=2>0,利用一次函数的性质可得出y随x的增大而增大,结合﹣2<1,即可得出m<n.
【解答】解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<1,
∴m<n.
故选:A.
3.C
【分析】由k=4>0,利用一次函数的性质可得出y随x的增大而增大,再结合x1<x2,即可得出y1<y2.
【解答】解:∵k=4>0,
∴y随x的增大而增大,
又∵x1<x2,
∴y1<y2.
故选:C.
4.D
【分析】根据一次函数的定义得出|m|=1,求出即可.
【解答】解:∵y=2x|m|+3表示一次函数,
∴|m|=1,
解得:m=±1,
故选:D.
5.C
【分析】直线y=kx+b(k≠0)与y轴交于点(0,b),依据直线y=kx+b(k≠0)经过点A(2,﹣3),即可得出b=﹣3﹣2k,再根据直线y=kx+b(k≠0)与y轴的交点在x轴上方,即可得到k的取值范围.
【解答】解:直线y=kx+b(k≠0)中,令x=0,则y=b,
∴直线y=kx+b(k≠0)与y轴交于点(0,b),
又∵直线y=kx+b(k≠0)经过点A(2,﹣3),
∴﹣3=2k+b,
∴b=﹣3﹣2k,
又∵直线y=kx+b(k≠0)与y轴的交点在x轴上方,
∴b>0,即﹣3﹣2k>0,
解得k<,
故选:C.
6.D
【分析】根据题意和函数图象中的数据可以判断各个选项中的结论是否正确,从而可以解答本题.
【解答】解;由图可得,
乙比甲提前:40﹣28=12分钟到达,故①错误,
甲的平均速度为:10÷=15千米/小时,故②正确,
乙的速度为:10÷=60千米/小时,
设甲、乙相遇时,甲走了x分钟,
15×=60×,
解得,x=24,
则甲、乙相遇时,乙走了=6千米,故③正确,
乙出发24﹣18=6分钟追上甲,故④正确,
故选:D.
二、填空题
7.3
【分析】根据一次函数y=kx+b的定义条件:k、b为常数,k≠0,自变量次数为1解答即可.
【解答】解:∵函数y=(n+3)x|n|﹣2是一次函数,
∴|n|﹣2=1,n+3≠0,
∴n=±3,n≠﹣3,
∴n=3,
故答案为:n=3.
8.(1)(2)(4)
【分析】根据一次函数的定义对各小题进行逐一分析即可.
【解答】解:(1)y=3πx是正比例函数也是一次函数;(2)y=8x﹣6是一次函数;(3)y=是反比例函数;(4)y=﹣8x式一次函数;(5)y=5x2﹣4x+1是二次函数,
故答案为:(1)(2)(4).
9.y=2x+1
【分析】根据函数的平移规律,可得答案.
【解答】解:将直线y=2x+4向下平移3个单位,得
y=2x+4﹣3,
化简,得
y=2x+1,
故答案为:y=2x+1.
10.-1
【分析】由正比例函数图象过点A,可知点A的坐标满足正比例函数的关系式,由此可得出关于a的一元一次方程,解方程即可得出结论.
【解答】解:∵正比例函数y=﹣2x的图象经过点A(a﹣1,4),
∴4=﹣2(a﹣1),解得:a=﹣1.
故答案为:﹣1.
11.y=2x+3
【分析】直接利用一次函数的平移规律进而得出答案.
【解答】解:把直线y=2x﹣1向左平移1个单位长度,得到y=2(x+1)﹣1=2x+1,
再向上平移2个单位长度,得到y=2x+3.
故答案为:y=2x+3.
12.-12 4
【分析】根据当x=﹣2时,当y=6时,分别代入函数解析式求出即可.
【解答】解:∵对于函数y=3x﹣6,∴当x=﹣2时,y=3×(﹣2)﹣6=﹣12,
当y=6时,6=3x﹣6,解得x=4.
故答案为:﹣12,4.
13.①②⑥ ⑥
【分析】用x表示成y的函数后,若符合y=kx+b(k≠0)的形式,是一次函数,若符合y=kx(k≠0)的形式,是正比例函数.
【解答】解:①是一次函数;
②可整理为y=﹣x+1的形式,是一次函数;
③y=,是反比例函数;
④不属于所学的函数;
⑤是二次函数;
⑥是一次函数,也是正比例函数,
∴属于一次函数的有①②⑥,属正比例函数的有⑥,
故答案为①②⑥;⑥.
14.x=-3
【分析】令一次函数的y值为﹣1,此时一次函数可转化为所求的方程;因此与函数值为﹣1所对应的x值即为所求方程的解.
【解答】解:由题意可知,当x=﹣3时,函数值为﹣1;
因此当x=﹣3时,ax+b=﹣1,
即方程ax+b=﹣1的解为:x=﹣3.
故答案是:x=﹣3.
15.2<x<3
【分析】0<mx+n<﹣x+a表示在x轴的上方,且y2=﹣x+a的图象在y1=mx+n的图象的上边部分自变量的取值范围,依据函数图象中两直线的位置,即可得到不等式组0<mx+n<﹣x+a的解集为2<x<3.
【解答】解:由图可得,当0<mx+n时,x>2;
当mx+n<﹣x+a时,x<3;
∴不等式组0<mx+n<﹣x+a的解集为2<x<3,
故答案为:2<x<3.
16.y=3x-1
【分析】根据平移不改变k的值可设平移后直线的解析式为y=3x+b,然后将点(0,﹣1)代入即可得出直线的函数解析式.
【解答】解:设平移后直线的解析式为y=3x+b,
把(0,﹣1)代入直线解析式得﹣1=b,
解得 b=﹣1.
所以平移后直线的解析式为y=3x﹣1.
故答案为:y=3x﹣1.
17.4
【分析】根据图中信息找出甲,乙两人行驶的路程和时间,进而求出速度即可.
【解答】解:根据图象可得:
∵甲行驶距离为100千米时,行驶时间为5小时,乙行驶距离为80千米时,行驶时间为5小时,
∴甲的速度是:100÷5=20(千米/时);乙的速度是:80÷5=16(千米/时);
故这两人骑自行车的速度相差:20﹣16=4(千米/时);
解法二:利用待定系数法s=k甲t+b,s=k乙t,
易得得k甲=16,k乙=20,
∵速度=路程÷时间
所以k甲、k乙分别为甲、乙的速度
故速度差为20﹣16=4km/h
故答案为:4.
18.150
【分析】这是一个一次函数模型,设y=kx+b,利用待定系数法即可解决问题,
【解答】解:这是一个一次函数模型,设y=kx+b,则有,
解得,
∴y=5x+115,
当x=7时,y=150,
∴预测今年6月7日该商店销售纯净水的数量约为150瓶,
故答案为150.
三、解答题
19.解:当a=0时,y=﹣6,﹣6<0,
∴a≠0.
根据题意得:,
解得:a>3.
∴a的取值范围为a>3.
20.解:(1)由题意,得
|m|=1,且m+1≠0,3﹣n为任意值
解得m=1;n为任意实数.
(2)由题意,得
|m|=1,且m+1≠0,3﹣n=0,
解得m=1,n=3.
21.解:(1)把x=﹣2代入y=2x﹣3中得:y=﹣4﹣3=﹣7;
(2)把y=1代入y=2x﹣3中得:1=2x﹣3,
解得:x=2;
(3)∵﹣3<y<0,
∴﹣3<2x﹣3<0,
∴,
解得:0<x<.
22.解:(1)设一次函数解析式为y=kx+b,
根据题意得,解得,
∴这个一次函数的表达式为y=3x﹣5;
(2)∵当x=4时,y=3x﹣5=3×4﹣5=7≠6,
∴点P(4,6)不在这个函数的图象上.
23.解:
(1)由图象可知当图象在AB之间时,对应的x的范围为0<x≤5,
即自变量x的取值范围为0<x≤5;
(2)由图象可知图象呈下降趋势,
∴y随x的增大而减小;
(3)由(2)可知函数y随x的增大而减小,
∴当x=5时y有最小值,结合图象可知y的最小值为2.5.
24.解:根据函数图象可知:t=1时,y=90.
将t=1,y=90代入得:k+30=90.
解得;k=60.
所以函数的关系式为y=60t+30.
将t=3代入得:y=210.
∴在1h至3h之间,汽车行驶的路程=210﹣90=120km;
(2)由(1)可知:k=60,k的具体含义是汽车的行驶速度.
25.解:(1)依题意,得:y=2+=20﹣.
(2)依题意,得:(x﹣400)(20﹣)=1600,
解得:x1=600,x2=800,
∵销售量最大,
∴x=600.
答:当每件售价定为600元时,该网店每天盈利1600元.
一、单选题
1.下列函数中,y是x的一次函数的是( )
①y=x﹣6;②y=;③y=;④y=7﹣x.
A.①②③ B.①③④ C.①②③④ D.②③④
2.若直线y=2x+b经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的是( )
A.m<n B.m>n C.m=n D.无法确定
3.点P1(x1,y1),点P2(x2,y2)是一次函数y=4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
4.y=2x|m|+3表示一次函数,则m等于( )
A.1 B.﹣1 C.0或﹣1 D.1或﹣1
5.若直线y=kx+b(k≠0)经过点A(2,﹣3),且与y轴的交点在x轴上方,则k的取值范围是( )
A.k> B.k>﹣ C.k<﹣ D.k<
6.如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法:
①甲比乙提前12分钟到达;
②甲的平均速度为15千米/小时;
③甲、乙相遇时,乙走了6千米;
④乙出发6分钟后追上甲,其中正确的是( )
A.①② B.③④ C.①③④ D.②③④
二、填空题
7.已知函数y=(n+3)x|n|﹣2是一次函数,则n= .
8.下列函数(1)y=3πx;(2)y=8x﹣6;(3)y=;(4)y=﹣8x;(5)y=5x2﹣4x+1中,是一次函数的有 .
9.将直线y=2x+4向下平移3个单位,则得到的新直线的解析式为 .
10.若正比例函数y=﹣2x的图象经过点A(a﹣1,4),则a的值是 ﹣ .
11.把直线y=2x﹣1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为 .
12.对于函数y=3x﹣6,当x=﹣2时,y= ﹣ ,当y=6时,x= .
13.函数:①y=﹣2x+3;②x+y=1;③xy=1;④y=;⑤y=+1;⑥y=0.5x中,属于一次函数的有 ,属正比例函数的有 (只填序号)
14.若一次函数y=ax+b(a≠0)的图象经过(3,2)和(﹣3,﹣1)两点,则方程ax+b=﹣1的解为 .
15.一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则0<mx+n<﹣x+a的解集为 .
16.如果将直线y=3x平移,使其经过点(0,﹣1),那么平移后的直线表达式是 ﹣ .
17.如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
18.某商店今年6月初销售纯净水的数量如下表所示:
日期 1 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
三、解答题
19.已知一次函数y=2ax+4a﹣6,当﹣1≤x≤1时函数值都y都大于0,求a的取值范围.
20.关于x的函数y=(m+1)x|m|+3﹣n.
(1)m,n取何值时,函数是关于x的一次函数;
(2)m,n取何值时,函数是关于x的正比例函数.
21.已知一次函数y=2x﹣3.
(1)当x=﹣2时,求y.
(2)当y=1时,求x.
(3)当﹣3<y<0时,求x的取值范围.
22.已知y是x的一次函数,且当x=1时,y=﹣2;当x=2时,y=1.
(1)求这个一次函数的表达式;
(2)通过计算,判断点P(4,6)是否在这个函数的图象上?
23.如图是函数y=﹣x+5的一部分图象,利用图象回答下列问题:
①自变量x的取值范围是什么?
②在x的取值范围内,y随x的增大而怎样变化?
③当x取什么值时,y取到最小值,最小值是多少?
24.某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示.
(1)在1h至3h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
25.某网店销售一款羽绒服,每件售价900元,每天可卖2件.为迎接“双11”抢购活动,该网店决定降价销售,市场调查反映:售价每降低50元,每天可多卖1件.已知该款羽绒服每件进价400元,设该款羽绒服每件售价x元,每天的销售量为y件.
(1)求y与x之间的函数关系式;
(2)求网店每天盈利1600元,且销售量最大时,该款羽绒服的售价.
答案
一、单选题
1.B
【分析】根据一次函数的定义条件进行逐一分析即可.
【解答】解:①y=x﹣6符合一次函数的定义,故本选项正确;
②y=是反比例函数;故本选项错误;
③y=,属于正比例函数,是一次函数的特殊形式,故本选项正确;
④y=7﹣x符合一次函数的定义,故本选项正确;
综上所述,符合题意的是①③④;
故选:B.
2.A
【分析】由k=2>0,利用一次函数的性质可得出y随x的增大而增大,结合﹣2<1,即可得出m<n.
【解答】解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<1,
∴m<n.
故选:A.
3.C
【分析】由k=4>0,利用一次函数的性质可得出y随x的增大而增大,再结合x1<x2,即可得出y1<y2.
【解答】解:∵k=4>0,
∴y随x的增大而增大,
又∵x1<x2,
∴y1<y2.
故选:C.
4.D
【分析】根据一次函数的定义得出|m|=1,求出即可.
【解答】解:∵y=2x|m|+3表示一次函数,
∴|m|=1,
解得:m=±1,
故选:D.
5.C
【分析】直线y=kx+b(k≠0)与y轴交于点(0,b),依据直线y=kx+b(k≠0)经过点A(2,﹣3),即可得出b=﹣3﹣2k,再根据直线y=kx+b(k≠0)与y轴的交点在x轴上方,即可得到k的取值范围.
【解答】解:直线y=kx+b(k≠0)中,令x=0,则y=b,
∴直线y=kx+b(k≠0)与y轴交于点(0,b),
又∵直线y=kx+b(k≠0)经过点A(2,﹣3),
∴﹣3=2k+b,
∴b=﹣3﹣2k,
又∵直线y=kx+b(k≠0)与y轴的交点在x轴上方,
∴b>0,即﹣3﹣2k>0,
解得k<,
故选:C.
6.D
【分析】根据题意和函数图象中的数据可以判断各个选项中的结论是否正确,从而可以解答本题.
【解答】解;由图可得,
乙比甲提前:40﹣28=12分钟到达,故①错误,
甲的平均速度为:10÷=15千米/小时,故②正确,
乙的速度为:10÷=60千米/小时,
设甲、乙相遇时,甲走了x分钟,
15×=60×,
解得,x=24,
则甲、乙相遇时,乙走了=6千米,故③正确,
乙出发24﹣18=6分钟追上甲,故④正确,
故选:D.
二、填空题
7.3
【分析】根据一次函数y=kx+b的定义条件:k、b为常数,k≠0,自变量次数为1解答即可.
【解答】解:∵函数y=(n+3)x|n|﹣2是一次函数,
∴|n|﹣2=1,n+3≠0,
∴n=±3,n≠﹣3,
∴n=3,
故答案为:n=3.
8.(1)(2)(4)
【分析】根据一次函数的定义对各小题进行逐一分析即可.
【解答】解:(1)y=3πx是正比例函数也是一次函数;(2)y=8x﹣6是一次函数;(3)y=是反比例函数;(4)y=﹣8x式一次函数;(5)y=5x2﹣4x+1是二次函数,
故答案为:(1)(2)(4).
9.y=2x+1
【分析】根据函数的平移规律,可得答案.
【解答】解:将直线y=2x+4向下平移3个单位,得
y=2x+4﹣3,
化简,得
y=2x+1,
故答案为:y=2x+1.
10.-1
【分析】由正比例函数图象过点A,可知点A的坐标满足正比例函数的关系式,由此可得出关于a的一元一次方程,解方程即可得出结论.
【解答】解:∵正比例函数y=﹣2x的图象经过点A(a﹣1,4),
∴4=﹣2(a﹣1),解得:a=﹣1.
故答案为:﹣1.
11.y=2x+3
【分析】直接利用一次函数的平移规律进而得出答案.
【解答】解:把直线y=2x﹣1向左平移1个单位长度,得到y=2(x+1)﹣1=2x+1,
再向上平移2个单位长度,得到y=2x+3.
故答案为:y=2x+3.
12.-12 4
【分析】根据当x=﹣2时,当y=6时,分别代入函数解析式求出即可.
【解答】解:∵对于函数y=3x﹣6,∴当x=﹣2时,y=3×(﹣2)﹣6=﹣12,
当y=6时,6=3x﹣6,解得x=4.
故答案为:﹣12,4.
13.①②⑥ ⑥
【分析】用x表示成y的函数后,若符合y=kx+b(k≠0)的形式,是一次函数,若符合y=kx(k≠0)的形式,是正比例函数.
【解答】解:①是一次函数;
②可整理为y=﹣x+1的形式,是一次函数;
③y=,是反比例函数;
④不属于所学的函数;
⑤是二次函数;
⑥是一次函数,也是正比例函数,
∴属于一次函数的有①②⑥,属正比例函数的有⑥,
故答案为①②⑥;⑥.
14.x=-3
【分析】令一次函数的y值为﹣1,此时一次函数可转化为所求的方程;因此与函数值为﹣1所对应的x值即为所求方程的解.
【解答】解:由题意可知,当x=﹣3时,函数值为﹣1;
因此当x=﹣3时,ax+b=﹣1,
即方程ax+b=﹣1的解为:x=﹣3.
故答案是:x=﹣3.
15.2<x<3
【分析】0<mx+n<﹣x+a表示在x轴的上方,且y2=﹣x+a的图象在y1=mx+n的图象的上边部分自变量的取值范围,依据函数图象中两直线的位置,即可得到不等式组0<mx+n<﹣x+a的解集为2<x<3.
【解答】解:由图可得,当0<mx+n时,x>2;
当mx+n<﹣x+a时,x<3;
∴不等式组0<mx+n<﹣x+a的解集为2<x<3,
故答案为:2<x<3.
16.y=3x-1
【分析】根据平移不改变k的值可设平移后直线的解析式为y=3x+b,然后将点(0,﹣1)代入即可得出直线的函数解析式.
【解答】解:设平移后直线的解析式为y=3x+b,
把(0,﹣1)代入直线解析式得﹣1=b,
解得 b=﹣1.
所以平移后直线的解析式为y=3x﹣1.
故答案为:y=3x﹣1.
17.4
【分析】根据图中信息找出甲,乙两人行驶的路程和时间,进而求出速度即可.
【解答】解:根据图象可得:
∵甲行驶距离为100千米时,行驶时间为5小时,乙行驶距离为80千米时,行驶时间为5小时,
∴甲的速度是:100÷5=20(千米/时);乙的速度是:80÷5=16(千米/时);
故这两人骑自行车的速度相差:20﹣16=4(千米/时);
解法二:利用待定系数法s=k甲t+b,s=k乙t,
易得得k甲=16,k乙=20,
∵速度=路程÷时间
所以k甲、k乙分别为甲、乙的速度
故速度差为20﹣16=4km/h
故答案为:4.
18.150
【分析】这是一个一次函数模型,设y=kx+b,利用待定系数法即可解决问题,
【解答】解:这是一个一次函数模型,设y=kx+b,则有,
解得,
∴y=5x+115,
当x=7时,y=150,
∴预测今年6月7日该商店销售纯净水的数量约为150瓶,
故答案为150.
三、解答题
19.解:当a=0时,y=﹣6,﹣6<0,
∴a≠0.
根据题意得:,
解得:a>3.
∴a的取值范围为a>3.
20.解:(1)由题意,得
|m|=1,且m+1≠0,3﹣n为任意值
解得m=1;n为任意实数.
(2)由题意,得
|m|=1,且m+1≠0,3﹣n=0,
解得m=1,n=3.
21.解:(1)把x=﹣2代入y=2x﹣3中得:y=﹣4﹣3=﹣7;
(2)把y=1代入y=2x﹣3中得:1=2x﹣3,
解得:x=2;
(3)∵﹣3<y<0,
∴﹣3<2x﹣3<0,
∴,
解得:0<x<.
22.解:(1)设一次函数解析式为y=kx+b,
根据题意得,解得,
∴这个一次函数的表达式为y=3x﹣5;
(2)∵当x=4时,y=3x﹣5=3×4﹣5=7≠6,
∴点P(4,6)不在这个函数的图象上.
23.解:
(1)由图象可知当图象在AB之间时,对应的x的范围为0<x≤5,
即自变量x的取值范围为0<x≤5;
(2)由图象可知图象呈下降趋势,
∴y随x的增大而减小;
(3)由(2)可知函数y随x的增大而减小,
∴当x=5时y有最小值,结合图象可知y的最小值为2.5.
24.解:根据函数图象可知:t=1时,y=90.
将t=1,y=90代入得:k+30=90.
解得;k=60.
所以函数的关系式为y=60t+30.
将t=3代入得:y=210.
∴在1h至3h之间,汽车行驶的路程=210﹣90=120km;
(2)由(1)可知:k=60,k的具体含义是汽车的行驶速度.
25.解:(1)依题意,得:y=2+=20﹣.
(2)依题意,得:(x﹣400)(20﹣)=1600,
解得:x1=600,x2=800,
∵销售量最大,
∴x=600.
答:当每件售价定为600元时,该网店每天盈利1600元.
