2023-2024学年福建省莆田四中高一(下)第一次月考数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年福建省莆田四中高一(下)第一次月考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 09:15:37 | ||
图片预览




文档简介
2023-2024学年福建省莆田四中高一(下)第一次月考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,,则( )
A. B. C. D.
2.已知复数是纯虚数,则实数( )
A. B. C. D.
3.已知平面向量,满足,,且,则与的夹角是( )
A. B. C. D.
4.在中,若,,,则( )
A. B. C. D.
5.在直角坐标系中,已知,,若,恒成立,则( )
A. B. C. D.
6.在中,角,,所对的边分别是,,,,,则是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形
7.如图,已知正方形的边长为,若动点在以为直径的半圆上正方形内部,含边界,则的取值范围为( )
A.
B.
C.
D.
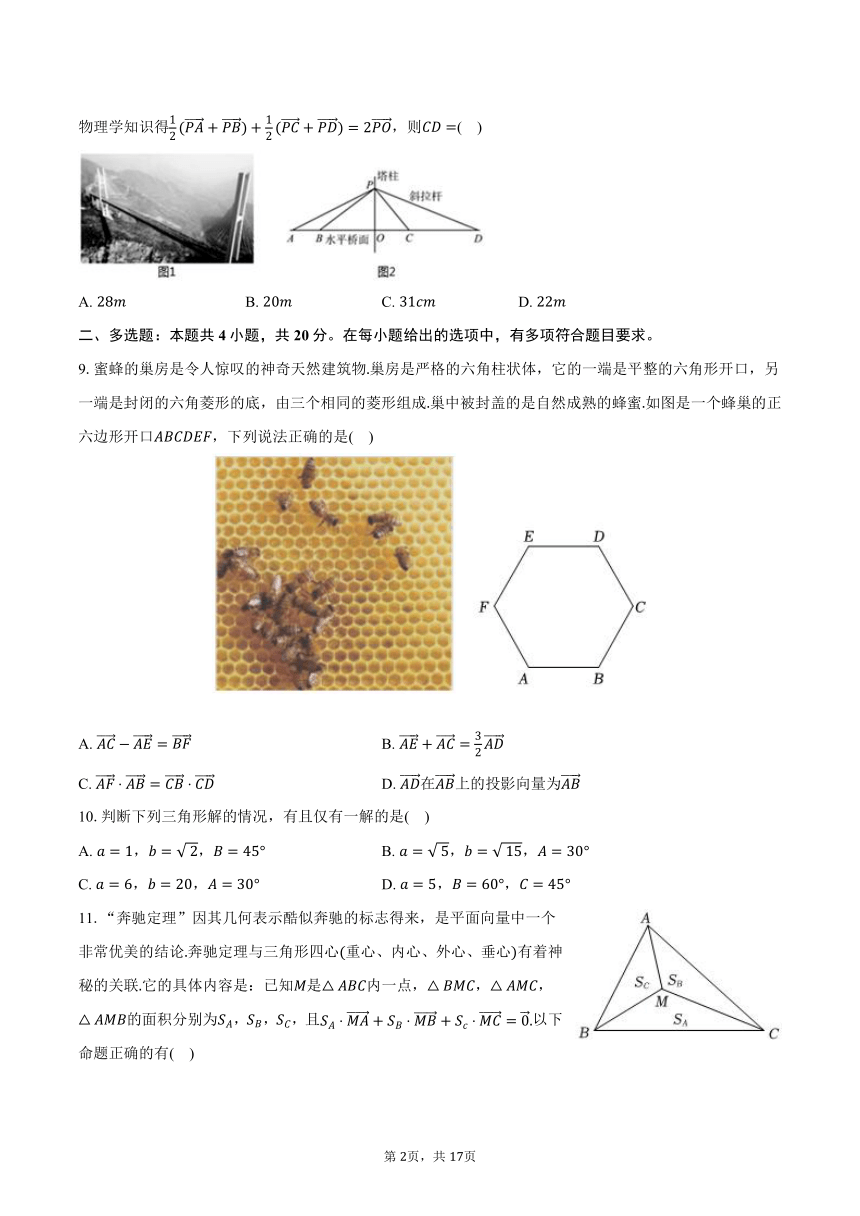
8.图是世界最高桥贵州北盘江斜拉桥.图是根据下左图作的简易侧视图为便于计算,侧视图与实物有区别在侧视图中,斜拉杆,,,的一端在垂直于水平面的塔柱上,另一端,,,与塔柱上的点都在桥面同一侧的水平直线上.已知,,,根据物理学知识得,则( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.蜜蜂的巢房是令人惊叹的神奇天然建筑物巢房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱形的底,由三个相同的菱形组成巢中被封盖的是自然成熟的蜂蜜如图是一个蜂巢的正六边形开口,下列说法正确的是( )
A. B.
C. D. 在上的投影向量为
10.判断下列三角形解的情况,有且仅有一解的是( )
A. ,, B. ,,
C. ,, D. ,,
11.“奔驰定理”因其几何表示酷似奔驰的标志得来,是平面向量中一个非常优美的结论奔驰定理与三角形四心重心、内心、外心、垂心有着神秘的关联它的具体内容是:已知是内一点,,,的面积分别为,,,且以下命题正确的有( )
A. 若::::,则为的重心
B. 若为的内心,则
C. 若,,为的外心,则
D. 若为的垂心,,则
12.已知扇形的半径为,,点在弧上运动,,下列说法正确的有( )
A. 当位于点时,的值最小 B. 当位于点时,的值最大
C. 的取值范围为 D. 的取值范围
三、填空题:本题共4小题,每小题5分,共20分。
13.已知向量,,若,则 ______.
14.在中,若,,,则的最大角与最小角之和是______.
15.在中,若为,的交点,满足,则的值为______.
16.在中,,点与点分别在直线的两侧,且,,则的长度的最大值是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知复数,其中为虚数单位,.
若为实数,求的值;
若复数在复平面内对应的点在直线上,求的值.
18.本小题分
设是不共线的两个非零向量。
若,求证:三点共线;
若与共线,求实数的值;
19.本小题分
中,角,,所对的边分别为,,,,,.
,时,求的长度;
若为角的平分线,且,求的面积.
20.本小题分
已知向量,函数.
求函数的最大值及相应自变量的取值;
在中,角,,的对边分别为,,,若,求的取值范围.
21.本小题分
已知某商场门前是一块角形区域,如图所示,其中,且在该区域内点处有一个路灯,经测量点到区域边界、的距离分别为,,为长度单位现准备过点修建一条长椅点,分别落在、上,长椅的宽度及路灯的粗细忽略不计,以供购买冷饮的人休息.
求点到点的距离;
为优化商场的经营面积,当等于多少时,该三角形区域面积最小?并求出面积的最小值.
22.本小题分
在中,,,对应的边分别为,,,.
求;
奥古斯丁路易斯柯西年年,法国著名数学家柯西在数学领域有非常高的造诣很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用现在,在的条件下,若,是内一点,过作,,垂线,垂足分别为,,,借助于三维分式型柯西不等式:当且仅当时等号成立求的最小值.
答案和解析
1.【答案】
【解析】解:由已知条件可得,,
因此,.
故选:.
利用向量的数量积的运算法则,求解即可.
本题考查向量的数量积的求法,是基础题.
2.【答案】
【解析】解:是纯虚数,
,解得.
故选:.
把复数化为的形式,再由实部为且虚部不为列式求得值.
本题考查复数代数形式的基本运算,考查复数的基本概念,是基础题.
3.【答案】
【解析】即:设与的夹角为,则
又因为,
所以.
故选:.
利用向量的夹角公式即可求解.
本题主要考查向量的夹角公式,属于基础题.
4.【答案】
【解析】解:,,
则,
,,
由正弦定理可知,.
故选:.
根据已知条件,结合正弦定理,即可求解.
本题主要考查正弦定理的应用,属于基础题.
5.【答案】
【解析】解:由题意得,,,
若,恒成立,
则,恒成立,
即,恒成立,
恒成立,
又,当时等号成立,
故,即,
.
故选:.
题意转化为恒成立,结合二次函数的最值,可得,即可得出答案.
本题考查平面向量的线性运算,考查转化思想,考查逻辑推理能力和运算能力,属于中档题.
6.【答案】
【解析】解:由边化角可得,
因为,
所以,即,
所以,
因为,所以,所以,
所以解得,所以,
所以是直角三角形.
故选:.
利用正弦定理和三角恒等变换公式可求出即可判断求解.
本题主要考查正弦定理和三角恒等变换公式,属于基础题.
7.【答案】
【解析】解:建立直角坐标系,如图所示:正方形的边长为,
设:,,,,
取的中点,连接,所以的取值范围为,
即,
由于,
故.
故选:.
直接利用向量的数量积运算求出结果.
本题考查的知识要点:向量的数量积运算,主要考查学生的理解能力和计算能力,属于中档题.
8.【答案】
【解析】解:,
,
又,于是,
,,
,
设线段中点为,线段中点为,
,
,
为线段中点,
,
,即,
.
故选:.
易知,结合,可知,进而求得,设线段中点为,线段中点为,结合题意可得为线段中点,从而容易得到答案.
本题主要考查平面向量的综合运用,考查转化思想及运算求解能力,属于中档题.
9.【答案】
【解析】解:建立如图所示的平面直角坐标系,
不妨设,
则,,,,,,
对于选项A,,,即,即选项A错误;
对于选项B,,,即,即选项B正确;
对于选项C,,,即,即选项C正确;
对于选项D,在上的投影向量为,即选项D正确.
故选:.
先建立平面直角坐标系,求出对应点的坐标,然后结合平面向量数量积的运算求解即可.
本题考查了平面向量数量积的运算,重点考查了平面向量数量积的坐标运算,属中档题.
10.【答案】
【解析】解:对于:由正弦定理得,,,即,,则三角形有唯一解,故A正确;
对于:由正弦定理得,,,即,或,则三角形有两解,故B错误;
对于:由正弦定理得,此时无解,故C错误;
对于:三角形两角和一边确定时,三角形有唯一确定解,D正确.
故选:.
利用正弦定理解三角形,即可得出答案.
本题考查解三角形,考查转化思想,考查运算能力,属于基础题.
11.【答案】
【解析】解:对于,取的中点,连接,,
由::::,则,
所以,
所以,,三点共线,且,
设,分别为,的中点,同理可得,,
所以为的重心,故A正确;
对于,由为的内心,则可设内切圆半径为,
则有,,,
所以,
即,故B正确;
对于,由为的外心,则可设的外接圆半径为,
因为,,
则有,,,
所以,,,
所以,故C错误;
对于,如图,延长交于点,延长交于点,延长交于点,
由为的垂心,,则::::,
又,则,,
设,,则,,
所以,即,
所以,所以,故D正确;
故选:.
对,取的中点,连接,,结合奔驰定理可得到,进而即可判断;对,设内切圆半径为,从而可用表示出,,,再结合奔驰定理即可判断;对,设的外接圆半径为,根据圆的性质结合题意可得,,,从而可用表示出,,,进而即可判断;对,延长交于点,延长交于点,延长交于点,根据题意结合奔驰定理可得到,,从而可设,,则,,代入即可求解,进而即可判断.
本题主要考查了平面向量的数量积运算,考查了三角形的重心、内心、外心和垂心的性质,属于中档题.
12.【答案】
【解析】解:以为原点,以所在直线为轴,过作的垂线为轴,建立平面直角坐标系,
设,则,其中,,,
,
,即,
,
当时,取得最大值,此时点为或点,故A正确,B错误;
而,,
,
,,,
,
的取值范围为,故C正确;
,
,,,
,
,故D正确.
故选:.
建立坐标系,得出点的坐标,进而可得向量的坐标,转化已知问题为三角函数的最值可判断结合选项逐一求解.
本题考查平面向量运算法则、向量数量积公式、三角函数的性质等基础知识,考查运算求解能力,是中档题.
13.【答案】
【解析】解:向量,,若,
则
解得.
故答案为:.
直接利用向量的数量积运算法则求解即可.
本题考查斜率的数量积的运算,向量创造条件的应用,是基础题.
14.【答案】
【解析】解:根据三角形中大角对大边,小角对小边的原则,
所以由余弦定理可知,
所以所对的角为.
所以三角形的最大角与最小角之和为:.
故答案为:.
直接利用余弦定理求出所对的角的余弦值,求出角的大小,利用三角形的内角和,求解最大角与最小角之和.
本题考查余弦定理的应用,三角形的边角对应关系的应用,考查计算能力.
15.【答案】
【解析】解:依题意,得,,三点共线,
所以,
同理:由,,三点共线,可得,
所以,解得,
所以,
又,所以,,
故.
故答案为:.
利用平面向量三点共线性质可得,,从而求得,进而得到,由此得解.
本题考查平面向量的线性运算,属中档题.
16.【答案】
【解析】解:在三角形中,设,则,且.
由正弦定理得,解得,
显然为锐角,故B.
.
设,.
在中,
.
又在中,.
代入式得:
.
令,则上式可化为,.
,令得,可见.
即,或舍
将代入式得,故因为开区间内唯一的极值点即为该函数的最值点
故答案为:.
根据可分析出是直角三角形,画出图形,可设,借助于余弦定理在三角形中表示出,然后再利用三角形借助于余弦定理找到与角的关系,代入表达式,利用导数研究函数最值的方法求解.
本题考查了利用正余弦定理解三角形的问题,同时也考查了导数在实际优化问题中的应用.还考查了学生的逻辑推理能力和数学运算能力.难度较大,
17.【答案】解:若为实数,
则有,得或.
若复数在复平面内对应的点在直线上,
则,得.
【解析】根据复数的概念列出方程,解方程即可求解;
根据复数的几何意义列出方程,解之即可求解.
本题主要考查实数的定义,以及复数的几何意义,属于基础题.
18.【答案】证明:,,,
,
,
、、三点共线;
解:与共线,存在实数,使得
,
与不共线,
,
,
.
【解析】本题考查了向量的运算和共线定理、向量基本定理,属于中档题.
利用向量的运算和共线定理即可得出;
利用向量共线定理和向量基本定理即可得出.
19.【答案】解:当时,,
则,
,
;
,即,
,
又,
,则,
.
【解析】根据题意,可得,然后根据向量的模长计算公式,即可得到结果;
根据题意,可得,然后结合三角形的面积公式即可得到,从而得到的面积.
本题主要考查解三角形,考查转化能力,属于中档题.
20.【答案】解:由题知,,
所以当,
即时,最大,且最大值为;
由知,,
则,
解得,或,
所以中,,又,
则,
整理得,
则,
当且仅当时,等号成立,
整理可得,
又在中,所以,
即的取值范围为.
【解析】利用向量坐标运算,二倍角公式和辅助角公式表示出,即可求出其最大值以及相应自变量的取值;
结合中的,求出,再利用余弦定理和基本不等式变形即可求出结果.
本题主要考查了向量的数量积运算,考查了余弦定理的应用,以及基本不等式的应用,属于中档题.
21.【答案】解:连接,在中,,,,
,由余弦定理得,
即,即点到点的距离为.
由,
,
,
平方得,
即,当且仅当,即时取等号,
,
故当时,三角形面积最小,最小值为.
【解析】在中,利用余弦定理进行计算即可.
根据三角形的面积公式以及基本不等式进行转化求解即可.
本题主要考查函数的应用问题,利用余弦定理,三角形的面积公式以及基本不等式进行转化求解是解决本题的关键,是中档题.
22.【答案】解:由正弦定理可得,
,,;
因为
,
当且仅当,即时等号成立,
由余弦定理,可知,
所以,所以,
所以,令,则,
,
又,当且仅当时取等号,
,,,所以,
令,
当时,取得最小值,此时取得最小值,
此时且.
【解析】本题考查正余弦定理的应用,考查运算求解能力,属较难题.
由正弦定理可得,可求;
利用三维分式型柯西不等式:,结合余弦定理及基本不等式与函数的单调性可求的最小值.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,,则( )
A. B. C. D.
2.已知复数是纯虚数,则实数( )
A. B. C. D.
3.已知平面向量,满足,,且,则与的夹角是( )
A. B. C. D.
4.在中,若,,,则( )
A. B. C. D.
5.在直角坐标系中,已知,,若,恒成立,则( )
A. B. C. D.
6.在中,角,,所对的边分别是,,,,,则是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形
7.如图,已知正方形的边长为,若动点在以为直径的半圆上正方形内部,含边界,则的取值范围为( )
A.
B.
C.
D.
8.图是世界最高桥贵州北盘江斜拉桥.图是根据下左图作的简易侧视图为便于计算,侧视图与实物有区别在侧视图中,斜拉杆,,,的一端在垂直于水平面的塔柱上,另一端,,,与塔柱上的点都在桥面同一侧的水平直线上.已知,,,根据物理学知识得,则( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.蜜蜂的巢房是令人惊叹的神奇天然建筑物巢房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱形的底,由三个相同的菱形组成巢中被封盖的是自然成熟的蜂蜜如图是一个蜂巢的正六边形开口,下列说法正确的是( )
A. B.
C. D. 在上的投影向量为
10.判断下列三角形解的情况,有且仅有一解的是( )
A. ,, B. ,,
C. ,, D. ,,
11.“奔驰定理”因其几何表示酷似奔驰的标志得来,是平面向量中一个非常优美的结论奔驰定理与三角形四心重心、内心、外心、垂心有着神秘的关联它的具体内容是:已知是内一点,,,的面积分别为,,,且以下命题正确的有( )
A. 若::::,则为的重心
B. 若为的内心,则
C. 若,,为的外心,则
D. 若为的垂心,,则
12.已知扇形的半径为,,点在弧上运动,,下列说法正确的有( )
A. 当位于点时,的值最小 B. 当位于点时,的值最大
C. 的取值范围为 D. 的取值范围
三、填空题:本题共4小题,每小题5分,共20分。
13.已知向量,,若,则 ______.
14.在中,若,,,则的最大角与最小角之和是______.
15.在中,若为,的交点,满足,则的值为______.
16.在中,,点与点分别在直线的两侧,且,,则的长度的最大值是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知复数,其中为虚数单位,.
若为实数,求的值;
若复数在复平面内对应的点在直线上,求的值.
18.本小题分
设是不共线的两个非零向量。
若,求证:三点共线;
若与共线,求实数的值;
19.本小题分
中,角,,所对的边分别为,,,,,.
,时,求的长度;
若为角的平分线,且,求的面积.
20.本小题分
已知向量,函数.
求函数的最大值及相应自变量的取值;
在中,角,,的对边分别为,,,若,求的取值范围.
21.本小题分
已知某商场门前是一块角形区域,如图所示,其中,且在该区域内点处有一个路灯,经测量点到区域边界、的距离分别为,,为长度单位现准备过点修建一条长椅点,分别落在、上,长椅的宽度及路灯的粗细忽略不计,以供购买冷饮的人休息.
求点到点的距离;
为优化商场的经营面积,当等于多少时,该三角形区域面积最小?并求出面积的最小值.
22.本小题分
在中,,,对应的边分别为,,,.
求;
奥古斯丁路易斯柯西年年,法国著名数学家柯西在数学领域有非常高的造诣很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用现在,在的条件下,若,是内一点,过作,,垂线,垂足分别为,,,借助于三维分式型柯西不等式:当且仅当时等号成立求的最小值.
答案和解析
1.【答案】
【解析】解:由已知条件可得,,
因此,.
故选:.
利用向量的数量积的运算法则,求解即可.
本题考查向量的数量积的求法,是基础题.
2.【答案】
【解析】解:是纯虚数,
,解得.
故选:.
把复数化为的形式,再由实部为且虚部不为列式求得值.
本题考查复数代数形式的基本运算,考查复数的基本概念,是基础题.
3.【答案】
【解析】即:设与的夹角为,则
又因为,
所以.
故选:.
利用向量的夹角公式即可求解.
本题主要考查向量的夹角公式,属于基础题.
4.【答案】
【解析】解:,,
则,
,,
由正弦定理可知,.
故选:.
根据已知条件,结合正弦定理,即可求解.
本题主要考查正弦定理的应用,属于基础题.
5.【答案】
【解析】解:由题意得,,,
若,恒成立,
则,恒成立,
即,恒成立,
恒成立,
又,当时等号成立,
故,即,
.
故选:.
题意转化为恒成立,结合二次函数的最值,可得,即可得出答案.
本题考查平面向量的线性运算,考查转化思想,考查逻辑推理能力和运算能力,属于中档题.
6.【答案】
【解析】解:由边化角可得,
因为,
所以,即,
所以,
因为,所以,所以,
所以解得,所以,
所以是直角三角形.
故选:.
利用正弦定理和三角恒等变换公式可求出即可判断求解.
本题主要考查正弦定理和三角恒等变换公式,属于基础题.
7.【答案】
【解析】解:建立直角坐标系,如图所示:正方形的边长为,
设:,,,,
取的中点,连接,所以的取值范围为,
即,
由于,
故.
故选:.
直接利用向量的数量积运算求出结果.
本题考查的知识要点:向量的数量积运算,主要考查学生的理解能力和计算能力,属于中档题.
8.【答案】
【解析】解:,
,
又,于是,
,,
,
设线段中点为,线段中点为,
,
,
为线段中点,
,
,即,
.
故选:.
易知,结合,可知,进而求得,设线段中点为,线段中点为,结合题意可得为线段中点,从而容易得到答案.
本题主要考查平面向量的综合运用,考查转化思想及运算求解能力,属于中档题.
9.【答案】
【解析】解:建立如图所示的平面直角坐标系,
不妨设,
则,,,,,,
对于选项A,,,即,即选项A错误;
对于选项B,,,即,即选项B正确;
对于选项C,,,即,即选项C正确;
对于选项D,在上的投影向量为,即选项D正确.
故选:.
先建立平面直角坐标系,求出对应点的坐标,然后结合平面向量数量积的运算求解即可.
本题考查了平面向量数量积的运算,重点考查了平面向量数量积的坐标运算,属中档题.
10.【答案】
【解析】解:对于:由正弦定理得,,,即,,则三角形有唯一解,故A正确;
对于:由正弦定理得,,,即,或,则三角形有两解,故B错误;
对于:由正弦定理得,此时无解,故C错误;
对于:三角形两角和一边确定时,三角形有唯一确定解,D正确.
故选:.
利用正弦定理解三角形,即可得出答案.
本题考查解三角形,考查转化思想,考查运算能力,属于基础题.
11.【答案】
【解析】解:对于,取的中点,连接,,
由::::,则,
所以,
所以,,三点共线,且,
设,分别为,的中点,同理可得,,
所以为的重心,故A正确;
对于,由为的内心,则可设内切圆半径为,
则有,,,
所以,
即,故B正确;
对于,由为的外心,则可设的外接圆半径为,
因为,,
则有,,,
所以,,,
所以,故C错误;
对于,如图,延长交于点,延长交于点,延长交于点,
由为的垂心,,则::::,
又,则,,
设,,则,,
所以,即,
所以,所以,故D正确;
故选:.
对,取的中点,连接,,结合奔驰定理可得到,进而即可判断;对,设内切圆半径为,从而可用表示出,,,再结合奔驰定理即可判断;对,设的外接圆半径为,根据圆的性质结合题意可得,,,从而可用表示出,,,进而即可判断;对,延长交于点,延长交于点,延长交于点,根据题意结合奔驰定理可得到,,从而可设,,则,,代入即可求解,进而即可判断.
本题主要考查了平面向量的数量积运算,考查了三角形的重心、内心、外心和垂心的性质,属于中档题.
12.【答案】
【解析】解:以为原点,以所在直线为轴,过作的垂线为轴,建立平面直角坐标系,
设,则,其中,,,
,
,即,
,
当时,取得最大值,此时点为或点,故A正确,B错误;
而,,
,
,,,
,
的取值范围为,故C正确;
,
,,,
,
,故D正确.
故选:.
建立坐标系,得出点的坐标,进而可得向量的坐标,转化已知问题为三角函数的最值可判断结合选项逐一求解.
本题考查平面向量运算法则、向量数量积公式、三角函数的性质等基础知识,考查运算求解能力,是中档题.
13.【答案】
【解析】解:向量,,若,
则
解得.
故答案为:.
直接利用向量的数量积运算法则求解即可.
本题考查斜率的数量积的运算,向量创造条件的应用,是基础题.
14.【答案】
【解析】解:根据三角形中大角对大边,小角对小边的原则,
所以由余弦定理可知,
所以所对的角为.
所以三角形的最大角与最小角之和为:.
故答案为:.
直接利用余弦定理求出所对的角的余弦值,求出角的大小,利用三角形的内角和,求解最大角与最小角之和.
本题考查余弦定理的应用,三角形的边角对应关系的应用,考查计算能力.
15.【答案】
【解析】解:依题意,得,,三点共线,
所以,
同理:由,,三点共线,可得,
所以,解得,
所以,
又,所以,,
故.
故答案为:.
利用平面向量三点共线性质可得,,从而求得,进而得到,由此得解.
本题考查平面向量的线性运算,属中档题.
16.【答案】
【解析】解:在三角形中,设,则,且.
由正弦定理得,解得,
显然为锐角,故B.
.
设,.
在中,
.
又在中,.
代入式得:
.
令,则上式可化为,.
,令得,可见.
即,或舍
将代入式得,故因为开区间内唯一的极值点即为该函数的最值点
故答案为:.
根据可分析出是直角三角形,画出图形,可设,借助于余弦定理在三角形中表示出,然后再利用三角形借助于余弦定理找到与角的关系,代入表达式,利用导数研究函数最值的方法求解.
本题考查了利用正余弦定理解三角形的问题,同时也考查了导数在实际优化问题中的应用.还考查了学生的逻辑推理能力和数学运算能力.难度较大,
17.【答案】解:若为实数,
则有,得或.
若复数在复平面内对应的点在直线上,
则,得.
【解析】根据复数的概念列出方程,解方程即可求解;
根据复数的几何意义列出方程,解之即可求解.
本题主要考查实数的定义,以及复数的几何意义,属于基础题.
18.【答案】证明:,,,
,
,
、、三点共线;
解:与共线,存在实数,使得
,
与不共线,
,
,
.
【解析】本题考查了向量的运算和共线定理、向量基本定理,属于中档题.
利用向量的运算和共线定理即可得出;
利用向量共线定理和向量基本定理即可得出.
19.【答案】解:当时,,
则,
,
;
,即,
,
又,
,则,
.
【解析】根据题意,可得,然后根据向量的模长计算公式,即可得到结果;
根据题意,可得,然后结合三角形的面积公式即可得到,从而得到的面积.
本题主要考查解三角形,考查转化能力,属于中档题.
20.【答案】解:由题知,,
所以当,
即时,最大,且最大值为;
由知,,
则,
解得,或,
所以中,,又,
则,
整理得,
则,
当且仅当时,等号成立,
整理可得,
又在中,所以,
即的取值范围为.
【解析】利用向量坐标运算,二倍角公式和辅助角公式表示出,即可求出其最大值以及相应自变量的取值;
结合中的,求出,再利用余弦定理和基本不等式变形即可求出结果.
本题主要考查了向量的数量积运算,考查了余弦定理的应用,以及基本不等式的应用,属于中档题.
21.【答案】解:连接,在中,,,,
,由余弦定理得,
即,即点到点的距离为.
由,
,
,
平方得,
即,当且仅当,即时取等号,
,
故当时,三角形面积最小,最小值为.
【解析】在中,利用余弦定理进行计算即可.
根据三角形的面积公式以及基本不等式进行转化求解即可.
本题主要考查函数的应用问题,利用余弦定理,三角形的面积公式以及基本不等式进行转化求解是解决本题的关键,是中档题.
22.【答案】解:由正弦定理可得,
,,;
因为
,
当且仅当,即时等号成立,
由余弦定理,可知,
所以,所以,
所以,令,则,
,
又,当且仅当时取等号,
,,,所以,
令,
当时,取得最小值,此时取得最小值,
此时且.
【解析】本题考查正余弦定理的应用,考查运算求解能力,属较难题.
由正弦定理可得,可求;
利用三维分式型柯西不等式:,结合余弦定理及基本不等式与函数的单调性可求的最小值.
第1页,共1页
同课章节目录
