物理鲁科版(2019)必修第二册4.1天地力的综合:万有引力定律 课件(共22张ppt)
文档属性
| 名称 | 物理鲁科版(2019)必修第二册4.1天地力的综合:万有引力定律 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-12 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第一节
万有引力定律
在浩瀚的宇宙中有无数大小不一、形态各异的天体,如月亮、地球、太阳、夜空中的星星。
人们对行星运动的认识过程是漫长复杂的,历史上有过不同的看法,科学家对此进行了不懈的探索,通过本节内容的学习,将使我们正确地认识行星的运动。
古人对地球的认识
古人根据有限范围内的观察(如日月星辰东升西落、远处天壤相接等),得出“天圆地方”之类的想法。
地心说与日心说
地
心
说
托 勒 密
日
心
说
哥白尼
第谷
开普勒
德国天文学家,第谷是他的
导师(1571—1630)在前人大量观测数据的基础上进一步完善了日心说。
行星三大定律
丹麦天文学家第谷(1546—1601),坚持对天体进行系统观测20余年,获得了大量精确资料
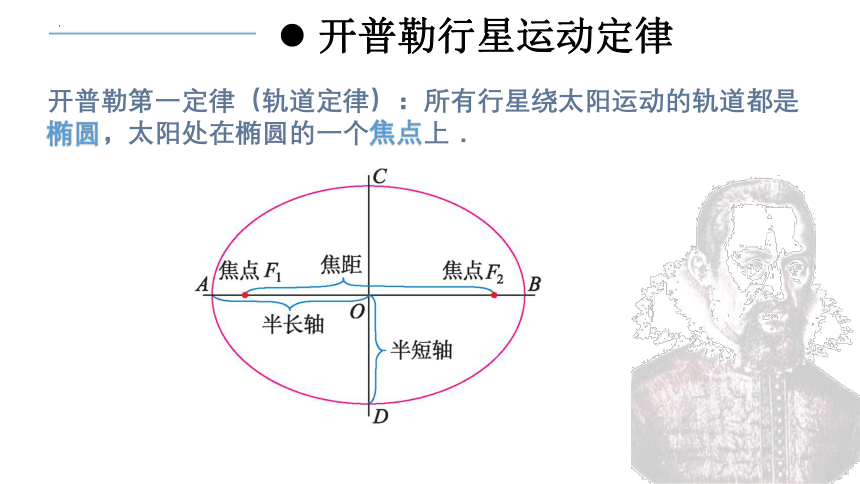
开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上.
开普勒行星运动定律
开普勒第二定律(面积定律):对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积.
远日点速度慢
近日点速度快
八大行星绕太阳运动的有关数据
a 是年的单位符号。
偏心率 e是椭圆扁平程度的量度,等于椭圆两焦点间的距离与长轴长度的比值。圆是椭圆的特例,偏心率为0。
开普勒第三定律(周期定律):所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.
表达式:
r3
T2
= k
半长轴
行星绕太阳公转的周期
k跟中心天体质量相关,与环绕天体无关
开普勒是用数学公式表达物理定律并最早获得成功的人之一。从此数学公式就成为表达物理学定律的基本方式。
温馨提示:
(1)开普勒定律不仅适用于行星,也适用于卫星,此时比值 k 是由行星质量决定的另一恒量.
(2)行星的轨道都跟圆近似,因此计算时可以认为行星是做匀速圆周运动.
中学阶段对天体运动的近似处理:行星绕太阳运动的轨道十分接近圆,太阳处在圆心;行星绕太阳近似做匀速圆周运动;所有行星轨道半径的三次方跟它的公转周期的二次方的比值都相等。
(3)开普勒定律是总结行星运动的观察结果而归纳出来的规律,它们每一条都是经验定律,都是从观察行星运动所取得的资料中总结出来的.
关于行星围绕太阳运动的各种解释
证明了如果行星运动的轨道是椭圆.它所受的太阳引力大小跟行星到太阳的距离的二次方成反比。
牛顿
开普勒
笛卡尔
胡克、哈雷
受到了来自太阳的类似于磁力的作用
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,其所受的引力大小跟行星到太阳的距离的二次方成反比。
万有引力定律的建立
太阳吸引行星,行星也吸引太阳,引力相等
而
带入上式
牛二
开三
牛三
即
r
m
M
建模
质点
匀速圆周运动
万有引力定律
(G为引力常量)
任何两个物体之间都存在相互作用的引力,引力的大小与这两个物体的质量的乘积成正比,与这两个物体之间的距离的平方成反比。
公式的适用条件:
两质点间的万有引力
两质量分布均匀球体,r 指球心间的距离
一均匀球体与一质点
r
m1
m2
引力常量
太阳质量约为2×1030 kg,地球质量约为6×1024 kg,两者相距1.5×1011m,它们之间的引力多大?
3.6×1022N(可以把直径是9000km的钢柱拉断!)
?
两个质量都为50kg的均匀球体,相距5m,它们之间的引力是多大?
6.67×10-9N(一粒芝麻重的几十万分之一!)
1.要使两物体间的万有引力减小到原来的1/4,下列办法不可采用的是( )
A.使两物体的质量各减小一半,距离不变
B.使其中一个物体的质量减小到原来的1/4,距离不变
C.使两物体间的距离增大为原来的2倍,质量不变
D.使两物体间的距离和质量都减为原来的1/4
3.两个大小相同的实心匀质小铁球,紧靠在一起时它们之间的万有引力为F;若两个半径为小铁球2倍的实心均匀大铁球紧靠在一起,则它们之间的万有引力为( )
A.2F B.4F C.8F D.16F
4、如图所示,在半径为R的铅球中挖出一个球形空穴,空穴直径为R且与铅球相切,并通过铅球的球心。在未挖出空穴前铅球质量为M。求挖出空穴后的铅球与距铅球球心距离为d、质量为m的小球(可视为质点)间的万有引力大小。
谢 谢
第一节
万有引力定律
在浩瀚的宇宙中有无数大小不一、形态各异的天体,如月亮、地球、太阳、夜空中的星星。
人们对行星运动的认识过程是漫长复杂的,历史上有过不同的看法,科学家对此进行了不懈的探索,通过本节内容的学习,将使我们正确地认识行星的运动。
古人对地球的认识
古人根据有限范围内的观察(如日月星辰东升西落、远处天壤相接等),得出“天圆地方”之类的想法。
地心说与日心说
地
心
说
托 勒 密
日
心
说
哥白尼
第谷
开普勒
德国天文学家,第谷是他的
导师(1571—1630)在前人大量观测数据的基础上进一步完善了日心说。
行星三大定律
丹麦天文学家第谷(1546—1601),坚持对天体进行系统观测20余年,获得了大量精确资料
开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上.
开普勒行星运动定律
开普勒第二定律(面积定律):对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积.
远日点速度慢
近日点速度快
八大行星绕太阳运动的有关数据
a 是年的单位符号。
偏心率 e是椭圆扁平程度的量度,等于椭圆两焦点间的距离与长轴长度的比值。圆是椭圆的特例,偏心率为0。
开普勒第三定律(周期定律):所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.
表达式:
r3
T2
= k
半长轴
行星绕太阳公转的周期
k跟中心天体质量相关,与环绕天体无关
开普勒是用数学公式表达物理定律并最早获得成功的人之一。从此数学公式就成为表达物理学定律的基本方式。
温馨提示:
(1)开普勒定律不仅适用于行星,也适用于卫星,此时比值 k 是由行星质量决定的另一恒量.
(2)行星的轨道都跟圆近似,因此计算时可以认为行星是做匀速圆周运动.
中学阶段对天体运动的近似处理:行星绕太阳运动的轨道十分接近圆,太阳处在圆心;行星绕太阳近似做匀速圆周运动;所有行星轨道半径的三次方跟它的公转周期的二次方的比值都相等。
(3)开普勒定律是总结行星运动的观察结果而归纳出来的规律,它们每一条都是经验定律,都是从观察行星运动所取得的资料中总结出来的.
关于行星围绕太阳运动的各种解释
证明了如果行星运动的轨道是椭圆.它所受的太阳引力大小跟行星到太阳的距离的二次方成反比。
牛顿
开普勒
笛卡尔
胡克、哈雷
受到了来自太阳的类似于磁力的作用
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,其所受的引力大小跟行星到太阳的距离的二次方成反比。
万有引力定律的建立
太阳吸引行星,行星也吸引太阳,引力相等
而
带入上式
牛二
开三
牛三
即
r
m
M
建模
质点
匀速圆周运动
万有引力定律
(G为引力常量)
任何两个物体之间都存在相互作用的引力,引力的大小与这两个物体的质量的乘积成正比,与这两个物体之间的距离的平方成反比。
公式的适用条件:
两质点间的万有引力
两质量分布均匀球体,r 指球心间的距离
一均匀球体与一质点
r
m1
m2
引力常量
太阳质量约为2×1030 kg,地球质量约为6×1024 kg,两者相距1.5×1011m,它们之间的引力多大?
3.6×1022N(可以把直径是9000km的钢柱拉断!)
?
两个质量都为50kg的均匀球体,相距5m,它们之间的引力是多大?
6.67×10-9N(一粒芝麻重的几十万分之一!)
1.要使两物体间的万有引力减小到原来的1/4,下列办法不可采用的是( )
A.使两物体的质量各减小一半,距离不变
B.使其中一个物体的质量减小到原来的1/4,距离不变
C.使两物体间的距离增大为原来的2倍,质量不变
D.使两物体间的距离和质量都减为原来的1/4
3.两个大小相同的实心匀质小铁球,紧靠在一起时它们之间的万有引力为F;若两个半径为小铁球2倍的实心均匀大铁球紧靠在一起,则它们之间的万有引力为( )
A.2F B.4F C.8F D.16F
4、如图所示,在半径为R的铅球中挖出一个球形空穴,空穴直径为R且与铅球相切,并通过铅球的球心。在未挖出空穴前铅球质量为M。求挖出空穴后的铅球与距铅球球心距离为d、质量为m的小球(可视为质点)间的万有引力大小。
谢 谢
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
