第18章平行四边形——三角形的中位线 章末综合基础达标测试题(含解析)2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 第18章平行四边形——三角形的中位线 章末综合基础达标测试题(含解析)2023—2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 313.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 22:50:15 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学下册《第18章平行四边形——三角形的中位线》
章末综合基础达标测试题(附答案)
一、单选题(满分40分)
1.顺次连接四边形四边的中点所得的四边形为矩形,则四边形一定满足( )
A. B. C. D.
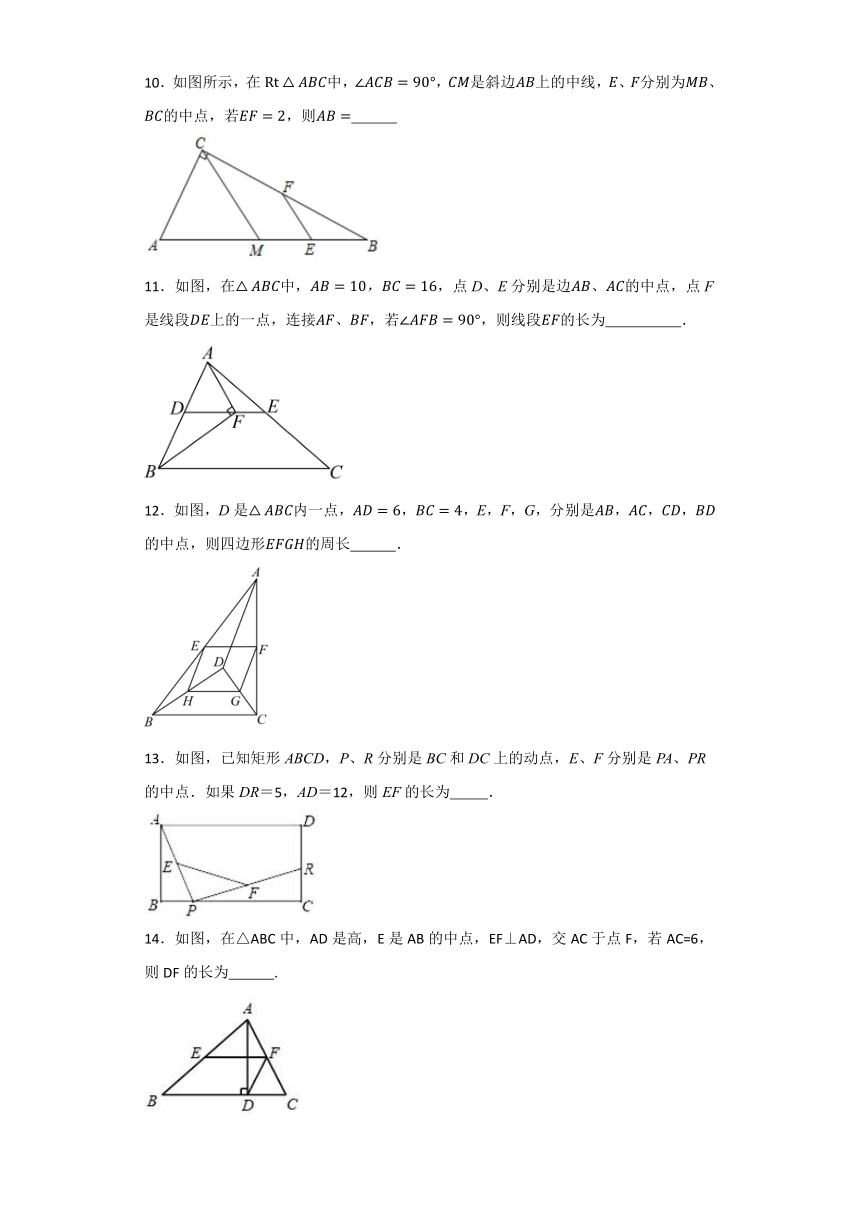
2.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到和的中点D、E,测量得米,则A、B两点间的距离为( )
A.30米 B.32米 C.36米 D.48米
3.在中,,,,点,,分别为边,,的中点,则的周长为( )
A. B. C. D.
4.如图,△ABC中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( )
A.13 B.15 C.17 D.19
5.如图,在菱形ABCD中,对角线AC与BD相交于点O,且E为BC中点,AD=8cm,则OE的长为( ).
A.8cm B.6cm C.4cm D.3cm
6.如图,在中,D,E,F分别是边,,的中点,连接,,,,,则下列说法正确的是( )
A.是的中位线 B.是的中位线
C.是的中位线 D.DF是的中位线
7.如图,点,为定点,定直线,是上一动点,点,分别为,的中点,对于下列各值:①线段的长;②的周长;③的大小;④直线,之间的距离.其中会随点的移动而不改变的是( )
A.①② B.①④ C.②③ D.③④
8.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
A.4 B.6 C.8 D.10
二、填空题(满分40分)
9.如图,中,,,D、E分别是、的中点,则 , .
10.如图所示,在中,,是斜边上的中线,、分别为、的中点,若,则
11.如图,在中,,点D、E分别是边的中点,点F是线段上的一点,连接,若,则线段的长为 .
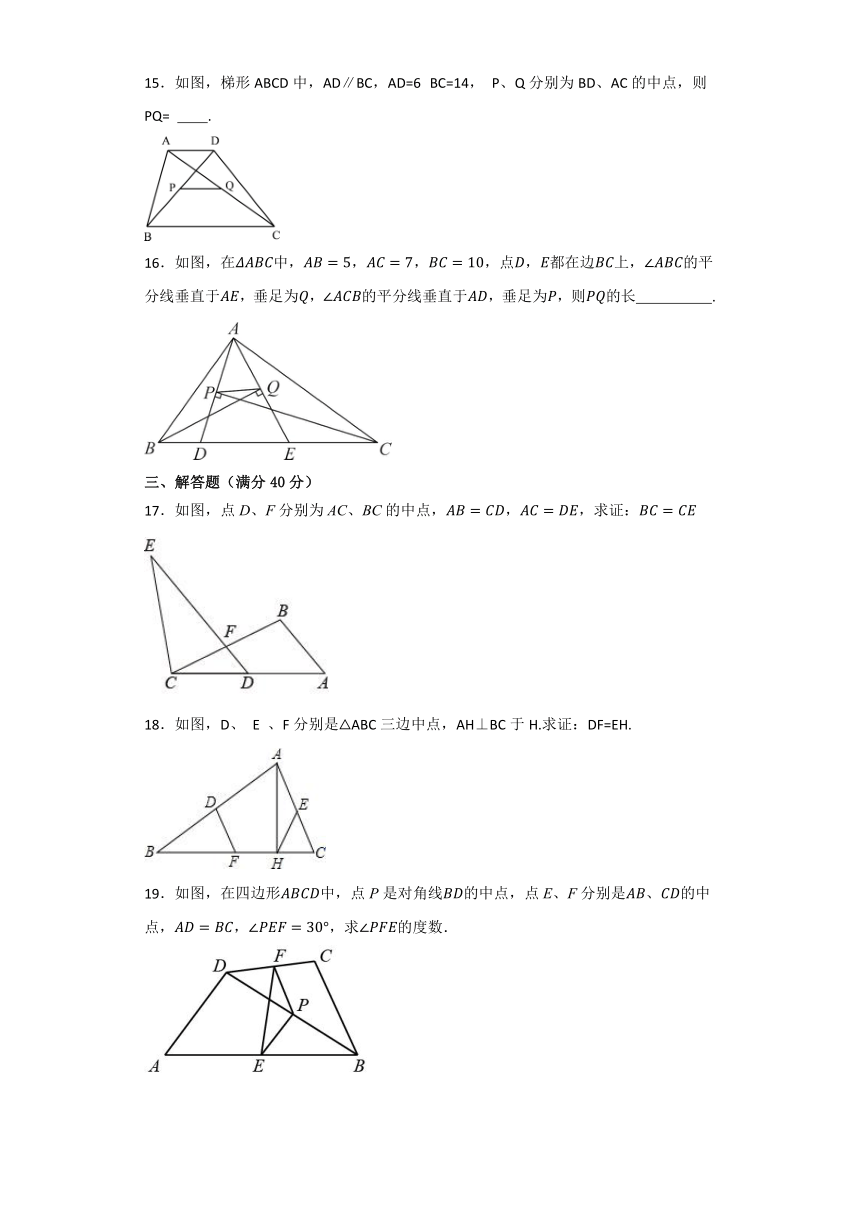
12.如图,D是内一点,,,E,F,G,分别是,,,的中点,则四边形的周长 .
13.如图,已知矩形ABCD,P、R分别是BC和DC上的动点,E、F分别是PA、PR的中点.如果DR=5,AD=12,则EF的长为 .
14.如图,在△ABC中,AD是高,E是AB的中点,EF⊥AD,交AC于点F,若AC=6,则DF的长为 .
15.如图,梯形ABCD中,AD∥BC,AD=6 BC=14, P、Q分别为BD、AC的中点,则PQ= .
16.如图,在中,,,,点,都在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,则的长 .
三、解答题(满分40分)
17.如图,点D、F分别为AC、BC的中点,,,求证:
18.如图,D、 E 、F分别是△ABC三边中点,AH⊥BC于H.求证:DF=EH.
19.如图,在四边形中,点P是对角线的中点,点E、F分别是、的中点,,,求的度数.
20.如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
21.(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
参考答案
1.解:由于E、F、G、H分别是的中点,
根据三角形中位线定理得:,
∵四边形是矩形,即,
∴,
故选:B.
2.解:∵D、E分别是、中点,
∴是的中位线,
∴,
∵米,
∴米,
∴A、B两点间的距离为32米.
故选:B
3.解:∵点D、E、F分别是边的中点,
,,是三角形的中位线,
,,,
的周长,
故选:C.
4.解:点D、E、F分别是AB、AC、BC的中点,
DE、EF均为的中位线,
,,
AB=10,BC=9,
,,
四边形DBFE的周长.
故选:D.
5.解:∵四边形ABCD是菱形,
∴AO=CO,AB=AD=8cm,
∵E为CB的中点,
∴OE是△ABC的中位线,
∴BA=2OE,
∴OE=4cm.
故选:C.
6.解:∵D,E,F分别是边,,的中点.
∴DE、EF、FD是的中位线.
A:AE是的中线,不符合题意.
B:EF是的中位线,符合题意.
C: 是的中线,不符合题意.
D:DF是的中线,不符合题意.
故选:B
7.解:∵点,分别为,的中点,
∴,,
∴线段的长不变,直线,之间的距离不变,故①④符合题意,
而、的长随点的运动而改变,的大小随点的运动而改变,故②③不符合题意;
故选:B.
8.解:平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,即DE最小.
∵OD⊥BC,BC⊥AB,
∴OD∥AB,
又∵OC=OA,
∴OD是△ABC的中位线,
∴OD=AB=3,
∴DE=2OD=6.
故选B.
9. 解:∵D、E分别是、的中点,
∴,,
∴,
故答案为:;.
10.解:∵,是斜边上的中线,
∴CM=AM=BM=,
∵、分别为、的中点,
∴EF为△BCM的中位线,
∴CM=2EF,
∵,
∴CM=2EF=4,
∴CM==4,
∴AB=8,
故答案为:8.
11.解:∵,点D是的中点,
∴,
∵D、E分别是,的中点,
∴,
∴,
故答案为3.
12.解:、、、分别是、、、的中点,
,,
,,
,,
四边形的周长是.
故答案为:.
13.解:∵∠D=90°,DR=5,AD=12,
∴AR==13,
∵E、F分别是PA、PR的中点,
∴EF=AR=6.5,
故答案为6.5.
14.解:∵AD是高,E是AB的中点,EF⊥AD,
∴EF是△ABC的中位线,
∴F点是AC中点,
∵AD是高,
∴△ACD是直角三角形,
∴DF=AC=3,
故填:3.
15.解:连接DQ,并延长交BC于点E,
∵AD∥BC,
∴∠DAQ=∠ECQ,
在△ADQ和△CEQ中,
,
∴△ADQ≌△CEQ(ASA),
∴DQ=EQ,CE=AD=6,
∴BE=BC-CE=14-6=8,
∵BP=DP,
∴PQ=BE=4.
故答案为4.
16.解:在△ABQ和△EBQ中,
,
∴△ABQ≌△EBQ(ASA),
∴BE=AB=5,AQ=QE,
同理可求CD=AC=7,AP=PD,
∴DE=CD-CE=CD-(BC-BE)=2,
∵AP=PD,AQ=QE,
∴PQ=DE=1,
故答案为1.
17.证明:∵点分别为的中点,
是的中位线,
∴,
∴,
在和中,,
∴,
∴.
18.证明:∵D、E 、F分别是△ABC三边中点,
∴DF是△ABC的中位线,
∴DF=AC,
∵AH⊥BC于H,E是AC的中点,
∴EH=AC,
∴DF=EH.
19.解:∵在四边形中,P是对角线的中点,E,F分别是、的中点,
∴,分别是与的中位线,
∴,,
∵,
∴,
故是等腰三角形,
∵,
∴.
20.(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
21.解:
(1) 证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=AB,FH∥CD,FH=CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2) 如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=AB=CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=.
故答案为(1)解析;(2)OE=.
章末综合基础达标测试题(附答案)
一、单选题(满分40分)
1.顺次连接四边形四边的中点所得的四边形为矩形,则四边形一定满足( )
A. B. C. D.
2.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到和的中点D、E,测量得米,则A、B两点间的距离为( )
A.30米 B.32米 C.36米 D.48米
3.在中,,,,点,,分别为边,,的中点,则的周长为( )
A. B. C. D.
4.如图,△ABC中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( )
A.13 B.15 C.17 D.19
5.如图,在菱形ABCD中,对角线AC与BD相交于点O,且E为BC中点,AD=8cm,则OE的长为( ).
A.8cm B.6cm C.4cm D.3cm
6.如图,在中,D,E,F分别是边,,的中点,连接,,,,,则下列说法正确的是( )
A.是的中位线 B.是的中位线
C.是的中位线 D.DF是的中位线
7.如图,点,为定点,定直线,是上一动点,点,分别为,的中点,对于下列各值:①线段的长;②的周长;③的大小;④直线,之间的距离.其中会随点的移动而不改变的是( )
A.①② B.①④ C.②③ D.③④
8.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
A.4 B.6 C.8 D.10
二、填空题(满分40分)
9.如图,中,,,D、E分别是、的中点,则 , .
10.如图所示,在中,,是斜边上的中线,、分别为、的中点,若,则
11.如图,在中,,点D、E分别是边的中点,点F是线段上的一点,连接,若,则线段的长为 .
12.如图,D是内一点,,,E,F,G,分别是,,,的中点,则四边形的周长 .
13.如图,已知矩形ABCD,P、R分别是BC和DC上的动点,E、F分别是PA、PR的中点.如果DR=5,AD=12,则EF的长为 .
14.如图,在△ABC中,AD是高,E是AB的中点,EF⊥AD,交AC于点F,若AC=6,则DF的长为 .
15.如图,梯形ABCD中,AD∥BC,AD=6 BC=14, P、Q分别为BD、AC的中点,则PQ= .
16.如图,在中,,,,点,都在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,则的长 .
三、解答题(满分40分)
17.如图,点D、F分别为AC、BC的中点,,,求证:
18.如图,D、 E 、F分别是△ABC三边中点,AH⊥BC于H.求证:DF=EH.
19.如图,在四边形中,点P是对角线的中点,点E、F分别是、的中点,,,求的度数.
20.如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
21.(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
参考答案
1.解:由于E、F、G、H分别是的中点,
根据三角形中位线定理得:,
∵四边形是矩形,即,
∴,
故选:B.
2.解:∵D、E分别是、中点,
∴是的中位线,
∴,
∵米,
∴米,
∴A、B两点间的距离为32米.
故选:B
3.解:∵点D、E、F分别是边的中点,
,,是三角形的中位线,
,,,
的周长,
故选:C.
4.解:点D、E、F分别是AB、AC、BC的中点,
DE、EF均为的中位线,
,,
AB=10,BC=9,
,,
四边形DBFE的周长.
故选:D.
5.解:∵四边形ABCD是菱形,
∴AO=CO,AB=AD=8cm,
∵E为CB的中点,
∴OE是△ABC的中位线,
∴BA=2OE,
∴OE=4cm.
故选:C.
6.解:∵D,E,F分别是边,,的中点.
∴DE、EF、FD是的中位线.
A:AE是的中线,不符合题意.
B:EF是的中位线,符合题意.
C: 是的中线,不符合题意.
D:DF是的中线,不符合题意.
故选:B
7.解:∵点,分别为,的中点,
∴,,
∴线段的长不变,直线,之间的距离不变,故①④符合题意,
而、的长随点的运动而改变,的大小随点的运动而改变,故②③不符合题意;
故选:B.
8.解:平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,即DE最小.
∵OD⊥BC,BC⊥AB,
∴OD∥AB,
又∵OC=OA,
∴OD是△ABC的中位线,
∴OD=AB=3,
∴DE=2OD=6.
故选B.
9. 解:∵D、E分别是、的中点,
∴,,
∴,
故答案为:;.
10.解:∵,是斜边上的中线,
∴CM=AM=BM=,
∵、分别为、的中点,
∴EF为△BCM的中位线,
∴CM=2EF,
∵,
∴CM=2EF=4,
∴CM==4,
∴AB=8,
故答案为:8.
11.解:∵,点D是的中点,
∴,
∵D、E分别是,的中点,
∴,
∴,
故答案为3.
12.解:、、、分别是、、、的中点,
,,
,,
,,
四边形的周长是.
故答案为:.
13.解:∵∠D=90°,DR=5,AD=12,
∴AR==13,
∵E、F分别是PA、PR的中点,
∴EF=AR=6.5,
故答案为6.5.
14.解:∵AD是高,E是AB的中点,EF⊥AD,
∴EF是△ABC的中位线,
∴F点是AC中点,
∵AD是高,
∴△ACD是直角三角形,
∴DF=AC=3,
故填:3.
15.解:连接DQ,并延长交BC于点E,
∵AD∥BC,
∴∠DAQ=∠ECQ,
在△ADQ和△CEQ中,
,
∴△ADQ≌△CEQ(ASA),
∴DQ=EQ,CE=AD=6,
∴BE=BC-CE=14-6=8,
∵BP=DP,
∴PQ=BE=4.
故答案为4.
16.解:在△ABQ和△EBQ中,
,
∴△ABQ≌△EBQ(ASA),
∴BE=AB=5,AQ=QE,
同理可求CD=AC=7,AP=PD,
∴DE=CD-CE=CD-(BC-BE)=2,
∵AP=PD,AQ=QE,
∴PQ=DE=1,
故答案为1.
17.证明:∵点分别为的中点,
是的中位线,
∴,
∴,
在和中,,
∴,
∴.
18.证明:∵D、E 、F分别是△ABC三边中点,
∴DF是△ABC的中位线,
∴DF=AC,
∵AH⊥BC于H,E是AC的中点,
∴EH=AC,
∴DF=EH.
19.解:∵在四边形中,P是对角线的中点,E,F分别是、的中点,
∴,分别是与的中位线,
∴,,
∵,
∴,
故是等腰三角形,
∵,
∴.
20.(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
21.解:
(1) 证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=AB,FH∥CD,FH=CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2) 如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=AB=CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=.
故答案为(1)解析;(2)OE=.
