12.2三角形全等的判定(第3课时)
文档属性
| 名称 | 12.2三角形全等的判定(第3课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-19 00:00:00 | ||
图片预览



文档简介
课件26张PPT。12.2 三角形全等的判定
(第3课时)1.什么是全等三角形?2.你学了哪几种判定两个三角形全等的方法?边边边(SSS)和边角边(SAS)一、问题引入 二、问题引领:阅读课本第39页至第41页内容,思考以下问题: 1、在39页的探究4中,是先画边还是先画角?为什么?
2、在例3中是如何创造条件的?运用了哪种判定方法?
3、有例4可以得到三角形全等的第四种判定方法,是什么?
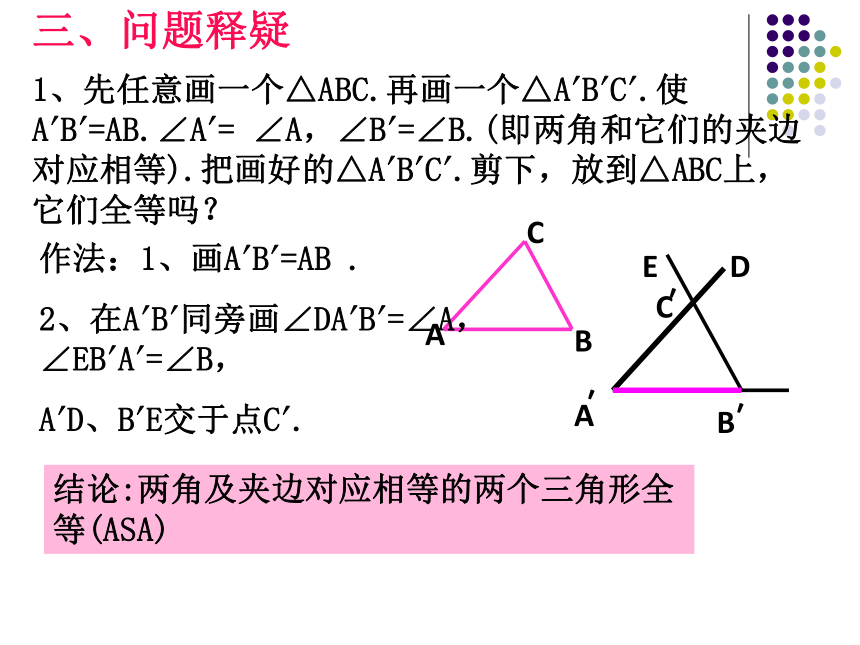
4、总结学过的三角形全等的判定方法。结论:两角及夹边对应相等的两个三角形全等(ASA)A′EDCB′′1、先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A,∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?作法:1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A,∠EB′A′=∠B,
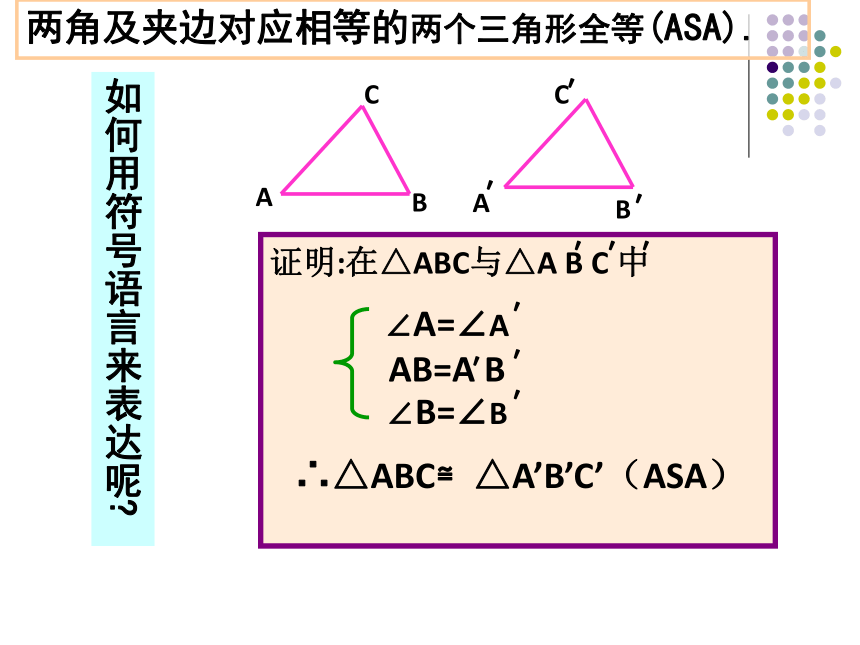
A′D、B′E交于点C′.三、问题释疑如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).例1 、AB=AC,∠B=∠C,(1)那么△ABE
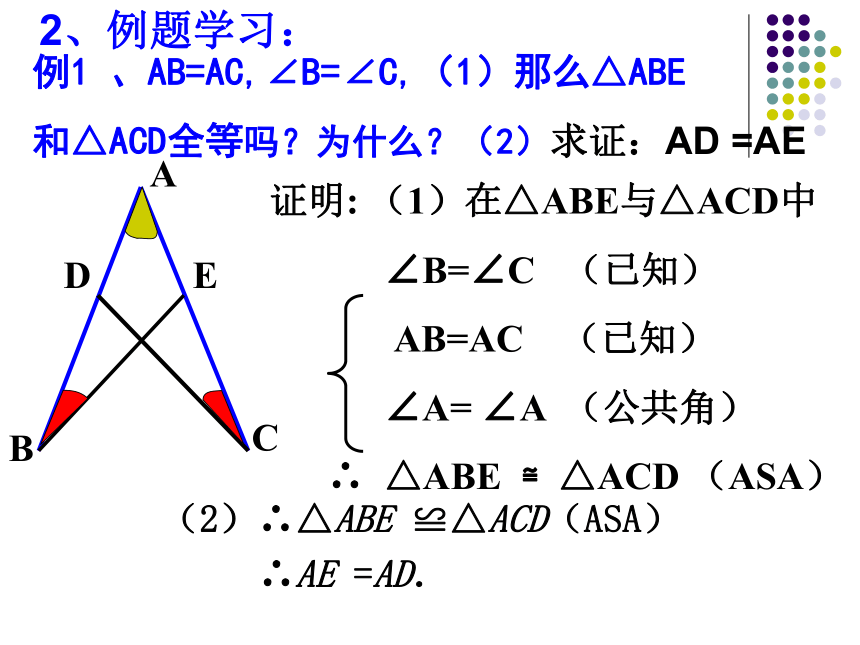
和△ACD全等吗?为什么?(2)求证:AD =AE证明: (1)在△ABE与△ACD中
∠B=∠C (已知)
AB=AC (已知)
∠A= ∠A (公共角)
∴ △ABE ≌△ACD (ASA) 2、例题学习:(2)∴△ABE ≌△ACD(ASA)
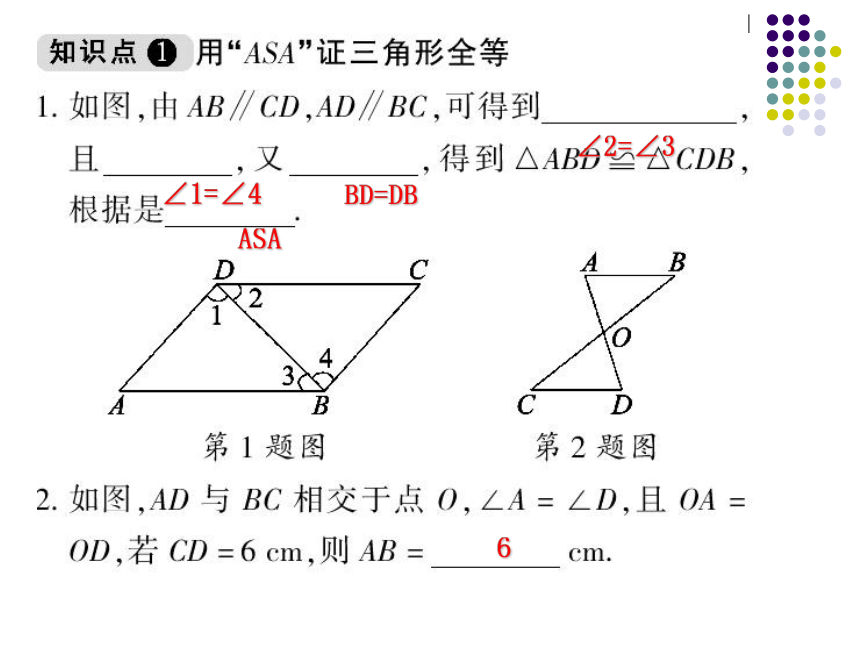
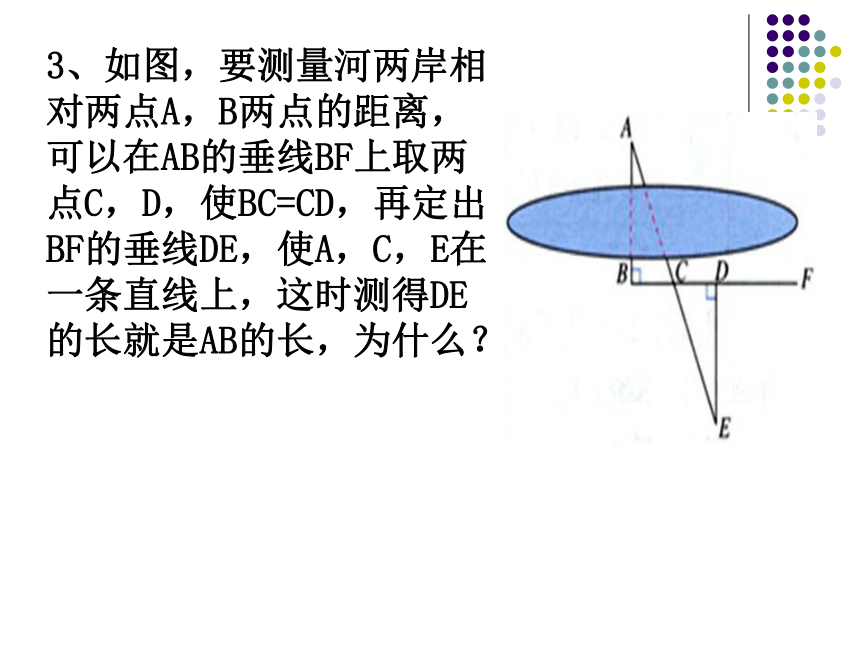
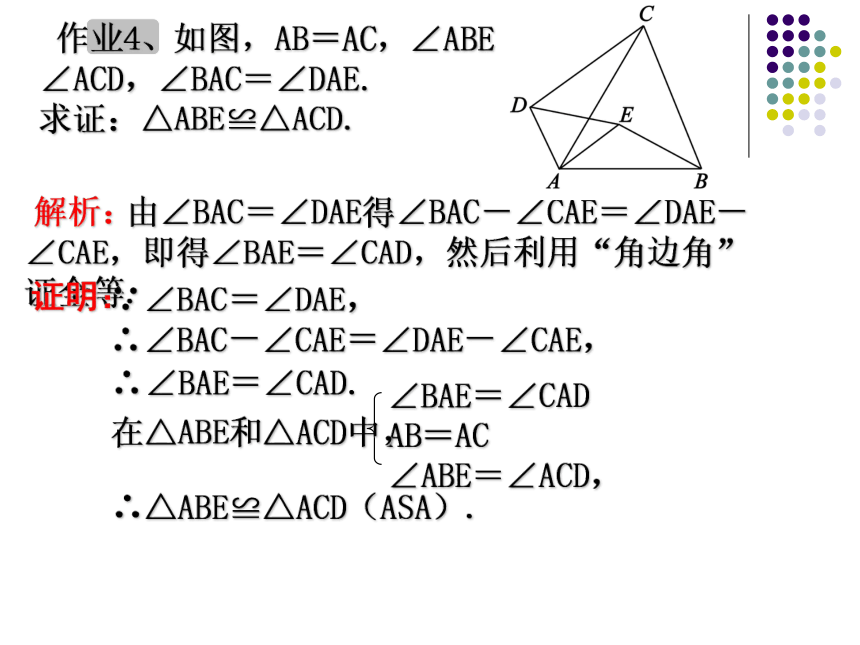
∴AE =AD.∠2=∠36∠1=∠4BD=DBASA3、如图,要测量河两岸相对两点A,B两点的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么? 作业4、如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.解析: 由∠BAC=∠DAE得∠BAC-∠CAE=∠DAE-∠CAE,即得∠BAE=∠CAD,然后利用“角边角”证全等.证明:∵∠BAC=∠DAE,∴∠BAC-∠CAE=∠DAE-∠CAE,∠BAE=∠CAD
AB=AC
∠ABE=∠ACD,∴∠BAE=∠CAD.在△ABE和△ACD中,∴△ABE≌△ACD(ASA).ACBEDF分析:能否转化为ASA?证明:∵ ∠A=∠D, ∠B=∠E(已知) ∴∠C=∠F(三角形内角和定理)∠B=∠E
BC=EF
∠C=∠F在△ABC和△DEF中∴△ABC≌△DEF(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)例2:在△ABC和△DEF中, ∠A=∠D,∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?1.如图,AD=AE,∠B=∠C,那么BE和CD
相等么?为什么?变一变BE=CD你还能得出其他
什么结论?O如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)1.已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD12证明:三、练习12ABCD2、如图,AB⊥BC, AD⊥DC ,∠1= ∠2,
求证:AB=ADAAS△ABO△DCOAASBB有几种填法?AC=BDASACO=DOAASAO=BOAAS证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,例3、 如图,AE⊥BE,AD⊥DC,CD =
BE,∠DAB =∠EAC.求证:AB =AC. ∴ △ADC ≌△AEB(AAS).
∴ AC =AB.练习1、E,F 在线段AC上,AD∥CB,
AE = CF.若∠B =∠D。
求证:DF =BE.证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF -EF=CE-EF.
即AF =CE变式:若将条件 “∠B =∠D”变为“DF∥BE”,
那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.2、如图:已知AB∥DE,AC∥DF,BE=CF。
求证:△ABC≌△DEF。证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA)∵ AB∥DE AC∥DF (已知) ∴ ∠B=∠DEF , ∠ACB=∠F证明:∠B=∠D
∠ACB=∠ECD
AC=EC,∴△ABC≌△EDC(AAS),∴BC=DC.在△ABC和△EDC中,∵∠BCE=∠DCA,∴∠BCE+∠ECA=∠DCA+∠ECA,∴∠ACB=∠ECD,例4、如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?1、边边边(SSS):三边对应相等
2、边角边(SAS):两边及夹角对应相等
3、角边角(ASA):ASA两角夹边对应相等
4、角角边(AAS):两角及一角的对边对应相等判定三角形全等的四种方法,它们分别是:
(第3课时)1.什么是全等三角形?2.你学了哪几种判定两个三角形全等的方法?边边边(SSS)和边角边(SAS)一、问题引入 二、问题引领:阅读课本第39页至第41页内容,思考以下问题: 1、在39页的探究4中,是先画边还是先画角?为什么?
2、在例3中是如何创造条件的?运用了哪种判定方法?
3、有例4可以得到三角形全等的第四种判定方法,是什么?
4、总结学过的三角形全等的判定方法。结论:两角及夹边对应相等的两个三角形全等(ASA)A′EDCB′′1、先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A,∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?作法:1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A,∠EB′A′=∠B,
A′D、B′E交于点C′.三、问题释疑如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).例1 、AB=AC,∠B=∠C,(1)那么△ABE
和△ACD全等吗?为什么?(2)求证:AD =AE证明: (1)在△ABE与△ACD中
∠B=∠C (已知)
AB=AC (已知)
∠A= ∠A (公共角)
∴ △ABE ≌△ACD (ASA) 2、例题学习:(2)∴△ABE ≌△ACD(ASA)
∴AE =AD.∠2=∠36∠1=∠4BD=DBASA3、如图,要测量河两岸相对两点A,B两点的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么? 作业4、如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.解析: 由∠BAC=∠DAE得∠BAC-∠CAE=∠DAE-∠CAE,即得∠BAE=∠CAD,然后利用“角边角”证全等.证明:∵∠BAC=∠DAE,∴∠BAC-∠CAE=∠DAE-∠CAE,∠BAE=∠CAD
AB=AC
∠ABE=∠ACD,∴∠BAE=∠CAD.在△ABE和△ACD中,∴△ABE≌△ACD(ASA).ACBEDF分析:能否转化为ASA?证明:∵ ∠A=∠D, ∠B=∠E(已知) ∴∠C=∠F(三角形内角和定理)∠B=∠E
BC=EF
∠C=∠F在△ABC和△DEF中∴△ABC≌△DEF(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)例2:在△ABC和△DEF中, ∠A=∠D,∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?1.如图,AD=AE,∠B=∠C,那么BE和CD
相等么?为什么?变一变BE=CD你还能得出其他
什么结论?O如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)1.已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD12证明:三、练习12ABCD2、如图,AB⊥BC, AD⊥DC ,∠1= ∠2,
求证:AB=ADAAS△ABO△DCOAASBB有几种填法?AC=BDASACO=DOAASAO=BOAAS证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,例3、 如图,AE⊥BE,AD⊥DC,CD =
BE,∠DAB =∠EAC.求证:AB =AC. ∴ △ADC ≌△AEB(AAS).
∴ AC =AB.练习1、E,F 在线段AC上,AD∥CB,
AE = CF.若∠B =∠D。
求证:DF =BE.证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF -EF=CE-EF.
即AF =CE变式:若将条件 “∠B =∠D”变为“DF∥BE”,
那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.2、如图:已知AB∥DE,AC∥DF,BE=CF。
求证:△ABC≌△DEF。证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA)∵ AB∥DE AC∥DF (已知) ∴ ∠B=∠DEF , ∠ACB=∠F证明:∠B=∠D
∠ACB=∠ECD
AC=EC,∴△ABC≌△EDC(AAS),∴BC=DC.在△ABC和△EDC中,∵∠BCE=∠DCA,∴∠BCE+∠ECA=∠DCA+∠ECA,∴∠ACB=∠ECD,例4、如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?1、边边边(SSS):三边对应相等
2、边角边(SAS):两边及夹角对应相等
3、角边角(ASA):ASA两角夹边对应相等
4、角角边(AAS):两角及一角的对边对应相等判定三角形全等的四种方法,它们分别是:
