吉林省长春市师大附中新城学校2023-2024学年第二学期九年级数学第一次月考试题(无答案)
文档属性
| 名称 | 吉林省长春市师大附中新城学校2023-2024学年第二学期九年级数学第一次月考试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 528.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 15:19:02 | ||
图片预览


文档简介
东师附中新城学校九年级下学期第一次月考数学试题
时间:2小时 分数:120
一、选择题(每小题3分,共24分)
1. 如图,某葡萄采摘园采摘了A、B、C、D四筐葡萄,每筐葡萄以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,其中最接近标准质量的葡萄是( )
A. B. C. D.
2. 中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破23000000000户,数据23000000000用科学记数法表示为( )
A. B. C. D.
3. 某几何体的表面展开图如图所示,这个几何体是( )
A. 圆柱 B. 长方体 C. 四棱锥 D. 五棱锥
4. 为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过元.若每个篮球60元,每个足球30元,则篮球最多可购买( )个
A. 14 B. 15 C. 16 D. 17
5. 如图,小明在点处测得树的顶端仰角为,同时测得,则树的高度为( )
A. B. C. D.
6. 剪纸是我国民间艺术,入选“人类非物质文化遗产”,如图剪纸图案是一个中心对称图形,将其绕中心旋转一定角度后,依然与原图形重合,这个角度不可以是( )
A. B. C. D.
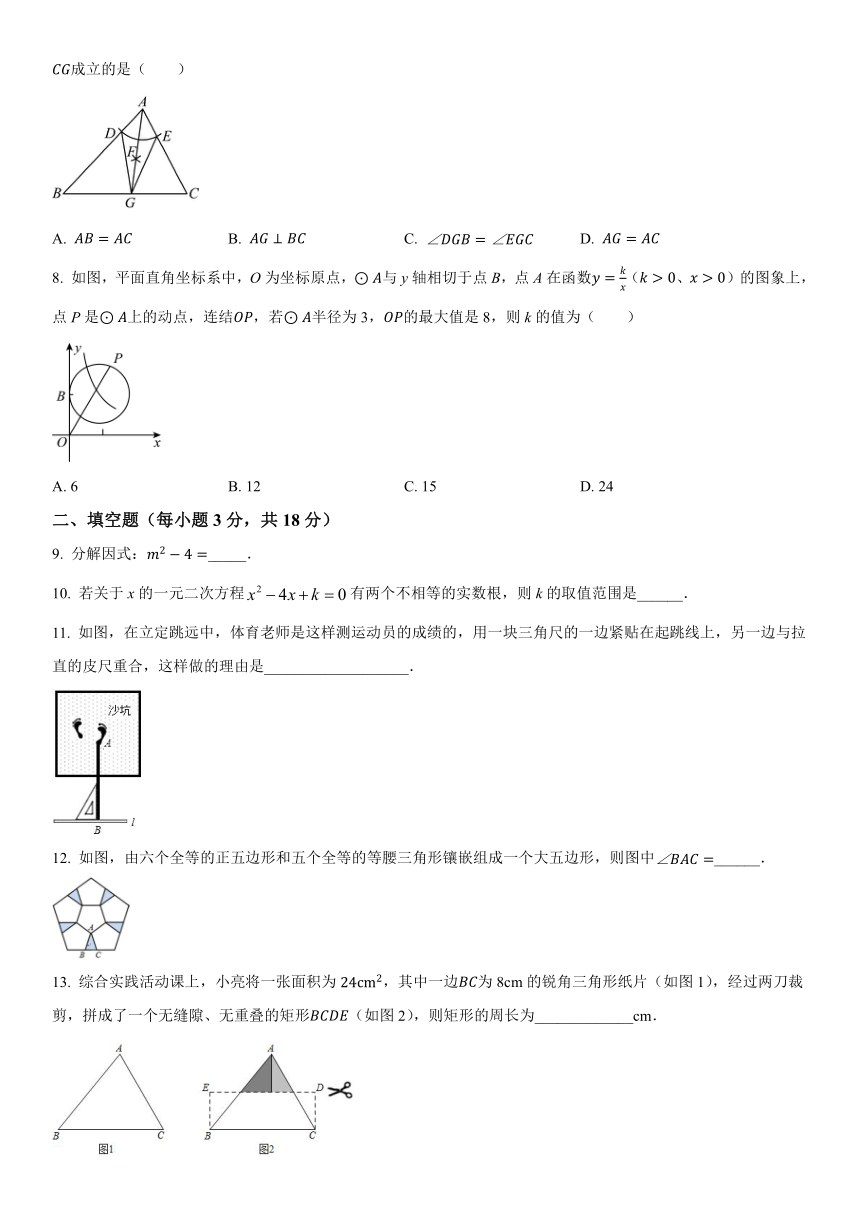
7. 如图,在中,以点A为圆心,适当长为半径画弧,分别交,于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于内一点F.连结并延长,交于点G.连结,.添加下列条件,不能使成立的是( )
A. B. C. D.
8. 如图,平面直角坐标系中,O为坐标原点,与y轴相切于点B,点A在函数(、)的图象上,点P是上的动点,连结,若半径为3,的最大值是8,则k的值为( )
A. 6 B. 12 C. 15 D. 24
二、填空题(每小题3分,共18分)
9. 分解因式:_____.
10. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
11. 如图,在立定跳远中,体育老师是这样测运动员的成绩的,用一块三角尺的一边紧贴在起跳线上,另一边与拉直的皮尺重合,这样做的理由是___________________.
12. 如图,由六个全等的正五边形和五个全等的等腰三角形镶嵌组成一个大五边形,则图中______.
13. 综合实践活动课上,小亮将一张面积为,其中一边为8cm的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形(如图2),则矩形的周长为_____________cm.
14. 如图,在平面直角坐标系中,O为坐标原点,点在抛物线上,点B是该抛物线的顶点,连结,以、为边向右侧作,则图中阴影部分图形的面积和为______.
二、解答题(本大题10小题,共78分)
15. 先化简.再求值:,其中.
16. 2023年10月26日,搭载三名航天员汤洪波、唐胜杰、江新林的神舟十七号载人飞船发射成功,某校为弘扬爱国主义精神,举办以航天员事迹为主题的演讲比赛.主题人物由抽卡片决定.现有三张不透明的卡片,卡片正面分别写着汤洪波、唐胜杰、江新林三位航天员的姓名,依次记作A,B,C,卡片除正面姓名不同外,其余均相同,三张卡片正面向下洗匀后,甲选手从中随机抽取一张卡片,记录航天员姓名后正面向下放回,洗匀后乙选手再从中随机抽取一张卡片,请用画树状图或列表的方法,求甲、乙两位选手演讲的主题人物是不同航天员的概率.
17. 某快递公司为提高配送效率,引进了甲、乙两种型号“分拣机器人”,已知甲型号每小时分拣数量比乙型号每小时分拣数量多50件,且甲型号分拣1000件与乙型号分拣800件所用时间相同,求乙型号分拣机器人每小时分拣的数量.
18. 某校计划更换校服款式,为调研学生对A,B两款校服满意度,随机抽取了20名同学试穿两款校服,对舒适性、性价比和时尚性进行评分(满分均为20分),并按照1:1:1的比计算综合评分.将数据(评分)进行整理、描述和分析.下面给出了部分信息.
a.A,B两款校服各项评分平均数(精确到0.1)如下:
款式 舒适性评分平均数 性价比评分平均数 时尚性评分平均数 综合评分平均数
A 19.5 19.6 10.2
B 19.2 18.5 10.4 16.0
b.不同评分对应的满意度如下表:
评分 0≤x<5 5≤x<10 10≤x<15 15≤x≤20
满意度 不满意 基本满意 满意 非常满意
c.A,B两款校服时尚性满意度人数分布统计图如图:
d.B校服时尚性评分在这一组的是:10,11,12,12,14;
根据以上信息,回答下列问题:
(1)在此次调研中,
① A校服综合评分平均数是否达到“非常满意”:______(填“是”或“否”);
② A校服时尚性满意度达到“非常满意”的人数为______;
(2)在此次调研中,B校服时尚性评分的中位数为______;
(3)在此次调研中,记A校服时尚性评分高于其平均数的人数为m,B校服时尚性评分高于其平均数的人数为n.比较m,n的大小,并说明理由.
19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,线段的端点均在格点上.只用无刻度的直尺按下列要求在给定的网格中画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以为一边画,使其面积为.
(2)在图②中以为一边画钝角,使其面积为4.
(3)在图③中以为一边画锐角,使其面积为4.
20. 如图,在四边形中,,,对角线、交于点O,平分,过点C作交延长线于点E.
(1)求证:四边形是菱形.
(2)若,,则四边形的面积为______.
21. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水,进水管每分钟的进水量和出水管每分钟的出水量始终不变,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,根据图象解答下列问题:
(1)进水管每分钟的进水量为______L;
(2)当时,求y与x之间的函数关系式;
(3)补全图象.
22. 【探究】如图①,是等边三角形,它内接于,点D是上任意一点(不与点B、C重合),连结、,求证:.
小明分析后发现,如图②,将绕点A顺时针旋转得到,再证明D、B、E三点共线,从而得到等边三角形,进而证得.
下面是小明的部分证明过程:
证明:∵绕点A顺时针旋转得到,
∴.
∵,∴.
∴D、B、E三点共线.
请你补全余下的证明过程.
【应用】如图①,是等边三角形,它内接于,点D是上任意一点(不与点B、C重合),连结、.若,则四边形的面积为______.
【拓展】如图③,等腰直角三角形内接于,,点D在上且位于直线下方,若的半径为2,则四边形的周长的最大值为______.
23. 如图,在矩形中,,.动点P从点A出发,以每秒2个单位长度速度沿折线向终点C运动,当点P出发后,连结,作,边交射线于点Q,连接.将沿翻折,得到.设点P的运动时间为t秒.
(1)用含t代数式表示的长.
(2)连结,求的最小值.
(3)当点E在矩形的边上时,求t的值.
(4)连结,当经过矩形的边的中点时,直接写出t的值.
24. 在平面直角坐标系中,O为坐标原点,抛物线经过点,其对称轴为直线,点P是此抛物线上的点,其横坐标为,连结,取的中点B,过点B作y轴的平行线交此抛物线于点Q,连结、.
(1)求此抛物线对应的函数关系式.
(2)当抛物线在点P与点Q之间的部分(包括点P和点Q)的图象对应的函数值y随x的增大而增大或y随x的增大而减小时,求m的取值范围.
(3)当的边与x轴平行时,求的面积.
(4)连结,当的面积等于此抛物线在点P与点Q之间的部分(包括点P和点Q)的最高点与最低点纵坐标的差时,直接写出m的值.
时间:2小时 分数:120
一、选择题(每小题3分,共24分)
1. 如图,某葡萄采摘园采摘了A、B、C、D四筐葡萄,每筐葡萄以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,其中最接近标准质量的葡萄是( )
A. B. C. D.
2. 中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破23000000000户,数据23000000000用科学记数法表示为( )
A. B. C. D.
3. 某几何体的表面展开图如图所示,这个几何体是( )
A. 圆柱 B. 长方体 C. 四棱锥 D. 五棱锥
4. 为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过元.若每个篮球60元,每个足球30元,则篮球最多可购买( )个
A. 14 B. 15 C. 16 D. 17
5. 如图,小明在点处测得树的顶端仰角为,同时测得,则树的高度为( )
A. B. C. D.
6. 剪纸是我国民间艺术,入选“人类非物质文化遗产”,如图剪纸图案是一个中心对称图形,将其绕中心旋转一定角度后,依然与原图形重合,这个角度不可以是( )
A. B. C. D.
7. 如图,在中,以点A为圆心,适当长为半径画弧,分别交,于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于内一点F.连结并延长,交于点G.连结,.添加下列条件,不能使成立的是( )
A. B. C. D.
8. 如图,平面直角坐标系中,O为坐标原点,与y轴相切于点B,点A在函数(、)的图象上,点P是上的动点,连结,若半径为3,的最大值是8,则k的值为( )
A. 6 B. 12 C. 15 D. 24
二、填空题(每小题3分,共18分)
9. 分解因式:_____.
10. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
11. 如图,在立定跳远中,体育老师是这样测运动员的成绩的,用一块三角尺的一边紧贴在起跳线上,另一边与拉直的皮尺重合,这样做的理由是___________________.
12. 如图,由六个全等的正五边形和五个全等的等腰三角形镶嵌组成一个大五边形,则图中______.
13. 综合实践活动课上,小亮将一张面积为,其中一边为8cm的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形(如图2),则矩形的周长为_____________cm.
14. 如图,在平面直角坐标系中,O为坐标原点,点在抛物线上,点B是该抛物线的顶点,连结,以、为边向右侧作,则图中阴影部分图形的面积和为______.
二、解答题(本大题10小题,共78分)
15. 先化简.再求值:,其中.
16. 2023年10月26日,搭载三名航天员汤洪波、唐胜杰、江新林的神舟十七号载人飞船发射成功,某校为弘扬爱国主义精神,举办以航天员事迹为主题的演讲比赛.主题人物由抽卡片决定.现有三张不透明的卡片,卡片正面分别写着汤洪波、唐胜杰、江新林三位航天员的姓名,依次记作A,B,C,卡片除正面姓名不同外,其余均相同,三张卡片正面向下洗匀后,甲选手从中随机抽取一张卡片,记录航天员姓名后正面向下放回,洗匀后乙选手再从中随机抽取一张卡片,请用画树状图或列表的方法,求甲、乙两位选手演讲的主题人物是不同航天员的概率.
17. 某快递公司为提高配送效率,引进了甲、乙两种型号“分拣机器人”,已知甲型号每小时分拣数量比乙型号每小时分拣数量多50件,且甲型号分拣1000件与乙型号分拣800件所用时间相同,求乙型号分拣机器人每小时分拣的数量.
18. 某校计划更换校服款式,为调研学生对A,B两款校服满意度,随机抽取了20名同学试穿两款校服,对舒适性、性价比和时尚性进行评分(满分均为20分),并按照1:1:1的比计算综合评分.将数据(评分)进行整理、描述和分析.下面给出了部分信息.
a.A,B两款校服各项评分平均数(精确到0.1)如下:
款式 舒适性评分平均数 性价比评分平均数 时尚性评分平均数 综合评分平均数
A 19.5 19.6 10.2
B 19.2 18.5 10.4 16.0
b.不同评分对应的满意度如下表:
评分 0≤x<5 5≤x<10 10≤x<15 15≤x≤20
满意度 不满意 基本满意 满意 非常满意
c.A,B两款校服时尚性满意度人数分布统计图如图:
d.B校服时尚性评分在这一组的是:10,11,12,12,14;
根据以上信息,回答下列问题:
(1)在此次调研中,
① A校服综合评分平均数是否达到“非常满意”:______(填“是”或“否”);
② A校服时尚性满意度达到“非常满意”的人数为______;
(2)在此次调研中,B校服时尚性评分的中位数为______;
(3)在此次调研中,记A校服时尚性评分高于其平均数的人数为m,B校服时尚性评分高于其平均数的人数为n.比较m,n的大小,并说明理由.
19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,线段的端点均在格点上.只用无刻度的直尺按下列要求在给定的网格中画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以为一边画,使其面积为.
(2)在图②中以为一边画钝角,使其面积为4.
(3)在图③中以为一边画锐角,使其面积为4.
20. 如图,在四边形中,,,对角线、交于点O,平分,过点C作交延长线于点E.
(1)求证:四边形是菱形.
(2)若,,则四边形的面积为______.
21. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水,进水管每分钟的进水量和出水管每分钟的出水量始终不变,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,根据图象解答下列问题:
(1)进水管每分钟的进水量为______L;
(2)当时,求y与x之间的函数关系式;
(3)补全图象.
22. 【探究】如图①,是等边三角形,它内接于,点D是上任意一点(不与点B、C重合),连结、,求证:.
小明分析后发现,如图②,将绕点A顺时针旋转得到,再证明D、B、E三点共线,从而得到等边三角形,进而证得.
下面是小明的部分证明过程:
证明:∵绕点A顺时针旋转得到,
∴.
∵,∴.
∴D、B、E三点共线.
请你补全余下的证明过程.
【应用】如图①,是等边三角形,它内接于,点D是上任意一点(不与点B、C重合),连结、.若,则四边形的面积为______.
【拓展】如图③,等腰直角三角形内接于,,点D在上且位于直线下方,若的半径为2,则四边形的周长的最大值为______.
23. 如图,在矩形中,,.动点P从点A出发,以每秒2个单位长度速度沿折线向终点C运动,当点P出发后,连结,作,边交射线于点Q,连接.将沿翻折,得到.设点P的运动时间为t秒.
(1)用含t代数式表示的长.
(2)连结,求的最小值.
(3)当点E在矩形的边上时,求t的值.
(4)连结,当经过矩形的边的中点时,直接写出t的值.
24. 在平面直角坐标系中,O为坐标原点,抛物线经过点,其对称轴为直线,点P是此抛物线上的点,其横坐标为,连结,取的中点B,过点B作y轴的平行线交此抛物线于点Q,连结、.
(1)求此抛物线对应的函数关系式.
(2)当抛物线在点P与点Q之间的部分(包括点P和点Q)的图象对应的函数值y随x的增大而增大或y随x的增大而减小时,求m的取值范围.
(3)当的边与x轴平行时,求的面积.
(4)连结,当的面积等于此抛物线在点P与点Q之间的部分(包括点P和点Q)的最高点与最低点纵坐标的差时,直接写出m的值.
同课章节目录
