高中数学人教A版(2019)必修2 第八章 8.6.2 直线与平面垂直(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 第八章 8.6.2 直线与平面垂直(第2课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 21:06:27 | ||
图片预览







文档简介
(共23张PPT)
第七章
8.6.2 直线与平面垂直(第2课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.理解直线与平面垂直的性质定理,并会用直线与平面垂直的性质定理证明相关问题; 1.几何直观素养和逻辑推理素养.
2.理解直线到平面的距离、两个平面间的距离的概念,并会求直线到平面的距离. 2.空间想象素养和逻辑推理素养.
温故知新
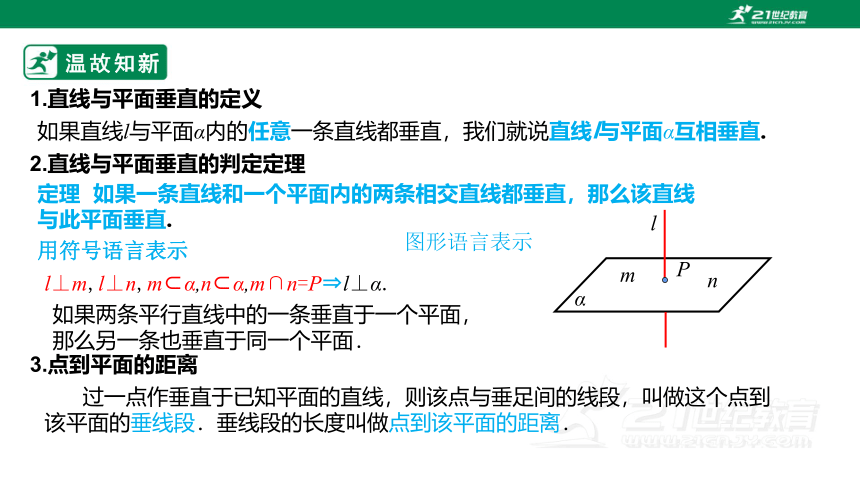
1.直线与平面垂直的定义
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.
2.直线与平面垂直的判定定理
定理 如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
用符号语言表示
l⊥m,l⊥n,m α,n α,m∩n=P l⊥α.
图形语言表示
α
P
l
m
n
如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面.
3.点到平面的距离
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段.垂线段的长度叫做点到该平面的距离.
新知引入
观察下列图片,你能发现什么线、面关系的规律吗?
下面我们研究直线与平面垂直的性质,即探究在直线a与平面α垂直的条件下能推出哪些结论.
根据已有经验,我们可以探究直线a与平面α内的直线关系. 但由定义, a与α内的所有直线垂直. 所以,可以探究a , α与其他直线或平面的关系.
我们知道,在平面内,垂直于同一条直线的两条直线平行 . 在空间中是否有类似的性质呢?
新知引入
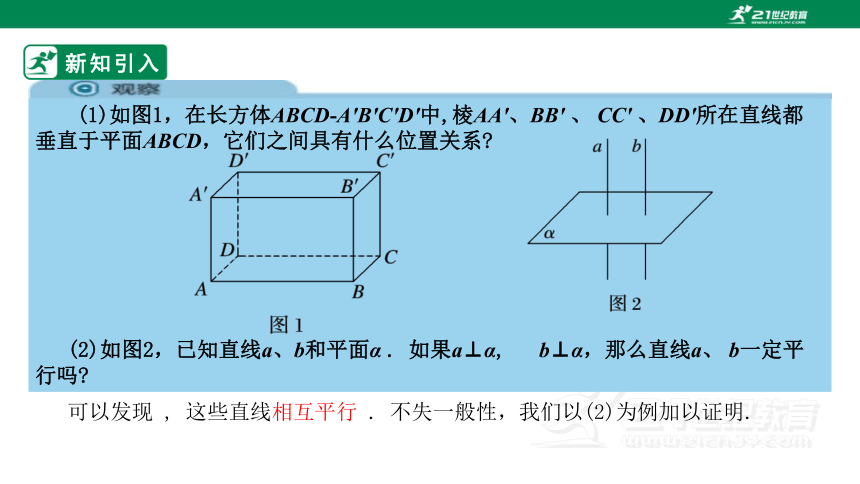
(1)如图1,在长方体ABCD-A′B′C′D′中,棱AA′、BB′ 、 CC′ 、DD′所在直线都垂直于平面ABCD,它们之间具有什么位置关系
(2)如图2,已知直线a、b和平面α . 如果a⊥α, b⊥α,那么直线a、 b一定平行吗
可以发现 , 这些直线相互平行 . 不失一般性,我们以(2)为例加以证明.
新知探究
如图,假设a与b不平行,且b∩α=O.
显然点O不在直线a上,所以点O与直线a可确定一个平面.
在该平面内过点O作直线b′//a, 则直线b与b'是相交于点O的两条不同直线,所以直线b与b'可确定平面β.
设α∩β=c, 则O∈c.
因为a⊥α, b⊥α,所以a⊥c, b⊥c.
又因为b′//a , 所以b'⊥c.
这样在平面β内,经过直线c上同一点O就有两条直线b、b′与c垂直,显然不可能.
因此 b//a.
由于无法把两条直线a、b归入到一个平面内,所以在定理的证明中,无法应用平面直线的判定知识,也无法应用基本事实4,在这种情况下我们采用了“反证法”.
a
b
α
O
b′
c
β
新知探究
这样,我们得到了直线与平面垂直的一条性质定理.
定理 垂直于同一个平面的两条直线平行.
符号语言表示
a⊥α, b⊥α a//b.
图形语言表示
作用:判断线线平行
线面垂直 线线平行
直线与平面垂直的性质定理告诉我们 , 可以由两条直线与一个平面垂直判定两条直线平行.直线与平面垂直的性质定理揭示了“平行”与“垂直”之间的内在联系.
新知探究
在a⊥α的条件下,如果平面α外的直线b与直线a垂直,你能得到什么结论 如果平面α与平面β平行,你又能得到什么结论
b
a
a⊥α,b⊥a,b α b//α.
a
a⊥α,α//β a⊥β.
α
β
a
在a⊥α的条件下,如果a⊥β,又能得到什么结论?
a⊥α,a⊥β α//β.
知新探究
【例1】如图,直线l平行于平面α,求证:直线l上各点到平面α的距离相等.
证明:
过直线l上任意两点A,B分别作平面α的垂线AA1,BB1,垂足分别为A1,B1.
∴AA1=BB1.
∵ AA1⊥α,BB1⊥α,
∴AA1//BB1.
∵l∥α,
∴l∥A1B1.
设直线AA1,BB1确定的平面为β,β∩α=A1B1,
∴四边形AA1B1B是矩形.
由A,B是直线l上任取的两点,可知直线l上各点到平面α的距离相等.
知新探究
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
a
α
由例1还可以进一步得出,
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
α
β
在棱柱、棱台的体积公式中,它们的高就是它们底面间的距离.
知新探究
【例2】推导棱台体积公式
其中S′,S分别是棱台的上、下底面面积,h是高.
解:
如图,延长棱台各侧棱交于一点P,得到截得棱台的棱锥.过点P作棱台下底面的垂线,分别交棱台的上、下底面于点O′,O,
∴棱台的体积
∴.
.
设截得棱台的棱锥的体积为V,去掉的棱锥的体积为V′,高为h′.则PO′=h′.
则PO垂直于棱台的上底面.从而O′O=h.
知新探究
【例2】推导棱台体积公式
其中S′,S分别是棱台的上、下底面面积,h是高.
解:
.
,
由棱台的上、下底面平行,棱台的上、下底面相似,并且
.
∴.
知新探究
【例3】如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.
证明:AE∥MN.
证明:
∵AD=AP,E是PD的中点,
∴AE⊥AB,
∵AB⊥平面PAD,AE 平面PAD,
又AB∥CD,
∴AE⊥PD.
∴AE⊥CD.
又CD∩PD=D,CD,PD 平面PCD,
∴AE⊥平面PCD.
∵MN⊥AB,AB∥CD,
∴MN⊥CD.
又∵MN⊥PC,PC∩CD=C,PC,CD 平面PCD,
∴MN⊥平面PCD,
∴AE∥MN.
知新探究
【例4】已知在长方体ABCD-A1B1C1D1中,棱AA1=12,AB=5.
⑴求点B1到平面A1BCD1的距离;
⑵求B1C1到平面A1BCD1的距离.
解:
∵AD=AP,E是PD的中点,
⑴如图,过点B1作B1E⊥A1B于点E.
由题意知BC⊥平面A1ABB1,且B1E 平面A1ABB1,
∴BC⊥B1E.
∴AE⊥PD.
又BC∩A1B=B,
∴B1E⊥平面A1BCD1,
∴线段B1E的长即为所求.
∵MN⊥AB,AB∥CD,
∴MN⊥CD.
在Rt△A1B1B中,
B1E=,
∴点B1到平面A1BCD1的距离为.
知新探究
【例4】已知在长方体ABCD-A1B1C1D1中,棱AA1=12,AB=5.
⑴求点B1到平面A1BCD1的距离;
⑵求B1C1到平面A1BCD1的距离.
解:
⑵∵B1C1∥BC,且B1C1 平面A1BCD1,BC 平面A1BCD1,
∴B1C1∥平面A1BCD1.
∴点B1到平面A1BCD1的距离即为所求,
∴B1C1到平面A1BCD1的距离为.
初试身手
1.如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a α,a⊥AB.求证:a∥l.
证明:
∵PA⊥α,l α.
∴PA⊥l.
∵PA∩PB=P,PA,PB 平面PAB,
∴a∥l.
又∵PA⊥α,a α,
∴a⊥平面PAB.
同理PB⊥l.
∴PA⊥a.
∵a⊥AB,PA∩AB=A,PA,AB 平面PAB,
∴l⊥平面PAB.
初试身手
2.在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2.
⑴写出点A到平面BCC1B1的距离;
⑵写出直线AB到平面A1B1C1D1的距离;
⑶写出平面ADD1A1与平面BCC1B1之间的距离.
解:
⑵∵AB∥平面A1B1C1D1,
⑴点A到平面BCC1B1的距离h1=AB=4.
⑶∵平面ADD1A1∥平面BCC1B1,
∴AB到平面A1B1C1D1的距离h2=AA1=2.
∴平面ADD1A1与平面BCC1B1之间的距离h3=AB=4.
初试身手
3.如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥平面BCC1B1,F为B1C1的中点.求证:直线A1F∥平面ADE.
证明:
∵CC1⊥平面A1B1C1,且A1F 平面A1B1.
又CC1 平面BCC1B1,B1C1 平面 BCC1B1,CC1∩B1C1=C1,
又AD⊥平面BCC1B1,
∵A1B1=A1C1,F为B1C1的中点,
∴A1F∥AD.
∴A1F∥平面ADE.
∴A1F⊥B1C1,
∴CC1⊥A1F.
∴A1F⊥平面BCC1B1.
又AD 平面ADE,A1F 平面ADE,
课堂小结
1.直线与平面垂直的性质定理
定理 垂直于同一个平面的两条直线平行.
符号语言表示
a⊥α, b⊥α a//b.
图形语言表示
线面垂直 线线平行
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
2.直线到平面的距离、平面到平面的距离
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
作业布置
作业: P155 练习 第2,3, 4题
P164-165 习题8.6 第12, 19,20题
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第七章
8.6.2 直线与平面垂直(第2课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.理解直线与平面垂直的性质定理,并会用直线与平面垂直的性质定理证明相关问题; 1.几何直观素养和逻辑推理素养.
2.理解直线到平面的距离、两个平面间的距离的概念,并会求直线到平面的距离. 2.空间想象素养和逻辑推理素养.
温故知新
1.直线与平面垂直的定义
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.
2.直线与平面垂直的判定定理
定理 如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
用符号语言表示
l⊥m,l⊥n,m α,n α,m∩n=P l⊥α.
图形语言表示
α
P
l
m
n
如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面.
3.点到平面的距离
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段.垂线段的长度叫做点到该平面的距离.
新知引入
观察下列图片,你能发现什么线、面关系的规律吗?
下面我们研究直线与平面垂直的性质,即探究在直线a与平面α垂直的条件下能推出哪些结论.
根据已有经验,我们可以探究直线a与平面α内的直线关系. 但由定义, a与α内的所有直线垂直. 所以,可以探究a , α与其他直线或平面的关系.
我们知道,在平面内,垂直于同一条直线的两条直线平行 . 在空间中是否有类似的性质呢?
新知引入
(1)如图1,在长方体ABCD-A′B′C′D′中,棱AA′、BB′ 、 CC′ 、DD′所在直线都垂直于平面ABCD,它们之间具有什么位置关系
(2)如图2,已知直线a、b和平面α . 如果a⊥α, b⊥α,那么直线a、 b一定平行吗
可以发现 , 这些直线相互平行 . 不失一般性,我们以(2)为例加以证明.
新知探究
如图,假设a与b不平行,且b∩α=O.
显然点O不在直线a上,所以点O与直线a可确定一个平面.
在该平面内过点O作直线b′//a, 则直线b与b'是相交于点O的两条不同直线,所以直线b与b'可确定平面β.
设α∩β=c, 则O∈c.
因为a⊥α, b⊥α,所以a⊥c, b⊥c.
又因为b′//a , 所以b'⊥c.
这样在平面β内,经过直线c上同一点O就有两条直线b、b′与c垂直,显然不可能.
因此 b//a.
由于无法把两条直线a、b归入到一个平面内,所以在定理的证明中,无法应用平面直线的判定知识,也无法应用基本事实4,在这种情况下我们采用了“反证法”.
a
b
α
O
b′
c
β
新知探究
这样,我们得到了直线与平面垂直的一条性质定理.
定理 垂直于同一个平面的两条直线平行.
符号语言表示
a⊥α, b⊥α a//b.
图形语言表示
作用:判断线线平行
线面垂直 线线平行
直线与平面垂直的性质定理告诉我们 , 可以由两条直线与一个平面垂直判定两条直线平行.直线与平面垂直的性质定理揭示了“平行”与“垂直”之间的内在联系.
新知探究
在a⊥α的条件下,如果平面α外的直线b与直线a垂直,你能得到什么结论 如果平面α与平面β平行,你又能得到什么结论
b
a
a⊥α,b⊥a,b α b//α.
a
a⊥α,α//β a⊥β.
α
β
a
在a⊥α的条件下,如果a⊥β,又能得到什么结论?
a⊥α,a⊥β α//β.
知新探究
【例1】如图,直线l平行于平面α,求证:直线l上各点到平面α的距离相等.
证明:
过直线l上任意两点A,B分别作平面α的垂线AA1,BB1,垂足分别为A1,B1.
∴AA1=BB1.
∵ AA1⊥α,BB1⊥α,
∴AA1//BB1.
∵l∥α,
∴l∥A1B1.
设直线AA1,BB1确定的平面为β,β∩α=A1B1,
∴四边形AA1B1B是矩形.
由A,B是直线l上任取的两点,可知直线l上各点到平面α的距离相等.
知新探究
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
a
α
由例1还可以进一步得出,
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
α
β
在棱柱、棱台的体积公式中,它们的高就是它们底面间的距离.
知新探究
【例2】推导棱台体积公式
其中S′,S分别是棱台的上、下底面面积,h是高.
解:
如图,延长棱台各侧棱交于一点P,得到截得棱台的棱锥.过点P作棱台下底面的垂线,分别交棱台的上、下底面于点O′,O,
∴棱台的体积
∴.
.
设截得棱台的棱锥的体积为V,去掉的棱锥的体积为V′,高为h′.则PO′=h′.
则PO垂直于棱台的上底面.从而O′O=h.
知新探究
【例2】推导棱台体积公式
其中S′,S分别是棱台的上、下底面面积,h是高.
解:
.
,
由棱台的上、下底面平行,棱台的上、下底面相似,并且
.
∴.
知新探究
【例3】如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.
证明:AE∥MN.
证明:
∵AD=AP,E是PD的中点,
∴AE⊥AB,
∵AB⊥平面PAD,AE 平面PAD,
又AB∥CD,
∴AE⊥PD.
∴AE⊥CD.
又CD∩PD=D,CD,PD 平面PCD,
∴AE⊥平面PCD.
∵MN⊥AB,AB∥CD,
∴MN⊥CD.
又∵MN⊥PC,PC∩CD=C,PC,CD 平面PCD,
∴MN⊥平面PCD,
∴AE∥MN.
知新探究
【例4】已知在长方体ABCD-A1B1C1D1中,棱AA1=12,AB=5.
⑴求点B1到平面A1BCD1的距离;
⑵求B1C1到平面A1BCD1的距离.
解:
∵AD=AP,E是PD的中点,
⑴如图,过点B1作B1E⊥A1B于点E.
由题意知BC⊥平面A1ABB1,且B1E 平面A1ABB1,
∴BC⊥B1E.
∴AE⊥PD.
又BC∩A1B=B,
∴B1E⊥平面A1BCD1,
∴线段B1E的长即为所求.
∵MN⊥AB,AB∥CD,
∴MN⊥CD.
在Rt△A1B1B中,
B1E=,
∴点B1到平面A1BCD1的距离为.
知新探究
【例4】已知在长方体ABCD-A1B1C1D1中,棱AA1=12,AB=5.
⑴求点B1到平面A1BCD1的距离;
⑵求B1C1到平面A1BCD1的距离.
解:
⑵∵B1C1∥BC,且B1C1 平面A1BCD1,BC 平面A1BCD1,
∴B1C1∥平面A1BCD1.
∴点B1到平面A1BCD1的距离即为所求,
∴B1C1到平面A1BCD1的距离为.
初试身手
1.如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a α,a⊥AB.求证:a∥l.
证明:
∵PA⊥α,l α.
∴PA⊥l.
∵PA∩PB=P,PA,PB 平面PAB,
∴a∥l.
又∵PA⊥α,a α,
∴a⊥平面PAB.
同理PB⊥l.
∴PA⊥a.
∵a⊥AB,PA∩AB=A,PA,AB 平面PAB,
∴l⊥平面PAB.
初试身手
2.在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2.
⑴写出点A到平面BCC1B1的距离;
⑵写出直线AB到平面A1B1C1D1的距离;
⑶写出平面ADD1A1与平面BCC1B1之间的距离.
解:
⑵∵AB∥平面A1B1C1D1,
⑴点A到平面BCC1B1的距离h1=AB=4.
⑶∵平面ADD1A1∥平面BCC1B1,
∴AB到平面A1B1C1D1的距离h2=AA1=2.
∴平面ADD1A1与平面BCC1B1之间的距离h3=AB=4.
初试身手
3.如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥平面BCC1B1,F为B1C1的中点.求证:直线A1F∥平面ADE.
证明:
∵CC1⊥平面A1B1C1,且A1F 平面A1B1.
又CC1 平面BCC1B1,B1C1 平面 BCC1B1,CC1∩B1C1=C1,
又AD⊥平面BCC1B1,
∵A1B1=A1C1,F为B1C1的中点,
∴A1F∥AD.
∴A1F∥平面ADE.
∴A1F⊥B1C1,
∴CC1⊥A1F.
∴A1F⊥平面BCC1B1.
又AD 平面ADE,A1F 平面ADE,
课堂小结
1.直线与平面垂直的性质定理
定理 垂直于同一个平面的两条直线平行.
符号语言表示
a⊥α, b⊥α a//b.
图形语言表示
线面垂直 线线平行
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
2.直线到平面的距离、平面到平面的距离
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
作业布置
作业: P155 练习 第2,3, 4题
P164-165 习题8.6 第12, 19,20题
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
