数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积与体积 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积与体积 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-12 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第八章 立体几何初步
8.3.1 棱柱、棱锥、棱台的表面积与体积
教学目标
了解棱柱、棱锥、棱台的表面积和体积的计算公式;(重点)
01
能用上述公式求棱柱、棱锥、棱台的体积和表面积; (重点、难点)
02
能运
03
04
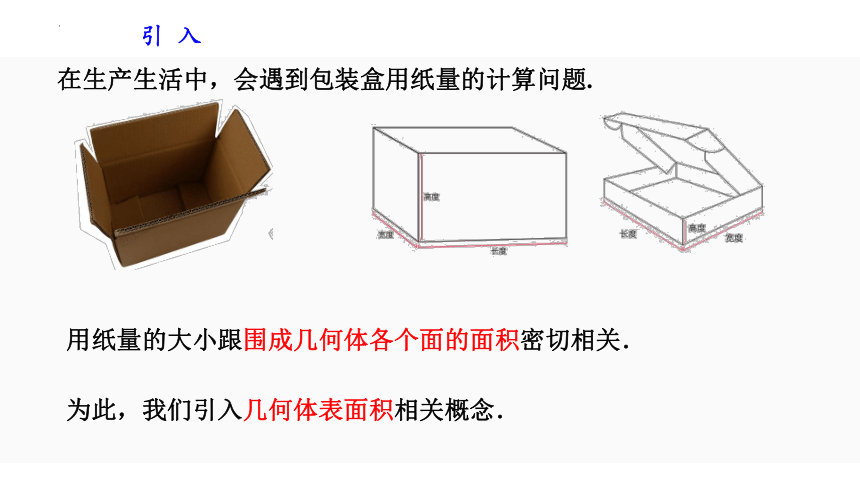
引 入
用纸量的大小跟围成几何体各个面的面积密切相关.
为此,我们引入几何体表面积相关概念.
在生产生活中,会遇到包装盒用纸量的计算问题.
前面我们分别认识了基本立体图形的结构特征和平面表示,本节课进一步学习简单几何体的表面积和体积.表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小.
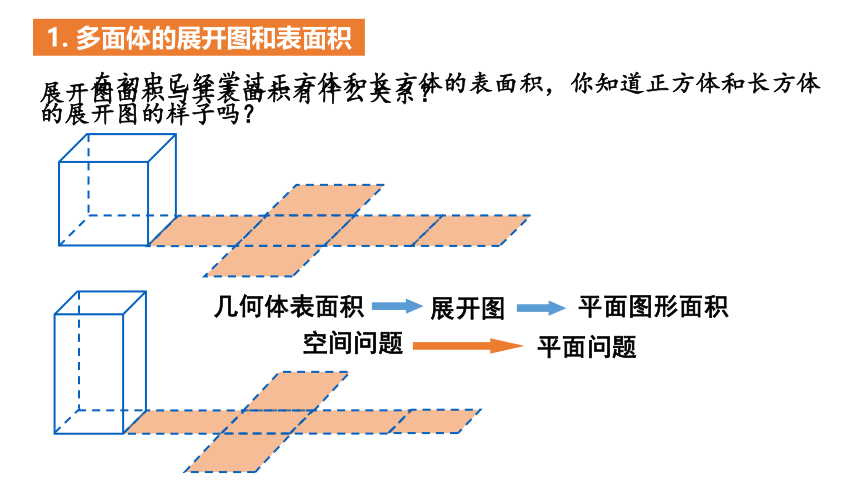
在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图的样子吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
1. 多面体的展开图和表面积
展开图面积与其表面积有什么关系?
新知探究
多面体的表面积就是围成多面体各个面的面积的和.
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和,
也就是展开图的面积.
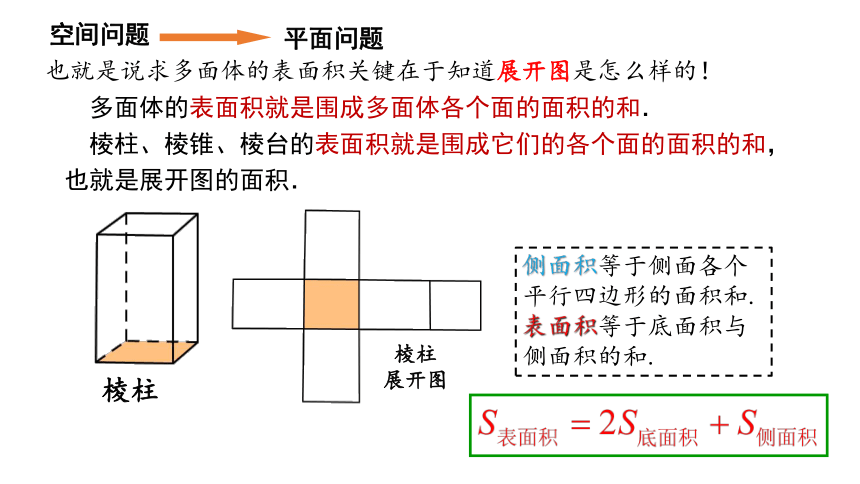
棱柱
棱柱
展开图
侧面积等于侧面各个平行四边形的面积和.
表面积等于底面积与侧面积的和.
空间问题
平面问题
也就是说求多面体的表面积关键在于知道展开图是怎么样的!
新知探究
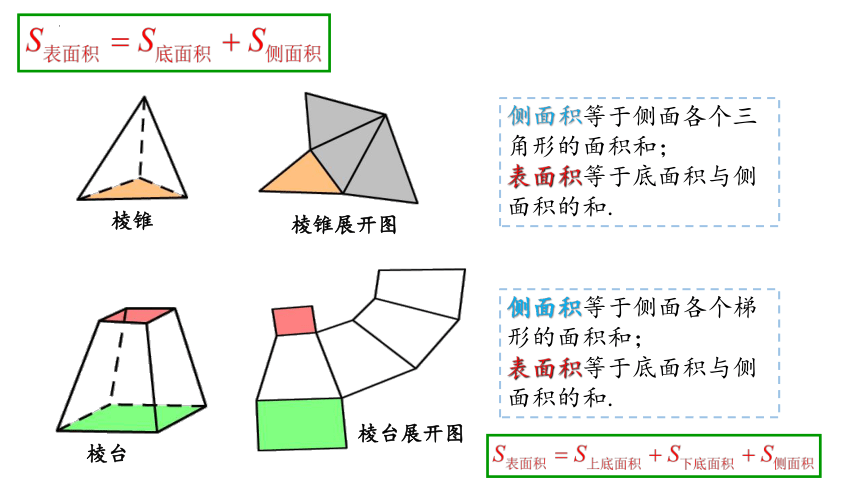
棱锥
侧面积等于侧面各个三角形的面积和;
表面积等于底面积与侧面积的和.
棱锥展开图
棱台
侧面积等于侧面各个梯形的面积和;
表面积等于底面积与侧面积的和.
棱台展开图
【例1】已知棱长为a,各面均为等边三角形的四面体P-ABC,求它的表面积.
B
C
A
P
【解析】因为△PBC是正三角形,其边长为a,
所以
因此,四面体P-ABC的表面积
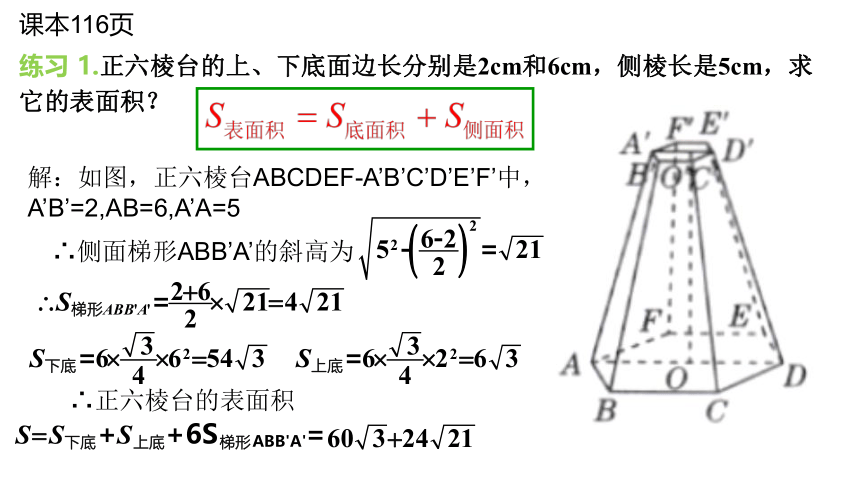
练习 1.正六棱台的上、下底面边长分别是2cm和6cm,侧棱长是5cm,求它的表面积?
解:如图,正六棱台ABCDEF-A’B’C’D’E’F’中,A’B’=2,AB=6,A’A=5
∴侧面梯形ABB’A’的斜高为
∴正六棱台的表面积
课本116页
还记得以前学过的特殊棱柱——正方体、长方体的体积公式吗?
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
2. 多面体的体积
探究新知
①棱柱的体积公式
V棱柱=Sh
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积
棱柱的高是指两底面之间的距离,即从一底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
特别的,直棱柱的侧棱垂直于底面,故侧棱长即为直棱柱的高.
探究新知
探究棱锥与同底等高的棱柱体积之间的关系:
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
探究新知
②棱锥的体积公式
一般地,如果棱锥的底面面积为S,高为h,那么这个棱锥的体积
注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以求点到面的距离.
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
——等体积法
问题:棱台的体积又应该是怎样的呢?
探究新知
探究新知
③棱台的体积公式
由于棱台是由棱锥截成的,因此可以利用两个棱锥的体积差,得到棱台的体积公式
(S′, S, h分别是棱台的上下底面积和高)
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
问题 棱柱、棱锥、棱台的体积公式之间有什么关系?你用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
探究新知
几何体 棱柱 棱台 棱锥
直 观 图
体 积
S’=S
上底扩大
S’=0
上底缩小
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是1.5 m,公共面ABCD是边长为2 m的正方形,那么这个漏斗的容积是多少立方米?
解:
1.某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的.如果被截正方体的棱长是50cm,那么石凳的体积是多少?
课本116页
多面体的表面积就是围成多面体_________的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的_________的面积的和.
1. 棱柱、棱锥、棱台的表面积
各个面
各个面
课堂小结
2. 棱柱、棱锥、棱台的体积
底面积
高
底面积
高
上、下底面面积
高
第八章 立体几何初步
8.3.1 棱柱、棱锥、棱台的表面积与体积
教学目标
了解棱柱、棱锥、棱台的表面积和体积的计算公式;(重点)
01
能用上述公式求棱柱、棱锥、棱台的体积和表面积; (重点、难点)
02
能运
03
04
引 入
用纸量的大小跟围成几何体各个面的面积密切相关.
为此,我们引入几何体表面积相关概念.
在生产生活中,会遇到包装盒用纸量的计算问题.
前面我们分别认识了基本立体图形的结构特征和平面表示,本节课进一步学习简单几何体的表面积和体积.表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小.
在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图的样子吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
1. 多面体的展开图和表面积
展开图面积与其表面积有什么关系?
新知探究
多面体的表面积就是围成多面体各个面的面积的和.
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和,
也就是展开图的面积.
棱柱
棱柱
展开图
侧面积等于侧面各个平行四边形的面积和.
表面积等于底面积与侧面积的和.
空间问题
平面问题
也就是说求多面体的表面积关键在于知道展开图是怎么样的!
新知探究
棱锥
侧面积等于侧面各个三角形的面积和;
表面积等于底面积与侧面积的和.
棱锥展开图
棱台
侧面积等于侧面各个梯形的面积和;
表面积等于底面积与侧面积的和.
棱台展开图
【例1】已知棱长为a,各面均为等边三角形的四面体P-ABC,求它的表面积.
B
C
A
P
【解析】因为△PBC是正三角形,其边长为a,
所以
因此,四面体P-ABC的表面积
练习 1.正六棱台的上、下底面边长分别是2cm和6cm,侧棱长是5cm,求它的表面积?
解:如图,正六棱台ABCDEF-A’B’C’D’E’F’中,A’B’=2,AB=6,A’A=5
∴侧面梯形ABB’A’的斜高为
∴正六棱台的表面积
课本116页
还记得以前学过的特殊棱柱——正方体、长方体的体积公式吗?
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
2. 多面体的体积
探究新知
①棱柱的体积公式
V棱柱=Sh
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积
棱柱的高是指两底面之间的距离,即从一底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
特别的,直棱柱的侧棱垂直于底面,故侧棱长即为直棱柱的高.
探究新知
探究棱锥与同底等高的棱柱体积之间的关系:
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
探究新知
②棱锥的体积公式
一般地,如果棱锥的底面面积为S,高为h,那么这个棱锥的体积
注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以求点到面的距离.
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
——等体积法
问题:棱台的体积又应该是怎样的呢?
探究新知
探究新知
③棱台的体积公式
由于棱台是由棱锥截成的,因此可以利用两个棱锥的体积差,得到棱台的体积公式
(S′, S, h分别是棱台的上下底面积和高)
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
问题 棱柱、棱锥、棱台的体积公式之间有什么关系?你用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
探究新知
几何体 棱柱 棱台 棱锥
直 观 图
体 积
S’=S
上底扩大
S’=0
上底缩小
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是1.5 m,公共面ABCD是边长为2 m的正方形,那么这个漏斗的容积是多少立方米?
解:
1.某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的.如果被截正方体的棱长是50cm,那么石凳的体积是多少?
课本116页
多面体的表面积就是围成多面体_________的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的_________的面积的和.
1. 棱柱、棱锥、棱台的表面积
各个面
各个面
课堂小结
2. 棱柱、棱锥、棱台的体积
底面积
高
底面积
高
上、下底面面积
高
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
