12.2.1-三角形全等的判定SSS
文档属性
| 名称 | 12.2.1-三角形全等的判定SSS |  | |
| 格式 | zip | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-20 22:42:18 | ||
图片预览




文档简介
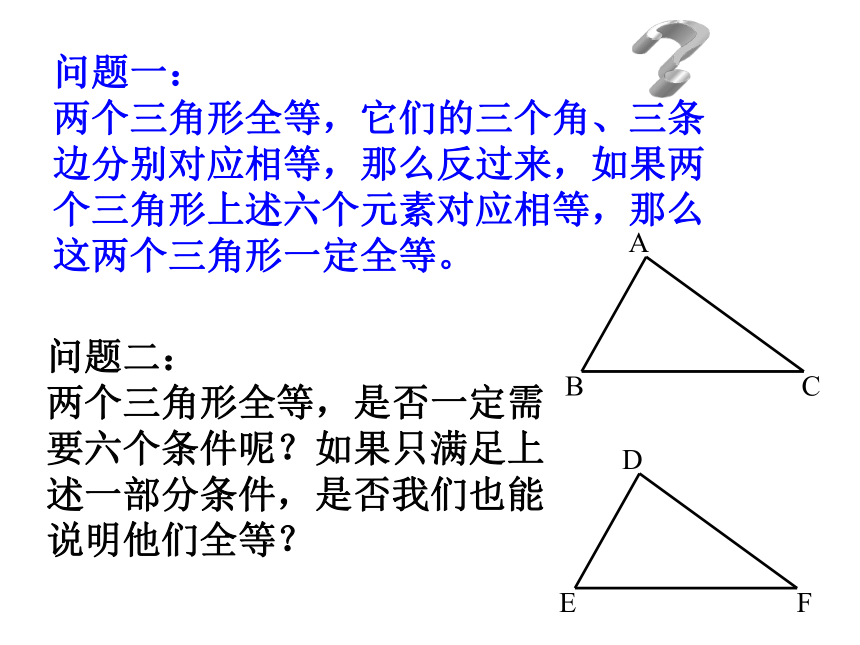
课件27张PPT。知识回顾①AB=DE ② BC=EF ③ AC=DF ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 全等三角形有什么性质?问题一:
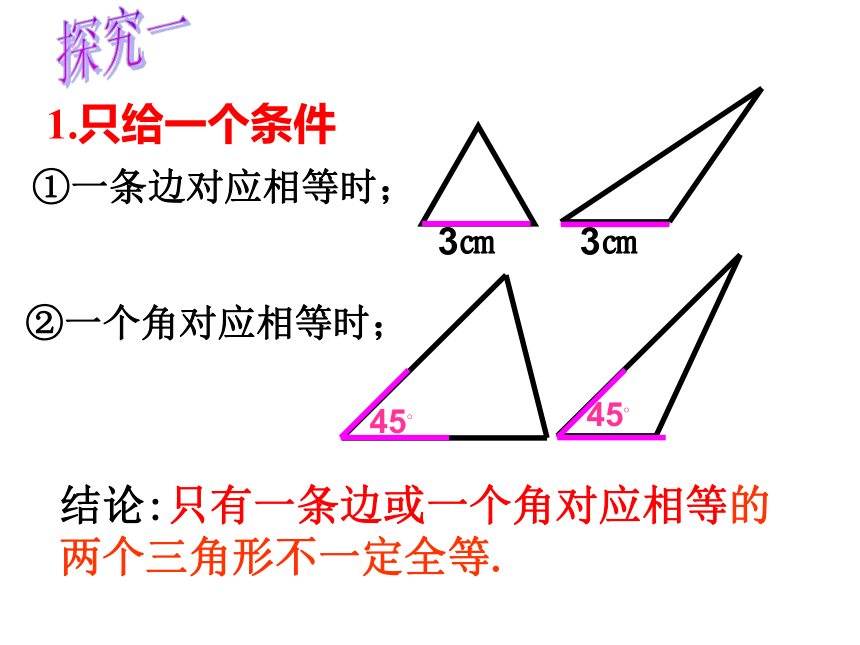
两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形上述六个元素对应相等,那么这两个三角形一定全等。?问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?12.2.1 三角形全等的判定(一) 教学目标:
1、掌握‘‘边边边’’判定三角形全等的方法
2、利用三角形全等的判定方法解决较为 简单的问题
3、提高推理能力,初步形成逻辑思维①一条边对应相等时;3㎝3㎝1.只给一个条件45?②一个角对应相等时;45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.探究一①两条边对应相等;③两个角对应相等。②一条边对应相等和一个角对应相等;2.如果满足两个条件,你能说出有哪几种可能的情况?一角及邻边;
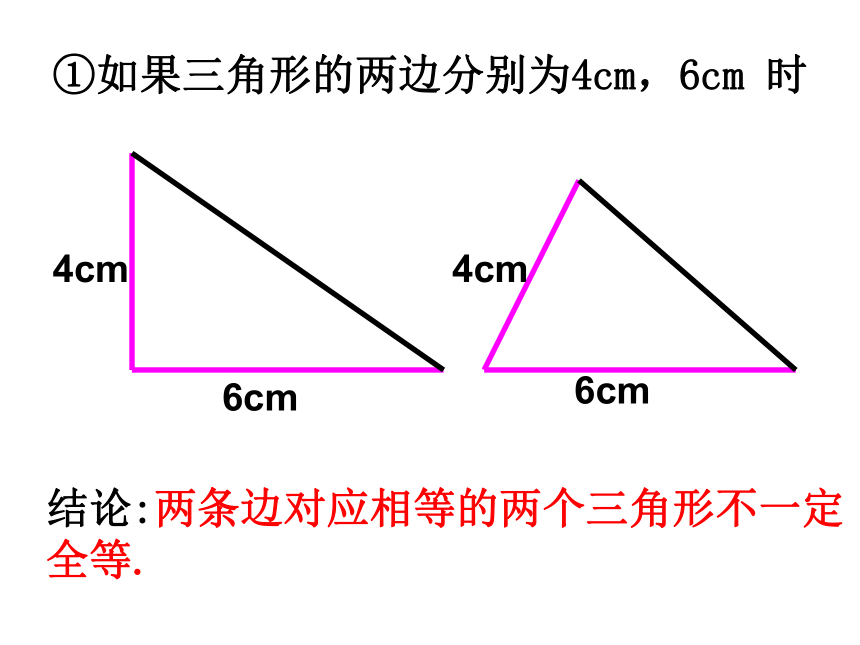
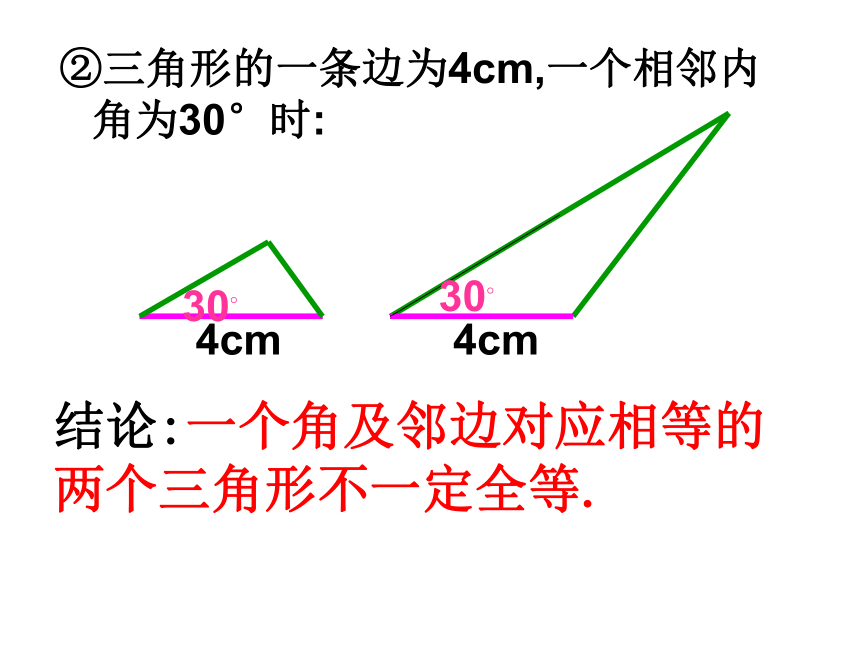
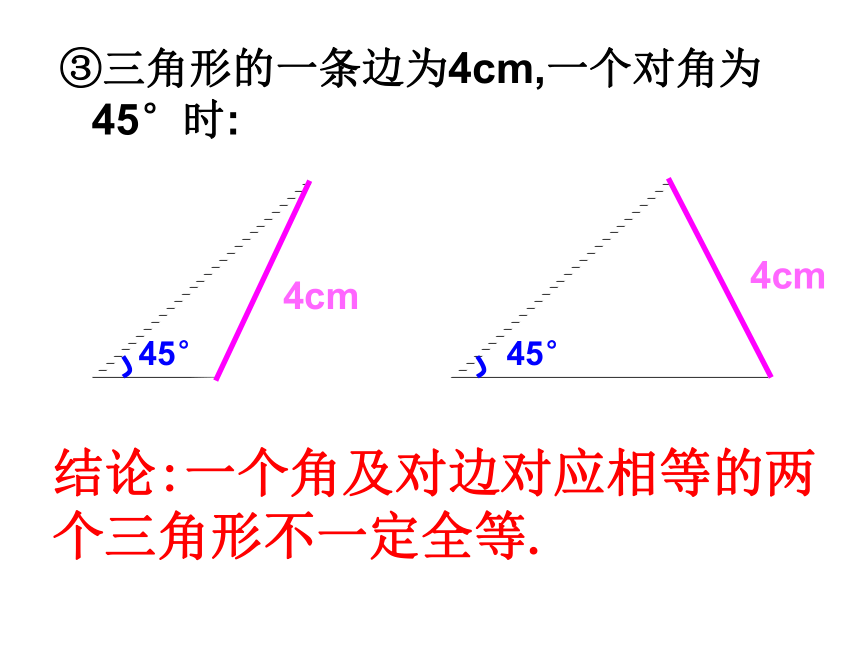
一角及对边①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.②三角形的一条边为4cm,一个相邻内角为30°时:4cm4cm30?30?结论:一个角及邻边对应相等的两个三角形不一定全等.结论:一个角及对边对应相等的两个三角形不一定全等.45°45°4cm4cm③三角形的一条边为4cm,一个对角为45°时:④如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.两个条件
①两角;
②两边;
③一角一边
一角及邻边;
一角及对边;结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?④三个角.①三条边;②两边一角;③两角一边; 3.如果满足三个条件,你能说出有哪几种可能的情况?探索三角形全等的条件 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定全等。探究活动3、三个条件结论已知两个三角形的三条边都分别为3cm、4cm、6cm 。它们一定全等吗?①三条边 2、已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?三边对应相等的两个三角形全等,探究新知先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’剪下,放到△ABC上,他们全等吗?画法:
1.画线段 B’C’ =BC;2.分别以 B’ , C’为圆心,BA, CA为半径画弧,
两弧交于点A’;3. 连接线段 A’B’ , A’C’ .探究上述结论反映了什么规律? 三边对应相等的两个三角形全等。
简写为“边边边”或“SSS”
边边边公理: 注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形稳定性的原理。 在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS) 判断两个三角形全等的推理过程,叫做证明三角形全等。
如何用符号语言来表达呢? A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD求证:∠B=∠C,∴∠B=∠C,归纳:①准备条件:证全等时要用的条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用半个大括号括起来写出全等结论证明三角形全等的书写步骤:BCCB△DCBBF=CD或 BD=CF
例2 如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA
(2)∠B=∠DABCD1.已知:AC=AD,BC=BD,
求证:(1)△ABC≌ △ABD
(2)AB是∠DAC的平分线. ∵ AC=AD( )BC=BD( )AB=AB( )∴△ABC≌△ABD( )(2)∵△ ABC≌△ABD ∴∠1=∠2∴AB是∠DAC的平分线(全等三角形的对应角相等)已知已知公共边SSS(角平分线定义)证明:(1)在△ABC和△ABD中练习作图——作一个角等于已知角 作法:1.以点O为圆心,任意长为半径作弧,分别交OA、OB于点C、D;
2.画一条射线O1A1,以点O1为圆心,OC长为半径画弧,交O1A1于点C1;
3.以点C1为圆心,CD长为半径画弧,与上弧交于点D1;
4.过点D1画射线O1B1,则∠A1O1B1=∠AOBABO已知:∠AOB 求作:∠A1O1B1,使得∠A1O1B1=∠AOB图1提高练习:
1、已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD
即 AB=FD(等式性质)
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)求证:∠C=∠E .==??。。∴ ∠C=∠E (全等三角形的对应角相等) 求证:AC∥EF;DE∥BC
2、已知:如图,AB=AC,DB=DC,
请说明∠B =∠C成立的理由ABCD3、已知: 如图, 四边形ABCD中,AD=CB,AB=CD
求证: ∠A= ∠C。A C D B构造公共边是常添的辅助线1.边边边公理:有三边对应相等的两个三角形全等,简写成“边边边”(SSS)2.边边边公理在应用中用到的数学方法:
证明线段(或角)相等 转 化 证明线段(或角)所在的两个三角形全等.证明两个三角形全等的注意点:(1)两三角形全等所需的条件应按对应的顺序书写.
(2)小结:有时需添辅助线(如:构造公共边)
两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形上述六个元素对应相等,那么这两个三角形一定全等。?问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?12.2.1 三角形全等的判定(一) 教学目标:
1、掌握‘‘边边边’’判定三角形全等的方法
2、利用三角形全等的判定方法解决较为 简单的问题
3、提高推理能力,初步形成逻辑思维①一条边对应相等时;3㎝3㎝1.只给一个条件45?②一个角对应相等时;45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.探究一①两条边对应相等;③两个角对应相等。②一条边对应相等和一个角对应相等;2.如果满足两个条件,你能说出有哪几种可能的情况?一角及邻边;
一角及对边①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.②三角形的一条边为4cm,一个相邻内角为30°时:4cm4cm30?30?结论:一个角及邻边对应相等的两个三角形不一定全等.结论:一个角及对边对应相等的两个三角形不一定全等.45°45°4cm4cm③三角形的一条边为4cm,一个对角为45°时:④如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.两个条件
①两角;
②两边;
③一角一边
一角及邻边;
一角及对边;结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?④三个角.①三条边;②两边一角;③两角一边; 3.如果满足三个条件,你能说出有哪几种可能的情况?探索三角形全等的条件 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定全等。探究活动3、三个条件结论已知两个三角形的三条边都分别为3cm、4cm、6cm 。它们一定全等吗?①三条边 2、已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?三边对应相等的两个三角形全等,探究新知先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’剪下,放到△ABC上,他们全等吗?画法:
1.画线段 B’C’ =BC;2.分别以 B’ , C’为圆心,BA, CA为半径画弧,
两弧交于点A’;3. 连接线段 A’B’ , A’C’ .探究上述结论反映了什么规律? 三边对应相等的两个三角形全等。
简写为“边边边”或“SSS”
边边边公理: 注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形稳定性的原理。 在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS) 判断两个三角形全等的推理过程,叫做证明三角形全等。
如何用符号语言来表达呢? A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD求证:∠B=∠C,∴∠B=∠C,归纳:①准备条件:证全等时要用的条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用半个大括号括起来写出全等结论证明三角形全等的书写步骤:BCCB△DCBBF=CD或 BD=CF
例2 如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA
(2)∠B=∠DABCD1.已知:AC=AD,BC=BD,
求证:(1)△ABC≌ △ABD
(2)AB是∠DAC的平分线. ∵ AC=AD( )BC=BD( )AB=AB( )∴△ABC≌△ABD( )(2)∵△ ABC≌△ABD ∴∠1=∠2∴AB是∠DAC的平分线(全等三角形的对应角相等)已知已知公共边SSS(角平分线定义)证明:(1)在△ABC和△ABD中练习作图——作一个角等于已知角 作法:1.以点O为圆心,任意长为半径作弧,分别交OA、OB于点C、D;
2.画一条射线O1A1,以点O1为圆心,OC长为半径画弧,交O1A1于点C1;
3.以点C1为圆心,CD长为半径画弧,与上弧交于点D1;
4.过点D1画射线O1B1,则∠A1O1B1=∠AOBABO已知:∠AOB 求作:∠A1O1B1,使得∠A1O1B1=∠AOB图1提高练习:
1、已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD
即 AB=FD(等式性质)
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)求证:∠C=∠E .==??。。∴ ∠C=∠E (全等三角形的对应角相等) 求证:AC∥EF;DE∥BC
2、已知:如图,AB=AC,DB=DC,
请说明∠B =∠C成立的理由ABCD3、已知: 如图, 四边形ABCD中,AD=CB,AB=CD
求证: ∠A= ∠C。A C D B构造公共边是常添的辅助线1.边边边公理:有三边对应相等的两个三角形全等,简写成“边边边”(SSS)2.边边边公理在应用中用到的数学方法:
证明线段(或角)相等 转 化 证明线段(或角)所在的两个三角形全等.证明两个三角形全等的注意点:(1)两三角形全等所需的条件应按对应的顺序书写.
(2)小结:有时需添辅助线(如:构造公共边)
