人教A必修2(浙江省台州市椒江区)
文档属性
| 名称 | 人教A必修2(浙江省台州市椒江区) |

|
|
| 格式 | rar | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-13 00:00:00 | ||
图片预览




文档简介
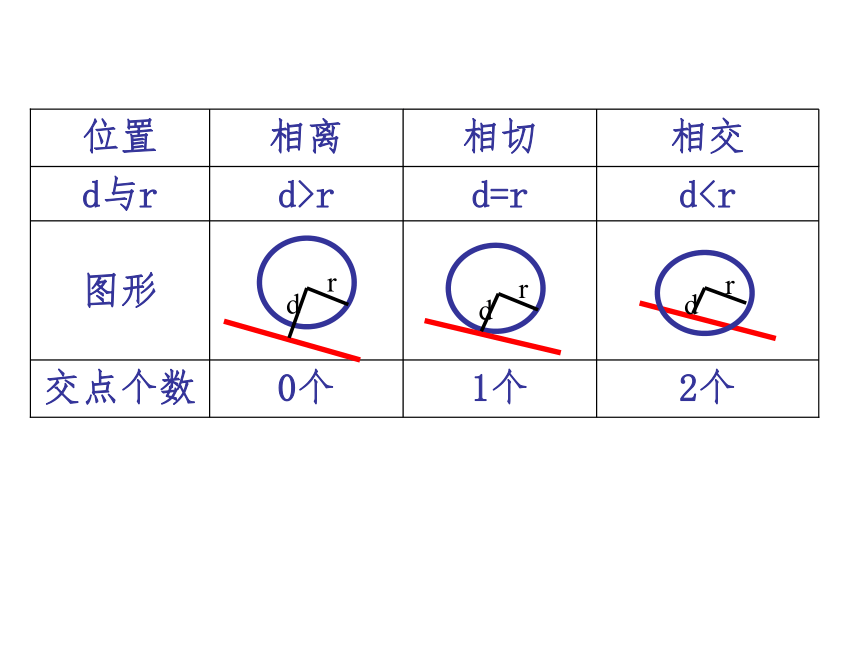
课件18张PPT。复习回顾:直线与圆的位置关系:相离、相交、相切判断直线与圆的位置关系有哪些方法?(1)根据圆心到直线的距离;(2)根据直线的方程和圆的方程组成方程组的实数解的个数; 直线与圆的位置关系: 法一(判别式法):直线Ax + By + C = 0;圆x2 + y2 + Dx + Ey + F = 0. 一元二次方程 注:为使消元更方便,这里使用圆的一般方程. 法二(几何法):直线:Ax + By + C = 0;
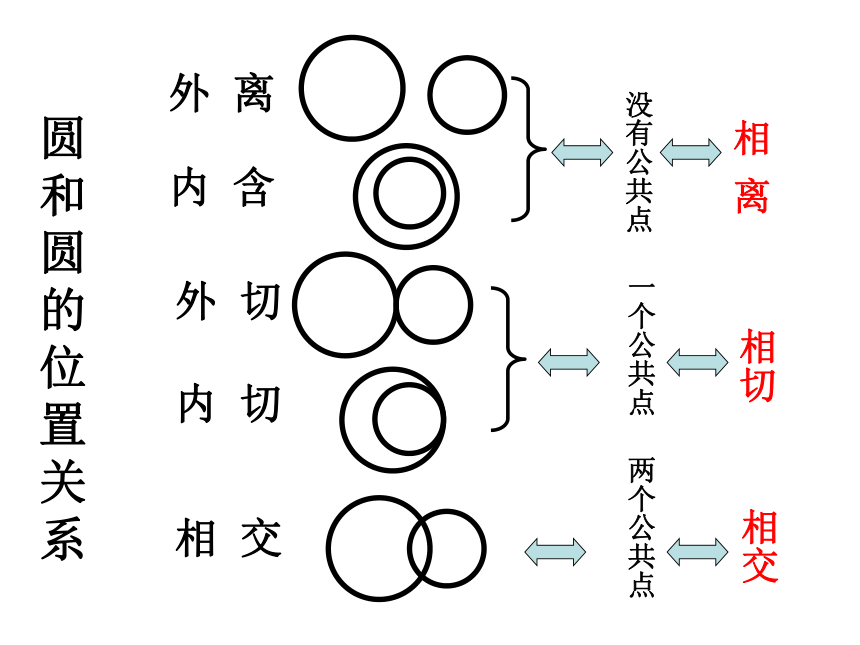
圆:(x ? a)2 + ( y ? b)2 = r2,则 注:为使求圆心到直线的距离更方便,这里使用圆的标准方程.综上, 在解析几何中, 直线与圆的位置关系完全可由相应的数量关系来刻划.§4.2.2 圆与圆的位置关系圆与圆的位置关系:相离、外切、相交、内切、内含圆
和
圆
的
位
置
关
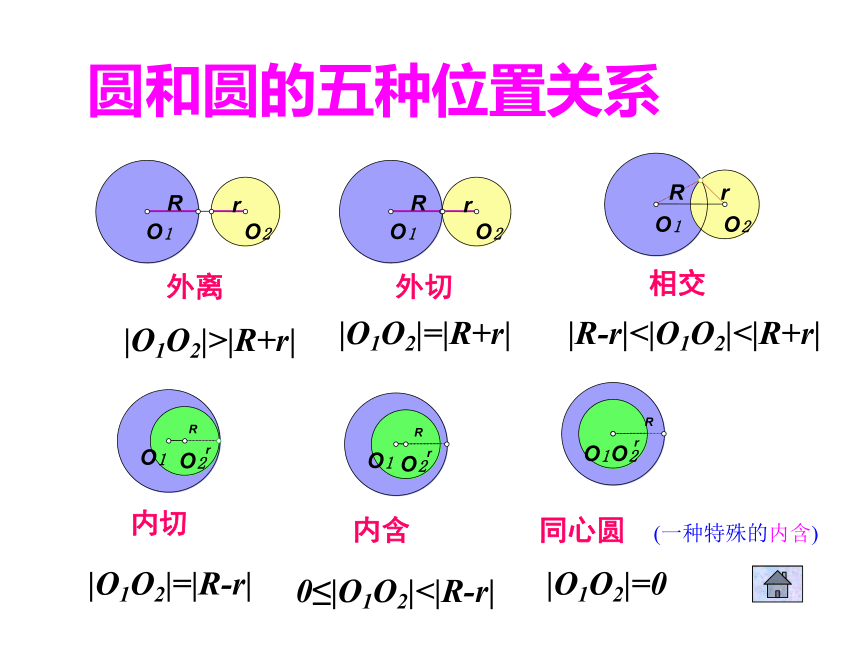
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交外离圆和圆的五种位置关系|O1O2|>|R+r||O1O2|=|R+r||R-r|<|O1O2|<|R+r||O1O2|=|R-r|0≤|O1O2|<|R-r||O1O2|=0外切相交内切内含同心圆(一种特殊的内含)圆与圆的位置关系
设圆O1的半径为r1,圆O2的半径为r2,
则两圆相离? |O1O2|>r1+r2,
两圆外切? |O1O2|=r1+r2,
两圆相交? |r1-r2|<|O1O2|<|r1+r2|
两圆内切? |O1O2|=|r1-r2|,
两圆内含? |O1O2|<|r1-r2|, (1)利用连心线长与|r1+r2|和| r1-r2 |的大小关系判断:(2) 利用两个圆的方程组成方程组的实数解的个数:练习1⊙01和⊙ 02 的半径分别为3cm 和 4 cm ,设
(1) 0102= 8cm (2) 0102 = 7cm
(3) 0102 =5cm (4) 0102 = 1cm
(5) 0102=0.5cm (6) 01和02重合
⊙01和⊙02的位置关系怎样? (2)两圆外切(3)两圆相交 (4)两圆内切 (5)两圆内含 (6)两圆同心答: (1)两圆相离练习2. 若两圆x2+y2=9与x2+y2-4ax-2y+4a2-3=0
相切,求实数a的值.两圆相切可能是内切也可能是外切即d=R+r或d=|R-r|解法一:把圆C1和圆C2的方程化为标准方程:例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.所以圆C1与圆C2相交,它们有两个公共点A,B.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.解法二:圆C1与圆C2的方程联立,得(1)-(2),得所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1, y2. 因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.练习
点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求 |MN| 的最大值.解:把圆的方程都化成标准形式,为
(x+3)2+(y-1)2=9
(x+1)2+(y+2)2=4
如图,C1的坐标是(-3,1),半径是3;C2的坐标是(-1,-2),半径是2,所以,
|C1C2|= =
因此,|MN|的最大值是 +5.
练:已知圆C:x2+y2-2x+4y-4=0,问:
是否存在斜率为1的直线使l被圆C截得
得弦AB为直径的圆过原点,若存在,
写出直线方程
圆:(x ? a)2 + ( y ? b)2 = r2,则 注:为使求圆心到直线的距离更方便,这里使用圆的标准方程.综上, 在解析几何中, 直线与圆的位置关系完全可由相应的数量关系来刻划.§4.2.2 圆与圆的位置关系圆与圆的位置关系:相离、外切、相交、内切、内含圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交外离圆和圆的五种位置关系|O1O2|>|R+r||O1O2|=|R+r||R-r|<|O1O2|<|R+r||O1O2|=|R-r|0≤|O1O2|<|R-r||O1O2|=0外切相交内切内含同心圆(一种特殊的内含)圆与圆的位置关系
设圆O1的半径为r1,圆O2的半径为r2,
则两圆相离? |O1O2|>r1+r2,
两圆外切? |O1O2|=r1+r2,
两圆相交? |r1-r2|<|O1O2|<|r1+r2|
两圆内切? |O1O2|=|r1-r2|,
两圆内含? |O1O2|<|r1-r2|, (1)利用连心线长与|r1+r2|和| r1-r2 |的大小关系判断:(2) 利用两个圆的方程组成方程组的实数解的个数:练习1⊙01和⊙ 02 的半径分别为3cm 和 4 cm ,设
(1) 0102= 8cm (2) 0102 = 7cm
(3) 0102 =5cm (4) 0102 = 1cm
(5) 0102=0.5cm (6) 01和02重合
⊙01和⊙02的位置关系怎样? (2)两圆外切(3)两圆相交 (4)两圆内切 (5)两圆内含 (6)两圆同心答: (1)两圆相离练习2. 若两圆x2+y2=9与x2+y2-4ax-2y+4a2-3=0
相切,求实数a的值.两圆相切可能是内切也可能是外切即d=R+r或d=|R-r|解法一:把圆C1和圆C2的方程化为标准方程:例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.所以圆C1与圆C2相交,它们有两个公共点A,B.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.解法二:圆C1与圆C2的方程联立,得(1)-(2),得所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1, y2. 因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.练习
点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求 |MN| 的最大值.解:把圆的方程都化成标准形式,为
(x+3)2+(y-1)2=9
(x+1)2+(y+2)2=4
如图,C1的坐标是(-3,1),半径是3;C2的坐标是(-1,-2),半径是2,所以,
|C1C2|= =
因此,|MN|的最大值是 +5.
练:已知圆C:x2+y2-2x+4y-4=0,问:
是否存在斜率为1的直线使l被圆C截得
得弦AB为直径的圆过原点,若存在,
写出直线方程
