江苏省南通市海门区东洲国际学校2023-2024学年九年级下学期4月月考数学试题(无答案)
文档属性
| 名称 | 江苏省南通市海门区东洲国际学校2023-2024学年九年级下学期4月月考数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 393.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 18:00:43 | ||
图片预览


文档简介
南通海门区东洲国际学校九年级2024学年度4月份第二次月度考试
数学卷
注 意 事 项
考生在答题前请认真阅读本注意事项:
1.本试卷共7页,满分为150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位置.
3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效.
4.作弊者,本卷按0分处理。
班级: 姓名; 学号:
考场号: 座位号:
(请考生将自己信息如实填写在上面,不写、漏写、错写为无效试卷)
选择题(每题3分,共30分)
1.下列各式中结果最小的是( )
A.|﹣4| B.﹣(﹣2) C.﹣(+) D.﹣|﹣7|
2.要使分式有意义,则x的取值范围是( );
A. B. C. D.
3.据国家统计局数据,2021年中国国内生产总值约1 144 000亿元.将1 144 000用科学记数法表示为( )
A.0.1144×107 B.1.144×107 C.0.1144×106 D.1.144×106
4.某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系
5.已知四边形ABCD,下列说法正确的有( );
A. 当AD=BC,AB∥DC时,四边形ABCD是平行四边形;
B. 当AD=BC,AB=DC时,四边形ABCD是平行四边形;
C. 当AC=BD,AC平分BD时,四边形ABCD是矩形;
D. 当AC=BD,AC⊥BD时,四边形ABCD是正方形
6.若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
7.如图,随意向水平放置的大⊙O内部区域抛一个小球,△ABC为正三角形,则小球落在小⊙O内部(阴影)区域的概率为( )
A. B. C. D.
8.已知二次函数,当时,y随x的增大而增大,而m的取值范围是( );
A. B. C. D.
9.如图所示,在Rt△ABC中,∠A=30°,AB=4,点D为边AB的中点,点P为边AC上的动点,则PB+PD的最小值为( )
A. B. C. D.
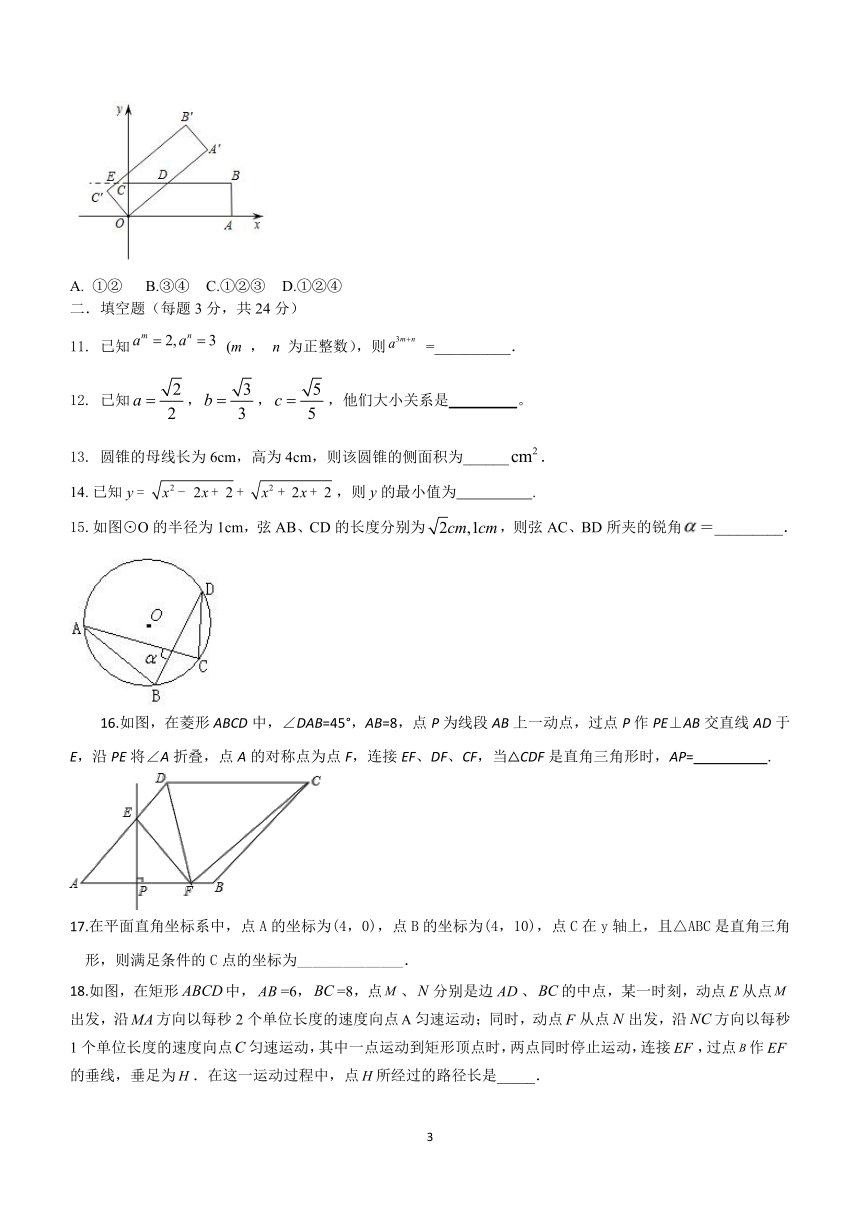
10.如图,在平面直角坐标系中,点O为坐标原点,矩形按如图所示摆放在第一象限,点B的坐标为,将矩形绕着点O逆时针旋转(),得到矩形.直线、与直线相交,交点分别为点D、E,有下列说法:
①当时,矩形与矩形重叠部分的面积为;
②当,且落到y轴的正半轴上时,的长为;
③当点D为线段的中点时,点D的横坐标为;
④当点D是线段的三等分点时,的值为或.
其中,说法正确的是( )
①② B.③④ C.①②③ D.①②④
填空题(每题3分,共24分)
已知 (m , n 为正整数),则 =__________.
已知,,,他们大小关系是 。
圆锥的母线长为6cm,高为4cm,则该圆锥的侧面积为______.
已知,则y的最小值为 .
15.如图⊙O的半径为1cm,弦AB、CD的长度分别为,则弦AC、BD所夹的锐角=_________.
16.如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF是直角三角形时,AP= .
17.在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(4,10),点C在y轴上,且△ABC是直角三角形,则满足条件的C点的坐标为______________.
18.如图,在矩形中,=6,=8,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是_____.
解答题(共96分)
计算(共6分)(1)不等式组的解集
计算:.
20.(10分)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x﹣=0,就可以利用该思维方式,设=y,将原方程转化为:y2﹣y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足,求x2+y2的值.
21.(10分)现有A,B两个不透明的袋子,分别装有3个小球(每个袋中的小球除颜色外,其他完全相同).A袋装有1个白球,2个红球;B袋装有1个红球,2个白球.
1、将A袋摇匀,然后从A袋中随机摸出一个球,则摸出的小球是红球的概率为______;
2、甲、乙两人玩摸球游戏,并设计了如下规则:甲从A袋中随机摸出一个小球,乙从B袋中随机摸出一个小球.若甲、乙两人摸到的小球颜色相同,则甲获胜;若颜色不同,则乙获胜.这个游戏规则公平吗?为什么?(请用画树状图或列表的方法说明理由)
22.(10分)如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,
AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。
23.(12分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元;
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率;
24.(12分)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在,
轴、轴的正半轴上,A(3,0),B(0,4),D为边OB的中点。
(1)若E为边OA上的一个动点,求△CDE的周长最小值;
(2)若E、F为边OA上的两个动点,且EF=1,当四边形CDEF的周长最小时,求点E、F的坐标。
25.(14分)如图,A(a,at-2)、B(b,bt-2)是反比例函数(k≠0)的图象上两点,直线AB与x轴交于点C、与y轴交于点D.
1、求点D坐标;
2、用t的代数式表示a+b;
3、若A(-3,1)
①已知M(x1,y1)、N(x2,y2)(x1<x2) 是线段AB上两点,MN:AB=3:4,且线段MN与双曲线无交点,求x1的取值范围;
②若经过点D的直线y=mx+n与反比例函数的图像分别交于P、Q两点,且△POQ内有横坐标和纵坐标都为整数的点共5个,直接写出m的取值范围.
26.(9分)随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业旅游年消费情况进行了问卷调查,随机抽取部分员工,记录每个人消费金额,并将调查数据适当调整,绘制成如图两幅尚不完整的表和图,根据以下信息回答下列问题:
组别 个人年消费/元 频数/人数 频率
A ≤2000 18
B 2000<≤4000
C 4000<≤6000
D 6000<≤8000 24
E >8000 12
合计
(1)______,______,______;并将条形统计图补充完整;
(2)这次调查中,个人年消费金额的中位数出现在______组;
(3)若这个企业有3000多名员工,请你估计个人旅游年消费金额在6000元以上的约有______人
27.(13分)对某一个函数给出如下定义;当自变量x满足(m,n为实数,)时,函数y有最大值,且最大值为,则称该函数为理想函数.
(1)当,时,在①;②中,______是理想函数;
(2)当时,反比例函数是理想函数,求实数m的值;
(3)已知二次函数是理想函数,且最大值为2m+4.将该函数图象向左平移个单位长度所得图象记为C,,是图象C上两个不同的点.若,求证:.
数学卷
注 意 事 项
考生在答题前请认真阅读本注意事项:
1.本试卷共7页,满分为150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位置.
3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效.
4.作弊者,本卷按0分处理。
班级: 姓名; 学号:
考场号: 座位号:
(请考生将自己信息如实填写在上面,不写、漏写、错写为无效试卷)
选择题(每题3分,共30分)
1.下列各式中结果最小的是( )
A.|﹣4| B.﹣(﹣2) C.﹣(+) D.﹣|﹣7|
2.要使分式有意义,则x的取值范围是( );
A. B. C. D.
3.据国家统计局数据,2021年中国国内生产总值约1 144 000亿元.将1 144 000用科学记数法表示为( )
A.0.1144×107 B.1.144×107 C.0.1144×106 D.1.144×106
4.某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系
5.已知四边形ABCD,下列说法正确的有( );
A. 当AD=BC,AB∥DC时,四边形ABCD是平行四边形;
B. 当AD=BC,AB=DC时,四边形ABCD是平行四边形;
C. 当AC=BD,AC平分BD时,四边形ABCD是矩形;
D. 当AC=BD,AC⊥BD时,四边形ABCD是正方形
6.若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
7.如图,随意向水平放置的大⊙O内部区域抛一个小球,△ABC为正三角形,则小球落在小⊙O内部(阴影)区域的概率为( )
A. B. C. D.
8.已知二次函数,当时,y随x的增大而增大,而m的取值范围是( );
A. B. C. D.
9.如图所示,在Rt△ABC中,∠A=30°,AB=4,点D为边AB的中点,点P为边AC上的动点,则PB+PD的最小值为( )
A. B. C. D.
10.如图,在平面直角坐标系中,点O为坐标原点,矩形按如图所示摆放在第一象限,点B的坐标为,将矩形绕着点O逆时针旋转(),得到矩形.直线、与直线相交,交点分别为点D、E,有下列说法:
①当时,矩形与矩形重叠部分的面积为;
②当,且落到y轴的正半轴上时,的长为;
③当点D为线段的中点时,点D的横坐标为;
④当点D是线段的三等分点时,的值为或.
其中,说法正确的是( )
①② B.③④ C.①②③ D.①②④
填空题(每题3分,共24分)
已知 (m , n 为正整数),则 =__________.
已知,,,他们大小关系是 。
圆锥的母线长为6cm,高为4cm,则该圆锥的侧面积为______.
已知,则y的最小值为 .
15.如图⊙O的半径为1cm,弦AB、CD的长度分别为,则弦AC、BD所夹的锐角=_________.
16.如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF是直角三角形时,AP= .
17.在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(4,10),点C在y轴上,且△ABC是直角三角形,则满足条件的C点的坐标为______________.
18.如图,在矩形中,=6,=8,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是_____.
解答题(共96分)
计算(共6分)(1)不等式组的解集
计算:.
20.(10分)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x﹣=0,就可以利用该思维方式,设=y,将原方程转化为:y2﹣y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足,求x2+y2的值.
21.(10分)现有A,B两个不透明的袋子,分别装有3个小球(每个袋中的小球除颜色外,其他完全相同).A袋装有1个白球,2个红球;B袋装有1个红球,2个白球.
1、将A袋摇匀,然后从A袋中随机摸出一个球,则摸出的小球是红球的概率为______;
2、甲、乙两人玩摸球游戏,并设计了如下规则:甲从A袋中随机摸出一个小球,乙从B袋中随机摸出一个小球.若甲、乙两人摸到的小球颜色相同,则甲获胜;若颜色不同,则乙获胜.这个游戏规则公平吗?为什么?(请用画树状图或列表的方法说明理由)
22.(10分)如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,
AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。
23.(12分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元;
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率;
24.(12分)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在,
轴、轴的正半轴上,A(3,0),B(0,4),D为边OB的中点。
(1)若E为边OA上的一个动点,求△CDE的周长最小值;
(2)若E、F为边OA上的两个动点,且EF=1,当四边形CDEF的周长最小时,求点E、F的坐标。
25.(14分)如图,A(a,at-2)、B(b,bt-2)是反比例函数(k≠0)的图象上两点,直线AB与x轴交于点C、与y轴交于点D.
1、求点D坐标;
2、用t的代数式表示a+b;
3、若A(-3,1)
①已知M(x1,y1)、N(x2,y2)(x1<x2) 是线段AB上两点,MN:AB=3:4,且线段MN与双曲线无交点,求x1的取值范围;
②若经过点D的直线y=mx+n与反比例函数的图像分别交于P、Q两点,且△POQ内有横坐标和纵坐标都为整数的点共5个,直接写出m的取值范围.
26.(9分)随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业旅游年消费情况进行了问卷调查,随机抽取部分员工,记录每个人消费金额,并将调查数据适当调整,绘制成如图两幅尚不完整的表和图,根据以下信息回答下列问题:
组别 个人年消费/元 频数/人数 频率
A ≤2000 18
B 2000<≤4000
C 4000<≤6000
D 6000<≤8000 24
E >8000 12
合计
(1)______,______,______;并将条形统计图补充完整;
(2)这次调查中,个人年消费金额的中位数出现在______组;
(3)若这个企业有3000多名员工,请你估计个人旅游年消费金额在6000元以上的约有______人
27.(13分)对某一个函数给出如下定义;当自变量x满足(m,n为实数,)时,函数y有最大值,且最大值为,则称该函数为理想函数.
(1)当,时,在①;②中,______是理想函数;
(2)当时,反比例函数是理想函数,求实数m的值;
(3)已知二次函数是理想函数,且最大值为2m+4.将该函数图象向左平移个单位长度所得图象记为C,,是图象C上两个不同的点.若,求证:.
同课章节目录
