沪教版(五四制)八年级数学下册试题 20.3.1一次函数与方程不等式 同步练习(含答案)
文档属性
| 名称 | 沪教版(五四制)八年级数学下册试题 20.3.1一次函数与方程不等式 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 21:14:38 | ||
图片预览





文档简介
20.3.1一次函数与方程不等式
一、选择题.
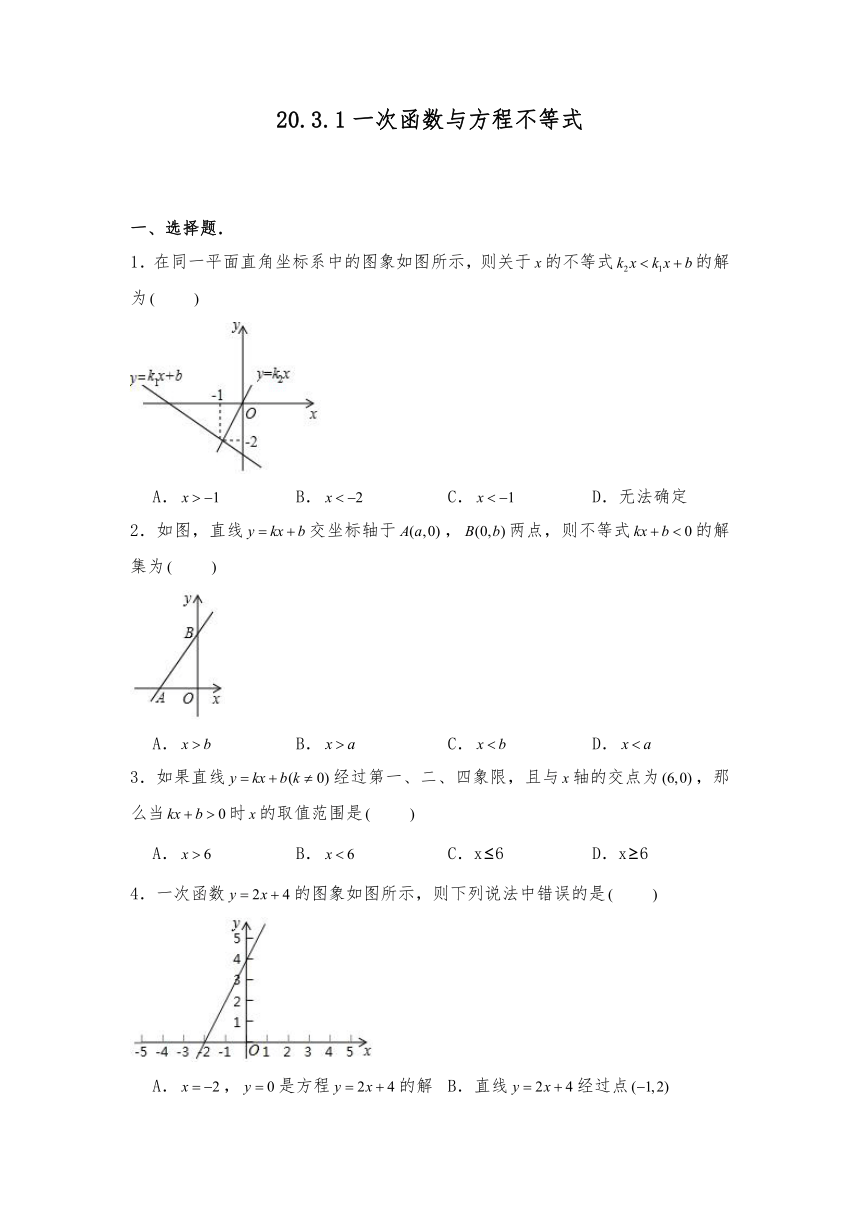
1.在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为
A. B. C. D.无法确定
2.如图,直线交坐标轴于,两点,则不等式的解集为
A. B. C. D.
3.如果直线经过第一、二、四象限,且与轴的交点为,那么当时的取值范围是
A. B. C.x≤6 D.x≥6
4.一次函数的图象如图所示,则下列说法中错误的是
A.,是方程的解 B.直线经过点
C.当时, D.当时,
5.如图,已知函数和图象交于点,点的横坐标为1,则关于,的方程组的解是
A. B. C. D.
6.如图,直线和直线相交于点,根据图象可知,关于的方程的解是
A. B. C.或25 D.
7.如图,已知直线过点,过点的直线交轴于点,则不等式的解集为
A. B. C. D.
8.一次函数与的图象如图所示,下列说法:
①对于函数来说,随的增大而减小
②函数不经过第一象限,
③不等式的解集是,
④,其中正确的个数有
A.4 B.3 C.2 D.1
9.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③不等式的解集是;④.其中正确的个数有
A.4 B.3 C.2 D.1
10.一次函数与的图象如图所示,下列说法:①对于函数来说,随的增大而增大;②函数不经过第二象限;③不等式ax-d≥cx-b的解集是x≥4;④,其中正确的是
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题
11.已知直线和交于点,则关于的方程的解为 .
12.已知直线与相交于点,则关于,的二元一次方程组的解为 .
13.已知二元一次方程组的解为,则在同一平面直角坐标系中,函数与的图象的交点坐标为 .
14.如图,已知直线和直线交于点,则关于、的方程组的解是 .
15.如图,直角坐标系中,直线和直线相交于点,则方程组的解为 .
16.如图,一次函数与正比例函数在同一平面坐标系的图象如图所示,则关于的不等式的解集为 .
17.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)与的交点坐标.据此,则矩阵式所对应两直线交点坐标是 .
18.在平面直角坐标系中,一次函数和的图象如图所示,则关于的一元一次不等式的解集是 .
三、解答题
19.如图,直线的函数表达式为,且直线与轴交于点.直线与轴交于点,且经过点,直线与交于点.
(1)求点和点的坐标;
(2)求直线的函数表达式;
(3)利用函数图象写出关于,的二元一次方程组的解.
20.已知:如图,在中,点在线段上,,,,求:
(1)直线的解析式;
(2)的面积.
21.已知点、在直线上,和函数的图象交于点,点的横坐标是1.
(1)求直线的表达式;
(2)求关于、的方程组的解及的值.
(3)若点关于轴的对称点为,求的面积.
22.如图,直线与直线相交于点.
(1)求的值;
(2)不解关于、的方程组,请你直接写出它的解;
(3)直线是否也经过点?请说明理由.
23.已知点、在直线上,和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,若点关于轴的对称点为,求的面积.
24.如图,已知直线与轴交于点,且和直线交于点,根据以上信息解答下列问题:
(1)求的值;
(2)不解关于,的方程组,请你直接写出它的解;
(3)判断直线是否也经过点?请说明理由;
(4)若直线,表示的两个一次函数都大于0,此时恰好,求直线的函数解析式.
答案
一、选择题.
1.【分析】几何函数图象,写出直线在直线下方所对应的自变量的范围即可.
【解析】直线和直线的交点坐标为,
当时,.
故选:.
2.【分析】看在轴下方的函数图象所对应的自变量的取值即可.
【解析】由图象可以看出,轴下方的函数图象所对应自变量的取值为,
故不等式的解集是.
故选:.
3.【分析】先根据一次函数的性质画出函数图象,然后结合图象,写出一次函数图象在轴上方所对应的自变量的范围即可.
【解析】如图,当时,,
即当时的取值范围是.
故选:.
4.【分析】根据一次函数的性质即可解决问题;
【解析】观察图象可知直线经过和,
,是方程的解,故正确,
时,,
直线经过点,故正确,
当时,,故正确,
当时,,故错误,
故选:.
5.【分析】先把代入,得出,则两个一次函数的交点的坐标为;那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
【解析】把代入,得出,
函数和的图象交于点,
即,同时满足两个一次函数的解析式.
所以关于,的方程组的解是.
故选:.
6.【分析】根据题意和函数图象中的数据,可以得到方程的解,本题得以解决.
【解析】直线和直线相交于点,
的解是,
即方程的解是,
故选:.
7.【分析】利用函数图象,写出在轴下方且函数的函数值小于函数的函数值对应的自变量的范围即可.
【解析】当时,;当时,,
所以不等式的解集为.
故选:.
8.【分析】仔细观察图象:①根据函数图象直接得到结论;
②的正负看函数从左向右成何趋势,的正负看函数与轴的交点坐标;
③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;
④看两直线都在轴上方的自变量的取值范围.
【解析】由图象可得:对于函数来说,随的增大而减小,故①正确;
由于,,所以函数的图象经过第二,三,四象限,即不经过第一象限,故②正确,
由图象可得当时,一次函数图象在的图象上方,
的解集是,故③正确;
一次函数与的图象的交点的横坐标为3,
,
,故④正确,
故选:.
9.【分析】仔细观察图象:①的正负看函数图象从左向右成何趋势,的正负看函数图象与轴交点即可;②的正负看函数从左向右成何趋势,的正负看函数与轴的交点坐标;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④看两直线都在轴上方的自变量的取值范围.
【解析】由图象可得:,,,,
,故①正确;
函数的图象经过第二,三,四象限,即不经过第一象限,故②正确,
由图象可得当时,一次函数图象在的图象上方,
的解集是,故③正确;
一次函数与的图象的交点的横坐标为3,
,
,故④正确,
故选:.
10.选:.
二、填空题
11.【分析】利用函数图象交点坐标为两函数解析式组成的方程组的解解决问题.
【解析】直线和交于点,
当时,,
即关于的方程的解为.
故答案为.
12.【分析】首先利用待定系数法求出的值,进而得到点坐标,再根据两函数图象的交点就是两函数的解析式组成的二元一次方程组的解可得答案.
【解析】直线经过点,
,
解得,
,
关于,的二元一次方程组的解为,
故答案为.
13.【分析】函数图象交点坐标为两函数解析式组成的方程组的解,据此即可求解.
【解析】二元一次方程组的解为,
函数与的图象的交点坐标为.
故答案为.
14.【分析】根据一次函数与二元一次方程(组的关系即可得结论.
【解析】根据一次函数与二元一次方程(组的关系可知:
直线和直线的交点,即为关于、的方程组的解,
所以关于、的方程组的解为.
故答案为.
15.【分析】首先求出点坐标,再根据两函数图象的交点坐标即为两函数组成的方程组的解.
【解析】直线过点,
,
,
,
方程组的解为:.
故答案为:.
16.【分析】当时,的函数图象在的下方,从而可得到不等式的解集.
【解答】从图象可看出当,直线的图象在直线的上方,不等式.
故答案为:.
17.【分析】根据题意得出方程组,求出方程组的解,再得出答案即可.
【解析】根据题意得:
,
①②,得,
把代入①,得,
解得:,
所以方程组的解为,
两直线交点坐标是,
故答案为:.
18.【分析】写出直线在直线上方所对应的自变量的范围即可.
【解析】由得到:.
根据图象可知:两函数的交点为,
所以关于的一元一次不等式的解集是,即关于的一元一次不等式的解集是,
故答案为:.
三、解答题
19.(1)在中
令,即解得,
,,
点在直线上,
,
,
,;
(2)设直线的函数表达式为,
由题意得:,
解得:,
;
(3)由图可知,二元一次方程组的解为.
20.(1)设直线的解析式为,
把,代入得,
解得,,
直线的解析式为;
(2)把代入得,,
,
,,
.
21.(1)由于点、在直线上,
,
所以直线的表达式为:
(2)由于点在直线上,当时,
所以点的坐标为
因为点是直线与直线的交点,
所以关于、的方程组的解为
把,代入中,
得.
(3)因为点与点关于轴对称,所以点
所以,
所以
.
22.(1)把代入得;
(2)由(1)得,
所以方程组的解为;
(3)直线经过点.理由如下:
因为经过点,
所以,
所以直线也经过点.
23.(1)点、在直线上,
,解得,
所以直线的表达式为:;
(2)由于点在直线上,当时,,
所以点的坐标为,
所以关于、的方程组的解为,
因为点是直线与直线的交点,
把,代入中,求得.
(3)因为点与点关于轴对称,所以点,
所以,,
所以
.
24.(1)在直线上,
当时,;
(2)直线与轴交于点,且和直线交于点,
关于,的方程组的解为;
(3)由(2)知点,
点在直线上,
,
当时,直线,
所以直线也经过点;
(4)直线,表示的两个一次函数都大于0,此时恰好,
直线过点,
又直线过点,
,
解得.
直线的函数解析式为.
一、选择题.
1.在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为
A. B. C. D.无法确定
2.如图,直线交坐标轴于,两点,则不等式的解集为
A. B. C. D.
3.如果直线经过第一、二、四象限,且与轴的交点为,那么当时的取值范围是
A. B. C.x≤6 D.x≥6
4.一次函数的图象如图所示,则下列说法中错误的是
A.,是方程的解 B.直线经过点
C.当时, D.当时,
5.如图,已知函数和图象交于点,点的横坐标为1,则关于,的方程组的解是
A. B. C. D.
6.如图,直线和直线相交于点,根据图象可知,关于的方程的解是
A. B. C.或25 D.
7.如图,已知直线过点,过点的直线交轴于点,则不等式的解集为
A. B. C. D.
8.一次函数与的图象如图所示,下列说法:
①对于函数来说,随的增大而减小
②函数不经过第一象限,
③不等式的解集是,
④,其中正确的个数有
A.4 B.3 C.2 D.1
9.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③不等式的解集是;④.其中正确的个数有
A.4 B.3 C.2 D.1
10.一次函数与的图象如图所示,下列说法:①对于函数来说,随的增大而增大;②函数不经过第二象限;③不等式ax-d≥cx-b的解集是x≥4;④,其中正确的是
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题
11.已知直线和交于点,则关于的方程的解为 .
12.已知直线与相交于点,则关于,的二元一次方程组的解为 .
13.已知二元一次方程组的解为,则在同一平面直角坐标系中,函数与的图象的交点坐标为 .
14.如图,已知直线和直线交于点,则关于、的方程组的解是 .
15.如图,直角坐标系中,直线和直线相交于点,则方程组的解为 .
16.如图,一次函数与正比例函数在同一平面坐标系的图象如图所示,则关于的不等式的解集为 .
17.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)与的交点坐标.据此,则矩阵式所对应两直线交点坐标是 .
18.在平面直角坐标系中,一次函数和的图象如图所示,则关于的一元一次不等式的解集是 .
三、解答题
19.如图,直线的函数表达式为,且直线与轴交于点.直线与轴交于点,且经过点,直线与交于点.
(1)求点和点的坐标;
(2)求直线的函数表达式;
(3)利用函数图象写出关于,的二元一次方程组的解.
20.已知:如图,在中,点在线段上,,,,求:
(1)直线的解析式;
(2)的面积.
21.已知点、在直线上,和函数的图象交于点,点的横坐标是1.
(1)求直线的表达式;
(2)求关于、的方程组的解及的值.
(3)若点关于轴的对称点为,求的面积.
22.如图,直线与直线相交于点.
(1)求的值;
(2)不解关于、的方程组,请你直接写出它的解;
(3)直线是否也经过点?请说明理由.
23.已知点、在直线上,和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,若点关于轴的对称点为,求的面积.
24.如图,已知直线与轴交于点,且和直线交于点,根据以上信息解答下列问题:
(1)求的值;
(2)不解关于,的方程组,请你直接写出它的解;
(3)判断直线是否也经过点?请说明理由;
(4)若直线,表示的两个一次函数都大于0,此时恰好,求直线的函数解析式.
答案
一、选择题.
1.【分析】几何函数图象,写出直线在直线下方所对应的自变量的范围即可.
【解析】直线和直线的交点坐标为,
当时,.
故选:.
2.【分析】看在轴下方的函数图象所对应的自变量的取值即可.
【解析】由图象可以看出,轴下方的函数图象所对应自变量的取值为,
故不等式的解集是.
故选:.
3.【分析】先根据一次函数的性质画出函数图象,然后结合图象,写出一次函数图象在轴上方所对应的自变量的范围即可.
【解析】如图,当时,,
即当时的取值范围是.
故选:.
4.【分析】根据一次函数的性质即可解决问题;
【解析】观察图象可知直线经过和,
,是方程的解,故正确,
时,,
直线经过点,故正确,
当时,,故正确,
当时,,故错误,
故选:.
5.【分析】先把代入,得出,则两个一次函数的交点的坐标为;那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
【解析】把代入,得出,
函数和的图象交于点,
即,同时满足两个一次函数的解析式.
所以关于,的方程组的解是.
故选:.
6.【分析】根据题意和函数图象中的数据,可以得到方程的解,本题得以解决.
【解析】直线和直线相交于点,
的解是,
即方程的解是,
故选:.
7.【分析】利用函数图象,写出在轴下方且函数的函数值小于函数的函数值对应的自变量的范围即可.
【解析】当时,;当时,,
所以不等式的解集为.
故选:.
8.【分析】仔细观察图象:①根据函数图象直接得到结论;
②的正负看函数从左向右成何趋势,的正负看函数与轴的交点坐标;
③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;
④看两直线都在轴上方的自变量的取值范围.
【解析】由图象可得:对于函数来说,随的增大而减小,故①正确;
由于,,所以函数的图象经过第二,三,四象限,即不经过第一象限,故②正确,
由图象可得当时,一次函数图象在的图象上方,
的解集是,故③正确;
一次函数与的图象的交点的横坐标为3,
,
,故④正确,
故选:.
9.【分析】仔细观察图象:①的正负看函数图象从左向右成何趋势,的正负看函数图象与轴交点即可;②的正负看函数从左向右成何趋势,的正负看函数与轴的交点坐标;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④看两直线都在轴上方的自变量的取值范围.
【解析】由图象可得:,,,,
,故①正确;
函数的图象经过第二,三,四象限,即不经过第一象限,故②正确,
由图象可得当时,一次函数图象在的图象上方,
的解集是,故③正确;
一次函数与的图象的交点的横坐标为3,
,
,故④正确,
故选:.
10.选:.
二、填空题
11.【分析】利用函数图象交点坐标为两函数解析式组成的方程组的解解决问题.
【解析】直线和交于点,
当时,,
即关于的方程的解为.
故答案为.
12.【分析】首先利用待定系数法求出的值,进而得到点坐标,再根据两函数图象的交点就是两函数的解析式组成的二元一次方程组的解可得答案.
【解析】直线经过点,
,
解得,
,
关于,的二元一次方程组的解为,
故答案为.
13.【分析】函数图象交点坐标为两函数解析式组成的方程组的解,据此即可求解.
【解析】二元一次方程组的解为,
函数与的图象的交点坐标为.
故答案为.
14.【分析】根据一次函数与二元一次方程(组的关系即可得结论.
【解析】根据一次函数与二元一次方程(组的关系可知:
直线和直线的交点,即为关于、的方程组的解,
所以关于、的方程组的解为.
故答案为.
15.【分析】首先求出点坐标,再根据两函数图象的交点坐标即为两函数组成的方程组的解.
【解析】直线过点,
,
,
,
方程组的解为:.
故答案为:.
16.【分析】当时,的函数图象在的下方,从而可得到不等式的解集.
【解答】从图象可看出当,直线的图象在直线的上方,不等式.
故答案为:.
17.【分析】根据题意得出方程组,求出方程组的解,再得出答案即可.
【解析】根据题意得:
,
①②,得,
把代入①,得,
解得:,
所以方程组的解为,
两直线交点坐标是,
故答案为:.
18.【分析】写出直线在直线上方所对应的自变量的范围即可.
【解析】由得到:.
根据图象可知:两函数的交点为,
所以关于的一元一次不等式的解集是,即关于的一元一次不等式的解集是,
故答案为:.
三、解答题
19.(1)在中
令,即解得,
,,
点在直线上,
,
,
,;
(2)设直线的函数表达式为,
由题意得:,
解得:,
;
(3)由图可知,二元一次方程组的解为.
20.(1)设直线的解析式为,
把,代入得,
解得,,
直线的解析式为;
(2)把代入得,,
,
,,
.
21.(1)由于点、在直线上,
,
所以直线的表达式为:
(2)由于点在直线上,当时,
所以点的坐标为
因为点是直线与直线的交点,
所以关于、的方程组的解为
把,代入中,
得.
(3)因为点与点关于轴对称,所以点
所以,
所以
.
22.(1)把代入得;
(2)由(1)得,
所以方程组的解为;
(3)直线经过点.理由如下:
因为经过点,
所以,
所以直线也经过点.
23.(1)点、在直线上,
,解得,
所以直线的表达式为:;
(2)由于点在直线上,当时,,
所以点的坐标为,
所以关于、的方程组的解为,
因为点是直线与直线的交点,
把,代入中,求得.
(3)因为点与点关于轴对称,所以点,
所以,,
所以
.
24.(1)在直线上,
当时,;
(2)直线与轴交于点,且和直线交于点,
关于,的方程组的解为;
(3)由(2)知点,
点在直线上,
,
当时,直线,
所以直线也经过点;
(4)直线,表示的两个一次函数都大于0,此时恰好,
直线过点,
又直线过点,
,
解得.
直线的函数解析式为.
