八年级数学下册试题 四边形(基础练习)-沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 四边形(基础练习)-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 21:18:13 | ||
图片预览



文档简介
四边形(基础练习)
一、单选题
1.如图,小陈在木门板上钉了一个加固板,从数学的角度看,这样做的道理是( )
A.利用四边形的不稳定性
B.利用三角形的稳定性
C.三角形两边之和大于第三边
D.四边形的外角和等于360°
2.以上四个条件中可以判定四边形是平行四边形的有( )
①两组对边分别平行;
②两组对边分别相等;
③有一组对边平行且相等;
④对角线相等.
A.1个 B.2个 C.3个 D.4个
3.如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )
A.1个 B.2个 C.3个 D.4个
4.若是非零向量,则下列等式正确的是( )
A.||=|| B.||+||=0 C.+=0 D.=
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
6.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90° C.AC⊥BD D.∠1=∠2
二、填空题
7.若一个多边形的每个外角都为36°,则这个多边形的内角和是 °.
8.一个多边形的内角和是外角和的4倍,则此多边形的边数是 .
9.在 ABCD中,AB=3,BC=4,则 ABCD的周长等于 .
10.如图,在 ABCD中,对角线AC,BD相交于点O,添加一个条件判定 ABCD是菱形,所添条件为 (写出一个即可)
11.如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件: ,使得加上这个条件后能够推出AD∥BC且AB=CD.
12.如果向量与单位向量方向相反,且长度为2,那么用向量表示= ﹣
13.化简:= .
14.如图,在矩形ABCD中,已知AB=3,BC=4,则BD= .
15.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .
16.正方形ABCD中,AC=4,则正方形ABCD面积为 .
17.如图,在 ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF= .
18.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
三、解答题
19.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
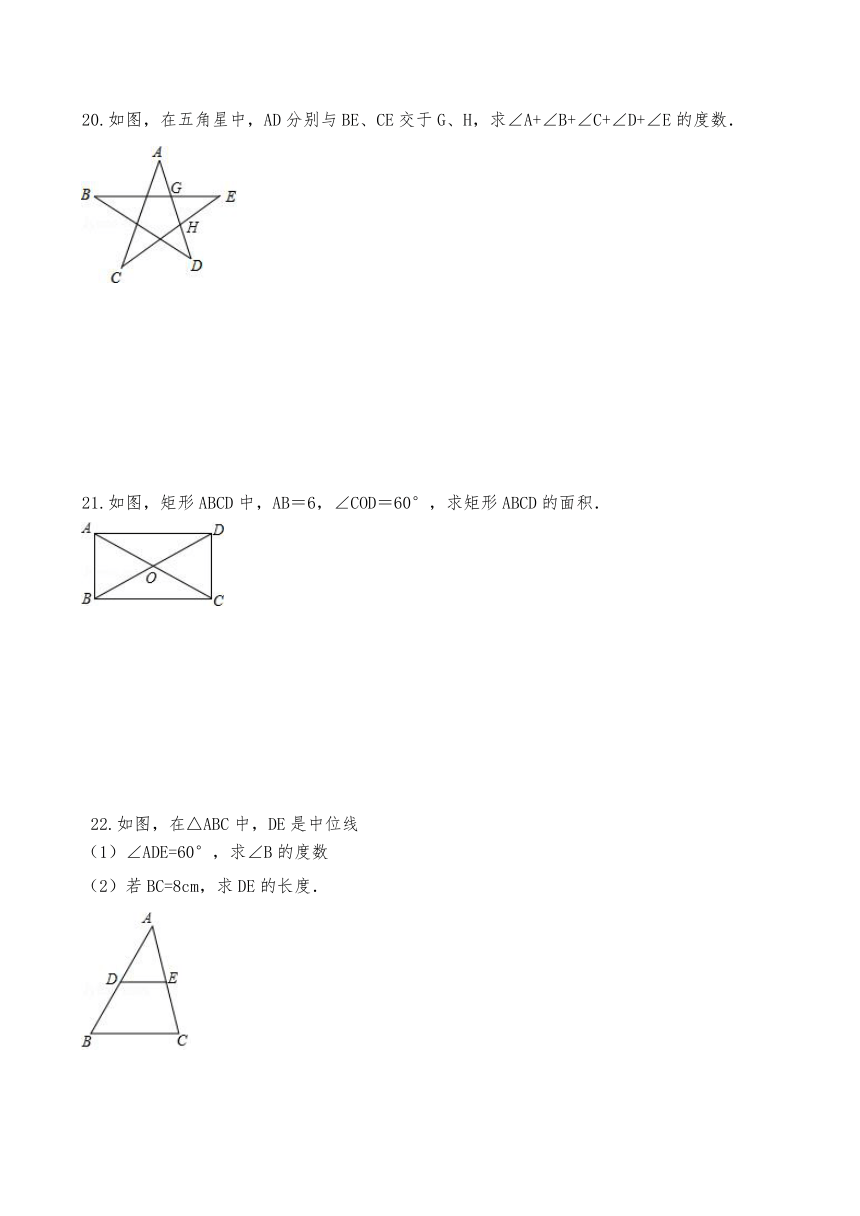
20.如图,在五角星中,AD分别与BE、CE交于G、H,求∠A+∠B+∠C+∠D+∠E的度数.
21.如图,矩形ABCD中,AB=6,∠COD=60°,求矩形ABCD的面积.
22.如图,在△ABC中,DE是中位线
(1)∠ADE=60°,求∠B的度数
(2)若BC=8cm,求DE的长度.
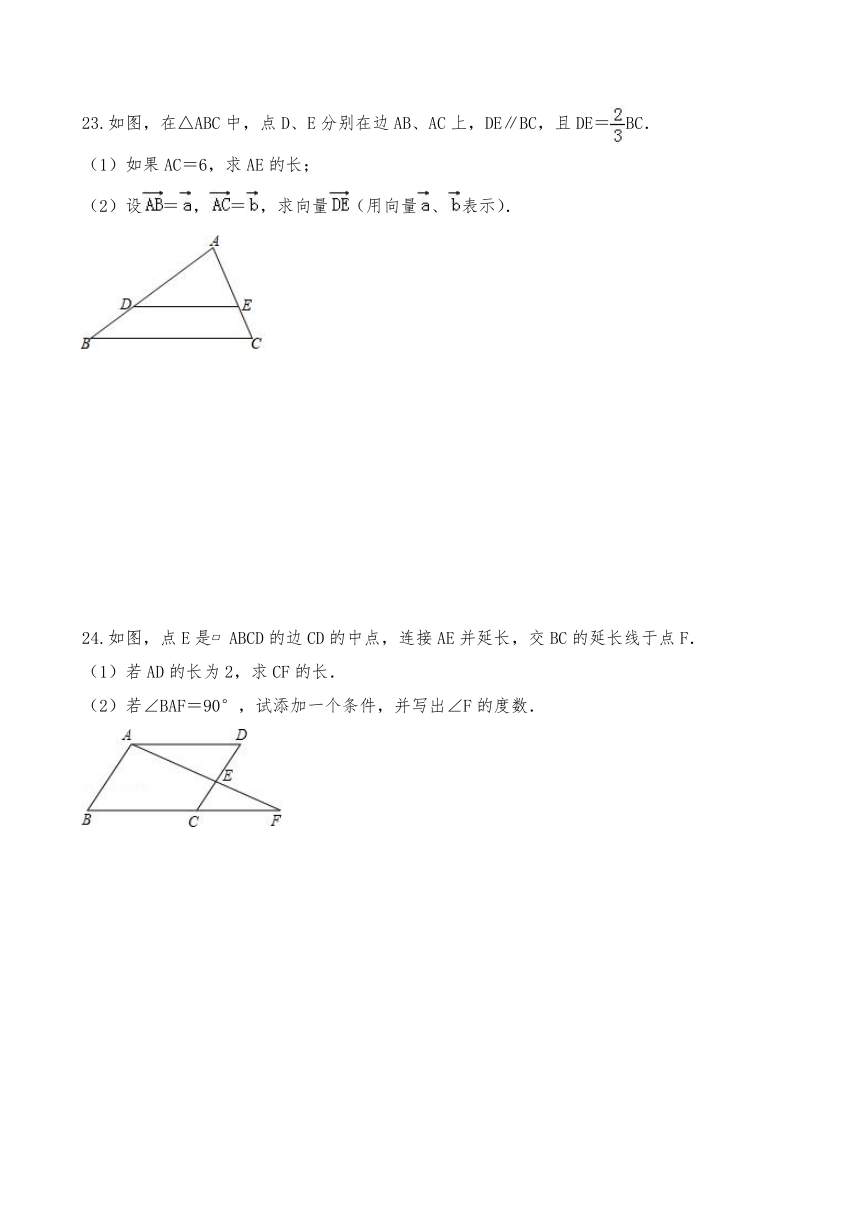
23.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE=BC.
(1)如果AC=6,求AE的长;
(2)设=,=,求向量(用向量、表示).
24.如图,点E是 ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)若AD的长为2,求CF的长.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
答案
一、单选题
1.B
【分析】此题根据题目的意思,钉了一个加固板,即分割成了三角形,故利用了三角形的稳定性.
【解答】解:这样做的原因是:利用三角形的稳定性使门板不变形.
故选:B.
2.C
【分析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.按照平行四边形的判定方法进行判断即可.
【解答】解:①两组对边分别平行,符合平行四边形的定义,故①正确;
②两组对边分别相等,符合平行四边形的判定条件,故②正确;
③由一组对边平行且相等,符合平行四边形的判定条件,故③正确;
④对角线互相平分的四边形是平行四边形,故④错误;
所以正确的结论有三个:①②③,
故选:C.
3.C
【分析】根据三角形的中位线定理得出EF∥AB,DF∥BC,DE∥AC,根据有两组对边分别平行的四边形是平行四边形推出即可.
【解答】解:有3个平行四边形,有平行四边形ADEF,平行四边形CFDE,平行四边形BEFD,
理由是:∵D、E、F分别是△ABC的边AB、BC、CA的中点,
∴EF∥AB,DF∥BC,
∴四边形BEFD是平行四边形,
同理四边形ADEF是平行四边形,四边形CFDE是平行四边形,
∴图中平行四边形一共有3个,
故选:C.
4.A
【分析】长度不为0的向量叫做非零向量,本题根据向量的长度及方向易得结果.
【解答】解:∵是非零向量,
∴||=||.
+=
故选:A.
5.C
【分析】由矩形的性质得∠A=∠ABC=90°,由折叠的性质得∠BA'E=∠A=90°,∠A'BE=∠ABE=(90°﹣∠DBC)=33°,即可得出答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°;
故选:C.
6.B
【分析】根据一个角是90°的平行四边形是矩形进行选择即可.
【解答】解:A、AB=BC,邻边相等,可判定平行四边形ABCD是菱形,不符合题意;
B、一内角等于90°,可判断平行四边形ABCD成为矩形,符合题意;
C、对角线互相垂直,可判定平行四边形ABCD是菱形,不符合题意;
D、对角线平分对角,可判断平行四边形ABCD成为菱形,不符合题意;
故选:B.
二、填空题
7.1440
【分析】本题首先根据多边形外角和定理,即任意多边形外角和为360°,可求出此正多边形的边数为10.然后再根据三角形的内角和定理求出它的内角和.
【解答】解:∵此正多边形每一个外角都为36°,
360°÷36°=10,
∴此正多边形的边数为10.
则这个多边形的内角和为(10﹣2)×180°=1440°.
故答案为:1440.
8.10
【分析】任何多边形的外角和是360度,内角和是外角和的4倍,则内角和是4×360度.n边形的内角和是(n﹣2) 180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.
【解答】解:设边数为n,则
(n﹣2) 180°=4×360°,
解得:n=10.
则多边形的边数是10.
9.14
【分析】根据平行四边形的对边相等,可得AB=CD,AD=BC,所以可求得 ABCD的周长为14.
【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=4,
∴ ABCD的周长为14.
故答案为14.
10.AB=AD
【分析】根据一组邻边相等的平行四边形是菱形,对角线互相垂直的平行四边形是菱形可得解.
【解答】解:根据一组邻边相等的平行四边形是菱形,则可添加条件为:AB=AD(AD=CD,BC=CD,AB=BC)
也可添加∠1=∠2,根据平行四边形的性质,可求AD=CD.
根据对角线互相垂直的平行四边形是菱形,则可添加条件为:AC⊥BD.
故答案为:AB=AD(答案不唯一)
11.∠DAC=∠ADB或∠BAD=∠CDA或∠DBC=∠ACB或∠ABC=∠DCB或OB=OC或OA=OD
【分析】先证四边形AECO是梯形,再说明是等腰梯形.由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA,同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
【解答】解:由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,
则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA
∴△BAD≌△CDA
∴BD=AC,AB=DC,
∵∠DAC=∠ADB,
∴OA=OD,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠AOD=∠BOC,
∴∠DAC=∠ACB=∠ADB=∠DBC,
∴AD∥BC
同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
本题答案不唯一,如∠DAC=∠ADB,∠BAD=∠CDA,∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD.(任选其一)
12.【分析】根据向量的表示方法可直接进行解答.
【解答】解:∵的长度为2,向量是单位向量,
∴a=2e,
∵与单位向量的方向相反,
∴=﹣2.
故答案为:﹣2.
13.【分析】平面向量的加减计算法则与实数的加减计算法则相同.
【解答】解:原式=﹣+=+.
故答案是:+.
14.5
【分析】根据勾股定理可直接算出BD的长度
【解答】解:由勾股定理可知,
故答案为5.
15.24
【分析】因为菱形的面积为两条对角线积的一半,所以这个菱形的面积为24.
【解答】解:∵菱形的两条对角线长分别是6和8,
∴这个菱形的面积为6×8÷2=24
故答案为24
16.8
【分析】正方形是特殊的菱形,故根据菱形的面积计算公式即可求正方形ABCD的面积,即可解题.
【解答】解:∵AC的长为4,
∴正方形ABCD的面积为×42=8,
故答案为:8.
17.3
【分析】由四边形ABCD是平行四边形,根据平行四边形的对边相等,可得BC=AD=8,又由点E、F分别是BD、CD的中点,利用三角形中位线的性质,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵点E、F分别是BD、CD的中点,
∴EF=BC=×6=3.
故答案为:3.
18.120
【分析】根据平行四边形的对边平行,对角相等,可得AD∥BC,∠B=∠D,∠A=∠C,易得∠C=2∠D,∠C+∠D=180°,解方程组即可求得.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
三、解答题
19.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
20.解:由三角形的外角性质得,∠GHE=∠A+∠C,∠HGE=∠B+∠D,
∵∠GHE+∠HGE+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:∵四边形ABCD是矩形
∴AO=BO=CO=DO,∠DCB=90°,AB=CD=6
∵∠COD=60°,CO=DO
∴△COD是等边三角形
∴CO=DO=CD=6
∴BD=12
∴BC==6
∴S矩形ABCD=6×6=36
22.解:(1)∵DE是中位线,
∴DE∥BC,
∴∠B=∠ADE=60°;
(2)∵DE是中位线,
∴DE=AB=4cm.
23.解:(1)如图,∵DE∥BC,且DE=BC,
∴==.
又AC=6,
∴AE=4.
(2)∵=,=,
∴=﹣=﹣.
又DE∥BC,DE=BC,
∴==(﹣).
24.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,,
∴△ADE≌△FCE(AAS),
∴CF=AD=2;
(2)∵∠BAF=90°,
添加一个条件:当∠B=60°时,∠F=90°﹣60°=30°(答案不唯一).
25.解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=∠ABC=30°,
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,
∴OB==,
∴AC=2OA=2cm,BD=2OB=2cm;
(2)S菱形ABCD=AC BD=×2×2=2(cm2).
一、单选题
1.如图,小陈在木门板上钉了一个加固板,从数学的角度看,这样做的道理是( )
A.利用四边形的不稳定性
B.利用三角形的稳定性
C.三角形两边之和大于第三边
D.四边形的外角和等于360°
2.以上四个条件中可以判定四边形是平行四边形的有( )
①两组对边分别平行;
②两组对边分别相等;
③有一组对边平行且相等;
④对角线相等.
A.1个 B.2个 C.3个 D.4个
3.如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )
A.1个 B.2个 C.3个 D.4个
4.若是非零向量,则下列等式正确的是( )
A.||=|| B.||+||=0 C.+=0 D.=
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
6.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90° C.AC⊥BD D.∠1=∠2
二、填空题
7.若一个多边形的每个外角都为36°,则这个多边形的内角和是 °.
8.一个多边形的内角和是外角和的4倍,则此多边形的边数是 .
9.在 ABCD中,AB=3,BC=4,则 ABCD的周长等于 .
10.如图,在 ABCD中,对角线AC,BD相交于点O,添加一个条件判定 ABCD是菱形,所添条件为 (写出一个即可)
11.如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件: ,使得加上这个条件后能够推出AD∥BC且AB=CD.
12.如果向量与单位向量方向相反,且长度为2,那么用向量表示= ﹣
13.化简:= .
14.如图,在矩形ABCD中,已知AB=3,BC=4,则BD= .
15.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .
16.正方形ABCD中,AC=4,则正方形ABCD面积为 .
17.如图,在 ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF= .
18.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
三、解答题
19.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
20.如图,在五角星中,AD分别与BE、CE交于G、H,求∠A+∠B+∠C+∠D+∠E的度数.
21.如图,矩形ABCD中,AB=6,∠COD=60°,求矩形ABCD的面积.
22.如图,在△ABC中,DE是中位线
(1)∠ADE=60°,求∠B的度数
(2)若BC=8cm,求DE的长度.
23.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE=BC.
(1)如果AC=6,求AE的长;
(2)设=,=,求向量(用向量、表示).
24.如图,点E是 ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)若AD的长为2,求CF的长.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
答案
一、单选题
1.B
【分析】此题根据题目的意思,钉了一个加固板,即分割成了三角形,故利用了三角形的稳定性.
【解答】解:这样做的原因是:利用三角形的稳定性使门板不变形.
故选:B.
2.C
【分析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.按照平行四边形的判定方法进行判断即可.
【解答】解:①两组对边分别平行,符合平行四边形的定义,故①正确;
②两组对边分别相等,符合平行四边形的判定条件,故②正确;
③由一组对边平行且相等,符合平行四边形的判定条件,故③正确;
④对角线互相平分的四边形是平行四边形,故④错误;
所以正确的结论有三个:①②③,
故选:C.
3.C
【分析】根据三角形的中位线定理得出EF∥AB,DF∥BC,DE∥AC,根据有两组对边分别平行的四边形是平行四边形推出即可.
【解答】解:有3个平行四边形,有平行四边形ADEF,平行四边形CFDE,平行四边形BEFD,
理由是:∵D、E、F分别是△ABC的边AB、BC、CA的中点,
∴EF∥AB,DF∥BC,
∴四边形BEFD是平行四边形,
同理四边形ADEF是平行四边形,四边形CFDE是平行四边形,
∴图中平行四边形一共有3个,
故选:C.
4.A
【分析】长度不为0的向量叫做非零向量,本题根据向量的长度及方向易得结果.
【解答】解:∵是非零向量,
∴||=||.
+=
故选:A.
5.C
【分析】由矩形的性质得∠A=∠ABC=90°,由折叠的性质得∠BA'E=∠A=90°,∠A'BE=∠ABE=(90°﹣∠DBC)=33°,即可得出答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°;
故选:C.
6.B
【分析】根据一个角是90°的平行四边形是矩形进行选择即可.
【解答】解:A、AB=BC,邻边相等,可判定平行四边形ABCD是菱形,不符合题意;
B、一内角等于90°,可判断平行四边形ABCD成为矩形,符合题意;
C、对角线互相垂直,可判定平行四边形ABCD是菱形,不符合题意;
D、对角线平分对角,可判断平行四边形ABCD成为菱形,不符合题意;
故选:B.
二、填空题
7.1440
【分析】本题首先根据多边形外角和定理,即任意多边形外角和为360°,可求出此正多边形的边数为10.然后再根据三角形的内角和定理求出它的内角和.
【解答】解:∵此正多边形每一个外角都为36°,
360°÷36°=10,
∴此正多边形的边数为10.
则这个多边形的内角和为(10﹣2)×180°=1440°.
故答案为:1440.
8.10
【分析】任何多边形的外角和是360度,内角和是外角和的4倍,则内角和是4×360度.n边形的内角和是(n﹣2) 180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.
【解答】解:设边数为n,则
(n﹣2) 180°=4×360°,
解得:n=10.
则多边形的边数是10.
9.14
【分析】根据平行四边形的对边相等,可得AB=CD,AD=BC,所以可求得 ABCD的周长为14.
【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=4,
∴ ABCD的周长为14.
故答案为14.
10.AB=AD
【分析】根据一组邻边相等的平行四边形是菱形,对角线互相垂直的平行四边形是菱形可得解.
【解答】解:根据一组邻边相等的平行四边形是菱形,则可添加条件为:AB=AD(AD=CD,BC=CD,AB=BC)
也可添加∠1=∠2,根据平行四边形的性质,可求AD=CD.
根据对角线互相垂直的平行四边形是菱形,则可添加条件为:AC⊥BD.
故答案为:AB=AD(答案不唯一)
11.∠DAC=∠ADB或∠BAD=∠CDA或∠DBC=∠ACB或∠ABC=∠DCB或OB=OC或OA=OD
【分析】先证四边形AECO是梯形,再说明是等腰梯形.由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA,同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
【解答】解:由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,
则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA
∴△BAD≌△CDA
∴BD=AC,AB=DC,
∵∠DAC=∠ADB,
∴OA=OD,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠AOD=∠BOC,
∴∠DAC=∠ACB=∠ADB=∠DBC,
∴AD∥BC
同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=CD.
本题答案不唯一,如∠DAC=∠ADB,∠BAD=∠CDA,∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD.(任选其一)
12.【分析】根据向量的表示方法可直接进行解答.
【解答】解:∵的长度为2,向量是单位向量,
∴a=2e,
∵与单位向量的方向相反,
∴=﹣2.
故答案为:﹣2.
13.【分析】平面向量的加减计算法则与实数的加减计算法则相同.
【解答】解:原式=﹣+=+.
故答案是:+.
14.5
【分析】根据勾股定理可直接算出BD的长度
【解答】解:由勾股定理可知,
故答案为5.
15.24
【分析】因为菱形的面积为两条对角线积的一半,所以这个菱形的面积为24.
【解答】解:∵菱形的两条对角线长分别是6和8,
∴这个菱形的面积为6×8÷2=24
故答案为24
16.8
【分析】正方形是特殊的菱形,故根据菱形的面积计算公式即可求正方形ABCD的面积,即可解题.
【解答】解:∵AC的长为4,
∴正方形ABCD的面积为×42=8,
故答案为:8.
17.3
【分析】由四边形ABCD是平行四边形,根据平行四边形的对边相等,可得BC=AD=8,又由点E、F分别是BD、CD的中点,利用三角形中位线的性质,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵点E、F分别是BD、CD的中点,
∴EF=BC=×6=3.
故答案为:3.
18.120
【分析】根据平行四边形的对边平行,对角相等,可得AD∥BC,∠B=∠D,∠A=∠C,易得∠C=2∠D,∠C+∠D=180°,解方程组即可求得.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
三、解答题
19.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
20.解:由三角形的外角性质得,∠GHE=∠A+∠C,∠HGE=∠B+∠D,
∵∠GHE+∠HGE+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:∵四边形ABCD是矩形
∴AO=BO=CO=DO,∠DCB=90°,AB=CD=6
∵∠COD=60°,CO=DO
∴△COD是等边三角形
∴CO=DO=CD=6
∴BD=12
∴BC==6
∴S矩形ABCD=6×6=36
22.解:(1)∵DE是中位线,
∴DE∥BC,
∴∠B=∠ADE=60°;
(2)∵DE是中位线,
∴DE=AB=4cm.
23.解:(1)如图,∵DE∥BC,且DE=BC,
∴==.
又AC=6,
∴AE=4.
(2)∵=,=,
∴=﹣=﹣.
又DE∥BC,DE=BC,
∴==(﹣).
24.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,,
∴△ADE≌△FCE(AAS),
∴CF=AD=2;
(2)∵∠BAF=90°,
添加一个条件:当∠B=60°时,∠F=90°﹣60°=30°(答案不唯一).
25.解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=∠ABC=30°,
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,
∴OB==,
∴AC=2OA=2cm,BD=2OB=2cm;
(2)S菱形ABCD=AC BD=×2×2=2(cm2).
