二次函数27.3测试卷(二)(浙江省绍兴市诸暨市)
文档属性
| 名称 | 二次函数27.3测试卷(二)(浙江省绍兴市诸暨市) |  | |
| 格式 | rar | ||
| 文件大小 | 230.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-13 14:32:00 | ||
图片预览


文档简介
二次函数 单元测试卷(二)
(测试内容: 27.3)
(测试时间:100分钟 满分:100分)
一、选一选(每空3分,共30分)
1. 关于二次函数y=(x+2)2-3的最大(小)值,叙述正确的是( )
(A)当x=2时,有最大值-3 (B)当x=-2时,有最大值-3
(C)当x=2时,有最小值-3 (D)当x=-2时,有最小值-3
2. 抛物线y=(x-12)2+6的顶点坐标是( )
A、(-12,6) B、(12,-6) C、(12,6) D、(-12,-6)
3. 将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线,其解析式是( )
(A)y=2(x+1)2+3 (B) y=2(x-1)2-3 (C) y=2(x+1)2-3 (D) y=2(x-1)2+3
4. 已知如图,直线y=x与二次函数y=ax2-2x-1的图像的一个交点M的横坐标为1,则a的值为( )
A.2 B.1 C.3 D.4
5. 对于二次函数,我们把使函数值等于的实数叫做这个函数的零点,则二次函数(为实数)的零点的个数是( )
A.1 B.2 C.0 D.不能确定
6. 把一个小球以20 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:h=20t-5t2.当h=20时,小球的运动时间为( )
A.20 s B.2 s C.(2+2) s D.(2-2) s
7. 在某次实验中,测得两个变量和之间的4组对应数据如下表:
1 2 3 4
0.01 2.9 8.03 15.1
则与之间的关系最接近于下列各关系式中的( )
A. B. C. D.
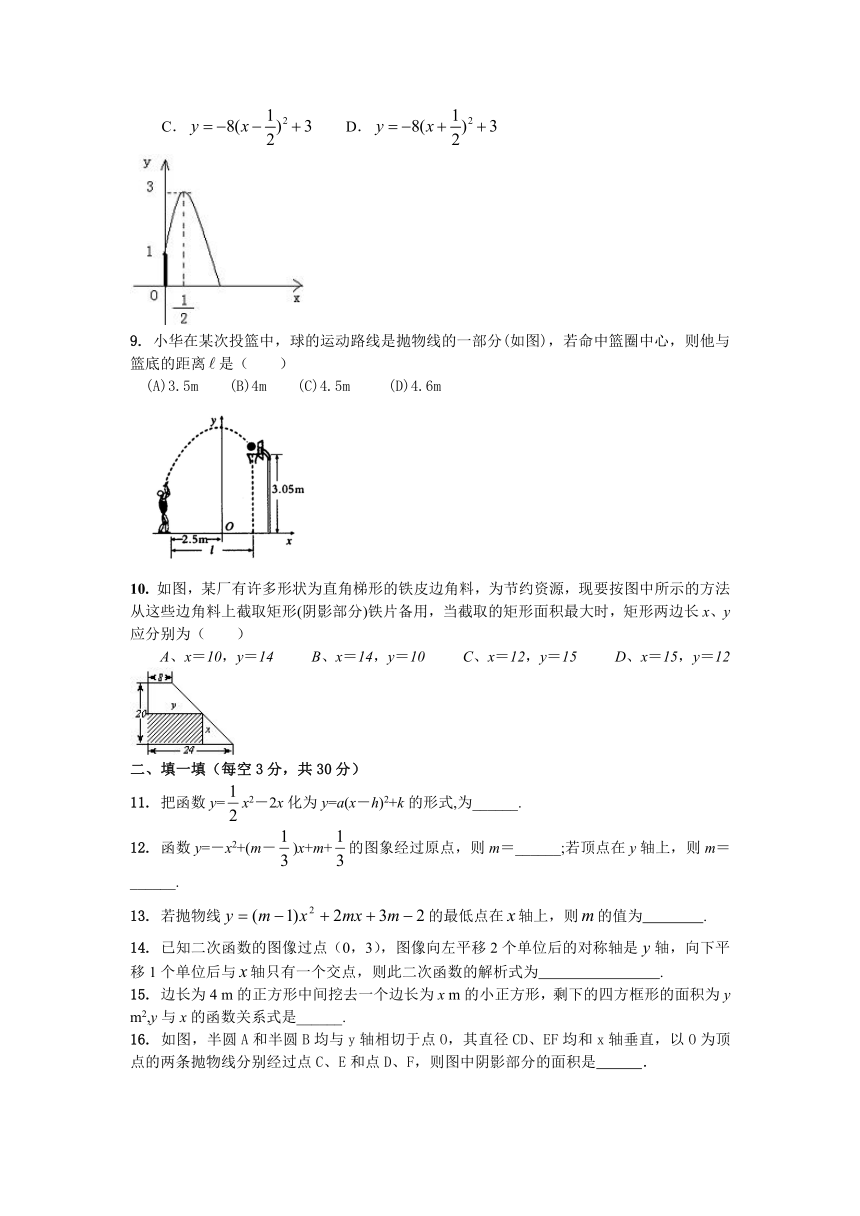
8. 巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高为1米的喷水管喷水最大高度为3米,此时喷水水平距离为 米,在如图4所示的坐标系中,这支喷泉满足的函数关系式是( )
A. B.
C. D.
9. 小华在某次投篮中,球的运动路线是抛物线的一部分(如图),若命中篮圈中心,则他与篮底的距离是( )
(A)3.5m (B)4m (C)4.5m (D)4.6m
10. 如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为( )
A、x=10,y=14 B、x=14,y=10 C、x=12,y=15 D、x=15,y=12
二、填一填(每空3分,共30分)
11. 把函数y=x2-2x化为y=a(x-h)2+k的形式,为______.
12. 函数y=-x2+(m-)x+m+的图象经过原点,则m=______;若顶点在y轴上,则m=______.
13. 若抛物线的最低点在轴上,则的值为 .
14. 已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是轴,向下平移1个单位后与轴只有一个交点,则此二次函数的解析式为 .
15. 边长为4 m的正方形中间挖去一个边长为x m的小正方形,剩下的四方框形的面积为y m2,y与x的函数关系式是______.
16. 如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是 .
17. 已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=2,且当x1=,x2=π,x3=0时,二次函数y的对应值分别为y1,y2,y3,那么y1,y2,y3的大小顺序是_________.
18. 某商场销售一批名牌西裤,平均每天可售出20条,每条赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取降价措施,经调查发现,如果每条西裤每降价1元,那么商场每天可多售出2条.设每条西裤降价x元,商场每天赢利y元,则y与x的函数关系是 ,y是x的 函数.
19. 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离是 米(精确到1米).
20. 某产品每件成本10元,试销阶段每件产品的日销售价(元)与产品的日销售量(件)之间的关系如下表:
(元) 15 20 25 30 …
(件) 25 20 15 10 …
要使每日的销售利润最大,每件产品的销售价应定为 元,此时每日销售利润是 元.
三、解答题(本大题共6小题,共40分)
21.(本题6分)已知函数的图像过点(-1,15),设其图像与轴交于点A、B,点C在图像上,且,求点C的坐标.
22.(本题6分)丁丁推铅球的出手高度为,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
23.(本题6分)某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
24.(本题6分)善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间(单位:分钟)与学习收益量的关系如图1所示,用于回顾反思的时间(单位:分钟)与学习收益的关系如图2所示(其中是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量与用于解题的时间之间的函数关系式;
(2)求小迪回顾反思的学习收益量与用于回顾反思的时间的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
25.(本题8分)用长为l2 m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.问当x取什么值时,S最大 并求出S的最大值.
26.(本题8分)已知,在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2.若以O为坐标原点,OA所在直线为轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线(≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
参考答案
1. D 2. C 3. A 4. D 5. B 6. B 7. B 8. C 9. B 10. D
11. y=0.5(x-2)2-2 12. - 13. 2 14.
15. y=16-x2 16. 17. a小于0时,y118. y=-2x2+60x+800,二次 19. 18 20. 25 225
21.C(,1)或(,1)、(3,-1)
22. 由题意知,点在抛物线上,
所以.解这个方程,得或(舍去).
所以,该抛物线的解析式为.
当时,有,解得,(舍去).
所以,铅球的落点与丁丁的距离为.
23.⑴ y=(x-50) w=(x-50) (-2x+240)=-2x2+340x-12000,
∴y与x的关系式为:y=-2x2+340x-12000.
⑵ y=-2x2+340x-12000=-2 (x-85) 2+2450,
∴当x=85时,y的值最大.
⑶ 当y=2250时,可得方程 -2 (x-85 )2 +2450=2250.解这个方程,得 x1=75,x2=95.根据题意,x2=95不合题意应舍去.
∴当销售单价为75元时,可获得销售利润2250元.
24.(1)由图1,设.当时,,
解得,.
(2)由图2,当时,设.
当时,,..
,即.
当时,.因此
(3)设小迪用于回顾反思的时间为分钟,
学习收益总量为,则她用于解题的时间为分钟.
当时,.
当时,.当时,.
随的增大而减小,因此当时,.
综上,当时,,此时.
答:小迪用于回顾反思的时间为3分钟,用于解题的时间为17分钟时,学习收益总量最大.
25.连结EC,作DF⊥EC,垂足为F
∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°,∵DE=CD .∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,∴四边形EABC为矩形, ∴DE=x m,
∴AE=6-x,DF=x,EC=.s= (0当x=4m时,S最大=12 m2.
26.(1)过点C作CH⊥轴,垂足为H.C点坐标为(,3).
(2)抛物线(≠0)经过C(,3)、A(,0)两点.此抛物线的解析式为:.
(3)存在.因为的顶点坐标为(,3)即为点C.
MP⊥轴,设垂足为N,PN=,因为∠BOA=300,所以ON=.
∴P(,).
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E.把代入得:.∴ M(,),E(,).
同理:Q(,),D(,1).
要使四边形CDPM为等腰梯形,只需CE=QD.
即,解得:,(舍).∴ P点坐标为(,).
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(,).
O
y
x
1.6m
(测试内容: 27.3)
(测试时间:100分钟 满分:100分)
一、选一选(每空3分,共30分)
1. 关于二次函数y=(x+2)2-3的最大(小)值,叙述正确的是( )
(A)当x=2时,有最大值-3 (B)当x=-2时,有最大值-3
(C)当x=2时,有最小值-3 (D)当x=-2时,有最小值-3
2. 抛物线y=(x-12)2+6的顶点坐标是( )
A、(-12,6) B、(12,-6) C、(12,6) D、(-12,-6)
3. 将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线,其解析式是( )
(A)y=2(x+1)2+3 (B) y=2(x-1)2-3 (C) y=2(x+1)2-3 (D) y=2(x-1)2+3
4. 已知如图,直线y=x与二次函数y=ax2-2x-1的图像的一个交点M的横坐标为1,则a的值为( )
A.2 B.1 C.3 D.4
5. 对于二次函数,我们把使函数值等于的实数叫做这个函数的零点,则二次函数(为实数)的零点的个数是( )
A.1 B.2 C.0 D.不能确定
6. 把一个小球以20 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:h=20t-5t2.当h=20时,小球的运动时间为( )
A.20 s B.2 s C.(2+2) s D.(2-2) s
7. 在某次实验中,测得两个变量和之间的4组对应数据如下表:
1 2 3 4
0.01 2.9 8.03 15.1
则与之间的关系最接近于下列各关系式中的( )
A. B. C. D.
8. 巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高为1米的喷水管喷水最大高度为3米,此时喷水水平距离为 米,在如图4所示的坐标系中,这支喷泉满足的函数关系式是( )
A. B.
C. D.
9. 小华在某次投篮中,球的运动路线是抛物线的一部分(如图),若命中篮圈中心,则他与篮底的距离是( )
(A)3.5m (B)4m (C)4.5m (D)4.6m
10. 如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为( )
A、x=10,y=14 B、x=14,y=10 C、x=12,y=15 D、x=15,y=12
二、填一填(每空3分,共30分)
11. 把函数y=x2-2x化为y=a(x-h)2+k的形式,为______.
12. 函数y=-x2+(m-)x+m+的图象经过原点,则m=______;若顶点在y轴上,则m=______.
13. 若抛物线的最低点在轴上,则的值为 .
14. 已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是轴,向下平移1个单位后与轴只有一个交点,则此二次函数的解析式为 .
15. 边长为4 m的正方形中间挖去一个边长为x m的小正方形,剩下的四方框形的面积为y m2,y与x的函数关系式是______.
16. 如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是 .
17. 已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=2,且当x1=,x2=π,x3=0时,二次函数y的对应值分别为y1,y2,y3,那么y1,y2,y3的大小顺序是_________.
18. 某商场销售一批名牌西裤,平均每天可售出20条,每条赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取降价措施,经调查发现,如果每条西裤每降价1元,那么商场每天可多售出2条.设每条西裤降价x元,商场每天赢利y元,则y与x的函数关系是 ,y是x的 函数.
19. 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离是 米(精确到1米).
20. 某产品每件成本10元,试销阶段每件产品的日销售价(元)与产品的日销售量(件)之间的关系如下表:
(元) 15 20 25 30 …
(件) 25 20 15 10 …
要使每日的销售利润最大,每件产品的销售价应定为 元,此时每日销售利润是 元.
三、解答题(本大题共6小题,共40分)
21.(本题6分)已知函数的图像过点(-1,15),设其图像与轴交于点A、B,点C在图像上,且,求点C的坐标.
22.(本题6分)丁丁推铅球的出手高度为,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
23.(本题6分)某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
24.(本题6分)善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间(单位:分钟)与学习收益量的关系如图1所示,用于回顾反思的时间(单位:分钟)与学习收益的关系如图2所示(其中是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量与用于解题的时间之间的函数关系式;
(2)求小迪回顾反思的学习收益量与用于回顾反思的时间的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
25.(本题8分)用长为l2 m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.问当x取什么值时,S最大 并求出S的最大值.
26.(本题8分)已知,在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2.若以O为坐标原点,OA所在直线为轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线(≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
参考答案
1. D 2. C 3. A 4. D 5. B 6. B 7. B 8. C 9. B 10. D
11. y=0.5(x-2)2-2 12. - 13. 2 14.
15. y=16-x2 16. 17. a小于0时,y1
21.C(,1)或(,1)、(3,-1)
22. 由题意知,点在抛物线上,
所以.解这个方程,得或(舍去).
所以,该抛物线的解析式为.
当时,有,解得,(舍去).
所以,铅球的落点与丁丁的距离为.
23.⑴ y=(x-50) w=(x-50) (-2x+240)=-2x2+340x-12000,
∴y与x的关系式为:y=-2x2+340x-12000.
⑵ y=-2x2+340x-12000=-2 (x-85) 2+2450,
∴当x=85时,y的值最大.
⑶ 当y=2250时,可得方程 -2 (x-85 )2 +2450=2250.解这个方程,得 x1=75,x2=95.根据题意,x2=95不合题意应舍去.
∴当销售单价为75元时,可获得销售利润2250元.
24.(1)由图1,设.当时,,
解得,.
(2)由图2,当时,设.
当时,,..
,即.
当时,.因此
(3)设小迪用于回顾反思的时间为分钟,
学习收益总量为,则她用于解题的时间为分钟.
当时,.
当时,.当时,.
随的增大而减小,因此当时,.
综上,当时,,此时.
答:小迪用于回顾反思的时间为3分钟,用于解题的时间为17分钟时,学习收益总量最大.
25.连结EC,作DF⊥EC,垂足为F
∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°,∵DE=CD .∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,∴四边形EABC为矩形, ∴DE=x m,
∴AE=6-x,DF=x,EC=.s= (0
26.(1)过点C作CH⊥轴,垂足为H.C点坐标为(,3).
(2)抛物线(≠0)经过C(,3)、A(,0)两点.此抛物线的解析式为:.
(3)存在.因为的顶点坐标为(,3)即为点C.
MP⊥轴,设垂足为N,PN=,因为∠BOA=300,所以ON=.
∴P(,).
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E.把代入得:.∴ M(,),E(,).
同理:Q(,),D(,1).
要使四边形CDPM为等腰梯形,只需CE=QD.
即,解得:,(舍).∴ P点坐标为(,).
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(,).
O
y
x
1.6m
