列联表独立性分析案例(福建省福州市鼓楼区)
文档属性
| 名称 | 列联表独立性分析案例(福建省福州市鼓楼区) |

|
|
| 格式 | rar | ||
| 文件大小 | 63.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-13 00:00:00 | ||
图片预览






文档简介
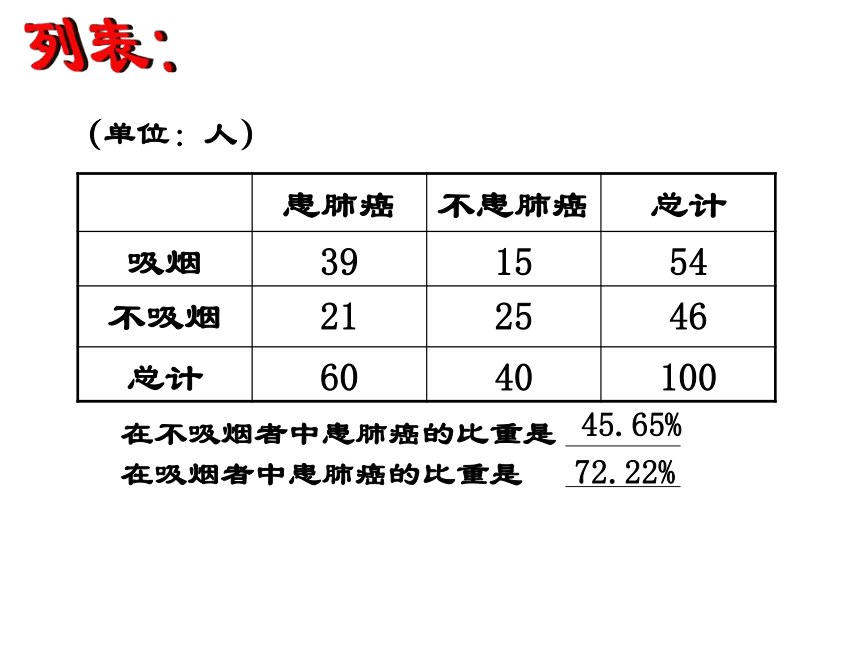
课件15张PPT。4.3列联表独立性分析案例 某医疗机构为了了解患肺癌与吸烟是否有关,进行了一次抽样调查,共调查了100个成年人,其中吸烟者54人,不吸烟者46人,调查结果是:吸烟的54人中39人患肺癌, 15人不患肺癌;不吸烟的46人中21人患肺癌,25人不患肺癌。
●根据这些数据能否断定:患肺癌与
吸烟有关?问题:列表:(单位:人)72.22%45.65%通过分析数据,得到的直观印象是吸烟和患肺癌有关,
那么事实是否真的如此呢?这需要用统计观点来考察这个问题。 现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,为此先假设 H0:吸烟与患肺癌没有关系把表中的数字用字母代替,得到如下用字母表示的列联表看看能够推出什么样的结论。 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22列联表 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22 如果“吸烟与患肺癌没有关系”,则在吸烟者中患肺癌的比
例应该与不吸烟者中相应的比例应差不多,即因此|n11n22 -n12n21|越小,说明吸烟与患肺癌之间关系越弱;
|n11n22 -n12n21|越大,说明吸烟与患肺癌之间关系越强。 为了使不同样本容量的数据有统一的评判标准引入一个随机变量:卡方统计量 作为检验在多大程度上可以认为“两个变量有关系”的标准 。 若 H0成立,即“吸烟与患肺癌没有关系”,
则 应很小。 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n通过公式计算统计学家总结出规律:如果2×2列联表中的两个对象是独立的,令 的值与临界值3.84与6.64进行比较在H0成立的情况下,在H0成立的情况下,通过公式计算∴H0是一个小概率事件,一般不会发生。即“吸烟与患肺癌没有关系”这个假设不对。所以吸烟与患肺癌有关系。用 统计量研究这类问题的方法称为独立性检验。一般地,对于两个研究对象X和Y,X有两类
取值,即A和ā(如吸烟与不吸烟);Y也有两类
取值,即B和 (如患病与不患病)。
于是得到下列联表所示的抽样数据:2×2列联表 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22要推断“A和B有关系”,可按下面的步骤进行:(1)提出假设H0 :A和B无关;(4)查对临界值,作出判断。(2)绘制2×2列表; 由于抽样的随机性,由样本得到的推断有可能正确,也有可能错误。利用 进行独立性检验,可以对推断的正确性的概率作出估计,样本量n越大,估计越准确。(3)利用公式计算 的值
打开名案P11作业:
1、P16习题3
2、名案4.3.1反证法原理与假设检验原理反证法原理: 在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。假设检验原理:在一个已知假设下,如果一个与该假设矛盾的小概率事件发生,就推断这个假设不成立。
●根据这些数据能否断定:患肺癌与
吸烟有关?问题:列表:(单位:人)72.22%45.65%通过分析数据,得到的直观印象是吸烟和患肺癌有关,
那么事实是否真的如此呢?这需要用统计观点来考察这个问题。 现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,为此先假设 H0:吸烟与患肺癌没有关系把表中的数字用字母代替,得到如下用字母表示的列联表看看能够推出什么样的结论。 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22列联表 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22 如果“吸烟与患肺癌没有关系”,则在吸烟者中患肺癌的比
例应该与不吸烟者中相应的比例应差不多,即因此|n11n22 -n12n21|越小,说明吸烟与患肺癌之间关系越弱;
|n11n22 -n12n21|越大,说明吸烟与患肺癌之间关系越强。 为了使不同样本容量的数据有统一的评判标准引入一个随机变量:卡方统计量 作为检验在多大程度上可以认为“两个变量有关系”的标准 。 若 H0成立,即“吸烟与患肺癌没有关系”,
则 应很小。 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n通过公式计算统计学家总结出规律:如果2×2列联表中的两个对象是独立的,令 的值与临界值3.84与6.64进行比较在H0成立的情况下,在H0成立的情况下,通过公式计算∴H0是一个小概率事件,一般不会发生。即“吸烟与患肺癌没有关系”这个假设不对。所以吸烟与患肺癌有关系。用 统计量研究这类问题的方法称为独立性检验。一般地,对于两个研究对象X和Y,X有两类
取值,即A和ā(如吸烟与不吸烟);Y也有两类
取值,即B和 (如患病与不患病)。
于是得到下列联表所示的抽样数据:2×2列联表 n11 n12 n21 n22 n2+ n1+ n+1 n+2 n= n11 + n21= n12 + n22= n11 + n12 + n21 + n22 = n11 + n12= n21 + n22要推断“A和B有关系”,可按下面的步骤进行:(1)提出假设H0 :A和B无关;(4)查对临界值,作出判断。(2)绘制2×2列表; 由于抽样的随机性,由样本得到的推断有可能正确,也有可能错误。利用 进行独立性检验,可以对推断的正确性的概率作出估计,样本量n越大,估计越准确。(3)利用公式计算 的值
打开名案P11作业:
1、P16习题3
2、名案4.3.1反证法原理与假设检验原理反证法原理: 在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。假设检验原理:在一个已知假设下,如果一个与该假设矛盾的小概率事件发生,就推断这个假设不成立。
同课章节目录
