事件的独立性(福建省福州市鼓楼区)

课件16张PPT。4.2 事件的独立性4.2.1.事件的独立性（一）定义：在一定条件下可能发生也可能不发生的事件
叫随机事件。定义：在一定条件下必然要发生的事件叫必然事件。定义：在一定条件下不可能发生的事件叫不可能事件。例如:①木柴燃烧，产生热量;
②抛一石块,下落.例如:③在常温下,焊锡熔化;
④在标准大气压下，且温度低于0℃时，冰融化.例如: ⑤抛一枚硬币,正面朝上;
⑥某人射击一次,中靶.等等.
条件：木柴燃烧；结果：产生热量条件：常温下；结果：焊锡熔化条件：抛一石块；结果：下落条件：标准大气压下且温度低于0oC；结果：冰融化条件：抛一枚硬币；结果：正面朝上条件：射击一次；结果：中靶必修3复习P108概率反映了随机事件发生的可能性的大小；
必然事件的概率为1，不可能事件的概率为0．
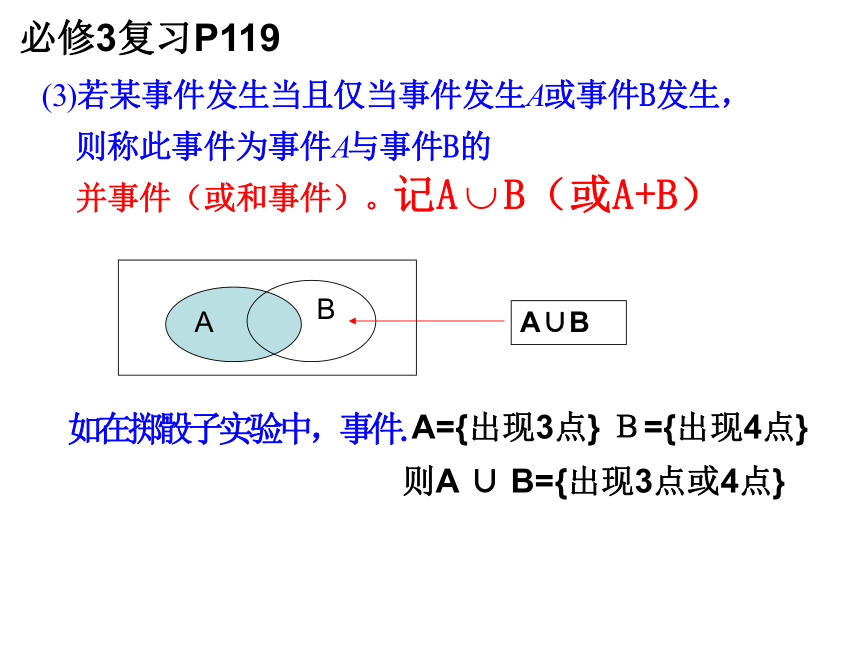
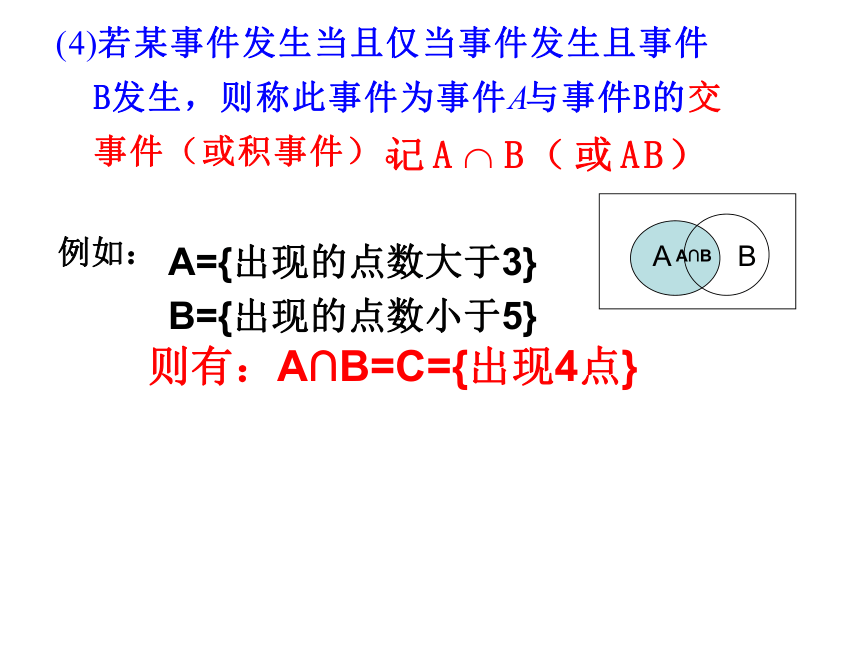
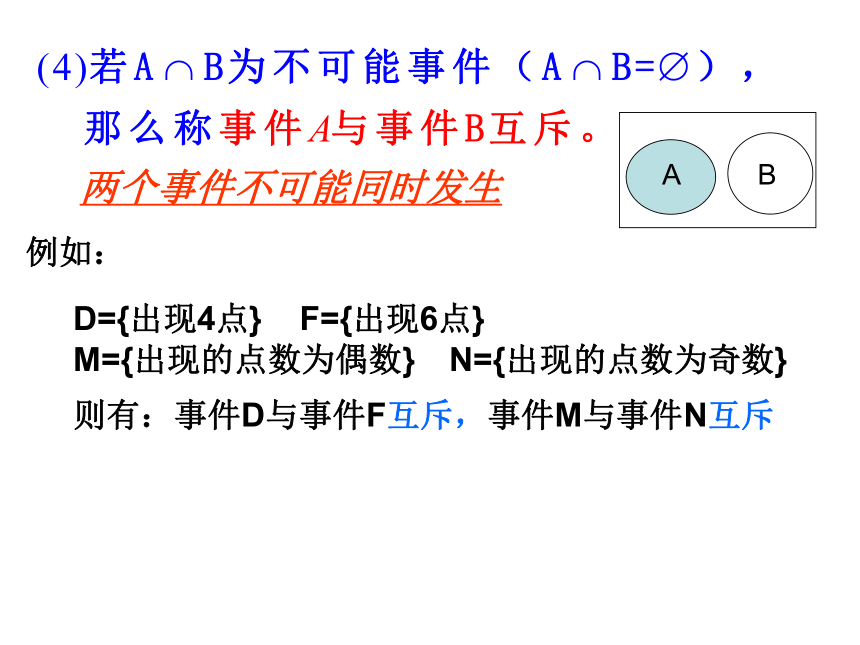
因此0?P(A)?1 A={出现3点} Ｂ={出现4点}则A ∪ B={出现3点或4点}必修3复习P119例如：A={出现的点数大于3}B={出现的点数小于5}则有：A∩B=C={出现4点}例如：D={出现4点} F={出现6点}M={出现的点数为偶数}　N={出现的点数为奇数}则有：事件D与事件F互斥，事件M与事件N互斥
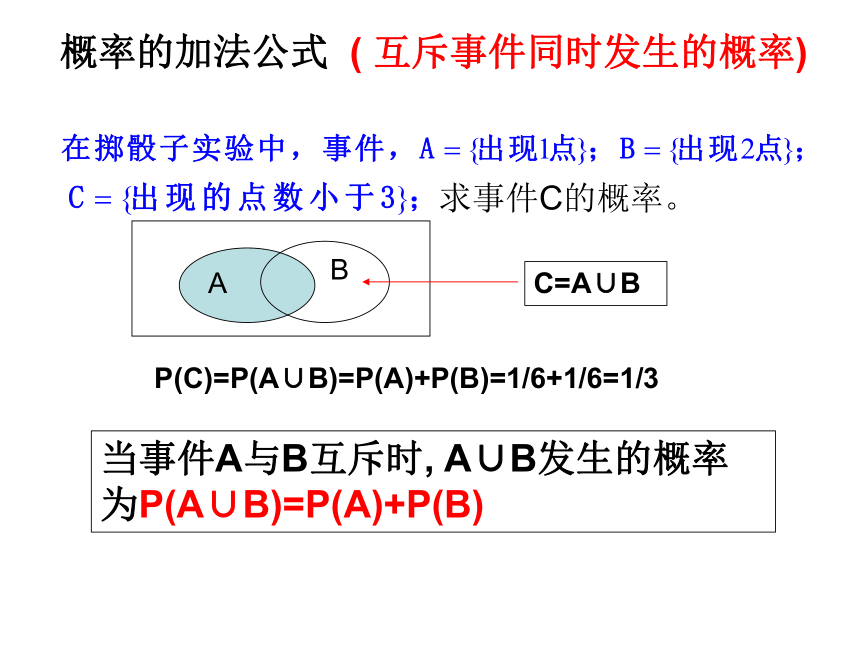
两个事件不可能同时发生概率的加法公式 ( 互斥事件同时发生的概率)当事件A与B互斥时, A∪B发生的概率为P(A∪B)=P(A)+P(B)P(C)=P(A∪B)=P(A)+P(B)=1/6+1/6=1/3求事件C的概率。 事件A与事件B互为对立事件的含义是：
这两个事件在任何一次试验中有且仅有一个发生。A={出现的点数为偶数} ā ={出现的点数为奇数}例如：则有：Ａ与ā互为对立事件如何求对立事件有一个事件发生的概率？当事件A与ā对立时, A发生的概率为
P(A)=1- P(ā)P(G) = 1- 1/2 = 1/2互斥事件与对立事件的区别与联系:
互斥事件是指事件A与事件B在一次试验中不会同时发生，
其具体包括三种不同的情形：
(1)事件A发生且事件B不发生(2)事件A不发生且事件B发生；
（3）事件A与事件B同时不发生.
而对立事件是指事件A与事件B有且仅有一个发生，其包括两种情形；
（1）事件A发生B不发生；（2）事件B发生事件A不发生，
对立事件是互斥事件的特殊情形。例如：掷一枚均匀硬币可能出现结果有：正面向上，反面
向上这2个，由于硬币是均匀的，可以认为出现这2种结果
的可能性是相等的，即可以认为出现“正面向上”的概率为
1/2 ，出现“反面向上“的概率也是1/2。又如：抛掷一个均匀的正方体玩具（它的每个面上分别标
以1、2、3、4、5、6），它落地时向上的数可能的情况是
1、2、3、4、5、6之一，即可能出现的结果有6种，由于
正方体玩具是均匀的，可以认为这6种结果出现的可能性
都相等，出现每种结果的概率都是1/6。等可能事件概率的计算方法：在一次试验中，等可能出现n个结果，组成一个集合I，
事件A包含m个结果，事件A的概率为事件I事件A独立事件的定义:
事件A(或B)是否发生对事件B(或A)发生的概率没有影响，称事件A、B独立. P(A∩B)=P(A)?P(B) 两个相互独立事件同时发生的概率，等于每个事件发生的概率的积相互独立事件概率的乘法公式：做课本P7例1、例2看课本P6-7练习:做名案：P5：1、2、3、10作业:
名案4.2.1(明天上完课后交)