人教版五年级上册数学平行四边形的面积课件(共23张PPT)
文档属性
| 名称 | 人教版五年级上册数学平行四边形的面积课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 950.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 17:56:41 | ||
图片预览





文档简介
(共23张PPT)
义务教育六年制教科书数学第九册
平行四边形的面积
教学目标
本节课我们主要来学习平行四边形的面
积,同学们要掌握平行四边形面积公式的推导
过程,能够应用平行四边形的面积公式计算
平行四边形的面积,能够解决相关的实际问
题。
想一想:
1.学校门前的花坛各是什么图形?
2.哪个花坛的面积大?
3.你会计算它们的面积吗?
用数方格的方法试一试!
一个方格代表1m ,不满一格的都按半格计算。
平行四
边形
长方形
底 高 面积
长 宽 面积
6米
4米
24平方米
6米
4米
24平方米
平行四边形 底 高 面 积
6米 4米 24平方米
长方形 长 宽 面 积
6米 4米 24平方米
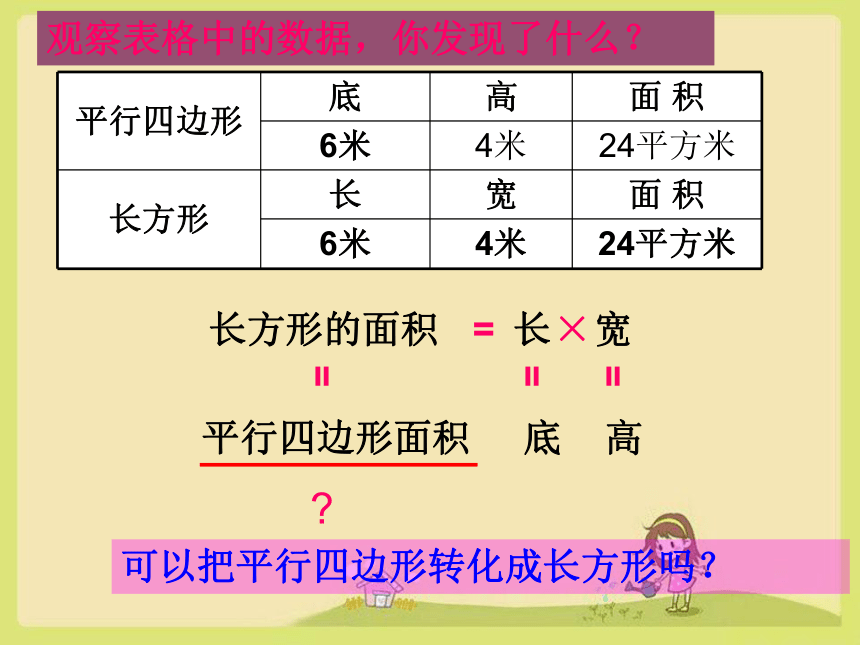
观察表格中的数据,你发现了什么?
平行四边形面积 底 高
长方形的面积 长 宽
=
=
=
=
×
可以把平行四边形转化成长方形吗?
组内互相演示把平行四边形转化成长方形转化过程,然后,思考下面的问题:
1、拼出的长方形和原来的平行四边形比,面积变了吗?
2、拼出的长方形的长和宽与原来的平行四边形的底和高有什么关系?
3、你能根据长方形面积的计算公式推导出平行四边形的面积计算公式吗?
动手验证,自主探讨
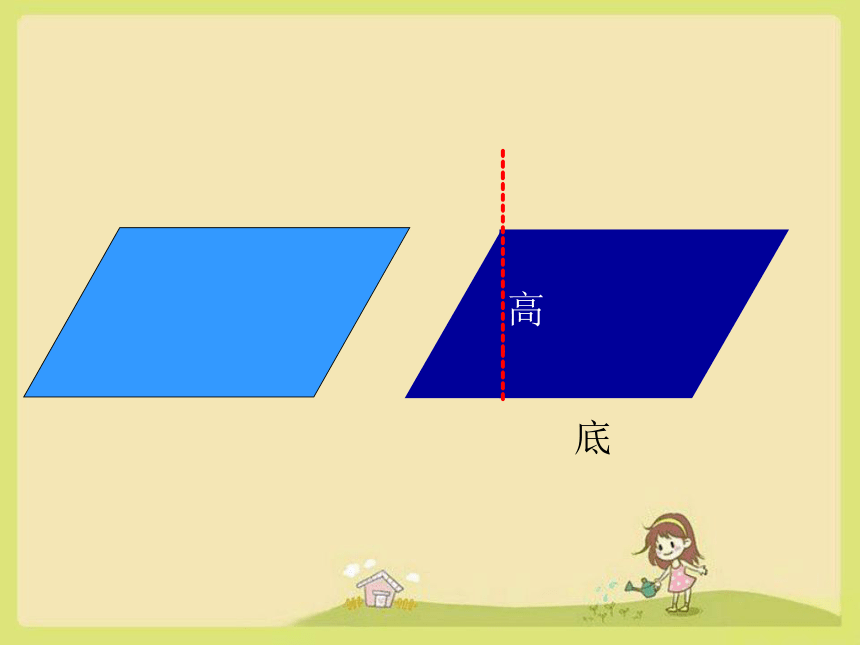
高
底
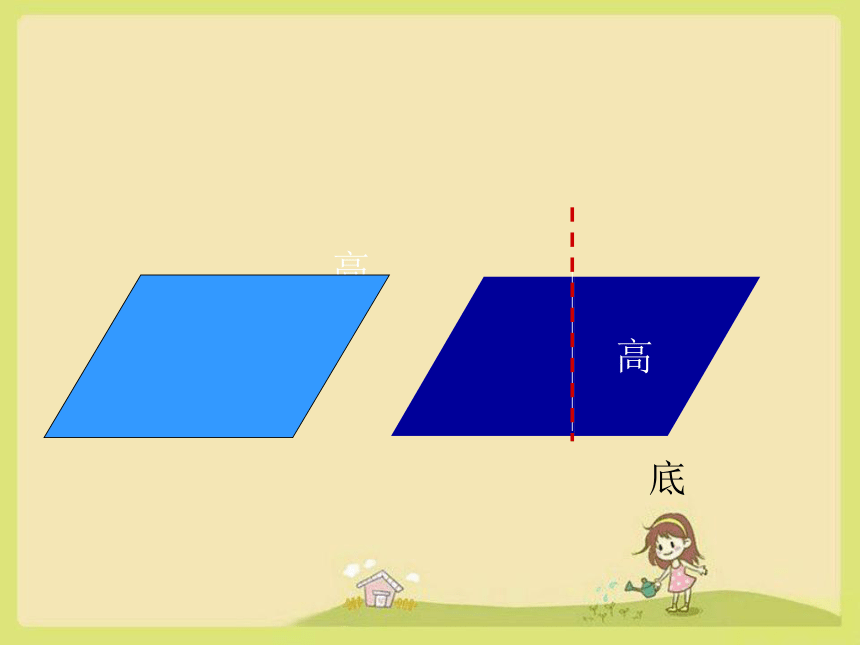
高
高
底
高
讨论:1.拼出的长方形和平行四边形比,面积变了吗
2.拼出的长方形的长与宽和原来的平行四边
形的底与高有什么关系
3.你能推导出平行四边形的面积公式吗
平行四边形转化为长方形形状变了,面积没变。
长方形的长 =平行四边形的底
长方形的宽=平行四边的高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
长方形的面积 = 长 × 宽
平行四边形的面积 =
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
S = a h
例1:一个平行四边形花坛底6米,高4米,它的面积是多少?
6米
4米
如果每平方米花45元,一共需要花多少钱?
S=ah
6×4=24(平方米)
答:它的面积是24平方米。
45×24=1080(元)
答:一共需要花1080元。
一个平行四边形的停车位底长5米,高2.5米,它的面积是多少?
5×2.5=12.5(平方米)
答:它的面积是12.5平方米
练习
2.这个平行四边形的高是多少
28m
7 m
1.求出下面各图形的面积。
3.2m
3.8m
7.8cm
6.9cm
有一块平行四边形麦田,底是250m,高是84m,共收小麦14.7吨,这块麦田有多少公顷 平均每公顷收小麦多少吨
计算这个平行四边形的面积,下面几个选择,你选哪个?为什么?
答:面积相等,因为两条平行线间的距离处处相等
两个平行四边形的底和高相等,所以面积也相等,都是 s=ah=2.5×1.4=3.5 (平方厘米)
4
想一想
?
1.4
下图中的正方形周长是32cm。你能求出平行四边形的面积吗
用木条做成一个长方形框,长18厘米,宽15厘米,(接头处忽略不计)。它的周长和面积各是多少?如果把它拉成一个平行四边形,周长和面积有变化吗?
下图中大平行四边形的面积是48cm2。A、B是上、下两边的中点。你能求出图中小平行四边形(阴影部分)的面积吗
A
B
本课小结
本节课我们主要学行四边形的面积计算,同学们要理解并掌握平行四边形面积公式的推导过程,能够解决相关的实际问题。
义务教育六年制教科书数学第九册
平行四边形的面积
教学目标
本节课我们主要来学习平行四边形的面
积,同学们要掌握平行四边形面积公式的推导
过程,能够应用平行四边形的面积公式计算
平行四边形的面积,能够解决相关的实际问
题。
想一想:
1.学校门前的花坛各是什么图形?
2.哪个花坛的面积大?
3.你会计算它们的面积吗?
用数方格的方法试一试!
一个方格代表1m ,不满一格的都按半格计算。
平行四
边形
长方形
底 高 面积
长 宽 面积
6米
4米
24平方米
6米
4米
24平方米
平行四边形 底 高 面 积
6米 4米 24平方米
长方形 长 宽 面 积
6米 4米 24平方米
观察表格中的数据,你发现了什么?
平行四边形面积 底 高
长方形的面积 长 宽
=
=
=
=
×
可以把平行四边形转化成长方形吗?
组内互相演示把平行四边形转化成长方形转化过程,然后,思考下面的问题:
1、拼出的长方形和原来的平行四边形比,面积变了吗?
2、拼出的长方形的长和宽与原来的平行四边形的底和高有什么关系?
3、你能根据长方形面积的计算公式推导出平行四边形的面积计算公式吗?
动手验证,自主探讨
高
底
高
高
底
高
讨论:1.拼出的长方形和平行四边形比,面积变了吗
2.拼出的长方形的长与宽和原来的平行四边
形的底与高有什么关系
3.你能推导出平行四边形的面积公式吗
平行四边形转化为长方形形状变了,面积没变。
长方形的长 =平行四边形的底
长方形的宽=平行四边的高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
长方形的面积 = 长 × 宽
平行四边形的面积 =
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
S = a h
例1:一个平行四边形花坛底6米,高4米,它的面积是多少?
6米
4米
如果每平方米花45元,一共需要花多少钱?
S=ah
6×4=24(平方米)
答:它的面积是24平方米。
45×24=1080(元)
答:一共需要花1080元。
一个平行四边形的停车位底长5米,高2.5米,它的面积是多少?
5×2.5=12.5(平方米)
答:它的面积是12.5平方米
练习
2.这个平行四边形的高是多少
28m
7 m
1.求出下面各图形的面积。
3.2m
3.8m
7.8cm
6.9cm
有一块平行四边形麦田,底是250m,高是84m,共收小麦14.7吨,这块麦田有多少公顷 平均每公顷收小麦多少吨
计算这个平行四边形的面积,下面几个选择,你选哪个?为什么?
答:面积相等,因为两条平行线间的距离处处相等
两个平行四边形的底和高相等,所以面积也相等,都是 s=ah=2.5×1.4=3.5 (平方厘米)
4
想一想
?
1.4
下图中的正方形周长是32cm。你能求出平行四边形的面积吗
用木条做成一个长方形框,长18厘米,宽15厘米,(接头处忽略不计)。它的周长和面积各是多少?如果把它拉成一个平行四边形,周长和面积有变化吗?
下图中大平行四边形的面积是48cm2。A、B是上、下两边的中点。你能求出图中小平行四边形(阴影部分)的面积吗
A
B
本课小结
本节课我们主要学行四边形的面积计算,同学们要理解并掌握平行四边形面积公式的推导过程,能够解决相关的实际问题。
