1.5 三角函数的应用——解直角三角形的应用(2) 导学案 2023—2024学年北师大版数学九年级下册 无答案
文档属性
| 名称 | 1.5 三角函数的应用——解直角三角形的应用(2) 导学案 2023—2024学年北师大版数学九年级下册 无答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 09:01:16 | ||
图片预览

文档简介
第5课 三角函数的应用——解直角三角形的应用(2)
课前预习
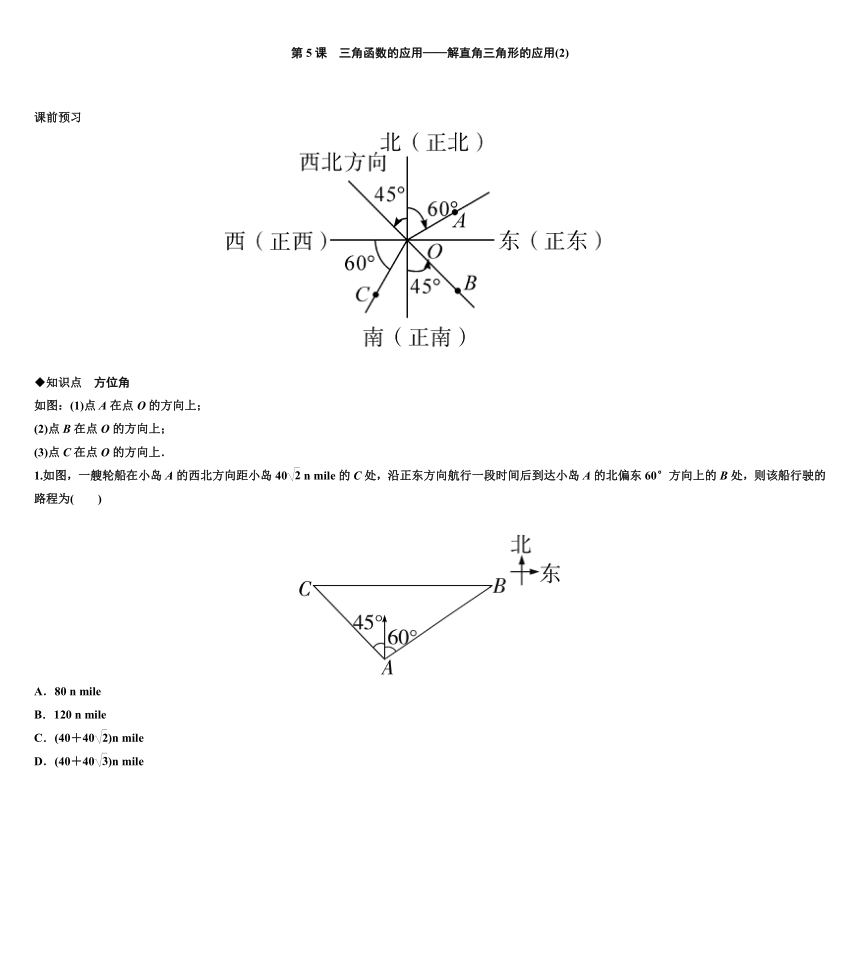
◆知识点 方位角
如图:(1)点A在点O的方向上;
(2)点B在点O的方向上;
(3)点C在点O的方向上.
1.如图,一艘轮船在小岛A的西北方向距小岛40 n mile的C处,沿正东方向航行一段时间后到达小岛A的北偏东60°方向上的B处,则该船行驶的路程为( )
A.80 n mile
B.120 n mile
C.(40+40)n mile
D.(40+40)n mile
2.如图,在一笔直的海岸线l上有相距 2 km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为km.
◆知识点 坡度与坡角
3.如图,大坝的横断面为梯形ABCD,斜坡AB的坡比i=1∶2,背水坡CD的坡比i=1∶1,若坡面CD的长度为6 m,求斜坡AB的长.
4.如图,梯形ABCD是拦水坝的横断面,斜坡CD的坡度i=1∶,∠B=60°,AB=12,AD=6,求坝底BC的长.
小结
在解决与坡度有关的问题时,一般通过作高构造直角三角形,即过上底的顶点作下底的垂线,构造直角三角形和矩形,其实质是解直角三角形.
强化训练
1.如图,游艇在湖面上以12 km/h的速度向正东方向航行,在O处时看到灯塔A在游艇北偏东60°方向上,航行1 h到达B处,此时看到灯塔A在游艇北偏西45°方向上,求此时游艇与灯塔的距离AB.(结果保留根号)
2.如图,某公园入口处有三级台阶,每级台阶高为18 cm,宽为30 cm,为方便残疾人士,拟将台阶改为斜坡.设台阶的起点为A,斜坡的起点为C,现设计斜坡BC的坡度i=2∶5,求AC的长.
3.【模型观念】如图,海平面上灯塔O方圆100 km范围内有暗礁,一艘轮船自西向东航行,在点A处测得灯塔O在北偏东60°方向上,继续航行100 km后,在点B处测得灯塔O在北偏东37°方向上.请判断,为了避免触礁,这艘轮船是否要改变航向?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
4.(教材P19)如图,某商场准备改善原有楼梯的安全性能,把倾斜角由40°减至35°,已知原楼梯长为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01 m;参考数据:sin 40°≈0.642 8,cos 40°≈0.766 0,sin 35°≈0.573 6,tan 35°≈0.700 2)
课前预习
◆知识点 方位角
如图:(1)点A在点O的方向上;
(2)点B在点O的方向上;
(3)点C在点O的方向上.
1.如图,一艘轮船在小岛A的西北方向距小岛40 n mile的C处,沿正东方向航行一段时间后到达小岛A的北偏东60°方向上的B处,则该船行驶的路程为( )
A.80 n mile
B.120 n mile
C.(40+40)n mile
D.(40+40)n mile
2.如图,在一笔直的海岸线l上有相距 2 km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为km.
◆知识点 坡度与坡角
3.如图,大坝的横断面为梯形ABCD,斜坡AB的坡比i=1∶2,背水坡CD的坡比i=1∶1,若坡面CD的长度为6 m,求斜坡AB的长.
4.如图,梯形ABCD是拦水坝的横断面,斜坡CD的坡度i=1∶,∠B=60°,AB=12,AD=6,求坝底BC的长.
小结
在解决与坡度有关的问题时,一般通过作高构造直角三角形,即过上底的顶点作下底的垂线,构造直角三角形和矩形,其实质是解直角三角形.
强化训练
1.如图,游艇在湖面上以12 km/h的速度向正东方向航行,在O处时看到灯塔A在游艇北偏东60°方向上,航行1 h到达B处,此时看到灯塔A在游艇北偏西45°方向上,求此时游艇与灯塔的距离AB.(结果保留根号)
2.如图,某公园入口处有三级台阶,每级台阶高为18 cm,宽为30 cm,为方便残疾人士,拟将台阶改为斜坡.设台阶的起点为A,斜坡的起点为C,现设计斜坡BC的坡度i=2∶5,求AC的长.
3.【模型观念】如图,海平面上灯塔O方圆100 km范围内有暗礁,一艘轮船自西向东航行,在点A处测得灯塔O在北偏东60°方向上,继续航行100 km后,在点B处测得灯塔O在北偏东37°方向上.请判断,为了避免触礁,这艘轮船是否要改变航向?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
4.(教材P19)如图,某商场准备改善原有楼梯的安全性能,把倾斜角由40°减至35°,已知原楼梯长为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01 m;参考数据:sin 40°≈0.642 8,cos 40°≈0.766 0,sin 35°≈0.573 6,tan 35°≈0.700 2)
