北京市2023-2024学年九年级下学期4月验收数学试卷(无答案)
文档属性
| 名称 | 北京市2023-2024学年九年级下学期4月验收数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 472.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 23:04:02 | ||
图片预览




文档简介
2023-2024学年度第二学期北京市4月验收九年级数学试卷
考生须知:
1. 本试卷分为第I卷和第II卷,第I卷共2页,第II卷共6页.
2. 本试卷满分100分,考试时间120分钟.
3. 在试卷(包括第I卷和第II卷)密封线内准确填写学校、班级、姓名、学号.
4. 考试结束,将试卷及答题纸一并交回监考老师.
第一部分 选择题
一、选择题(共16分,每题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1. 下图是某几何体的三视图,该几何体是( )
A. 圆柱 B. 圆锥 C. 长方体 D. 三棱柱
2. 实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
3. 如图,直线,,则的大小是( )
A. B. C. D.
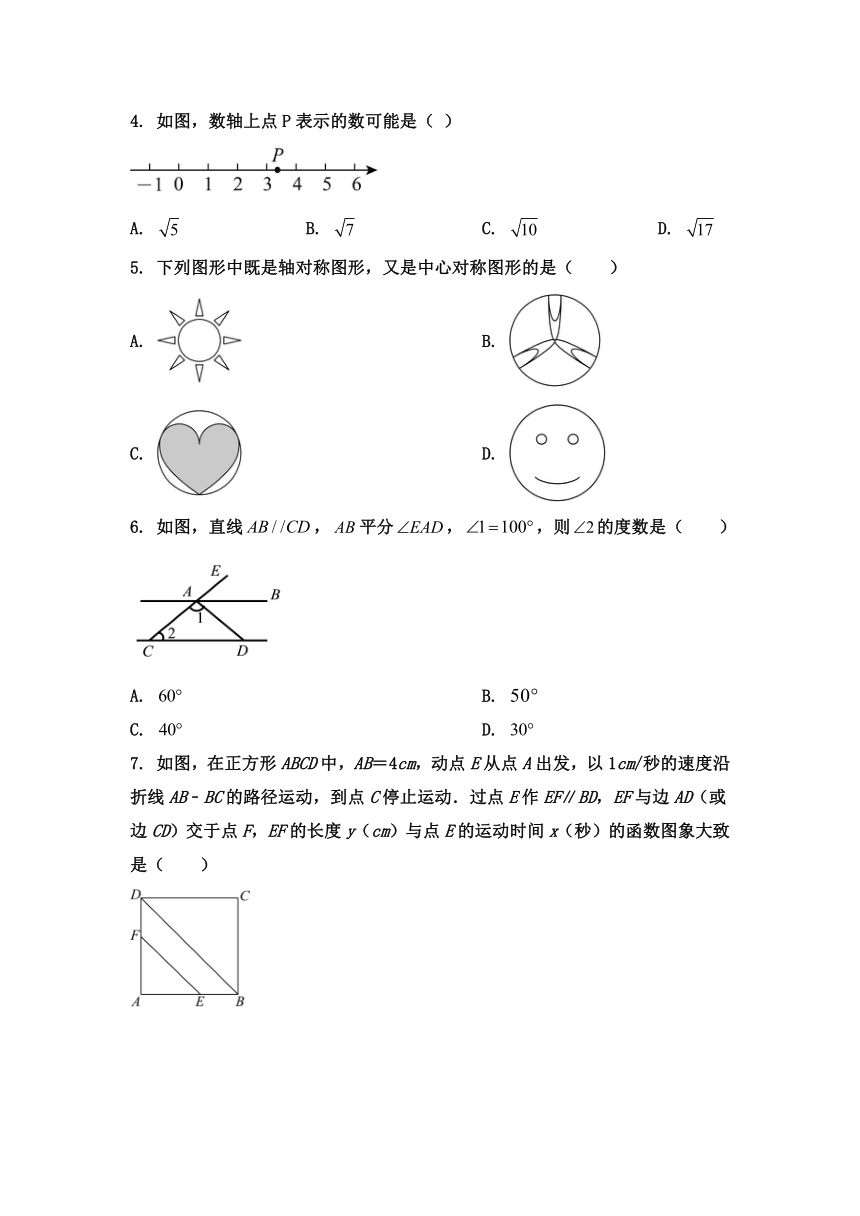
4. 如图,数轴上点P表示的数可能是( )
A. B. C. D.
5. 下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
6. 如图,直线,平分,,则的度数是( )
A. B.
C. D.
7. 如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB﹣BC的路径运动,到点C停止运动.过点E作EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是( )
A. B. C.D.
8. 如图1,矩形的一条边长为x,周长的一半为y.定义为这个矩形的坐标.如图2,在平面直角坐标系中,直线,将第一象限划分成4个区域.已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中.
则下面叙述中正确的是( )
A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
二、填空题(共8个小题,每小题2分,共16分)
9. 若在实数范围内有意义,则实数x的取值范围是___________.
10. 分解因式:xy―x=_____________.
11. 若n为整数,且,则n值为________________.
12. 分式方程的解________.
13. 中国古代数学著作《算法统宗》记载了这样一个题目:九百九十文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:九百九十文钱共买一千个苦果和甜果,其中四文钱可买苦果七个,十一文钱可买甜果九个.问苦、甜果各几个?设苦果x个,甜果y个;则可列方程为_____.
14. 如图,在△ABC中,AB=AC,∠A=40°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则的度数是_______°.
15.一组学生春游,预计共需要费用120元,后来又有2人参加进来,总费用不变,于是每人可少摊3元,若设原来这组学生人数为x,那么可列方程为 .
16.如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在⊙O上,边AB、AC分别交⊙O于D、E两点,点B是的中点,则∠ABE= .
三、解答题(共68分,17~20题,每题5分,21题6分,22~23题,每题5分,24~26题,每题6分,
27~28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
17.(5分)计算:.
18.(5分)解不等式组,并将解集在数轴上表示出来.
19. 下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线l和直线l外一点A
求作:直线AP,使得AP∥l
作法:如图
①在直线l上任取一点B(AB与l不垂直),以点A为圆心,AB为半径作圆,与直线l交于点C.
②连接AC,AB,延长BA到点D;
③作∠DAC的平分线AP.
所以直线AP就是所求作的直线
根据小星同学设计尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB (填推理的依据)
∵∠DAC是△ABC的外角,
∴∠DAC=∠ABC+∠ACB (填推理的依据)
∴∠DAC=2∠ABC
∵AP平分∠DAC,
∴∠DAC=2∠DAP
∴∠DAP=∠ABC
∴AP∥l (填推理的依据)
20. 已知关于一元二次方程.
(1)如果该方程有两个不相等的实数根,求的取值范围.
(2)在(1)的条件下,当该方程的两个根都是整数,求正整数的值.
21. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G, CD=AE.
(1)求证: CG=EG.
(2)已知BC=13, CD=5,连结ED,求△EDC 的面积.
22. 在平面直角坐标系中,一次函数的图象平行于直线,且经过点.
(1)求这个一次函数的表达式;
(2)当时,对于的每一个值,一次函数的值都大于一次函数的值,直接写出的取值范围.
23. 门头沟区深挖区域绿水青山教育资源,以区域山水和历史人文资源为素材,开展跨学科实践活动.某校为调研学生的学习成效.举办“跨学科综合实践活动”成果作品比赛.十名评委对每组同学的参赛作品进行现场打分.对参加比赛的甲,乙,丙三组同学参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲.乙两组同学参赛作品得分的折线图:
b.丙组同学参赛作品得分:
9 4 9 9 10 9 10 8 8 10
c.甲,乙,丙三组同学参赛作品得分的平均数、众数、中位数如下:
平均数 众数 中位数
甲组 8.6 9 9
乙组 8.6 8.5
丙组 8.6 9
根据以上信息,回答下列问题:
(1)表中_____,______;
(2)在参加比赛的小组中,如果某组同学参赛作品得分的个数据的方差越小,则认为评委对该组同学参赛作品的评价越一致.据此推断:在甲,乙两组同学中,评委对______组同学的参赛作品评价更一致(填“甲”或“乙”)
(3)如果每组同学最后得分为去掉十名评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该组同学的参赛作品越优秀.据此推断:在甲,乙,丙三组同学中,参赛作品最优秀的是______组同学(填“甲”或“乙”或“丙”).
24. 如图,为的直径,为弦,射线与相切于点A,过点O作交于点D,连接.
(1)求证:是的切线;
(2)过点B作交的延长线于点E,连接交于点F.若,,求的长.
25. 数学活动课上,老师提出一个探究问题:
制作一个体积为,底面为正方形的长方体包装盒,当底面边长为多少时,需要的材料最省(底面边长不超过3dm,且不考虑接缝).
某小组经讨论得出:材料最省,就是尽可能使得长方体的表面积最小.
下面是他们的探究过程,请补充完整:
(1)设长方体包装盒的底面边长为,表面积为.
可以用含的代数式表示长方体的高为.
根据长方体的表面积公式:长方体表面积.
得到与的关系式:___________________();
(2)列出与的几组对应值:
… 0.5 10 1.5 2.0 2.5 3.0
… 80.5 42.0 31.2 28.5 31.3
(说明:表格中相关数值精确到十分位)
表中_____________.
(3)在下面的平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象:
(4)结合画出的函数图象,解决问题:
长方体包装盒的底面边长约为_________dm时,需要的材料最省;当长方体包装盒表面积为时,底面边长约为____________dm.
26. 在平面直角坐标系中,抛物线的顶点为点,且,
(1)若,
点到轴的距离为_____________;
已知点,,若抛物线与线段有且只有一个公共点,求取值范围;
(2)已知点到轴的距离为,此抛物线与直线的两个交点分别为,,其中,若点在此抛物线上,当时,总满足,求的值和的取值范围.
27. 如图,在每一个四边形ABCD中,均有AD//BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.
(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为__________;
(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;
(3)如图③,在四边形ABCD边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时
cos∠BPC值;若不存在,请说明理由.
28.(7分)如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
考生须知:
1. 本试卷分为第I卷和第II卷,第I卷共2页,第II卷共6页.
2. 本试卷满分100分,考试时间120分钟.
3. 在试卷(包括第I卷和第II卷)密封线内准确填写学校、班级、姓名、学号.
4. 考试结束,将试卷及答题纸一并交回监考老师.
第一部分 选择题
一、选择题(共16分,每题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1. 下图是某几何体的三视图,该几何体是( )
A. 圆柱 B. 圆锥 C. 长方体 D. 三棱柱
2. 实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
3. 如图,直线,,则的大小是( )
A. B. C. D.
4. 如图,数轴上点P表示的数可能是( )
A. B. C. D.
5. 下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
6. 如图,直线,平分,,则的度数是( )
A. B.
C. D.
7. 如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB﹣BC的路径运动,到点C停止运动.过点E作EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是( )
A. B. C.D.
8. 如图1,矩形的一条边长为x,周长的一半为y.定义为这个矩形的坐标.如图2,在平面直角坐标系中,直线,将第一象限划分成4个区域.已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中.
则下面叙述中正确的是( )
A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
二、填空题(共8个小题,每小题2分,共16分)
9. 若在实数范围内有意义,则实数x的取值范围是___________.
10. 分解因式:xy―x=_____________.
11. 若n为整数,且,则n值为________________.
12. 分式方程的解________.
13. 中国古代数学著作《算法统宗》记载了这样一个题目:九百九十文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:九百九十文钱共买一千个苦果和甜果,其中四文钱可买苦果七个,十一文钱可买甜果九个.问苦、甜果各几个?设苦果x个,甜果y个;则可列方程为_____.
14. 如图,在△ABC中,AB=AC,∠A=40°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则的度数是_______°.
15.一组学生春游,预计共需要费用120元,后来又有2人参加进来,总费用不变,于是每人可少摊3元,若设原来这组学生人数为x,那么可列方程为 .
16.如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在⊙O上,边AB、AC分别交⊙O于D、E两点,点B是的中点,则∠ABE= .
三、解答题(共68分,17~20题,每题5分,21题6分,22~23题,每题5分,24~26题,每题6分,
27~28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
17.(5分)计算:.
18.(5分)解不等式组,并将解集在数轴上表示出来.
19. 下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线l和直线l外一点A
求作:直线AP,使得AP∥l
作法:如图
①在直线l上任取一点B(AB与l不垂直),以点A为圆心,AB为半径作圆,与直线l交于点C.
②连接AC,AB,延长BA到点D;
③作∠DAC的平分线AP.
所以直线AP就是所求作的直线
根据小星同学设计尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB (填推理的依据)
∵∠DAC是△ABC的外角,
∴∠DAC=∠ABC+∠ACB (填推理的依据)
∴∠DAC=2∠ABC
∵AP平分∠DAC,
∴∠DAC=2∠DAP
∴∠DAP=∠ABC
∴AP∥l (填推理的依据)
20. 已知关于一元二次方程.
(1)如果该方程有两个不相等的实数根,求的取值范围.
(2)在(1)的条件下,当该方程的两个根都是整数,求正整数的值.
21. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G, CD=AE.
(1)求证: CG=EG.
(2)已知BC=13, CD=5,连结ED,求△EDC 的面积.
22. 在平面直角坐标系中,一次函数的图象平行于直线,且经过点.
(1)求这个一次函数的表达式;
(2)当时,对于的每一个值,一次函数的值都大于一次函数的值,直接写出的取值范围.
23. 门头沟区深挖区域绿水青山教育资源,以区域山水和历史人文资源为素材,开展跨学科实践活动.某校为调研学生的学习成效.举办“跨学科综合实践活动”成果作品比赛.十名评委对每组同学的参赛作品进行现场打分.对参加比赛的甲,乙,丙三组同学参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲.乙两组同学参赛作品得分的折线图:
b.丙组同学参赛作品得分:
9 4 9 9 10 9 10 8 8 10
c.甲,乙,丙三组同学参赛作品得分的平均数、众数、中位数如下:
平均数 众数 中位数
甲组 8.6 9 9
乙组 8.6 8.5
丙组 8.6 9
根据以上信息,回答下列问题:
(1)表中_____,______;
(2)在参加比赛的小组中,如果某组同学参赛作品得分的个数据的方差越小,则认为评委对该组同学参赛作品的评价越一致.据此推断:在甲,乙两组同学中,评委对______组同学的参赛作品评价更一致(填“甲”或“乙”)
(3)如果每组同学最后得分为去掉十名评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该组同学的参赛作品越优秀.据此推断:在甲,乙,丙三组同学中,参赛作品最优秀的是______组同学(填“甲”或“乙”或“丙”).
24. 如图,为的直径,为弦,射线与相切于点A,过点O作交于点D,连接.
(1)求证:是的切线;
(2)过点B作交的延长线于点E,连接交于点F.若,,求的长.
25. 数学活动课上,老师提出一个探究问题:
制作一个体积为,底面为正方形的长方体包装盒,当底面边长为多少时,需要的材料最省(底面边长不超过3dm,且不考虑接缝).
某小组经讨论得出:材料最省,就是尽可能使得长方体的表面积最小.
下面是他们的探究过程,请补充完整:
(1)设长方体包装盒的底面边长为,表面积为.
可以用含的代数式表示长方体的高为.
根据长方体的表面积公式:长方体表面积.
得到与的关系式:___________________();
(2)列出与的几组对应值:
… 0.5 10 1.5 2.0 2.5 3.0
… 80.5 42.0 31.2 28.5 31.3
(说明:表格中相关数值精确到十分位)
表中_____________.
(3)在下面的平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象:
(4)结合画出的函数图象,解决问题:
长方体包装盒的底面边长约为_________dm时,需要的材料最省;当长方体包装盒表面积为时,底面边长约为____________dm.
26. 在平面直角坐标系中,抛物线的顶点为点,且,
(1)若,
点到轴的距离为_____________;
已知点,,若抛物线与线段有且只有一个公共点,求取值范围;
(2)已知点到轴的距离为,此抛物线与直线的两个交点分别为,,其中,若点在此抛物线上,当时,总满足,求的值和的取值范围.
27. 如图,在每一个四边形ABCD中,均有AD//BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.
(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为__________;
(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;
(3)如图③,在四边形ABCD边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时
cos∠BPC值;若不存在,请说明理由.
28.(7分)如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
同课章节目录
