2.1 等式性质与不等式性质(2个课时) 课件(共5张PPT)
文档属性
| 名称 | 2.1 等式性质与不等式性质(2个课时) 课件(共5张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 13:58:56 | ||
图片预览











文档简介
(共59张PPT)
第2章一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【输入学校全称】
(第1课时)
1
新课导入
思考1:
日常生活中,存在着大量的不等关系
那么,在数学的世界,我们如何表示不等关系?
思考
左图交通标志中,
分别是最低限速 和 最高限速 标志
“最低、最高、限”表示的含义
2
探究新知
新知【1】
不等关系与不等式
我们用数学符号“≠”、“>”、“<”、“≥”、“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些符号的式子,叫做不等式。
记作:
f(x)≠g(x)
f(x)>g(x)
f(x)≥g(x)
f(x)f(x)≤g(x)
练习
用不等式来表示不等关系:
v1 ≤120 km/h v2 ≥60 km/h
速度不超过120km/h,速度不低于60km/h.
语言
描述
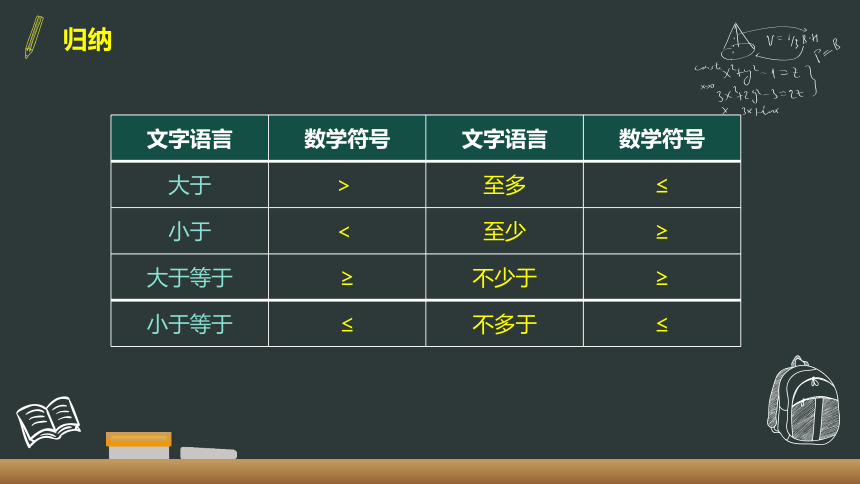
归纳
文字语言 数学符号 文字语言 数学符号
大于 > 至多 ≤
小于 < 至少 ≥
大于等于 ≥ 不少于 ≥
小于等于 ≤ 不多于 ≤
探究
这是某酸奶的质量检查规定.
1
用数学关系如何反映表中所述信息?
f≥2.5%,并且p≥2.3%,是这样表达吗?
脂肪含量(f) 蛋白质含量(p)
不少于2.5% 不少于2.3%
新知【2】
用不等式组来表示不等关系
一般的,我们将多个不等式用”{”合并展现,表示一组不等关系,数学中称做不等式组。
上页探究中,
某酸奶的质量检查规定,
可以用如下不等式组表示:
f≥2.5%
p≥2.3%
练习
某钢铁厂要把长度为4000 mm的钢管截成500 mm和600 mm两种,按照生产的要求,600 mm钢管的数量不能超过500 mm钢管的3倍.试写出满足上述所有不等关系的不等式.
【分析】
应先设出相应变量,找出其中的不等关系,即
①两种钢管的总长度不能超过4 000 mm;
②截得600 mm钢管的数量不能超过500 mm钢管数量的3倍;③两种钢管的数量都不能为负.
于是可列不等式组表示上述不等关系.
练习
【解析】 设截得500 mm的钢管x根,截得600 mm的钢管y根,
依题意,可得不等式组:
考虑到实际问题,x, y应为正整数
归纳
用不等式(组)表示实际问题中不等关系的步骤:
①审题.通读题目,分清楚已知量和待求量,设出待求量.找出体现不等关系的关键词:“至少”“至多”“不少于”“不多于”“超过”“不超过”等.
②列不等式组:分析题意,找出已知量和待求量之间的约束条件,将各约束条件用不等式表示.
探究
比较数的大小
2
(1)数轴上的任意两点中,右边点对应的实数比左边点对应的实数______.
(2)对于任意两个实数a和b,
如果a-b是正数,那么a ______ b;
如果a-b是负数,那么a ______ b;
如果a-b等于零,那么a ______ b.
大
>
<
=
探究
比较式子的大小
3
已知x<y<0,比较(x2+y2)(x-y)与(x2-y2)(x+y)的大小.
∵ x<y<0,xy>0,x-y<0,
∴ (x2+y2)(x-y)-(x2-y2)(x+y)=-2xy(x-y)>0,
∴ (x2+y2)(x-y)>(x2-y2)(x+y).
【解析】
新知【3】
比较两个实数(或代数式)大小
(1) 作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形(因式分解、通分、配方等);
(3)判断差的符号:结合变形的结果及题设条件判断差的符号;
(4)作出结论.这种比较大小的方法通常称为作差比较法.其思维过程:作差→变形→判断符号→结论,其中变形是判断符号的前提.
练习
设M=x 2,N=-x-1,则M 与N 的大小关系是 ( )
A.M>N B.M=N
C.M【解析】 M-N=x 2+x+1=(x+)2+ >0,
∴M>N,故选A.
A
练习
比较+ +1与2(x+y-1)的大小.
x2+y2+1-2(x+y-1)
=x2-2x+1+y2-2y+2
=(x-1)2+(y-1)2+1>0,
∴ x2+y2+1>2(x+y-1).
【解析】
3
随堂检测
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
检测
【答案】 D
检测
2. 若A=+3与B=+2,则A与B的大小关系是( )
A.A>B B.A【解析】 由于A-B=+3->0,
所以A>B, 故选A.
【答案】 A
检测
3.已知甲、乙两种食物的维生素A,B含量如下表:
设用x kg的甲种食物与y kg的乙种食物配成混合食物,并使混合食物内至少含有56 000单位的维生素A和63 000 单位的维生素B.试用不等式组表示x,y所满足的不等关系.
食 物 甲 乙
维生素A/(单位/kg) 600 700
维生素B/(单位/kg) 800 400
检测
检测
4.将一个三边长度分别为5,12,13的三角形的各边都缩短x,构成一个钝角三角形,试用不等式(组)表示x应满足的不等关系.
检测
检测
4
课堂总结
总结
1.不等式与不等关系
(1)不等式的定义所含的两个要点.
①不等符号>,<,≥,≤或≠.
②所表示的关系是不等关系.
(2)不等式中的文字语言与符号语言之间的转换.
文字语言 大于 大于 等于 小于 小于 等于 至多 至少 不少于 不多于
符号语言 > ≥ < ≤ ≤ ≥ ≥ ≤
总结
2.比较两个实数a、b大小的依据
文字语言 符号表示
如果a>b,那么a-b是 正数 ; 如果ab __a-b>0___
aa=b __a-b=0___
第2章一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【输入学校全称】
(第2课时)
1
新课导入
回顾:
类比等式的性质,你能猜想出不等式的性质,并加以证明吗?
思考
你能回忆起等式的基本性质吗?
性质1 若a=b, 则 b=a;
性质2 若a=b, b=c, 则a=c;
性质3 若a=b, 则a±c=b±c;
性质4 若a=b, 则ac=bc;
性质5 若a=b, c≠0, 则=
2
探究新知
新知【1】
不等式的性质
① 对称性
文字语言 不等式两边互换后,再将不等号改变方向,所得不等式与原不等式等价
符号语言 a>b b作用 写出与原不等式等价且异向的不等式
证明: ∵ a>b, ∴ a-b>0.
由正数的相反数是负数, 得-(a-b)<0.
即b-a<0, ∴ b同理可证, 如果bb.
练习
与m≥(n-2)2等价的是( ).
A.m<(n-2)2 B.(n-2)2≥m
C.(n-2)2≤m D.(n-2)2C
新知【2】
不等式的性质
② 传递性
文字语言 如果第一个量大于第二个量,第二个量大于第三个量,那么第一个量大于第三个量
符号语言 a>b , b>c a>c
变形 a≥b , b≥c a≥c;
aa≤b , b≤c a≤c
作用 比较大小或证明不等式
你能证明这个性质吗?
新知【3】
不等式的性质
③ 加法法则
文字语言 不等式的两边都加上同一个实数,所得的不等式与原不等式同向.
符号语言 a>b a+c > b+c
变形 aa≤b a+c ≤ b+c
a≥b a+c ≥ b+c
作用 不等式的移项,等价变形
证明: ∵ (a+c)-(b+c)=a-b>0,
∴ a+c>b+c.
新知【4】
不等式的性质
④ 乘法法则
文字语言 不等式的两边都乘同一个正数时,不等号的方向不变;
都乘同一个负数时,不等号的方向一定要改变.
符号语言 a>b, c>0 ac>bc a>b, c<0 ac变形 a≥b, c>0 ac≥bc a≥b, c<0 ac≤bc
a0 acbc
a≤b, c>0 ac≤bc a≤b, c<0 ac≥bc
作用 不等式的同解变形
证明: ac-bc=(a-b)c.∵a>b,∴a-b>0.根据同号相乘得正,异号相乘得负,
得当c>0时,(a-b)c>0,即ac>bc;当c<0时,(a-b)c<0,即ac归纳
1. 该性质不能逆推,如ac>bc a>b.
2. ac>bc a>b,c>0或a3. 不等式两边仅能同乘(或除以)一个符号确定的非零实数.
④ 乘法法则
新知【5】
不等式的性质
⑤加法单调性
文字语言 两个同向不等式相加,所得不等式与原不等式同向.
符号语言 a>b, c>d a+c > b+d
变形 aa≥b, c≥d a+c ≥ b+d
a≤b, c≤d a+c ≤ b+d
作用 由已知同向不等式推出其他不等式
归纳
⑤加法单调性
1. 此性质可以推广到任意有限个同向不等式的两边分别相加,即两个或两个以上的同向不等式两边分别相加,所得不等式与原不等式同向.
2. 两个同向不等式只能两边同时分别相加,而不能两边同时分别相减.
3. 该性质不能逆推,如a+c>b+d a>b,c>d.
新知【6】
不等式的性质
⑥乘法单调性
文字语言 两边都是正数的两个同向不等式相乘,所得不等式与原不等式同向.
符号语言 a>b>0, c>d>0 ac > bd
作用 两个不等式相乘的变形
证明: ∵ a>b>0,c>0,
∴ ac>bc.
∵ c>d>0, b>0,
∴ bc>bd.
∴ ac>bd.
归纳
1. 这一性质可以推广到任意有限个两边都是正数的同向不等式两边分别相乘,这就是说,两个或更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向.
2.a>b>0,cabd.
3.该性质不能逆推,如ac>bd a>b,c>d.
⑥乘法单调性
新知【7】
不等式的性质
⑦正值不等式可乘方
文字语言 当不等式的两边都是正数时,
不等式两边同时乘方所得的不等式与原不等式同向.
符号语言 a>b>0 an>bn (n∈N*,且n>1)
作用 不等式两边的乘方变形
概念延伸:
当n 是正奇数时, 由a>b 可得an>bn
新知【8】
不等式的性质
⑧正值不等式可开方
文字语言 当不等式的两边都是正数时,
不等式两边同时开方所得的不等式与原不等式同向.
符号语言 a>b>0 > (n∈N*,且n>1)
作用 不等式两边的开方变形
练习
1. 若a>b>0 ,则下列不等式总成立的是 ( )
C
练习
2. 有以下四个条件:
(1) b>0>a; (2) 0>a>b;
(3) a>0>b; (4) a>b>0.
其中能使
成立的有________个.
3
练习
利用不等式性质判断不等式是否成立
利用不等式性质判断不等式是否成立
练习
归纳
运用不等式的性质判断.要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质.
应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则.
可用特殊值法判断. 取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算.
练习
利用不等式性质求取值范围
利用不等式性质求取值范围
练习
3
随堂检测
1.已知aA.a-cbd
C. < D.ad>bc
检测
【答案】 B
检测
检测
【答案】 D
检测
3.设2【答案】 5< 2a-b <8
检测
4
课堂总结
总结
不等式的性质
1 a>b b2 a>b,b>c a>c 传递性
3 a>b a+c>b+c 可加性 可逆
4 a>b,c>0 ac>bc ;a>b,c<0 ac5 a>b, c>d a+c > b+d 同向可加性 同向
6 a>b>0, c>d>0 ac > bd 同向同正可乘性 同向,同正
7 a>b>0 an>bn , > (n∈N*,且n>1) 可乘方/可开方性 n>1自然数
运用不等式的性质
1不等式性质的求证,2用不等式性质证明不等式,3用不等式性质求取值范围
第2章一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【输入学校全称】
(第1课时)
1
新课导入
思考1:
日常生活中,存在着大量的不等关系
那么,在数学的世界,我们如何表示不等关系?
思考
左图交通标志中,
分别是最低限速 和 最高限速 标志
“最低、最高、限”表示的含义
2
探究新知
新知【1】
不等关系与不等式
我们用数学符号“≠”、“>”、“<”、“≥”、“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些符号的式子,叫做不等式。
记作:
f(x)≠g(x)
f(x)>g(x)
f(x)≥g(x)
f(x)
练习
用不等式来表示不等关系:
v1 ≤120 km/h v2 ≥60 km/h
速度不超过120km/h,速度不低于60km/h.
语言
描述
归纳
文字语言 数学符号 文字语言 数学符号
大于 > 至多 ≤
小于 < 至少 ≥
大于等于 ≥ 不少于 ≥
小于等于 ≤ 不多于 ≤
探究
这是某酸奶的质量检查规定.
1
用数学关系如何反映表中所述信息?
f≥2.5%,并且p≥2.3%,是这样表达吗?
脂肪含量(f) 蛋白质含量(p)
不少于2.5% 不少于2.3%
新知【2】
用不等式组来表示不等关系
一般的,我们将多个不等式用”{”合并展现,表示一组不等关系,数学中称做不等式组。
上页探究中,
某酸奶的质量检查规定,
可以用如下不等式组表示:
f≥2.5%
p≥2.3%
练习
某钢铁厂要把长度为4000 mm的钢管截成500 mm和600 mm两种,按照生产的要求,600 mm钢管的数量不能超过500 mm钢管的3倍.试写出满足上述所有不等关系的不等式.
【分析】
应先设出相应变量,找出其中的不等关系,即
①两种钢管的总长度不能超过4 000 mm;
②截得600 mm钢管的数量不能超过500 mm钢管数量的3倍;③两种钢管的数量都不能为负.
于是可列不等式组表示上述不等关系.
练习
【解析】 设截得500 mm的钢管x根,截得600 mm的钢管y根,
依题意,可得不等式组:
考虑到实际问题,x, y应为正整数
归纳
用不等式(组)表示实际问题中不等关系的步骤:
①审题.通读题目,分清楚已知量和待求量,设出待求量.找出体现不等关系的关键词:“至少”“至多”“不少于”“不多于”“超过”“不超过”等.
②列不等式组:分析题意,找出已知量和待求量之间的约束条件,将各约束条件用不等式表示.
探究
比较数的大小
2
(1)数轴上的任意两点中,右边点对应的实数比左边点对应的实数______.
(2)对于任意两个实数a和b,
如果a-b是正数,那么a ______ b;
如果a-b是负数,那么a ______ b;
如果a-b等于零,那么a ______ b.
大
>
<
=
探究
比较式子的大小
3
已知x<y<0,比较(x2+y2)(x-y)与(x2-y2)(x+y)的大小.
∵ x<y<0,xy>0,x-y<0,
∴ (x2+y2)(x-y)-(x2-y2)(x+y)=-2xy(x-y)>0,
∴ (x2+y2)(x-y)>(x2-y2)(x+y).
【解析】
新知【3】
比较两个实数(或代数式)大小
(1) 作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形(因式分解、通分、配方等);
(3)判断差的符号:结合变形的结果及题设条件判断差的符号;
(4)作出结论.这种比较大小的方法通常称为作差比较法.其思维过程:作差→变形→判断符号→结论,其中变形是判断符号的前提.
练习
设M=x 2,N=-x-1,则M 与N 的大小关系是 ( )
A.M>N B.M=N
C.M
∴M>N,故选A.
A
练习
比较+ +1与2(x+y-1)的大小.
x2+y2+1-2(x+y-1)
=x2-2x+1+y2-2y+2
=(x-1)2+(y-1)2+1>0,
∴ x2+y2+1>2(x+y-1).
【解析】
3
随堂检测
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
检测
【答案】 D
检测
2. 若A=+3与B=+2,则A与B的大小关系是( )
A.A>B B.A【解析】 由于A-B=+3->0,
所以A>B, 故选A.
【答案】 A
检测
3.已知甲、乙两种食物的维生素A,B含量如下表:
设用x kg的甲种食物与y kg的乙种食物配成混合食物,并使混合食物内至少含有56 000单位的维生素A和63 000 单位的维生素B.试用不等式组表示x,y所满足的不等关系.
食 物 甲 乙
维生素A/(单位/kg) 600 700
维生素B/(单位/kg) 800 400
检测
检测
4.将一个三边长度分别为5,12,13的三角形的各边都缩短x,构成一个钝角三角形,试用不等式(组)表示x应满足的不等关系.
检测
检测
4
课堂总结
总结
1.不等式与不等关系
(1)不等式的定义所含的两个要点.
①不等符号>,<,≥,≤或≠.
②所表示的关系是不等关系.
(2)不等式中的文字语言与符号语言之间的转换.
文字语言 大于 大于 等于 小于 小于 等于 至多 至少 不少于 不多于
符号语言 > ≥ < ≤ ≤ ≥ ≥ ≤
总结
2.比较两个实数a、b大小的依据
文字语言 符号表示
如果a>b,那么a-b是 正数 ; 如果a
aa=b __a-b=0___
第2章一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【输入学校全称】
(第2课时)
1
新课导入
回顾:
类比等式的性质,你能猜想出不等式的性质,并加以证明吗?
思考
你能回忆起等式的基本性质吗?
性质1 若a=b, 则 b=a;
性质2 若a=b, b=c, 则a=c;
性质3 若a=b, 则a±c=b±c;
性质4 若a=b, 则ac=bc;
性质5 若a=b, c≠0, 则=
2
探究新知
新知【1】
不等式的性质
① 对称性
文字语言 不等式两边互换后,再将不等号改变方向,所得不等式与原不等式等价
符号语言 a>b b
证明: ∵ a>b, ∴ a-b>0.
由正数的相反数是负数, 得-(a-b)<0.
即b-a<0, ∴ b
练习
与m≥(n-2)2等价的是( ).
A.m<(n-2)2 B.(n-2)2≥m
C.(n-2)2≤m D.(n-2)2
新知【2】
不等式的性质
② 传递性
文字语言 如果第一个量大于第二个量,第二个量大于第三个量,那么第一个量大于第三个量
符号语言 a>b , b>c a>c
变形 a≥b , b≥c a≥c;
aa≤b , b≤c a≤c
作用 比较大小或证明不等式
你能证明这个性质吗?
新知【3】
不等式的性质
③ 加法法则
文字语言 不等式的两边都加上同一个实数,所得的不等式与原不等式同向.
符号语言 a>b a+c > b+c
变形 aa≤b a+c ≤ b+c
a≥b a+c ≥ b+c
作用 不等式的移项,等价变形
证明: ∵ (a+c)-(b+c)=a-b>0,
∴ a+c>b+c.
新知【4】
不等式的性质
④ 乘法法则
文字语言 不等式的两边都乘同一个正数时,不等号的方向不变;
都乘同一个负数时,不等号的方向一定要改变.
符号语言 a>b, c>0 ac>bc a>b, c<0 ac
a
a≤b, c>0 ac≤bc a≤b, c<0 ac≥bc
作用 不等式的同解变形
证明: ac-bc=(a-b)c.∵a>b,∴a-b>0.根据同号相乘得正,异号相乘得负,
得当c>0时,(a-b)c>0,即ac>bc;当c<0时,(a-b)c<0,即ac
1. 该性质不能逆推,如ac>bc a>b.
2. ac>bc a>b,c>0或a
④ 乘法法则
新知【5】
不等式的性质
⑤加法单调性
文字语言 两个同向不等式相加,所得不等式与原不等式同向.
符号语言 a>b, c>d a+c > b+d
变形 a
a≤b, c≤d a+c ≤ b+d
作用 由已知同向不等式推出其他不等式
归纳
⑤加法单调性
1. 此性质可以推广到任意有限个同向不等式的两边分别相加,即两个或两个以上的同向不等式两边分别相加,所得不等式与原不等式同向.
2. 两个同向不等式只能两边同时分别相加,而不能两边同时分别相减.
3. 该性质不能逆推,如a+c>b+d a>b,c>d.
新知【6】
不等式的性质
⑥乘法单调性
文字语言 两边都是正数的两个同向不等式相乘,所得不等式与原不等式同向.
符号语言 a>b>0, c>d>0 ac > bd
作用 两个不等式相乘的变形
证明: ∵ a>b>0,c>0,
∴ ac>bc.
∵ c>d>0, b>0,
∴ bc>bd.
∴ ac>bd.
归纳
1. 这一性质可以推广到任意有限个两边都是正数的同向不等式两边分别相乘,这就是说,两个或更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向.
2.a>b>0,c
3.该性质不能逆推,如ac>bd a>b,c>d.
⑥乘法单调性
新知【7】
不等式的性质
⑦正值不等式可乘方
文字语言 当不等式的两边都是正数时,
不等式两边同时乘方所得的不等式与原不等式同向.
符号语言 a>b>0 an>bn (n∈N*,且n>1)
作用 不等式两边的乘方变形
概念延伸:
当n 是正奇数时, 由a>b 可得an>bn
新知【8】
不等式的性质
⑧正值不等式可开方
文字语言 当不等式的两边都是正数时,
不等式两边同时开方所得的不等式与原不等式同向.
符号语言 a>b>0 > (n∈N*,且n>1)
作用 不等式两边的开方变形
练习
1. 若a>b>0 ,则下列不等式总成立的是 ( )
C
练习
2. 有以下四个条件:
(1) b>0>a; (2) 0>a>b;
(3) a>0>b; (4) a>b>0.
其中能使
成立的有________个.
3
练习
利用不等式性质判断不等式是否成立
利用不等式性质判断不等式是否成立
练习
归纳
运用不等式的性质判断.要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质.
应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则.
可用特殊值法判断. 取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算.
练习
利用不等式性质求取值范围
利用不等式性质求取值范围
练习
3
随堂检测
1.已知a
C. < D.ad>bc
检测
【答案】 B
检测
检测
【答案】 D
检测
3.设2
检测
4
课堂总结
总结
不等式的性质
1 a>b b2 a>b,b>c a>c 传递性
3 a>b a+c>b+c 可加性 可逆
4 a>b,c>0 ac>bc ;a>b,c<0 ac
6 a>b>0, c>d>0 ac > bd 同向同正可乘性 同向,同正
7 a>b>0 an>bn , > (n∈N*,且n>1) 可乘方/可开方性 n>1自然数
运用不等式的性质
1不等式性质的求证,2用不等式性质证明不等式,3用不等式性质求取值范围
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
