山东省菏泽第一中学人民路校区2024届高三下学期3月月考数学试题(含解析)
文档属性
| 名称 | 山东省菏泽第一中学人民路校区2024届高三下学期3月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 15:01:22 | ||
图片预览




文档简介
菏泽一中人民路校区2024届高三3月份月考
数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.抛掷两枚质地均匀的骰子,设事件“第一枚出现奇数点”,事件“第二枚出现偶数点”,则与的关系是( )
A. 互斥 B. 互为对立 C. 相互独立 D. 相等
2.双曲线的渐近线方程为,则( )
A. B. C. D.
3.已知平面向量,满足,若,则与的夹角是
( )
A. B. C. D.
4.已知各项均为正数的等比数列的前项和为,且满足,,成等差数列,则( )
A. B. C. D.
5.攒尖是中国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称为攒尖通常有圆形攒尖,三角攒尖,四角攒尖,八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑如图所示的建筑屋顶是圆形攒尖,可近似看作一个圆锥,已知其轴截面是底边长为,顶角为的等腰三角形,则该屋顶的面积约为( )
A. B. C. D.
6.黄山是中国著名的旅游胜地,有许多值得打卡的旅游景点,其中包括黄山风景区,齐云山,宏村,徽州古城等甲,乙,丙人准备前往黄山风景区,齐云山,宏村,徽州古城这个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
A. 种 B. 种 C. 种 D. 种
7.已知双曲线的左,右焦点分别为,,过作一条渐近线的垂线,垂足为,延长与另一条渐近线交于点,若为坐标原点,则双曲线的离心率为( )
A. B. C. D.
8.已知实数,分别满足,,且,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.有一组样本数据,,,,,的平均数是,方差是,极差为,则下列判断正确的是
( )
A. 若,,,,,的平均数是,则
B. 若,,,,,的极差是,则
C. 若方差,则
D. 若,则第百分位数是
10.已知直三棱柱中,且,直线与底面所成角的正弦值为,则
( )
A. 线段上存在点,使得
B. 线段上存在点,使得平面平面
C. 直三棱柱的体积为
D. 点到平面的距离为
11.已知函数的定义域为,且,,为偶函数,则
( )
A. B. 为奇函数 C. D.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知集合,,则 .
13.在中,角,,的对边分别为,,,,,边上的高等于,则的面积是 , .
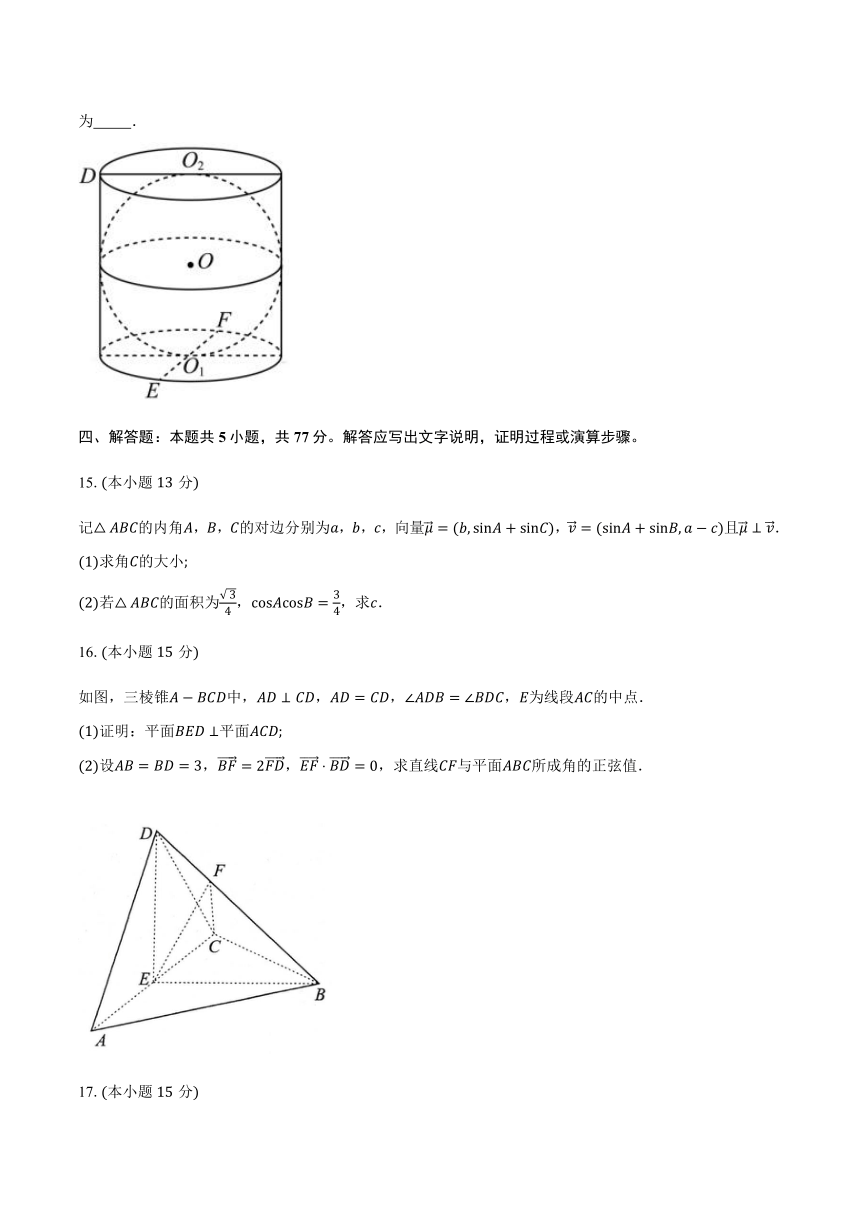
14.如图,球内切于圆柱,圆柱的高为,为底面圆的一条直径,为圆上任意一点,则平面截球所得截面面积最小值为 若为球面和圆柱侧面交线上的一点,则周长的取值范围为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角,,的对边分别为,,,向量,且.
求角的大小
若的面积为,,求.
16.本小题分
如图,三棱锥中,,,,为线段的中点.
证明:平面平面
设,,,求直线与平面所成角的正弦值.
17.本小题分
学校食堂为了减少排队时间,从开学第天起,每餐只推出即点即取的米饭套餐和面食套餐某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前天选择了米饭套餐,则第天选择米饭套餐的概率为若他前天选择了面食套餐,则第天选择米饭套餐的概率为已知他开学第天中午选择米饭套餐的概率为.
求该同学开学第天中午选择米饭套餐的概率
记该同学开学第天中午选择米饭套餐的概率为证明:当时,.
18.本小题分
已知为抛物线上的动点,为圆上的动点,若的最小值为.
求的值
若动点在轴上方,过作圆的两条切线分别交抛物线于另外两点,,且满足,求直线的方程.
19.本小题分
帕德近似是法国数学家亨利帕德发明的用有理多项式近似特定函数的方法给定两个正整数,,函数在处的阶帕德近似定义为:
,且满足:
,,,,
注:,,,,
已知函数.
求函数在处的阶帕德近似,并求的近似数精确到
在的条件下:
(ⅰ)求证:
(ⅱ)若恒成立,求实数的取值范围.
菏泽一中人民路校区2024届高三月考数学试题
答案和解析
1.【答案】
【解析】【分析】
本题考查互斥,对立,独立事件的定义,属于基础题.
根据定义判断两个事件是否相互独立,利用定义法,满足即独立.
【解答】
解:由题可知,抛掷两枚质地均匀的骰子,第一枚和第二枚出现点数的分类情况如下,
奇数,奇数,奇数,偶数,偶数,奇数,偶数,偶数,
事件“第一枚出现奇数点”,
事件“第二枚出现偶数点”,
两个事件不相等,排除,
,所以不是互斥事件,排除,,
选项,事件“第一枚出现奇数点”,,
事件“第二枚出现偶数点”,,
事件“第一枚出现奇数点,第二枚出现偶数点”,,
满足,
所以事件和事件是相互独立事件,
故选:.
2.【答案】
【解析】略
3.【答案】
【解析】【分析】
本题考查了向量夹角公式,向量垂直的充要条件,属于基础题.
根据条件可得出,然后即可求出的值,从而得出答案.
【解答】解:,
,
,
,
又,
与的夹角为.
故选:.
4.【答案】
【解析】【分析】
本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.
设各项均为正数的等比数列的公比为,由,,成等差数列,可得,化为,解得,再利用求和公式即可得出.
【解答】
解:设各项均为正数的等比数列的公比为,
满足,,成等差数列,
,,
,.
解得.
则.
故选C.
5.【答案】
【解析】【分析】
本题主要考查锥体的几何性质以及侧面积求法,空间想象能力等知识,属于基础题.
由题意分别求得锥体的底面圆的半径和母线,然后计算其侧面积即可.
【解答】
解:作出该圆锥截面如图,
由已知可知,该圆形攒尖的底面圆半径,
母线,
侧面积.
故选C.
6.【答案】
【解析】【分析】
本题考查计数原理以及组合的应用,属于中档题.
依题意分三步:分别计算甲,乙,丙每人的不同的选择方法,然后利用分步乘法计数原理计算即可.
【解答】
解:依题意分三步:
第一步,甲的不同的选择有种;
第二步,乙的不同的选择也有种;
第三步,丙的不同的选择有种;
因此,根据分步乘法计数原理,得不同的选择有种
故选A.
7.【答案】
【解析】【分析】
本题考查双曲线的相关知识.双曲线的离心率的求法,考查转化思想以及计算能力,属于中档题.
利用已知条件求出点坐标,求出点到渐近线的距离,结合可以得到点到渐近线的距离为,进而利用点到直线的距离公式求出与的关系,然后求解双曲线的离心率.
【解答】
解:由题意知,双曲线的两条渐近线方程分别为,,
过点且与渐近线垂直的直线方程为,
联立,可解得,
点到渐近线的距离
因为,所以点到渐近线的距离为,
即即,所以,即双曲线的离心率为,故选D.
8.【答案】
【解析】【分析】
本题考查应用导数判断函数的单调性,利用单调性比较大小,属于中档题.
构造函数,先求证,得,再构造函数,利用导数求得,即可比较大小.
【解答】
解:由,,得,,
设,则,
所以当时,,单调递减,
当时,,单调递增,
所以,即,
同理可证,
所以,
当时,可得,即,
设,则,
所以当时,,单调递减,
当时,,单调递增,
所以,即,
整理得,即,所以.
故选C.
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】【分析】
本题主要考查函数的定义域,一元二次不等式的解法,集合的运算,属于基础题.
由定义域可得,由一元二次不等式的解法可得,利用交集、补集运算求解即可.
【解答】
解:由题,
所以.
13.【答案】
【解析】略
14.【答案】
【解析】【分析】
本题主要考查的是圆柱的结构特征,截面问题,函数的值域,多面体和旋转体上的最短距离,属于难题.
过点在平面内作,垂足为点,分析可知当平面时,截面圆的半径最小,求出截面圆的半径,结合圆的面积公式可求平面截得球的截面面积最小值利设在底面的射影为,设令,则,其中,可得出,利用平方法和二次函数的基本性质求出的取值范围,可得周长的取值范围.
【解答】
解:过点在平面内作,垂足为,如下图
易知,,
由勾股定理可得,则由题可得,
设到平面的距离为,平面截得球的截面圆的半径为,
因为,当平面,取最大值,即,所以,
所以平面截得球的截面面积最小值为.
由题可知,点在过球心与圆柱的底面平行的截面圆上,设在底面射影为,
则,,
由勾股定理可得,令,则,其中,
所以,
所以,
因此,所以周长的取值范围为.
故填:,
15.【答案】解:由得,
即,化简得,
由余弦定理得:,,
所以,
由题意得,则,
由得,
因为,所以,
所以.
【解析】本题考查向量垂直的坐标表示,正余弦定理,三角形面积公式的应用,属于中档题.
由得,然后利用余弦定理得,即可;
由题意得,然后利用,得到,即可.
16.【答案】解:因为,为线段的中点,所以
因为,,,
所以,故AB.
又为线段的中点,所以.
结合,所以平面
又平面,因此平面平面.
取的中点,连接,,
因为为中位线,所以,
又,所以.
因为,为的中点,所以.
又,所以平面,所以,
因为,为的中点,所以,
又,所以平面.
以为坐标原点,分别以、、所在的
直线为、、轴设,,
则,,,
,,
由,解得.
所以
又平面的法向量.
因此直线与平面所成角的正弦值.
【解析】略
17.【答案】解:设“第天选择米饭套餐”,则“第天选择面食套餐”,
根据题意,,,,
由全概率公式,得
设“第天选择米饭套餐”,
则,,,,
由全概率公式,得,
即,,
,是以为首项,为公比的等比数列
可得,
当为大于的奇数时,
当为正偶数时,,
综上所述:当时,.
【解析】本题主要考查了数列的递推关系的应用,还考查了全概率公式的应用,等比数列的定义的应用,属于中档题.
由已知结合全概率公式即可求解;
由已知结合全概率公式及等比数列的定义即可求出的通项公式,分类讨论即可证明.
18.【答案】解:设,的最小值为,即的最小值为,
则
当时,,;
设,,,直线的斜率,
直线的方程为:,
即,化简得,
则,即,
同理,
则,是方程的两根,
所以,则直线的斜率,
,平分,则,.
,解得,则.
且,,
故AB中点为,
直线的方程为
即.
【解析】本题主要考查了抛物线的概念,性质,直线与抛物线的位置关系,两点间距离公式,直线的斜率,点斜式方程,两条直线垂直的条件,属于较难题.
由的最小值为,得的最小值为,设 ,,由两点间距离公式可得,可得,求解即可;
设,,,求出直线的方程,即,由点到直线的距离公式,化简可得,同理,则,是方程的两根,得出,求出直线的斜率,由题意,,由两条直线垂直的条件,解得,进而求此直线的斜率及中点,即可求出结果.
19.【答案】解:由题可知函数在处的阶帕德近似,,,
由得,所以,
则,又由得,所以,
由得,所以,
.
令,
因为
所以在及上均单调递减.
当,,即,而
所以,即,
当,,即,而
所以,即
由所以不等式恒成立
由得在上恒成立
令,且,所以是的极大值点,
又,故,则,
当时,,
所以
当时,,,则,故在上单调递增,
所以当时,
当时,
令,因为,所以在上单调递减,
所以又因为在上
故当时,
综上,当时,恒成立.
【解析】本题考查导数的综合应用,考查新定义问题,考查分类讨论思想,属于难题.
先写出阶帕德近似,然后求导得到,,令得,所以,求导得到求解即可;
令,,求导得到判断在及上均单调递减,分类讨论当,当,求解即可;
由已知令,且,所以是的极大值点,求导得到,故,,得到之后写出,然后求导判断单调性证明即可.
数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.抛掷两枚质地均匀的骰子,设事件“第一枚出现奇数点”,事件“第二枚出现偶数点”,则与的关系是( )
A. 互斥 B. 互为对立 C. 相互独立 D. 相等
2.双曲线的渐近线方程为,则( )
A. B. C. D.
3.已知平面向量,满足,若,则与的夹角是
( )
A. B. C. D.
4.已知各项均为正数的等比数列的前项和为,且满足,,成等差数列,则( )
A. B. C. D.
5.攒尖是中国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称为攒尖通常有圆形攒尖,三角攒尖,四角攒尖,八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑如图所示的建筑屋顶是圆形攒尖,可近似看作一个圆锥,已知其轴截面是底边长为,顶角为的等腰三角形,则该屋顶的面积约为( )
A. B. C. D.
6.黄山是中国著名的旅游胜地,有许多值得打卡的旅游景点,其中包括黄山风景区,齐云山,宏村,徽州古城等甲,乙,丙人准备前往黄山风景区,齐云山,宏村,徽州古城这个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
A. 种 B. 种 C. 种 D. 种
7.已知双曲线的左,右焦点分别为,,过作一条渐近线的垂线,垂足为,延长与另一条渐近线交于点,若为坐标原点,则双曲线的离心率为( )
A. B. C. D.
8.已知实数,分别满足,,且,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.有一组样本数据,,,,,的平均数是,方差是,极差为,则下列判断正确的是
( )
A. 若,,,,,的平均数是,则
B. 若,,,,,的极差是,则
C. 若方差,则
D. 若,则第百分位数是
10.已知直三棱柱中,且,直线与底面所成角的正弦值为,则
( )
A. 线段上存在点,使得
B. 线段上存在点,使得平面平面
C. 直三棱柱的体积为
D. 点到平面的距离为
11.已知函数的定义域为,且,,为偶函数,则
( )
A. B. 为奇函数 C. D.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知集合,,则 .
13.在中,角,,的对边分别为,,,,,边上的高等于,则的面积是 , .
14.如图,球内切于圆柱,圆柱的高为,为底面圆的一条直径,为圆上任意一点,则平面截球所得截面面积最小值为 若为球面和圆柱侧面交线上的一点,则周长的取值范围为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角,,的对边分别为,,,向量,且.
求角的大小
若的面积为,,求.
16.本小题分
如图,三棱锥中,,,,为线段的中点.
证明:平面平面
设,,,求直线与平面所成角的正弦值.
17.本小题分
学校食堂为了减少排队时间,从开学第天起,每餐只推出即点即取的米饭套餐和面食套餐某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前天选择了米饭套餐,则第天选择米饭套餐的概率为若他前天选择了面食套餐,则第天选择米饭套餐的概率为已知他开学第天中午选择米饭套餐的概率为.
求该同学开学第天中午选择米饭套餐的概率
记该同学开学第天中午选择米饭套餐的概率为证明:当时,.
18.本小题分
已知为抛物线上的动点,为圆上的动点,若的最小值为.
求的值
若动点在轴上方,过作圆的两条切线分别交抛物线于另外两点,,且满足,求直线的方程.
19.本小题分
帕德近似是法国数学家亨利帕德发明的用有理多项式近似特定函数的方法给定两个正整数,,函数在处的阶帕德近似定义为:
,且满足:
,,,,
注:,,,,
已知函数.
求函数在处的阶帕德近似,并求的近似数精确到
在的条件下:
(ⅰ)求证:
(ⅱ)若恒成立,求实数的取值范围.
菏泽一中人民路校区2024届高三月考数学试题
答案和解析
1.【答案】
【解析】【分析】
本题考查互斥,对立,独立事件的定义,属于基础题.
根据定义判断两个事件是否相互独立,利用定义法,满足即独立.
【解答】
解:由题可知,抛掷两枚质地均匀的骰子,第一枚和第二枚出现点数的分类情况如下,
奇数,奇数,奇数,偶数,偶数,奇数,偶数,偶数,
事件“第一枚出现奇数点”,
事件“第二枚出现偶数点”,
两个事件不相等,排除,
,所以不是互斥事件,排除,,
选项,事件“第一枚出现奇数点”,,
事件“第二枚出现偶数点”,,
事件“第一枚出现奇数点,第二枚出现偶数点”,,
满足,
所以事件和事件是相互独立事件,
故选:.
2.【答案】
【解析】略
3.【答案】
【解析】【分析】
本题考查了向量夹角公式,向量垂直的充要条件,属于基础题.
根据条件可得出,然后即可求出的值,从而得出答案.
【解答】解:,
,
,
,
又,
与的夹角为.
故选:.
4.【答案】
【解析】【分析】
本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.
设各项均为正数的等比数列的公比为,由,,成等差数列,可得,化为,解得,再利用求和公式即可得出.
【解答】
解:设各项均为正数的等比数列的公比为,
满足,,成等差数列,
,,
,.
解得.
则.
故选C.
5.【答案】
【解析】【分析】
本题主要考查锥体的几何性质以及侧面积求法,空间想象能力等知识,属于基础题.
由题意分别求得锥体的底面圆的半径和母线,然后计算其侧面积即可.
【解答】
解:作出该圆锥截面如图,
由已知可知,该圆形攒尖的底面圆半径,
母线,
侧面积.
故选C.
6.【答案】
【解析】【分析】
本题考查计数原理以及组合的应用,属于中档题.
依题意分三步:分别计算甲,乙,丙每人的不同的选择方法,然后利用分步乘法计数原理计算即可.
【解答】
解:依题意分三步:
第一步,甲的不同的选择有种;
第二步,乙的不同的选择也有种;
第三步,丙的不同的选择有种;
因此,根据分步乘法计数原理,得不同的选择有种
故选A.
7.【答案】
【解析】【分析】
本题考查双曲线的相关知识.双曲线的离心率的求法,考查转化思想以及计算能力,属于中档题.
利用已知条件求出点坐标,求出点到渐近线的距离,结合可以得到点到渐近线的距离为,进而利用点到直线的距离公式求出与的关系,然后求解双曲线的离心率.
【解答】
解:由题意知,双曲线的两条渐近线方程分别为,,
过点且与渐近线垂直的直线方程为,
联立,可解得,
点到渐近线的距离
因为,所以点到渐近线的距离为,
即即,所以,即双曲线的离心率为,故选D.
8.【答案】
【解析】【分析】
本题考查应用导数判断函数的单调性,利用单调性比较大小,属于中档题.
构造函数,先求证,得,再构造函数,利用导数求得,即可比较大小.
【解答】
解:由,,得,,
设,则,
所以当时,,单调递减,
当时,,单调递增,
所以,即,
同理可证,
所以,
当时,可得,即,
设,则,
所以当时,,单调递减,
当时,,单调递增,
所以,即,
整理得,即,所以.
故选C.
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】【分析】
本题主要考查函数的定义域,一元二次不等式的解法,集合的运算,属于基础题.
由定义域可得,由一元二次不等式的解法可得,利用交集、补集运算求解即可.
【解答】
解:由题,
所以.
13.【答案】
【解析】略
14.【答案】
【解析】【分析】
本题主要考查的是圆柱的结构特征,截面问题,函数的值域,多面体和旋转体上的最短距离,属于难题.
过点在平面内作,垂足为点,分析可知当平面时,截面圆的半径最小,求出截面圆的半径,结合圆的面积公式可求平面截得球的截面面积最小值利设在底面的射影为,设令,则,其中,可得出,利用平方法和二次函数的基本性质求出的取值范围,可得周长的取值范围.
【解答】
解:过点在平面内作,垂足为,如下图
易知,,
由勾股定理可得,则由题可得,
设到平面的距离为,平面截得球的截面圆的半径为,
因为,当平面,取最大值,即,所以,
所以平面截得球的截面面积最小值为.
由题可知,点在过球心与圆柱的底面平行的截面圆上,设在底面射影为,
则,,
由勾股定理可得,令,则,其中,
所以,
所以,
因此,所以周长的取值范围为.
故填:,
15.【答案】解:由得,
即,化简得,
由余弦定理得:,,
所以,
由题意得,则,
由得,
因为,所以,
所以.
【解析】本题考查向量垂直的坐标表示,正余弦定理,三角形面积公式的应用,属于中档题.
由得,然后利用余弦定理得,即可;
由题意得,然后利用,得到,即可.
16.【答案】解:因为,为线段的中点,所以
因为,,,
所以,故AB.
又为线段的中点,所以.
结合,所以平面
又平面,因此平面平面.
取的中点,连接,,
因为为中位线,所以,
又,所以.
因为,为的中点,所以.
又,所以平面,所以,
因为,为的中点,所以,
又,所以平面.
以为坐标原点,分别以、、所在的
直线为、、轴设,,
则,,,
,,
由,解得.
所以
又平面的法向量.
因此直线与平面所成角的正弦值.
【解析】略
17.【答案】解:设“第天选择米饭套餐”,则“第天选择面食套餐”,
根据题意,,,,
由全概率公式,得
设“第天选择米饭套餐”,
则,,,,
由全概率公式,得,
即,,
,是以为首项,为公比的等比数列
可得,
当为大于的奇数时,
当为正偶数时,,
综上所述:当时,.
【解析】本题主要考查了数列的递推关系的应用,还考查了全概率公式的应用,等比数列的定义的应用,属于中档题.
由已知结合全概率公式即可求解;
由已知结合全概率公式及等比数列的定义即可求出的通项公式,分类讨论即可证明.
18.【答案】解:设,的最小值为,即的最小值为,
则
当时,,;
设,,,直线的斜率,
直线的方程为:,
即,化简得,
则,即,
同理,
则,是方程的两根,
所以,则直线的斜率,
,平分,则,.
,解得,则.
且,,
故AB中点为,
直线的方程为
即.
【解析】本题主要考查了抛物线的概念,性质,直线与抛物线的位置关系,两点间距离公式,直线的斜率,点斜式方程,两条直线垂直的条件,属于较难题.
由的最小值为,得的最小值为,设 ,,由两点间距离公式可得,可得,求解即可;
设,,,求出直线的方程,即,由点到直线的距离公式,化简可得,同理,则,是方程的两根,得出,求出直线的斜率,由题意,,由两条直线垂直的条件,解得,进而求此直线的斜率及中点,即可求出结果.
19.【答案】解:由题可知函数在处的阶帕德近似,,,
由得,所以,
则,又由得,所以,
由得,所以,
.
令,
因为
所以在及上均单调递减.
当,,即,而
所以,即,
当,,即,而
所以,即
由所以不等式恒成立
由得在上恒成立
令,且,所以是的极大值点,
又,故,则,
当时,,
所以
当时,,,则,故在上单调递增,
所以当时,
当时,
令,因为,所以在上单调递减,
所以又因为在上
故当时,
综上,当时,恒成立.
【解析】本题考查导数的综合应用,考查新定义问题,考查分类讨论思想,属于难题.
先写出阶帕德近似,然后求导得到,,令得,所以,求导得到求解即可;
令,,求导得到判断在及上均单调递减,分类讨论当,当,求解即可;
由已知令,且,所以是的极大值点,求导得到,故,,得到之后写出,然后求导判断单调性证明即可.
同课章节目录
