人教版六年级下册数学圆柱表面积2(课件)(共41张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆柱表面积2(课件)(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 19:27:16 | ||
图片预览



文档简介
(共41张PPT)
圆柱的表面积
学前准备
独立思考
合作探究
学习体会
自我测试
拓展延伸
请同学们拿出圆柱来看一看,想一想圆柱的表面积包括哪几部分,然后告诉大家。
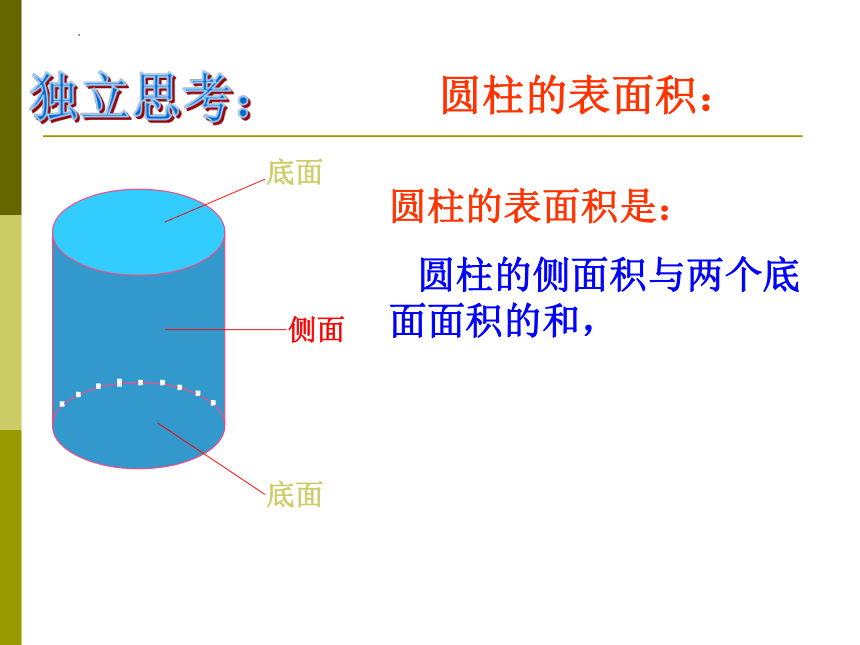
独立思考:
底面
底面
侧面
圆柱的表面积是:
圆柱的侧面积与两个底面面积的和,
圆柱的表面积:
独立思考:
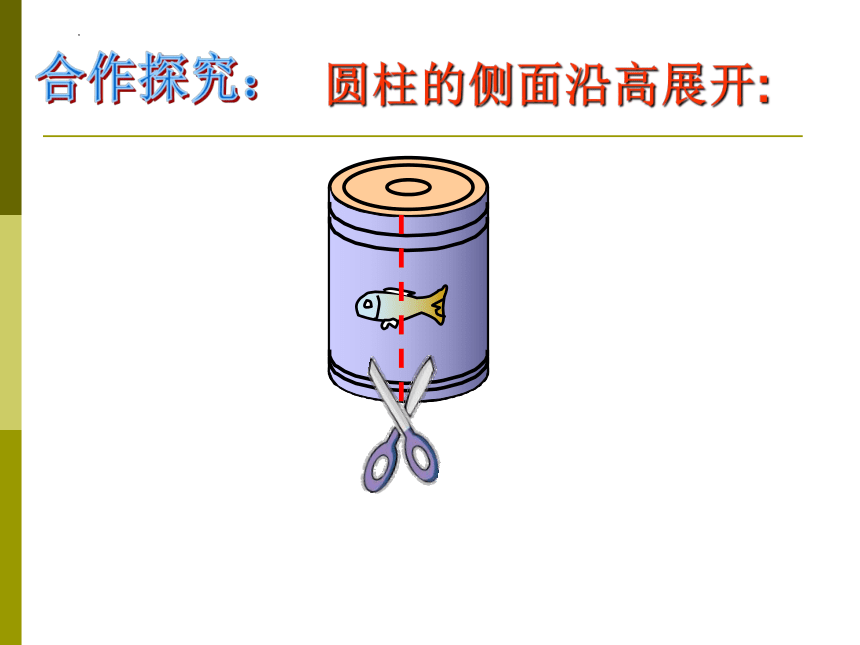
用自己喜欢的方式将手中的圆柱形纸筒剪开,观察展开的图形各部分与圆柱有什么关系?
合作探究:
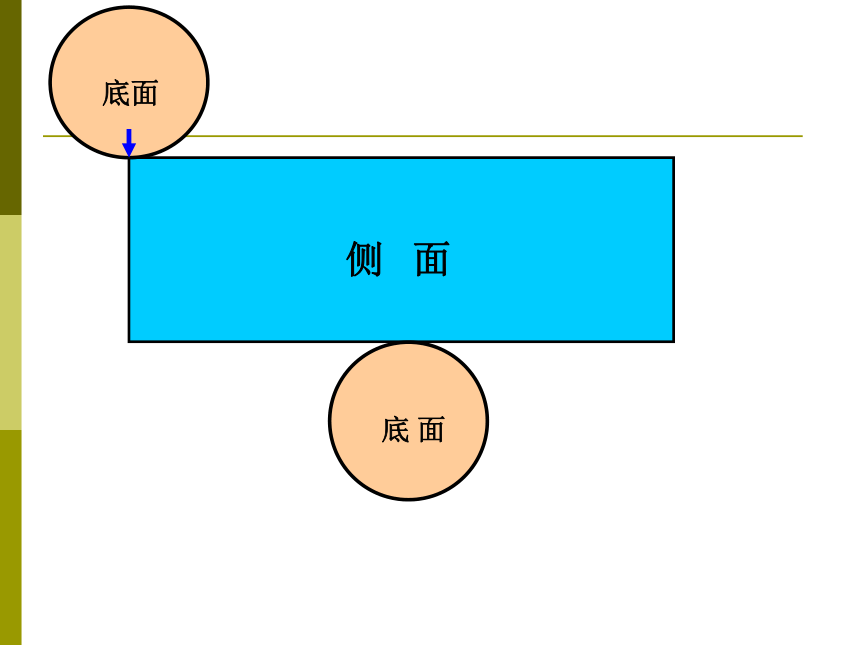
圆柱的侧面沿高展开:
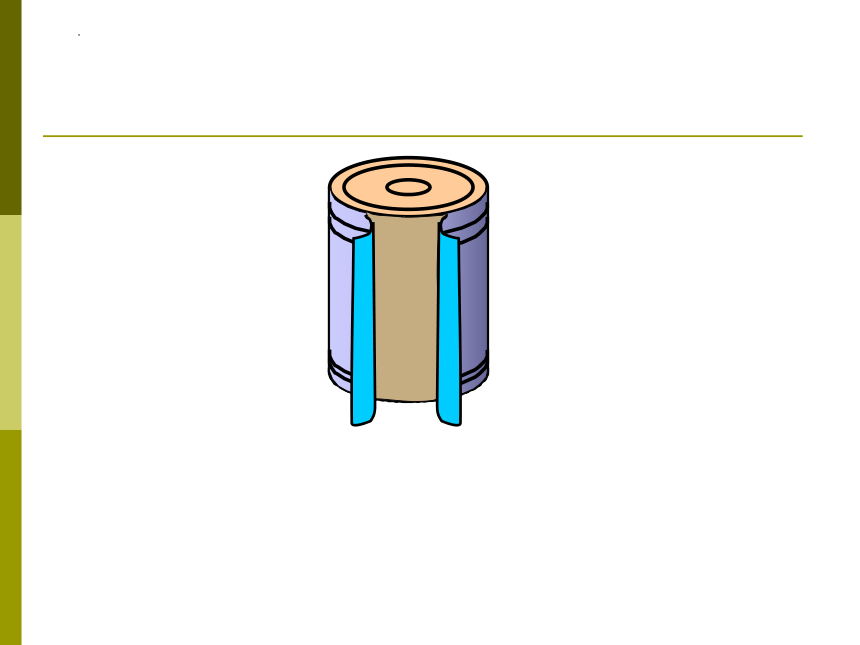
合作探究:
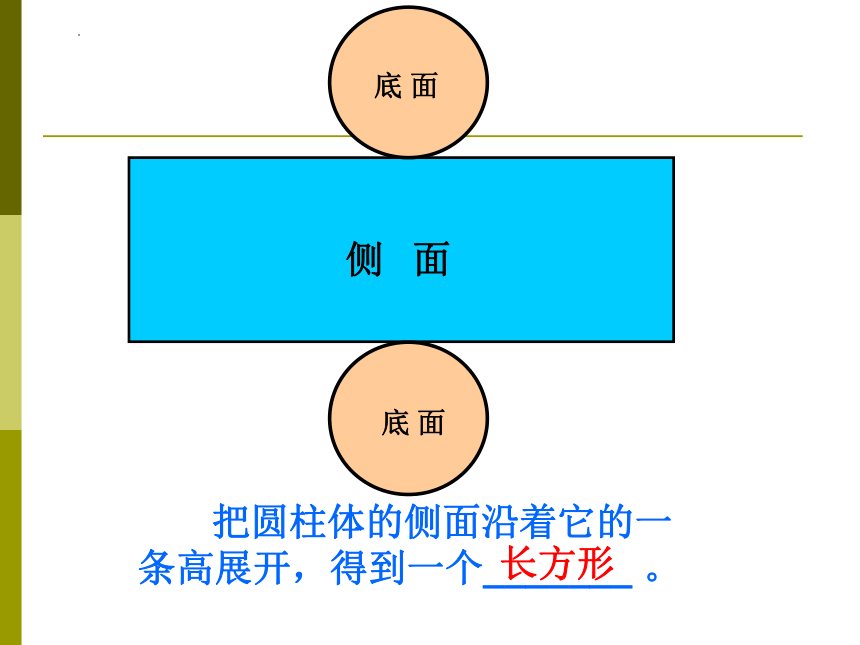
底 面
底 面
侧 面
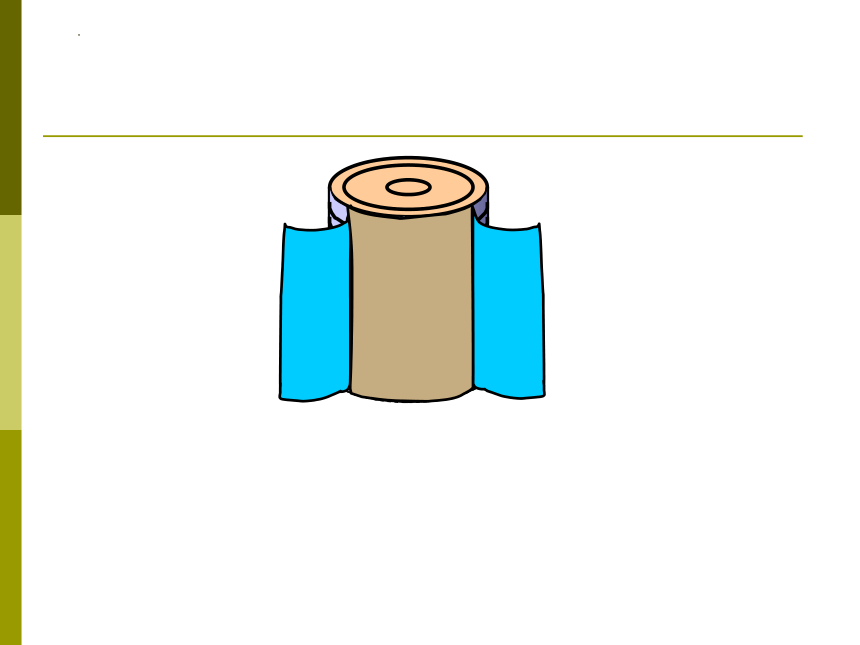
把圆柱体的侧面沿着它的一条高展开,得到一个_______ 。
长方形
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底面的周长
底 面
高
底 面
侧 面
长方形的长=
长方形的宽=
圆柱的底面周长
圆柱的高
圆柱的侧面积=底面周长×高
S侧=Ch
30
10
10
应用:
下列圆柱形物体在计算表面积时有什么不同?
1.用一张长5厘米、宽8厘米的长方形纸围成一个圆柱体,这个圆柱体的侧面积
是 平方厘米。
2.一个底面直径是10厘米、长20厘米的圆柱体,侧面展开成一张长是 厘米
宽是 厘米的长方形。
自我测试:
3.把一个圆柱的侧面沿高剪开,展开后是一个 。如果圆柱的底面周长和高相等,沿高剪开后是一个 ,如果沿斜线剪开,将是 。
自我测试:
4.如右图,压路机的前轮转动1周,压过路的面积是多少平方米?
自我测试:
5.如果一段圆柱形的木头,截成两截,它的表面积会有什么变化呢?
自我测试:
把一根圆柱形木材截成4个相等的圆柱体. 表面积增加了18.84平方分米.
底面的面积是( )
3.14平方分米
4厘米
2厘米
2厘米
8厘米
拓展延伸:
这2种规格的饮料罐可以装同样多的饮料,
如果你作为我的公司总经理,问题:
你准备选择哪种饮料罐生产?为什么?
(小组互相研究一下)
这节课你学到了什么?
注意:
在实际生活中,使用材料要比计划得到得结果要多一些,因此要保留整十平方厘米,都要向前一位进1,这种方法叫进一法。
3.如右图,制作一个底面直径是 20厘米,长是50厘米的圆柱形通风管,至少需要用多少平方厘米的铁皮?
4.如左图,油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克,漆一个油桶大约需要多少防锈油漆?(结果保留两位小数)
答案:20×3.14×50=3140(平方厘米)
答案:[3.14×0.6×1+3.14×(0.6÷2)2×2]×0.2
≈0.49(千克)
思考题
一个圆柱的侧面展开是一个边长为9.42厘米的正方形,这个圆柱的表面积是多少平方厘米?(得数保留两位小数)
9.42×9.42+3.14×(9.42÷3.14÷2)2×2
=88.736+14.13
≈102.87(平方厘米)
答:这个圆柱体的表面积是102.87平方厘米。
需要计算哪几个面的面积?
需要什么条件?
妈妈的生日快要到了,老师想送给妈妈一盒茶叶,需要包装一下,至少要用多少包装纸?(接口处忽略不计)
底面
底面
底面的周长
底面
底面
底面的周长
高
高
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
求下面圆柱的表面积。
4cm
6cm
10cm
3cm
表面积:25.12+75.36
=100.48(c㎡ )
两底面:2×3.14×( )
=25.12(c㎡)
2
4
2
两底面:2×3.14×3
=56.52(c㎡ )
2
侧面:2×3.14×3×10
=188.4(c㎡ )
表面积:56.52+188.4
=244.92(c㎡ )
侧面:2×3.14× ×6
=75.36(c㎡ )
4
2
8cm
C:31.4cm
两底面:2×3.14×5
=2×3.14×25
=157(c㎡ )
2
31.4
2×3.14
r: =5(cm)
求下面圆柱的表面积。
侧面:31.4×8
=251.2(c㎡ )
表面积:157+251.2
=408.2(c㎡ )
应用:
(1)
(2)
(3)
再见
圆柱的表面积
学前准备
独立思考
合作探究
学习体会
自我测试
拓展延伸
请同学们拿出圆柱来看一看,想一想圆柱的表面积包括哪几部分,然后告诉大家。
独立思考:
底面
底面
侧面
圆柱的表面积是:
圆柱的侧面积与两个底面面积的和,
圆柱的表面积:
独立思考:
用自己喜欢的方式将手中的圆柱形纸筒剪开,观察展开的图形各部分与圆柱有什么关系?
合作探究:
圆柱的侧面沿高展开:
合作探究:
底 面
底 面
侧 面
把圆柱体的侧面沿着它的一条高展开,得到一个_______ 。
长方形
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底 面
底 面
侧 面
底面的周长
底 面
高
底 面
侧 面
长方形的长=
长方形的宽=
圆柱的底面周长
圆柱的高
圆柱的侧面积=底面周长×高
S侧=Ch
30
10
10
应用:
下列圆柱形物体在计算表面积时有什么不同?
1.用一张长5厘米、宽8厘米的长方形纸围成一个圆柱体,这个圆柱体的侧面积
是 平方厘米。
2.一个底面直径是10厘米、长20厘米的圆柱体,侧面展开成一张长是 厘米
宽是 厘米的长方形。
自我测试:
3.把一个圆柱的侧面沿高剪开,展开后是一个 。如果圆柱的底面周长和高相等,沿高剪开后是一个 ,如果沿斜线剪开,将是 。
自我测试:
4.如右图,压路机的前轮转动1周,压过路的面积是多少平方米?
自我测试:
5.如果一段圆柱形的木头,截成两截,它的表面积会有什么变化呢?
自我测试:
把一根圆柱形木材截成4个相等的圆柱体. 表面积增加了18.84平方分米.
底面的面积是( )
3.14平方分米
4厘米
2厘米
2厘米
8厘米
拓展延伸:
这2种规格的饮料罐可以装同样多的饮料,
如果你作为我的公司总经理,问题:
你准备选择哪种饮料罐生产?为什么?
(小组互相研究一下)
这节课你学到了什么?
注意:
在实际生活中,使用材料要比计划得到得结果要多一些,因此要保留整十平方厘米,都要向前一位进1,这种方法叫进一法。
3.如右图,制作一个底面直径是 20厘米,长是50厘米的圆柱形通风管,至少需要用多少平方厘米的铁皮?
4.如左图,油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克,漆一个油桶大约需要多少防锈油漆?(结果保留两位小数)
答案:20×3.14×50=3140(平方厘米)
答案:[3.14×0.6×1+3.14×(0.6÷2)2×2]×0.2
≈0.49(千克)
思考题
一个圆柱的侧面展开是一个边长为9.42厘米的正方形,这个圆柱的表面积是多少平方厘米?(得数保留两位小数)
9.42×9.42+3.14×(9.42÷3.14÷2)2×2
=88.736+14.13
≈102.87(平方厘米)
答:这个圆柱体的表面积是102.87平方厘米。
需要计算哪几个面的面积?
需要什么条件?
妈妈的生日快要到了,老师想送给妈妈一盒茶叶,需要包装一下,至少要用多少包装纸?(接口处忽略不计)
底面
底面
底面的周长
底面
底面
底面的周长
高
高
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
求下面圆柱的表面积。
4cm
6cm
10cm
3cm
表面积:25.12+75.36
=100.48(c㎡ )
两底面:2×3.14×( )
=25.12(c㎡)
2
4
2
两底面:2×3.14×3
=56.52(c㎡ )
2
侧面:2×3.14×3×10
=188.4(c㎡ )
表面积:56.52+188.4
=244.92(c㎡ )
侧面:2×3.14× ×6
=75.36(c㎡ )
4
2
8cm
C:31.4cm
两底面:2×3.14×5
=2×3.14×25
=157(c㎡ )
2
31.4
2×3.14
r: =5(cm)
求下面圆柱的表面积。
侧面:31.4×8
=251.2(c㎡ )
表面积:157+251.2
=408.2(c㎡ )
应用:
(1)
(2)
(3)
再见
