18.1.2.2 三角形的中位线 同步训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.1.2.2 三角形的中位线 同步训练(含答案)初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 318.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 10:47:10 | ||
图片预览

文档简介
第十八章 平行四边形
18.1.2 平行四边形的判定
第2课时 三角形的中位线
一、选择题
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3米,则AB=( )
A.4米 B.6米
C.8米 D.10米
2.如图,在△ABC中,D,E分别是AB,AC的中点,∠C=45°,∠A=50°,则∠ADE的度数为( )
A.95° B.85°
C.75° D.50°
3.如图,△ABC是等边三角形,D,E分别是AB,AC的中点,连接DE,若AB=10,则△ADE的周长为( )
A.15 B.20
C.25 D.30
4.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个
C.3个 D.4个
5.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( )
A.15° B.25°
C.30° D.35°
7.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=9,DM=2,则AB等于( )
A.4 B.5 C.6 D.8
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
二、填空题
9.如图,在 ABCD中,点M为边AD上一点,AM=2MD,E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
10.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
11.如图,在四边形ABCD中,E,F,G,H分别是BD,BC,AC,AD的中点,若AB=CD=2,则四边形EFGH的周长是 .
12.如图,△ABC的周长是1,连接△ABC三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,依此类推,第2024个三角形的周长为_______.
三、解答题
13.如图所示,在△ABC 中,D,E分别为AB,AC的中点,点H在线段CE上,连接BH,G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
14.在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.求证:EF=(AB-AC).
15.如图,C为线段BD上一点,分别以BC,CD为腰作等腰三角形ABC和等腰三角形ECD,顶角∠ACB与顶角∠ECD相等,P,F分别为BD,ED的中点,连接AD,PF.求证:PF=AD.
16.如图,四边形ABCD为平行四边形,E为AC上一点,延长BE至点F,使EF=BE,BF交CD于点G,连接DF.
(1)求证:DF∥AC;
(2)若BF⊥CD,∠AEB=60°,求证:AE-CE=2GF.
1
参考答案
一、选择题
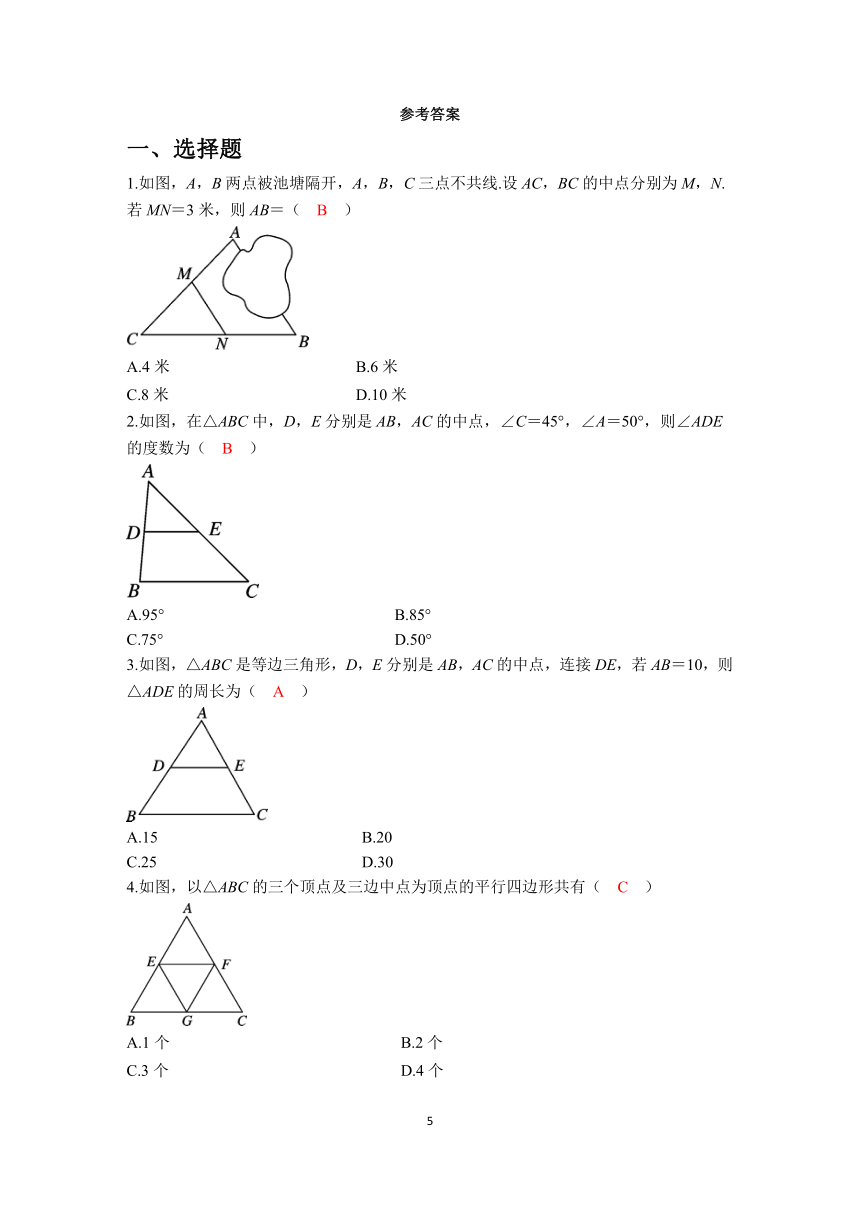
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3米,则AB=( B )
A.4米 B.6米
C.8米 D.10米
2.如图,在△ABC中,D,E分别是AB,AC的中点,∠C=45°,∠A=50°,则∠ADE的度数为( B )
A.95° B.85°
C.75° D.50°
3.如图,△ABC是等边三角形,D,E分别是AB,AC的中点,连接DE,若AB=10,则△ADE的周长为( A )
A.15 B.20
C.25 D.30
4.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( C )
A.1个 B.2个
C.3个 D.4个
5.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( A )
A.1 B.2 C.3 D.4
6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( D )
A.15° B.25°
C.30° D.35°
7.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=9,DM=2,则AB等于( B )
A.4 B.5 C.6 D.8
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( C )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
二、填空题
9.如图,在 ABCD中,点M为边AD上一点,AM=2MD,E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
【答案】8
10.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
【答案】135°
11.如图,在四边形ABCD中,E,F,G,H分别是BD,BC,AC,AD的中点,若AB=CD=2,则四边形EFGH的周长是 .
【答案】4
12.如图,△ABC的周长是1,连接△ABC三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,依此类推,第2024个三角形的周长为_______.
【答案】
三、解答题
13.如图所示,在△ABC 中,D,E分别为AB,AC的中点,点H在线段CE上,连接BH,G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
解:(1)证明:∵D,E分别为AB,AC的
中点,G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,
GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
解:(2)∵四边形DEFG为平行四边形,
∴DG=EF=2.
∵DG⊥BH,∴∠DGB=90°.
∴BG===.
即线段BG的长度为.
14.在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.求证:EF=(AB-AC).
证明:如图,延长AC交BE的延长线于点P,∵AE⊥BP,∴∠AEP=∠AEB=90°,∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,∵AE平分∠BAP,∴∠BAE=∠PAE,∴∠ABE=∠APE,∴AB=AP,又∵AE⊥BP,∴BE=PE.∵F是BC的中点,∴BF=FC,∴EF=PC=(AP-AC)=(AB-AC)
15.如图,C为线段BD上一点,分别以BC,CD为腰作等腰三角形ABC和等腰三角形ECD,顶角∠ACB与顶角∠ECD相等,P,F分别为BD,ED的中点,连接AD,PF.求证:PF=AD.
证明:连接BE.
∵BP=DP,EF=DF,
∴PF为△BDE的中位线.
∴PF=BE.
∵∠BCE=∠ACB+∠ACE,
∠ACD=∠ECD+∠ACE,∠ACB=∠ECD,∴∠BCE=∠ACD.
又∵BC=AC,EC=DC,
∴△BCE≌△ACD.
∴BE=AD.∴PF=AD.
16.如图,四边形ABCD为平行四边形,E为AC上一点,延长BE至点F,使EF=BE,BF交CD于点G,连接DF.
(1)求证:DF∥AC;
(2)若BF⊥CD,∠AEB=60°,求证:AE-CE=2GF.
证明:(1)连接BD交AC于点O.
∵四边形ABCD为平行四边形,
∴OB=OD.
∵BE=EF,∴OE为△BDF的中位线.
∴DF∥AC.
证明:(2)∵四边形ABCD为平行四边形,
∴AO=OC.
∵OE为△BDF的中位线,
∴OE DF.∴∠F=∠AEB=60°.
∵∠DGF=90°,∴∠FDG=30°.∴DF=2GF.
∴AE-CE=(AO+OE)-(OC-OE)=2OE
=DF=2GF.
18.1.2 平行四边形的判定
第2课时 三角形的中位线
一、选择题
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3米,则AB=( )
A.4米 B.6米
C.8米 D.10米
2.如图,在△ABC中,D,E分别是AB,AC的中点,∠C=45°,∠A=50°,则∠ADE的度数为( )
A.95° B.85°
C.75° D.50°
3.如图,△ABC是等边三角形,D,E分别是AB,AC的中点,连接DE,若AB=10,则△ADE的周长为( )
A.15 B.20
C.25 D.30
4.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个
C.3个 D.4个
5.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( )
A.15° B.25°
C.30° D.35°
7.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=9,DM=2,则AB等于( )
A.4 B.5 C.6 D.8
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
二、填空题
9.如图,在 ABCD中,点M为边AD上一点,AM=2MD,E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
10.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
11.如图,在四边形ABCD中,E,F,G,H分别是BD,BC,AC,AD的中点,若AB=CD=2,则四边形EFGH的周长是 .
12.如图,△ABC的周长是1,连接△ABC三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,依此类推,第2024个三角形的周长为_______.
三、解答题
13.如图所示,在△ABC 中,D,E分别为AB,AC的中点,点H在线段CE上,连接BH,G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
14.在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.求证:EF=(AB-AC).
15.如图,C为线段BD上一点,分别以BC,CD为腰作等腰三角形ABC和等腰三角形ECD,顶角∠ACB与顶角∠ECD相等,P,F分别为BD,ED的中点,连接AD,PF.求证:PF=AD.
16.如图,四边形ABCD为平行四边形,E为AC上一点,延长BE至点F,使EF=BE,BF交CD于点G,连接DF.
(1)求证:DF∥AC;
(2)若BF⊥CD,∠AEB=60°,求证:AE-CE=2GF.
1
参考答案
一、选择题
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3米,则AB=( B )
A.4米 B.6米
C.8米 D.10米
2.如图,在△ABC中,D,E分别是AB,AC的中点,∠C=45°,∠A=50°,则∠ADE的度数为( B )
A.95° B.85°
C.75° D.50°
3.如图,△ABC是等边三角形,D,E分别是AB,AC的中点,连接DE,若AB=10,则△ADE的周长为( A )
A.15 B.20
C.25 D.30
4.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( C )
A.1个 B.2个
C.3个 D.4个
5.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( A )
A.1 B.2 C.3 D.4
6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( D )
A.15° B.25°
C.30° D.35°
7.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=9,DM=2,则AB等于( B )
A.4 B.5 C.6 D.8
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( C )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
二、填空题
9.如图,在 ABCD中,点M为边AD上一点,AM=2MD,E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
【答案】8
10.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
【答案】135°
11.如图,在四边形ABCD中,E,F,G,H分别是BD,BC,AC,AD的中点,若AB=CD=2,则四边形EFGH的周长是 .
【答案】4
12.如图,△ABC的周长是1,连接△ABC三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,依此类推,第2024个三角形的周长为_______.
【答案】
三、解答题
13.如图所示,在△ABC 中,D,E分别为AB,AC的中点,点H在线段CE上,连接BH,G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
解:(1)证明:∵D,E分别为AB,AC的
中点,G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,
GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
解:(2)∵四边形DEFG为平行四边形,
∴DG=EF=2.
∵DG⊥BH,∴∠DGB=90°.
∴BG===.
即线段BG的长度为.
14.在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.求证:EF=(AB-AC).
证明:如图,延长AC交BE的延长线于点P,∵AE⊥BP,∴∠AEP=∠AEB=90°,∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,∵AE平分∠BAP,∴∠BAE=∠PAE,∴∠ABE=∠APE,∴AB=AP,又∵AE⊥BP,∴BE=PE.∵F是BC的中点,∴BF=FC,∴EF=PC=(AP-AC)=(AB-AC)
15.如图,C为线段BD上一点,分别以BC,CD为腰作等腰三角形ABC和等腰三角形ECD,顶角∠ACB与顶角∠ECD相等,P,F分别为BD,ED的中点,连接AD,PF.求证:PF=AD.
证明:连接BE.
∵BP=DP,EF=DF,
∴PF为△BDE的中位线.
∴PF=BE.
∵∠BCE=∠ACB+∠ACE,
∠ACD=∠ECD+∠ACE,∠ACB=∠ECD,∴∠BCE=∠ACD.
又∵BC=AC,EC=DC,
∴△BCE≌△ACD.
∴BE=AD.∴PF=AD.
16.如图,四边形ABCD为平行四边形,E为AC上一点,延长BE至点F,使EF=BE,BF交CD于点G,连接DF.
(1)求证:DF∥AC;
(2)若BF⊥CD,∠AEB=60°,求证:AE-CE=2GF.
证明:(1)连接BD交AC于点O.
∵四边形ABCD为平行四边形,
∴OB=OD.
∵BE=EF,∴OE为△BDF的中位线.
∴DF∥AC.
证明:(2)∵四边形ABCD为平行四边形,
∴AO=OC.
∵OE为△BDF的中位线,
∴OE DF.∴∠F=∠AEB=60°.
∵∠DGF=90°,∴∠FDG=30°.∴DF=2GF.
∴AE-CE=(AO+OE)-(OC-OE)=2OE
=DF=2GF.
