第八章 8.6.3 平面与平面垂直(第1课时)(共27张PPT)
文档属性
| 名称 | 第八章 8.6.3 平面与平面垂直(第1课时)(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 10:30:47 | ||
图片预览




文档简介
(共27张PPT)
第七章
8.6.3 平面与平面垂直(第1课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.理解二面角及其相关概念; 1.几何直观素养.
2.掌握平面与平面垂直的定义及判定定理. 2.空间想象素养和数学抽象素养.
3.运用平面与平面垂直的判定定理证明平面与平面垂直问题. 3.几何直观素养和逻辑推理素养.
温故知新
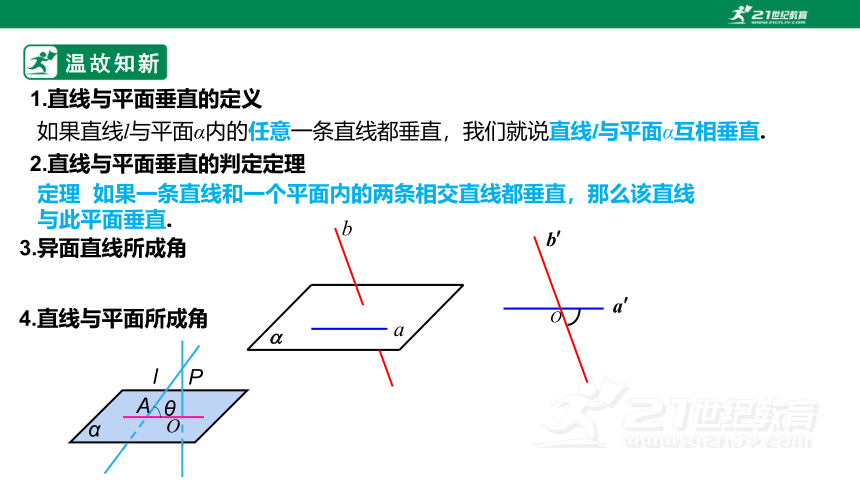
1.直线与平面垂直的定义
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.
2.直线与平面垂直的判定定理
定理 如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
3.异面直线所成角
a
b
O
4.直线与平面所成角
α
l
P
A
θ
新知引入
在定义直线与平面垂直时,我们利用了直线与直线垂直.所以直线与直线垂直是研究直线、平面垂直的基础.
在平面几何中,我们 先定义了角的概念,利用角刻画两条相交直线的位置关系,进而研究直线与直线互相垂直这种特殊情况类似地,我们需要先引进二面角的概念,用以刻画两个相交平面的位置关系,进而研究两个平面互相垂直.
水坝在修建的时候,为了坚固耐用,水坝的坡面与水平面要成一个适当的角度.
虚掩的门是指门和墙面什么关系?
新知探究
l
A
B
β
α
·P
·Q
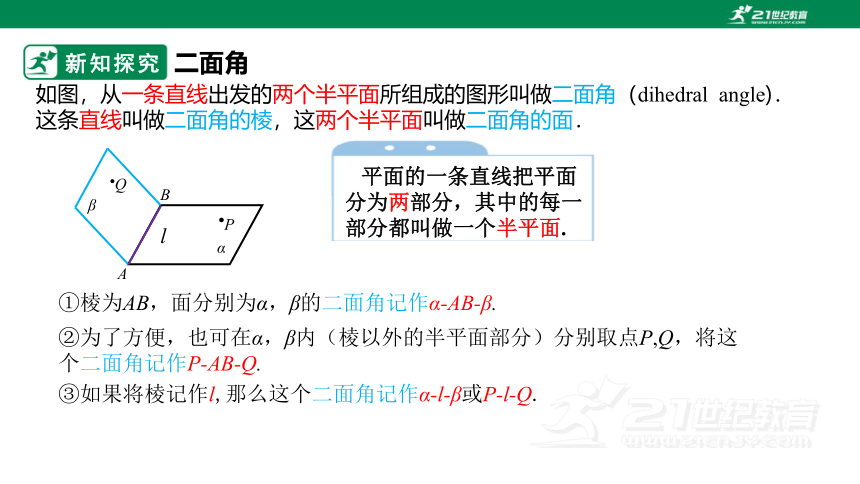
如图,从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).
这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
平面的一条直线把平面分为两部分,其中的每一部分都叫做一个半平面.
①棱为AB,面分别为α,β的二面角记作α-AB-β.
②为了方便,也可在α,β内(棱以外的半平面部分)分别取点P,Q,将这个二面角记作P-AB-Q.
③如果将棱记作l,那么这个二面角记作α-l-β或P-l-Q.
二面角
新知探究
在日常生活中,有很多平面与平面相交的例子.比如笔记本电脑打开过程中,屏幕和键盘所在的平面相交并形成了一定的角度;
书的两个页面;折截手机的两个面等.
二面角
新知探究
二面角的平面角
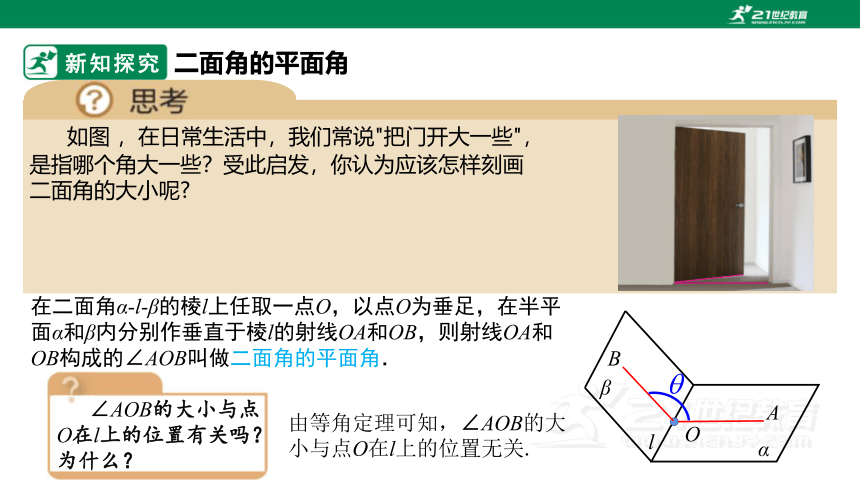
如图 ,在日常生活中,我们常说"把门开大一些",
是指哪个角大一些?受此启发,你认为应该怎样刻画
二面角的大小呢
在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
β
α
l
O
A
B
∠AOB的大小与点O在l上的位置有关吗?
为什么?
由等角定理可知,∠AOB的大小与点O在l上的位置无关.
新知探究
二面角的平面角
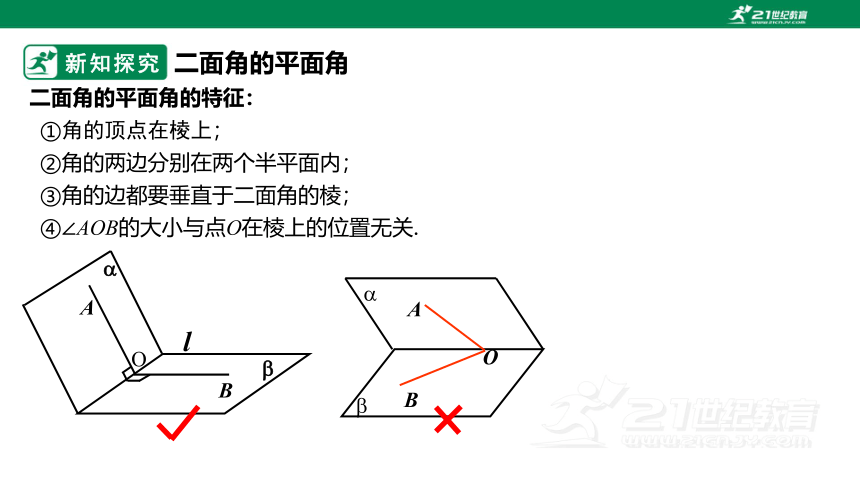
二面角的平面角的特征:
①角的顶点在棱上;
②角的两边分别在两个半平面内;
③角的边都要垂直于二面角的棱;
④∠AOB的大小与点O在棱上的位置无关.
l
O
A
B
A
O
B
新知探究
二面角的平面角
β
α
l
O
A
B
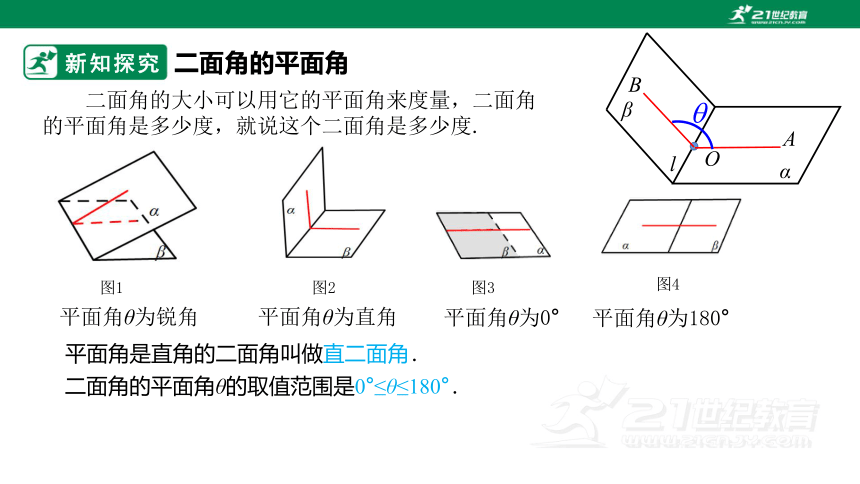
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.
图1
平面角θ为锐角
图2
平面角θ为直角
图3
平面角θ为0°
图4
平面角θ为180°
平面角是直角的二面角叫做直二面角.
二面角的平面角θ的取值范围是0°≤θ≤180°.
新知探究
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室的墙面所在平面与地面所在平面相交,它们所成的二面角是直二面角,我们常说墙面直立于地面上.
一般地, 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与β垂直,记作α⊥β.
如图 ,画两个互相垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直.
在明确了两个平面相互垂直的定义的基础上,我们先研究平面与平面垂直的判定.
两个平面互相垂直的定义
知新探究
如图,建筑工人在砌墙时,常用铅锤来检测所砌的墙面与
地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认
为墙面垂直于地面,否则他就认为墙面不垂直于地面.这种方
法说明了什么道理?
这种方法告诉我们,如果墙面经过地面的垂线,那么墙面与地面垂直.
类似的结论也可以在长方体中发现.如图,在长方体ABCD-A′B′C′D′中,平面ABB′A′经过平面ABCD的一条垂线AA′,此时,平面ABB′A′垂直于平面ABCD.
两个平面互相垂直的判定定理
知新探究
一般地,我们有下面判定两个平面互相垂直的定理:
定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
图形语言表示
符号语言表示
a α,a⊥β α⊥β.
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
线线垂直
面面垂直
两个平面互相垂直的判定定理
知新探究
已知:a⊥β,a α,a∩α=O.
求证:α⊥β.
证明:
设α∩β=l,则O∈l.
∴a⊥b,
则直线a与直线b所成角是二面角α-l-β的平面角.
∴α⊥β.
在平面内过点O作直线b⊥l..
∴a⊥l.
O
l
∵a⊥β,l β
b
又∵a⊥β,b β
即二面角α-l-β的平面角是直二面角.
两个平面互相垂直的判定定理
知新探究
【例1】如图,在正方体ABCD-A'B'C'D'中,求证:平面A'BD⊥平面ACC'A'.
证明:
∴AA'⊥BD,
∵ABCD-A'B'C'D'是正方体
分析:要证平面A'BD⊥平面ACC'A',根据两个平面垂直的判定定理,只要证明平面A'BD经过平面ACC'A'的一条垂线即可.这需要利用AC、BD是正方形ABCD的对角线.
∴AA'⊥平面ABCD.
又BD⊥AC,AA'∩AC=AC,
∴平面A'BD⊥平面ACC'A'.
∴BD⊥平面ACC'A'.
注意:①直棱柱侧棱垂直于底面的任一条直线;
②正方形的对角线互相垂直.
知新探究
【例2】如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC.
分析:要证两个平面垂直,根据两个平面垂直的判定定理,
只需证明其中一个平面中的一条直线垂直于另一个平面,而
由直线与平面垂直的判定定理,还需证明这条直线与另一个平面内的两条相交直线垂直.
在本题中,由题意可知,BC⊥AC,BC⊥PA,AC∩PA=A,从而BC⊥平面PAC,进而平面PAC⊥平面PBC.
知新探究
【例2】如图所示,AB是 O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC.
证明:
又PA∩AC=A,PA 平面PAC,AC 平面PAC,
∴PA⊥BC.
∵PA⊥平面ABC,BC 平面ABC,
∴∠BCA=90°,即BC⊥AC.
∵C是圆周上不同于A,B的任意一点,AB是 O的直径,
∴BC⊥平面PAC,
∴平面PAC⊥平面PBC.
知新探究
【例3】如图,AC⊥平面BCD,BD⊥CD,AD=2AC,二面角A BD C的大小为 .
解:
∵AC⊥平面BCD,BD 平面BCD,
∴AC⊥BD.
又BD⊥CD,AC∩CD=C,
∴BD⊥平面ACD,
∴∠ADC即为二面角A BD C的平面角.
∵AD⊥BD,
在Rt△ACD中,AD=2AC,
∴∠ADC=30°,即二面角A BD C为30°.
30°
初试身手
1.如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明:
方法1:(利用定义)∵∠BSA=∠CSA=60°,SA=SB=SC,
∴△ASB和△ASC都是等边三角形,
令其值为a,则△ABC和△SBC为共底边BC的等腰三角形.
∴∠ADS=90°,即二面角A-BC-S为直二面角,
则AD⊥BC,SD⊥BC,
SD=,BD==.
则有SA=SB=SC=AB=AC,
∴∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,SB=SC=a,
如图所示,取BC的中点D,连接AD,SD,
在Rt△ABD中,AD=,在△ADS中,∵SD2+AD2=SA2,
故平面ABC⊥平面SBC.
初试身手
1.如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明:
方法2:(利用判定定理)
∵∠BSA=∠CSA=60°,SA=SB=SC,
∴点A在平面SBC上的射影为△SBC的外心.
∴SA=AB=AC,
∴点A在△SBC上的射影D为斜边BC的中点,
∴AD⊥平面SBC.
∵△SBC为直角三角形,
又∵AD 平面ABC,
∴平面ABC⊥平面SBC.
初试身手
证明:
⑵∵E,F分别为AC,AB的中点,
⑴∵E,P分别为AC,A'C的中点,
∵BC⊥AC,
∴EP∥平面AA'B,即EP∥平面A'FB.
∴EF∥BC.
2.如图,E,F分别为Rt△ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,连接A'B,A'C,P为A'C的中点.
⑴求证:EP∥平面A'FB;
⑵求证:平面A'EC⊥平面A'BC.
∴EP∥AA',
又AA' 平面AA'B,EP 平面AA'B,
∴EF⊥AC.
∴EF⊥A'E,
∴BC⊥A'E,
又A'E∩AC=E,
∴BC⊥平面A'EC,
∵BC 平面A'BC,
∴平面A'EC⊥平面A'BC.
初试身手
3.如图,在正方体ABCD -A1B1C1D1中,二面角D1-AB-C的大小是 .
解:
∵AB⊥平面BB1C1C,且BC1 平面BB1C1C,
又∵AB⊥BC,
而∠C1BC=45°,
在正方体ABCD -A1B1C1D1中,
∴二面角D1-AB-C的大小为45°.
∴AB⊥BC1,
∴∠C1BC为二面角D1-AB-C的平面角,
45°
课堂小结
1.二面角及其相关概念
2.两个平面互相垂直的定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
β
α
l
O
A
B
平面角是直角的二面角叫做直二面角.
二面角的平面角θ的取值范围是0°≤θ≤180°.
一般地, 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与β垂直,记作α⊥β.
课堂小结
3.两个平面互相垂直的判定定理
定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
图形语言表示
符号语言表示
a α,a⊥β α⊥β.
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
线线垂直
面面垂直
作业布置
作业: P159 练习 第3, 4题
P163 习题8.6 第6, 7,8题
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第七章
8.6.3 平面与平面垂直(第1课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.理解二面角及其相关概念; 1.几何直观素养.
2.掌握平面与平面垂直的定义及判定定理. 2.空间想象素养和数学抽象素养.
3.运用平面与平面垂直的判定定理证明平面与平面垂直问题. 3.几何直观素养和逻辑推理素养.
温故知新
1.直线与平面垂直的定义
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.
2.直线与平面垂直的判定定理
定理 如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
3.异面直线所成角
a
b
O
4.直线与平面所成角
α
l
P
A
θ
新知引入
在定义直线与平面垂直时,我们利用了直线与直线垂直.所以直线与直线垂直是研究直线、平面垂直的基础.
在平面几何中,我们 先定义了角的概念,利用角刻画两条相交直线的位置关系,进而研究直线与直线互相垂直这种特殊情况类似地,我们需要先引进二面角的概念,用以刻画两个相交平面的位置关系,进而研究两个平面互相垂直.
水坝在修建的时候,为了坚固耐用,水坝的坡面与水平面要成一个适当的角度.
虚掩的门是指门和墙面什么关系?
新知探究
l
A
B
β
α
·P
·Q
如图,从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).
这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
平面的一条直线把平面分为两部分,其中的每一部分都叫做一个半平面.
①棱为AB,面分别为α,β的二面角记作α-AB-β.
②为了方便,也可在α,β内(棱以外的半平面部分)分别取点P,Q,将这个二面角记作P-AB-Q.
③如果将棱记作l,那么这个二面角记作α-l-β或P-l-Q.
二面角
新知探究
在日常生活中,有很多平面与平面相交的例子.比如笔记本电脑打开过程中,屏幕和键盘所在的平面相交并形成了一定的角度;
书的两个页面;折截手机的两个面等.
二面角
新知探究
二面角的平面角
如图 ,在日常生活中,我们常说"把门开大一些",
是指哪个角大一些?受此启发,你认为应该怎样刻画
二面角的大小呢
在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
β
α
l
O
A
B
∠AOB的大小与点O在l上的位置有关吗?
为什么?
由等角定理可知,∠AOB的大小与点O在l上的位置无关.
新知探究
二面角的平面角
二面角的平面角的特征:
①角的顶点在棱上;
②角的两边分别在两个半平面内;
③角的边都要垂直于二面角的棱;
④∠AOB的大小与点O在棱上的位置无关.
l
O
A
B
A
O
B
新知探究
二面角的平面角
β
α
l
O
A
B
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.
图1
平面角θ为锐角
图2
平面角θ为直角
图3
平面角θ为0°
图4
平面角θ为180°
平面角是直角的二面角叫做直二面角.
二面角的平面角θ的取值范围是0°≤θ≤180°.
新知探究
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室的墙面所在平面与地面所在平面相交,它们所成的二面角是直二面角,我们常说墙面直立于地面上.
一般地, 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与β垂直,记作α⊥β.
如图 ,画两个互相垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直.
在明确了两个平面相互垂直的定义的基础上,我们先研究平面与平面垂直的判定.
两个平面互相垂直的定义
知新探究
如图,建筑工人在砌墙时,常用铅锤来检测所砌的墙面与
地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认
为墙面垂直于地面,否则他就认为墙面不垂直于地面.这种方
法说明了什么道理?
这种方法告诉我们,如果墙面经过地面的垂线,那么墙面与地面垂直.
类似的结论也可以在长方体中发现.如图,在长方体ABCD-A′B′C′D′中,平面ABB′A′经过平面ABCD的一条垂线AA′,此时,平面ABB′A′垂直于平面ABCD.
两个平面互相垂直的判定定理
知新探究
一般地,我们有下面判定两个平面互相垂直的定理:
定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
图形语言表示
符号语言表示
a α,a⊥β α⊥β.
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
线线垂直
面面垂直
两个平面互相垂直的判定定理
知新探究
已知:a⊥β,a α,a∩α=O.
求证:α⊥β.
证明:
设α∩β=l,则O∈l.
∴a⊥b,
则直线a与直线b所成角是二面角α-l-β的平面角.
∴α⊥β.
在平面内过点O作直线b⊥l..
∴a⊥l.
O
l
∵a⊥β,l β
b
又∵a⊥β,b β
即二面角α-l-β的平面角是直二面角.
两个平面互相垂直的判定定理
知新探究
【例1】如图,在正方体ABCD-A'B'C'D'中,求证:平面A'BD⊥平面ACC'A'.
证明:
∴AA'⊥BD,
∵ABCD-A'B'C'D'是正方体
分析:要证平面A'BD⊥平面ACC'A',根据两个平面垂直的判定定理,只要证明平面A'BD经过平面ACC'A'的一条垂线即可.这需要利用AC、BD是正方形ABCD的对角线.
∴AA'⊥平面ABCD.
又BD⊥AC,AA'∩AC=AC,
∴平面A'BD⊥平面ACC'A'.
∴BD⊥平面ACC'A'.
注意:①直棱柱侧棱垂直于底面的任一条直线;
②正方形的对角线互相垂直.
知新探究
【例2】如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC.
分析:要证两个平面垂直,根据两个平面垂直的判定定理,
只需证明其中一个平面中的一条直线垂直于另一个平面,而
由直线与平面垂直的判定定理,还需证明这条直线与另一个平面内的两条相交直线垂直.
在本题中,由题意可知,BC⊥AC,BC⊥PA,AC∩PA=A,从而BC⊥平面PAC,进而平面PAC⊥平面PBC.
知新探究
【例2】如图所示,AB是 O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC.
证明:
又PA∩AC=A,PA 平面PAC,AC 平面PAC,
∴PA⊥BC.
∵PA⊥平面ABC,BC 平面ABC,
∴∠BCA=90°,即BC⊥AC.
∵C是圆周上不同于A,B的任意一点,AB是 O的直径,
∴BC⊥平面PAC,
∴平面PAC⊥平面PBC.
知新探究
【例3】如图,AC⊥平面BCD,BD⊥CD,AD=2AC,二面角A BD C的大小为 .
解:
∵AC⊥平面BCD,BD 平面BCD,
∴AC⊥BD.
又BD⊥CD,AC∩CD=C,
∴BD⊥平面ACD,
∴∠ADC即为二面角A BD C的平面角.
∵AD⊥BD,
在Rt△ACD中,AD=2AC,
∴∠ADC=30°,即二面角A BD C为30°.
30°
初试身手
1.如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明:
方法1:(利用定义)∵∠BSA=∠CSA=60°,SA=SB=SC,
∴△ASB和△ASC都是等边三角形,
令其值为a,则△ABC和△SBC为共底边BC的等腰三角形.
∴∠ADS=90°,即二面角A-BC-S为直二面角,
则AD⊥BC,SD⊥BC,
SD=,BD==.
则有SA=SB=SC=AB=AC,
∴∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,SB=SC=a,
如图所示,取BC的中点D,连接AD,SD,
在Rt△ABD中,AD=,在△ADS中,∵SD2+AD2=SA2,
故平面ABC⊥平面SBC.
初试身手
1.如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明:
方法2:(利用判定定理)
∵∠BSA=∠CSA=60°,SA=SB=SC,
∴点A在平面SBC上的射影为△SBC的外心.
∴SA=AB=AC,
∴点A在△SBC上的射影D为斜边BC的中点,
∴AD⊥平面SBC.
∵△SBC为直角三角形,
又∵AD 平面ABC,
∴平面ABC⊥平面SBC.
初试身手
证明:
⑵∵E,F分别为AC,AB的中点,
⑴∵E,P分别为AC,A'C的中点,
∵BC⊥AC,
∴EP∥平面AA'B,即EP∥平面A'FB.
∴EF∥BC.
2.如图,E,F分别为Rt△ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,连接A'B,A'C,P为A'C的中点.
⑴求证:EP∥平面A'FB;
⑵求证:平面A'EC⊥平面A'BC.
∴EP∥AA',
又AA' 平面AA'B,EP 平面AA'B,
∴EF⊥AC.
∴EF⊥A'E,
∴BC⊥A'E,
又A'E∩AC=E,
∴BC⊥平面A'EC,
∵BC 平面A'BC,
∴平面A'EC⊥平面A'BC.
初试身手
3.如图,在正方体ABCD -A1B1C1D1中,二面角D1-AB-C的大小是 .
解:
∵AB⊥平面BB1C1C,且BC1 平面BB1C1C,
又∵AB⊥BC,
而∠C1BC=45°,
在正方体ABCD -A1B1C1D1中,
∴二面角D1-AB-C的大小为45°.
∴AB⊥BC1,
∴∠C1BC为二面角D1-AB-C的平面角,
45°
课堂小结
1.二面角及其相关概念
2.两个平面互相垂直的定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
β
α
l
O
A
B
平面角是直角的二面角叫做直二面角.
二面角的平面角θ的取值范围是0°≤θ≤180°.
一般地, 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与β垂直,记作α⊥β.
课堂小结
3.两个平面互相垂直的判定定理
定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
图形语言表示
符号语言表示
a α,a⊥β α⊥β.
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
线线垂直
面面垂直
作业布置
作业: P159 练习 第3, 4题
P163 习题8.6 第6, 7,8题
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
