5.面积 单元测评卷 人教版数学 三年级下册(含解析)
文档属性
| 名称 | 5.面积 单元测评卷 人教版数学 三年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 00:00:00 | ||
图片预览





文档简介
5.面积 单元测评卷 人教版数学 三年级下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在下面括号填上合适的面积单位。
一部手机屏幕的面积约70( );一张课桌面的面积约是24( );
一枚邮票的面积约是4( );教室地面的面积约是60( )。
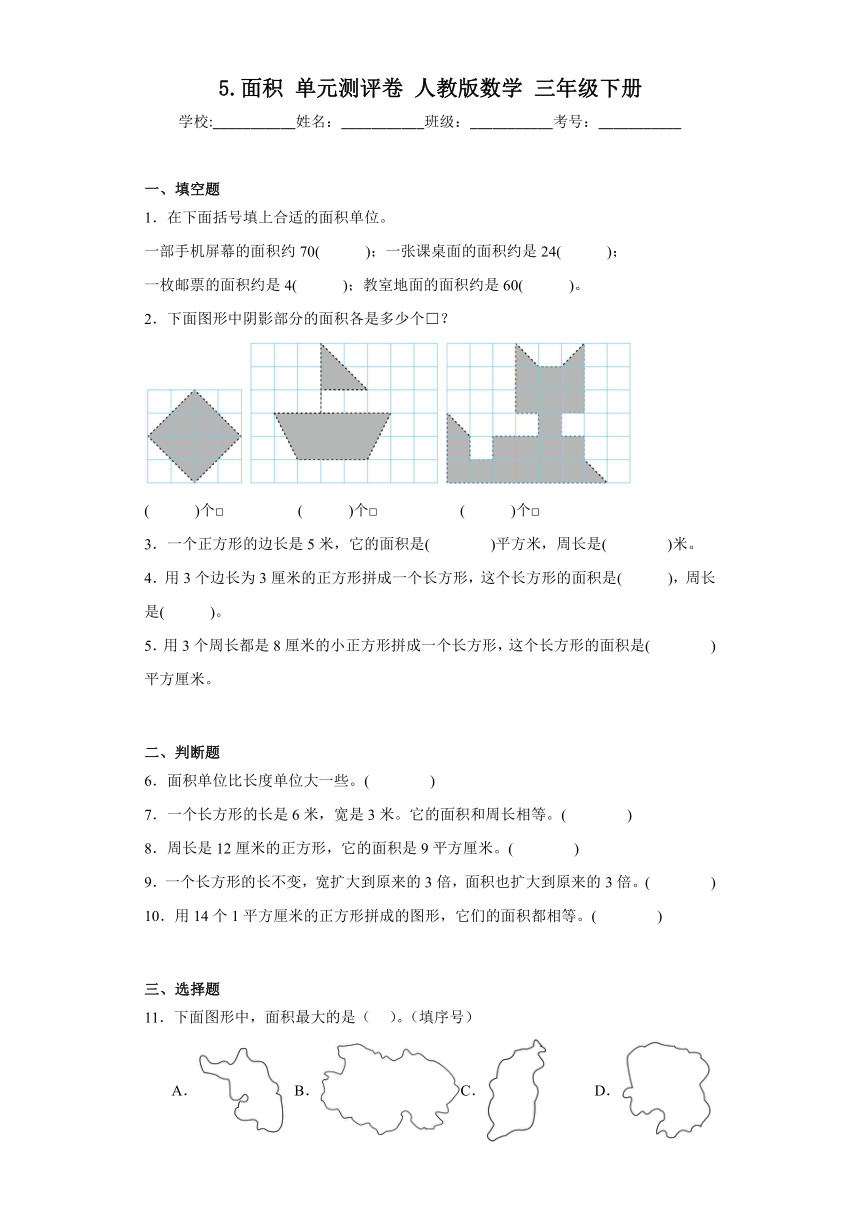
2.下面图形中阴影部分的面积各是多少个 ?
( )个□ ( )个□ ( )个□
3.一个正方形的边长是5米,它的面积是( )平方米,周长是( )米。
4.用3个边长为3厘米的正方形拼成一个长方形,这个长方形的面积是( ),周长是( )。
5.用3个周长都是8厘米的小正方形拼成一个长方形,这个长方形的面积是( )平方厘米。
二、判断题
6.面积单位比长度单位大一些。( )
7.一个长方形的长是6米,宽是3米。它的面积和周长相等。( )
8.周长是12厘米的正方形,它的面积是9平方厘米。( )
9.一个长方形的长不变,宽扩大到原来的3倍,面积也扩大到原来的3倍。( )
10.用14个1平方厘米的正方形拼成的图形,它们的面积都相等。( )
三、选择题
11.下面图形中,面积最大的是( )。(填序号)
A. B.C. D.
12.最接近1平方米的物品是( )。
A.大电视屏幕的面积 B.数学封面的面积
C.一间教室的面积 D.一块手帕的面积
13.根据图中所给的信息,整个大长方形的面积是( )平方厘米。
A.20 B.120 C.140 D.240
14.如图是一块长方形绿地,现在需要将绿地面积扩大到原来的6倍,长或宽可以如何变化?下面有( )位同学的说法正确。
松松:如果绿地的长不变,那么宽要扩大到原来的6倍。
奇奇:如果绿地的宽不变,那么长要扩大到原来的6倍。
萌萌:如果绿地的长不变,那么宽要增加55米。
欢欢:如果绿地的宽扩大到原来的3倍,那么长也要扩大到原来的3倍。
A.2 B.3 C.4 D.1
15.把4个边长是2cm的正方形拼成一个长方形,这个长方形的面积是( )。
A.4cm2 B.8cm2 C.12cm2 D.16cm2
四、作图题
16.下图是小明设计的图形,请你在方格纸上设计一个面积相等、形状不同的图形。
五、计算题
17.计算下面图形的面积。
六、解答题
18.清明上河图是中国十大传世名画之一,现藏于北京故宫博物馆。清明上河图长约53分米,宽约2分米。清明上河图的面积大约是多少平方分米?
19.一辆洒水车,每分钟行驶200米,洒水的宽度是10米。洒水车行驶8分钟,给多大的地面洒上水?
20.下面是公园的一面墙,每块青砖的长是4分米,宽是2分米。这个墙面的面积是多少平方米?
21.请你分别计算出卧室、书房、卫生间、厨房和客厅的面积。(单位:米)
22.2023年中央一号文件首提“和美乡村”,强调要扎实推进宜居宜业和美乡村建设。某村原计划建设一个宽是9米、面积是378平方米的长方形绿化带,现在需要扩建,如果长不变,宽增加27米,扩大后的面积是多少平方米?
参考答案:
1. 平方厘米/cm2 平方分米/dm2 平方厘米/cm2 平方米/m2
【分析】根据生活经验以及对面积单位和数据大小的认识,可知计量手机屏幕的面积,用平方厘米作单位;计量课桌面的面积,用平方分米作单位;计量一枚邮票的面积,用平方厘米作单位;计量教室地面的面积,用平方米作单位。
【详解】一部手机屏幕的面积约70平方厘米;
一张课桌面的面积约是24平方分米;
一枚邮票的面积约是4平方厘米;
教室地面的面积约是60平方米。
2. 8 10 20
【分析】左边图形中有4个□和8个半格,面积等于(4+8÷2)个□的面积和;中间图形中有9个□和2个半格,面积等于(9+2÷2)个□的面积和;右边图形中有18个□和4个半格,面积等于(18+4÷2)个□的面积和,据此作答。
【详解】4+8÷2
=4+4
=8
9+2÷2
=9+1
=10
18+4÷2
=18+2
=20
所以左边图形有8个□,中间图形有10个□,右边图形有20个□。
3. 25 20
【分析】根据正方形的面积=边长×边长,正方形的周长=边长×4,已知正方形的边长,代入数据,即可解答。
【详解】5×5=25(平方米)
5×4=20(米)
即一个正方形的边长是5米,它的面积是(25)平方米,周长是(20)米。
4. 27平方厘米 24厘米
【分析】用3个正方形拼成一个长方形,这个长方形的长为3×3=9(厘米),宽为3厘米,根据长方形的面积=长×宽,长方形的周长=(长+宽)×2,代入数值计算即可。
【详解】长方形的长为:3×3=9(厘米)
长方形的面积为:9×3=27(平方厘米)
长方形的周长为:
(9+3)×2
=12×2
=24(厘米)
这个长方形的面积是27平方厘米,周长是24厘米。
5.12
【分析】根据正方形的周长=边长×4,可知小正方形的边长为:8÷4=2(厘米),所以所拼长方形的长为2×3=6(厘米)、宽为2厘米,然后再利用长方形面积=长×宽,代入数据计算即可解答。
【详解】如图:
正方形的边长:8÷4=2(厘米)
长方形的长:2×3=6(厘米)
6×2=12(平方厘米)
因此,这个长方形的面积是12平方厘米。
6.×
【分析】面积单位计量物体的面积大小,长度单位计量物体的长度大小,两个单位不能互相比较,据此判断。
【详解】因为面积单位和长度单位不能互相比较,所以面积单位比长度单位大一些这种说法是错误的。
故答案为:×
【点睛】本题考查面积单位和长度单位的认识,面积单位之间比较大小,长度单位之间比较大小,但面积单位和长度单位不能比较大小。
7.×
【分析】根据周长、面积的意义,围成封闭图形一周的长叫做图形的周长;围成平面的大小叫做图形的面积。因为周长和面积不是同类量,所以无法进行比较。据此解答。
【详解】因为周长和面积不是同类量,所以长方形的面积和周长无法进行比较;故原题的说法错误。
故答案为:×
8.√
【分析】根据正方形的周长=边长×4,那么边长=周长÷4,据此求出边长,再根据正方形的面积公式=边长×边长,把数据代入公式求出它的面积与9平方厘米进行比较,即可解题。
【详解】12÷4=3(厘米)
3×3=9(平方厘米)
所以它的面积是9平方厘米,原题说法正确。
故答案为:√
【点睛】此题主要考查正方形的周长公式、面积公式的灵活运用,关键是熟记公式。
9.√
【分析】根据长方形的面积公式:S=ab,将长方形的宽扩大到原来的3倍,长不变,根据积的变化规律,一个因数不变,另一个因数扩大3倍,积也扩大3倍,由此解答。
【详解】根据分析,一个长方形的长不变,宽扩大到原来的3倍,所以,面积也扩大到原来的3倍;原题说法正确。
故答案为:√
【点睛】此题主要根据长方形的面积公式以及因数与积的变化规律解决问题。
10.√
【分析】根据题意,因为小正方形的面积都是1平方厘米,所以组合起来的大图形,无论形状如何,它们的面积都是相等的,据此解答。
【详解】(平方厘米)
用14个1平方厘米的正方形拼成的图形,它们的面积都相等。
故答案为:√
【点睛】这是组合图形的面积的题,学生要知道组合图形的面积就是小图形的面积之和。
11.B
【分析】物体的表面或围成的平面图形的大小,叫做它们的面积,根据面积的意义直接判断。
【详解】比较面积的大小的常用的方法,本题用眼睛观察直接比较即可得出B选项面积最大。
故答案为:B
12.A
【分析】边长是1米的正方形面积是1平方米,1平方米大约是一块大地板砖面积;边长是1分米的正方形面积是1平方分米,1平方分米大约是成人手掌大小;边长是1厘米的正方形面积是1平方厘米,1平方厘米大约是大指甲盖的大小。据此解答即可。
【详解】A.大电视屏幕的面积大约是1平方米,符合;
B.数学封面的面积大约是5平方分米,不符合;
C.一间教室的面积大约是50平方米,不符合;
D.一块手帕的面积大约是4平方分米,不符合。
即最接近1平方米的物品是大电视屏幕的面积。
故答案为:A
13.D
【分析】根据图示可知,大长方形的长是4个5厘米,宽为3个4厘米,长方形的面积=长×宽,依此计算并选择即可。
【详解】4×5=20(厘米)
4×3=12(厘米)
20×12=240(平方厘米)
整个大长方形的面积是240平方厘米。
故答案为:D
【点睛】此题考查的是长方形面积的计算,先计算出长方形的长和宽,是解答此题的关键。
14.B
【分析】原来长方形绿地的面积=长×宽,扩大后绿地的面积为长×宽×6,即为原来绿地面积×6,根据长方形面积=长×宽,分别计算出四位同学的方案中绿地的面积,即可得出结论。
【详解】原来绿地的面积=长×宽=22×11,
松松:长不变,宽扩大到原来的6倍,现在的面积=长×(宽×6)=原来的面积×6,
即:绿地面积扩大到原来的6倍,松松说法正确;
奇奇:宽不变,长要扩大到原来的6倍,现在的面积=(长×6)×宽=原来的面积×6,
即:绿地面积扩大到原来的6倍,奇奇说法正确;
萌萌:宽要增加55米。11+55=66(米)
66÷11=6,相当于长不变,宽扩大到原来的6倍,
现在的面积=长×(宽×6)=原来的面积×6,
即:绿地面积扩大到原来的6倍,萌萌说法正确;
欢欢:绿地的宽扩大到原来的3倍,那么长也要扩大到原来的3倍,
(长×3)×(宽×3)=长×宽×9=原来的面积×9,
即:绿地面积扩大到原来的9倍,不是6倍,欢欢说法错误;
由此可知,上面有3位同学的说法正确。
故答案为:B
【点睛】解决本题关键是熟练掌握长方形的面积公式,并且能够灵活的运用。
15.D
【分析】要用4个边长是2cm的正方形拼成一个长方形, 可以4个排成一排,先求出拼接得到的长方形的长和宽,再根据长方形的面积公式等于长乘宽即可得到答案。
【详解】拼接得到的长方形长为:2+2+2+2=8cm,宽为:2cm
面积为:8×2=16cm2
故答案为:D
16.见详解
【分析】根据图示,小明设计的图形占7格,所以所画图形也应该占7格。利用长方形面积=长×宽,可知7=7×1,可以画一个长7格、宽1格的长方形即可,答案不唯一。
【详解】据分析作图如下:
(答案不唯一)
【点睛】本题考查了画指定面积图形的方法,解答此题的关键是熟练掌握长方形的面积公式,然后再确定图形的长和宽,最后进行作图即可。
17.(1)45平方厘米
(2)4050平方米
【分析】长方形的面积=长×宽,直接将长方形的长和宽的长度代入公式计算即可。
【详解】(1)5×9=45(平方厘米)
(2)45×90=4050(平方米)
18.106平方分米
【分析】根据长方形面积=长×宽,代入长宽的数值,列式求解。
【详解】53×2=106(平方分米)
答:清明上河图的面积大约是106平方分米。
19.16000平方米
【分析】根据题意可知,所洒地面是一个长方形,首先根据速度×时间=路程,求出8分钟洒水车行驶多少米(也就是所洒地面长方形的长),已知洒水的宽度是10米,利用长方形的面积公式解答即可。
【详解】200×8×10
=1600×10
=16000(平方米)
答:给16000平方米的地面洒上水。
20.4平方米
【分析】长方形面积=长×宽,根据题意可知,每面墙一共有(10×5)块青砖,每块青砖的面积为(4×2)平方分米,用每块青砖的面积乘青砖的块数即为每面墙的面积,再根据1平方米=100平方分米,据此解答即可。
【详解】4×2×10×5
=8×10×5
=80×5
=400(平方分米)
400平方分米=4平方米
答:这个墙面的面积是4平方米。
21.25平方米,30平方米,6平方米,4平方米,34平方米
【分析】根据题图可知,卧室是个边长为5米的正方形,根据正方形的面积=边长×边长,代入数据,即可求出卧室的面积;书房是一个长为6米,宽为5米的长方形,根据长方形的面积=长×宽,代入数据,即可求出书房的面积;卫生间是一个长为3米,宽为2米的长方形,根据长方形的面积=长×宽,代入数据,即可求出卫生间的面积;厨房是个边长为2米的正方形,根据正方形的面积=边长×边长,代入数据,即可求出厨房的面积;客厅的面积等于长为(5+6)米,宽为4米的长方形的面积减去卫生间和厨房的面积,根据长方形的面积=长×宽以及前面算出的卫生间和厨房的面积,即可求出客厅的面积;据此列式计算即可解答。
【详解】卧室的面积:5×5=25(平方米)
书房的面积:5×6=30(平方米)
卫生间的面积:2×3=6(平方米)
厨房的面积:2×2=4(平方米)
客厅的面积:(5+6)×4-6-4
=11×4-6-4
=44-6-4
=38-4
=34(平方米)
答:卧室、书房、卫生间、厨房和客厅的面积分别是:25平方米、30平方米、6平方米、4平方米和34平方米。
22.1512平方米
【分析】因为“长×宽=长方形面积”,所以,当长不变,宽增加时,可以利用积的变化规律进行解题。
积的变化规律:一个因数不变,另一个因数乘或除以一个不为0的数,积也乘或除以这个数。
因此需要先用“原来的宽+增加的长度”求出扩建后的宽是多长;再用“扩建后的宽÷原来的宽”,商是几,现在的宽就是原来的宽乘几得到的;最后根据积的变化规律用“原来的面积×几”,即可算出扩大后的面积。
【详解】(27+9)÷9
=36÷9
=4
378×4=1512(平方米)
答:扩大后的面积是1512平方米。
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在下面括号填上合适的面积单位。
一部手机屏幕的面积约70( );一张课桌面的面积约是24( );
一枚邮票的面积约是4( );教室地面的面积约是60( )。
2.下面图形中阴影部分的面积各是多少个 ?
( )个□ ( )个□ ( )个□
3.一个正方形的边长是5米,它的面积是( )平方米,周长是( )米。
4.用3个边长为3厘米的正方形拼成一个长方形,这个长方形的面积是( ),周长是( )。
5.用3个周长都是8厘米的小正方形拼成一个长方形,这个长方形的面积是( )平方厘米。
二、判断题
6.面积单位比长度单位大一些。( )
7.一个长方形的长是6米,宽是3米。它的面积和周长相等。( )
8.周长是12厘米的正方形,它的面积是9平方厘米。( )
9.一个长方形的长不变,宽扩大到原来的3倍,面积也扩大到原来的3倍。( )
10.用14个1平方厘米的正方形拼成的图形,它们的面积都相等。( )
三、选择题
11.下面图形中,面积最大的是( )。(填序号)
A. B.C. D.
12.最接近1平方米的物品是( )。
A.大电视屏幕的面积 B.数学封面的面积
C.一间教室的面积 D.一块手帕的面积
13.根据图中所给的信息,整个大长方形的面积是( )平方厘米。
A.20 B.120 C.140 D.240
14.如图是一块长方形绿地,现在需要将绿地面积扩大到原来的6倍,长或宽可以如何变化?下面有( )位同学的说法正确。
松松:如果绿地的长不变,那么宽要扩大到原来的6倍。
奇奇:如果绿地的宽不变,那么长要扩大到原来的6倍。
萌萌:如果绿地的长不变,那么宽要增加55米。
欢欢:如果绿地的宽扩大到原来的3倍,那么长也要扩大到原来的3倍。
A.2 B.3 C.4 D.1
15.把4个边长是2cm的正方形拼成一个长方形,这个长方形的面积是( )。
A.4cm2 B.8cm2 C.12cm2 D.16cm2
四、作图题
16.下图是小明设计的图形,请你在方格纸上设计一个面积相等、形状不同的图形。
五、计算题
17.计算下面图形的面积。
六、解答题
18.清明上河图是中国十大传世名画之一,现藏于北京故宫博物馆。清明上河图长约53分米,宽约2分米。清明上河图的面积大约是多少平方分米?
19.一辆洒水车,每分钟行驶200米,洒水的宽度是10米。洒水车行驶8分钟,给多大的地面洒上水?
20.下面是公园的一面墙,每块青砖的长是4分米,宽是2分米。这个墙面的面积是多少平方米?
21.请你分别计算出卧室、书房、卫生间、厨房和客厅的面积。(单位:米)
22.2023年中央一号文件首提“和美乡村”,强调要扎实推进宜居宜业和美乡村建设。某村原计划建设一个宽是9米、面积是378平方米的长方形绿化带,现在需要扩建,如果长不变,宽增加27米,扩大后的面积是多少平方米?
参考答案:
1. 平方厘米/cm2 平方分米/dm2 平方厘米/cm2 平方米/m2
【分析】根据生活经验以及对面积单位和数据大小的认识,可知计量手机屏幕的面积,用平方厘米作单位;计量课桌面的面积,用平方分米作单位;计量一枚邮票的面积,用平方厘米作单位;计量教室地面的面积,用平方米作单位。
【详解】一部手机屏幕的面积约70平方厘米;
一张课桌面的面积约是24平方分米;
一枚邮票的面积约是4平方厘米;
教室地面的面积约是60平方米。
2. 8 10 20
【分析】左边图形中有4个□和8个半格,面积等于(4+8÷2)个□的面积和;中间图形中有9个□和2个半格,面积等于(9+2÷2)个□的面积和;右边图形中有18个□和4个半格,面积等于(18+4÷2)个□的面积和,据此作答。
【详解】4+8÷2
=4+4
=8
9+2÷2
=9+1
=10
18+4÷2
=18+2
=20
所以左边图形有8个□,中间图形有10个□,右边图形有20个□。
3. 25 20
【分析】根据正方形的面积=边长×边长,正方形的周长=边长×4,已知正方形的边长,代入数据,即可解答。
【详解】5×5=25(平方米)
5×4=20(米)
即一个正方形的边长是5米,它的面积是(25)平方米,周长是(20)米。
4. 27平方厘米 24厘米
【分析】用3个正方形拼成一个长方形,这个长方形的长为3×3=9(厘米),宽为3厘米,根据长方形的面积=长×宽,长方形的周长=(长+宽)×2,代入数值计算即可。
【详解】长方形的长为:3×3=9(厘米)
长方形的面积为:9×3=27(平方厘米)
长方形的周长为:
(9+3)×2
=12×2
=24(厘米)
这个长方形的面积是27平方厘米,周长是24厘米。
5.12
【分析】根据正方形的周长=边长×4,可知小正方形的边长为:8÷4=2(厘米),所以所拼长方形的长为2×3=6(厘米)、宽为2厘米,然后再利用长方形面积=长×宽,代入数据计算即可解答。
【详解】如图:
正方形的边长:8÷4=2(厘米)
长方形的长:2×3=6(厘米)
6×2=12(平方厘米)
因此,这个长方形的面积是12平方厘米。
6.×
【分析】面积单位计量物体的面积大小,长度单位计量物体的长度大小,两个单位不能互相比较,据此判断。
【详解】因为面积单位和长度单位不能互相比较,所以面积单位比长度单位大一些这种说法是错误的。
故答案为:×
【点睛】本题考查面积单位和长度单位的认识,面积单位之间比较大小,长度单位之间比较大小,但面积单位和长度单位不能比较大小。
7.×
【分析】根据周长、面积的意义,围成封闭图形一周的长叫做图形的周长;围成平面的大小叫做图形的面积。因为周长和面积不是同类量,所以无法进行比较。据此解答。
【详解】因为周长和面积不是同类量,所以长方形的面积和周长无法进行比较;故原题的说法错误。
故答案为:×
8.√
【分析】根据正方形的周长=边长×4,那么边长=周长÷4,据此求出边长,再根据正方形的面积公式=边长×边长,把数据代入公式求出它的面积与9平方厘米进行比较,即可解题。
【详解】12÷4=3(厘米)
3×3=9(平方厘米)
所以它的面积是9平方厘米,原题说法正确。
故答案为:√
【点睛】此题主要考查正方形的周长公式、面积公式的灵活运用,关键是熟记公式。
9.√
【分析】根据长方形的面积公式:S=ab,将长方形的宽扩大到原来的3倍,长不变,根据积的变化规律,一个因数不变,另一个因数扩大3倍,积也扩大3倍,由此解答。
【详解】根据分析,一个长方形的长不变,宽扩大到原来的3倍,所以,面积也扩大到原来的3倍;原题说法正确。
故答案为:√
【点睛】此题主要根据长方形的面积公式以及因数与积的变化规律解决问题。
10.√
【分析】根据题意,因为小正方形的面积都是1平方厘米,所以组合起来的大图形,无论形状如何,它们的面积都是相等的,据此解答。
【详解】(平方厘米)
用14个1平方厘米的正方形拼成的图形,它们的面积都相等。
故答案为:√
【点睛】这是组合图形的面积的题,学生要知道组合图形的面积就是小图形的面积之和。
11.B
【分析】物体的表面或围成的平面图形的大小,叫做它们的面积,根据面积的意义直接判断。
【详解】比较面积的大小的常用的方法,本题用眼睛观察直接比较即可得出B选项面积最大。
故答案为:B
12.A
【分析】边长是1米的正方形面积是1平方米,1平方米大约是一块大地板砖面积;边长是1分米的正方形面积是1平方分米,1平方分米大约是成人手掌大小;边长是1厘米的正方形面积是1平方厘米,1平方厘米大约是大指甲盖的大小。据此解答即可。
【详解】A.大电视屏幕的面积大约是1平方米,符合;
B.数学封面的面积大约是5平方分米,不符合;
C.一间教室的面积大约是50平方米,不符合;
D.一块手帕的面积大约是4平方分米,不符合。
即最接近1平方米的物品是大电视屏幕的面积。
故答案为:A
13.D
【分析】根据图示可知,大长方形的长是4个5厘米,宽为3个4厘米,长方形的面积=长×宽,依此计算并选择即可。
【详解】4×5=20(厘米)
4×3=12(厘米)
20×12=240(平方厘米)
整个大长方形的面积是240平方厘米。
故答案为:D
【点睛】此题考查的是长方形面积的计算,先计算出长方形的长和宽,是解答此题的关键。
14.B
【分析】原来长方形绿地的面积=长×宽,扩大后绿地的面积为长×宽×6,即为原来绿地面积×6,根据长方形面积=长×宽,分别计算出四位同学的方案中绿地的面积,即可得出结论。
【详解】原来绿地的面积=长×宽=22×11,
松松:长不变,宽扩大到原来的6倍,现在的面积=长×(宽×6)=原来的面积×6,
即:绿地面积扩大到原来的6倍,松松说法正确;
奇奇:宽不变,长要扩大到原来的6倍,现在的面积=(长×6)×宽=原来的面积×6,
即:绿地面积扩大到原来的6倍,奇奇说法正确;
萌萌:宽要增加55米。11+55=66(米)
66÷11=6,相当于长不变,宽扩大到原来的6倍,
现在的面积=长×(宽×6)=原来的面积×6,
即:绿地面积扩大到原来的6倍,萌萌说法正确;
欢欢:绿地的宽扩大到原来的3倍,那么长也要扩大到原来的3倍,
(长×3)×(宽×3)=长×宽×9=原来的面积×9,
即:绿地面积扩大到原来的9倍,不是6倍,欢欢说法错误;
由此可知,上面有3位同学的说法正确。
故答案为:B
【点睛】解决本题关键是熟练掌握长方形的面积公式,并且能够灵活的运用。
15.D
【分析】要用4个边长是2cm的正方形拼成一个长方形, 可以4个排成一排,先求出拼接得到的长方形的长和宽,再根据长方形的面积公式等于长乘宽即可得到答案。
【详解】拼接得到的长方形长为:2+2+2+2=8cm,宽为:2cm
面积为:8×2=16cm2
故答案为:D
16.见详解
【分析】根据图示,小明设计的图形占7格,所以所画图形也应该占7格。利用长方形面积=长×宽,可知7=7×1,可以画一个长7格、宽1格的长方形即可,答案不唯一。
【详解】据分析作图如下:
(答案不唯一)
【点睛】本题考查了画指定面积图形的方法,解答此题的关键是熟练掌握长方形的面积公式,然后再确定图形的长和宽,最后进行作图即可。
17.(1)45平方厘米
(2)4050平方米
【分析】长方形的面积=长×宽,直接将长方形的长和宽的长度代入公式计算即可。
【详解】(1)5×9=45(平方厘米)
(2)45×90=4050(平方米)
18.106平方分米
【分析】根据长方形面积=长×宽,代入长宽的数值,列式求解。
【详解】53×2=106(平方分米)
答:清明上河图的面积大约是106平方分米。
19.16000平方米
【分析】根据题意可知,所洒地面是一个长方形,首先根据速度×时间=路程,求出8分钟洒水车行驶多少米(也就是所洒地面长方形的长),已知洒水的宽度是10米,利用长方形的面积公式解答即可。
【详解】200×8×10
=1600×10
=16000(平方米)
答:给16000平方米的地面洒上水。
20.4平方米
【分析】长方形面积=长×宽,根据题意可知,每面墙一共有(10×5)块青砖,每块青砖的面积为(4×2)平方分米,用每块青砖的面积乘青砖的块数即为每面墙的面积,再根据1平方米=100平方分米,据此解答即可。
【详解】4×2×10×5
=8×10×5
=80×5
=400(平方分米)
400平方分米=4平方米
答:这个墙面的面积是4平方米。
21.25平方米,30平方米,6平方米,4平方米,34平方米
【分析】根据题图可知,卧室是个边长为5米的正方形,根据正方形的面积=边长×边长,代入数据,即可求出卧室的面积;书房是一个长为6米,宽为5米的长方形,根据长方形的面积=长×宽,代入数据,即可求出书房的面积;卫生间是一个长为3米,宽为2米的长方形,根据长方形的面积=长×宽,代入数据,即可求出卫生间的面积;厨房是个边长为2米的正方形,根据正方形的面积=边长×边长,代入数据,即可求出厨房的面积;客厅的面积等于长为(5+6)米,宽为4米的长方形的面积减去卫生间和厨房的面积,根据长方形的面积=长×宽以及前面算出的卫生间和厨房的面积,即可求出客厅的面积;据此列式计算即可解答。
【详解】卧室的面积:5×5=25(平方米)
书房的面积:5×6=30(平方米)
卫生间的面积:2×3=6(平方米)
厨房的面积:2×2=4(平方米)
客厅的面积:(5+6)×4-6-4
=11×4-6-4
=44-6-4
=38-4
=34(平方米)
答:卧室、书房、卫生间、厨房和客厅的面积分别是:25平方米、30平方米、6平方米、4平方米和34平方米。
22.1512平方米
【分析】因为“长×宽=长方形面积”,所以,当长不变,宽增加时,可以利用积的变化规律进行解题。
积的变化规律:一个因数不变,另一个因数乘或除以一个不为0的数,积也乘或除以这个数。
因此需要先用“原来的宽+增加的长度”求出扩建后的宽是多长;再用“扩建后的宽÷原来的宽”,商是几,现在的宽就是原来的宽乘几得到的;最后根据积的变化规律用“原来的面积×几”,即可算出扩大后的面积。
【详解】(27+9)÷9
=36÷9
=4
378×4=1512(平方米)
答:扩大后的面积是1512平方米。
