8.1成对数据的相关分析 同步练习(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册
文档属性
| 名称 | 8.1成对数据的相关分析 同步练习(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 22:21:35 | ||
图片预览



文档简介
8.1成对数据的相关分析同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有以下几组的统计数据:要使剩下的数据具有较强的相关关系,应去掉的一组数据是( )
A. B. C. D.
2.在一元线性回归模型中,设变量和变量的样本相关系数为,决定系数为,变量和变量的样本相关系数为,决定系数为,且,,则( )
A.和之间呈正线性相关关系,且
B.和之间呈负线性相关关系,且
C.和之间呈负线性相关关系,且
D.和之间呈正线性相关关系,且
3.已知变量和满足关系,变量y与正相关,则( )
A.与负相关,与负相关 B.与正相关,与正相关
C.与正相关,与负相关 D.与负相关,与正相关
4.已知关于变量有相关关系,由观测数据得到的样本数据散点图如图所示,则该组观测数据中关于的回归方程可能是( )
A. B.
C. D.
5.对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较,下列结论正确的是( )
A. B.
C. D.
6.对四组数据进行统计,获得如下散点图,关于其相关系数的比较,说法正确的是( )
A. B.
C. D.
7.2003年春季,我国部分地区SARS流行,党和政府采取果断措施,防治结合,很快使病情得到控制,下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据,以及根据这些数据绘制出的散点图
日期 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10 5.11 5.12
人数 100 109 115 118 121 134 141 152 168 175 186 203
下列说法:①根据此散点图,可以判断日期与人数具有线性相关关系;②根据此散点图,可以判断日期与人数具有一次函数关系.其中正确的个数为( )
A.0个 B.1个 C.2个 D.以上都不对
8.相关变量x,y的散点图如图所示,现对这两个变量进行线性相关分析.方案一:根据图中所有数据,得到回归直线方程,相关系数为;方案二:剔除点,根据剩下的数据得到回归直线方程,相关系数为.则( )
A. B.
C. D.
二、多选题
9.下列命题正确的是( )
A.已知,若,则
B.若散点图的散点均落在一条斜率非0的直线上,则决定系数
C.数据的均值为4,标准差为1,则这组数据中没有大于5的数
D.数据的75百分位数为47
10.某市7天国庆节假期期间的楼房日认购量(单位:套)与日成交量(单位:套)的折线图如下图所示,小明同学根据折线图对这7天的日认购量与日成交量作出如下判断,则下列结论正确的是( )
A.日认购量与日期正相关
B.日成交量的中位数是26
C.日成交量超过日平均成交量的有2天
D.10月7日日认购量的增量大于10月7日日成交量的增量
11.对于下列概率统计相关知识,说法正确的是( )
A.数据1,2,3,4,5,6,8,9,11的第75百分位数是7
B.若事件M,N的概率满足,且M,N相互独立,则
C.由两个分类变量,的成对样本数据计算得到,依据的独立性检验,可判断,独立
D.若一组样本数据的对应样本点都在直线上,则这组样本数据的相关系数为
12.(多选)某中学的兴趣小组在某座山测得海拔高度、气压和沸点的六组数据绘制成散点图如图所示,则下列说法正确的是( )
A.沸点与海拔高度呈正相关
B.沸点与气压呈正相关
C.沸点与海拔高度呈负相关
D.气压与海拔高度呈负相关
三、填空题
13.垃圾分类是保护环境,改善人居环境、促进城市精细化管理、保障可持续发展的重要举措.某小区为了倡导居民对生活垃圾进行分类,对垃圾分类后处理垃圾(千克)所需的费用(角)的情况作了调研,并统计得到表中几组对应数据,同时用最小二乘法得到关于的线性回归方程为,则下列正确说法的序号是 .
2 3 4 5
2 2.3 3.4
①变量之间呈正相关关系;
②可以预测当时,的值为6.88;
③表中的值为3.9;
④样本中心点为.
14.在线性回归分析中,常用作为衡量模拟效果的一个指标.
下面关于的说法:①越大,说明模型拟合的效果越好;
②越接近1,说明回归的效果越好;
③越接近1,说明回归的效果越差.请你写出所有正确说法的序号 .
15.观察下列散点图,具有相关关系的是 (填序号).
16.对变量x、y有观测数据(i=1,2,…,10),得散点图如图1所示;对变量u、v有观测数据(i=1,2,…,10),得散点图如图2所示.由这两个散点图函可以判断变量x与y ,u与v .(填写“正相关”或“负相关”)
四、解答题
17.将保护区分为面积大小相近的多个区域,用简单随机抽样的方法抽取其中15个区域进行编号,统计抽取到每个区域的某种水源指标和区域内该植物分布的数量(,2,…,15),得到数组.已知,,.
(1)求样本(,2…,15)的相关系数;
(2)假设该植物的寿命为随机变量X(X可取任意正整数).研究人员统计大量数据后发现:对于任意的,寿命为的样本在寿命超过k的样本里的数量占比与寿命为1的样本在全体样本中的数量占比相同,均等于0.1,这种现象被称为“几何分布的无记忆性”.
(ⅰ)求()的表达式;
(ⅱ)推导该植物寿命期望的值.
附:相关系数.
18.某校数学建模学生社团进行了一项实验研究,采集了的一组数据如下表所示:
2 3 4 5 6 7
52.5 45 40 30 25 17.5
该社团对上述数据进行了分析,发现与之间具有线性相关关系.
(1)画出表中数据的散点图,并指出与之间的相关系数是正还是负;
(2)求出关于的线性回归方程,并写出当时,预测数据的值.
附:在线性回归方程中,,其中为样本平均值.
19.党的二十大以来,国家不断加大对科技创新的支持力度,极大鼓舞了企业持续投入研发的信心.某科技企业在国家一系列优惠政策的大力扶持下,通过不断的研发和技术革新,提升了企业收益水平.下表是对2023 年1 ~5月份该企业的利润y(单位:百万)的统计.
月份 1 月 2 月 3 月 4 月 5 月
月份编号x 1 2 3 4 5
利润y(百万) 7 12 13 19 24
(1)根据统计表,求该企业的利润y与月份编号x的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(,则认为y与x的线性相关性较强,,则认为y与x的线性相关性较弱.);
(2)该企业现有甲、乙两条流水线生产同一种产品.为对产品质量进行监控,质检人员先用简单随机抽样的方法从甲、乙两条流水线上分别抽取了5件、3件产品进行初检,再从中随机选取3件做进一步的质检,记抽到“甲流水线产品”的件数为,试求的分布列与期望.
附:相关系数
20.新冠病毒奥密克戎毒株开始流行后,为了控制新冠肺炎疫情,杭州某高中开展了每周核酸检测工作.周一至周五,每天中午13:30开始,安排位师生进行核酸检测,教职工每天都要检测,用五天时间实现全员覆盖.
(1)该校教职工有人,高二学生有人,高三学生有人.
①用分层抽样的方法,求高一学生每天的检测人数.
②高一年级共个班,该年级每天进行核酸检测的学生有两种安排方案.方案一:集中来自部分班级;方案二:分散来自所有班级.你认为哪种方案更合理?给出理由.
(2)学校开展核酸检测的第一周,周一至周五核酸检测用时记录如下表.
第天
用时
①计算变量和的相关系数(精确到),并说明两变量的线性相关程度;
②根据①中的计算结果,判定变量和是正相关还是负相关,并给出可能的原因.
参考数据和公式:,相关系数.
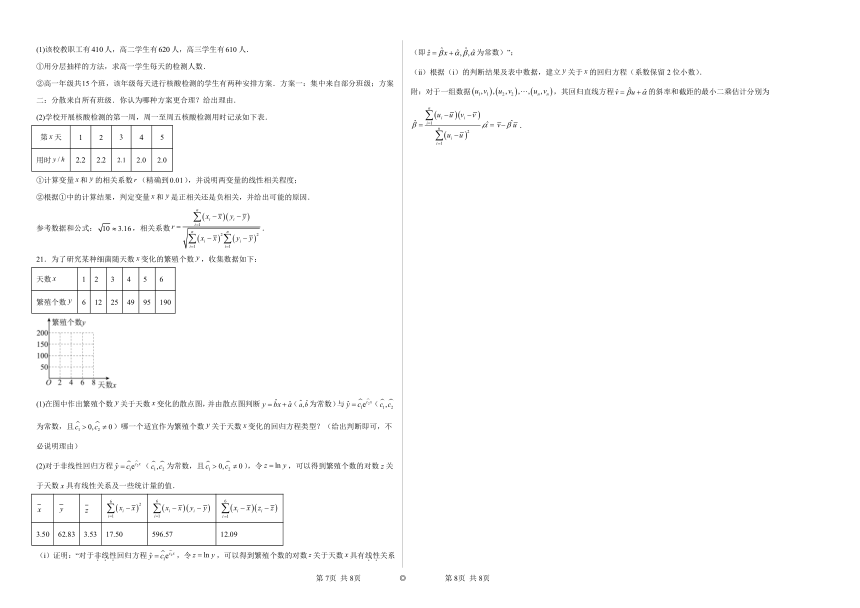
21.为了研究某种细菌随天数变化的繁殖个数,收集数据如下:
天数 1 2 3 4 5 6
繁殖个数 6 12 25 49 95 190
(1)在图中作出繁殖个数关于天数变化的散点图,并由散点图判断(为常数)与(为常数,且)哪一个适宜作为繁殖个数关于天数变化的回归方程类型?(给出判断即可,不必说明理由)
(2)对于非线性回归方程(为常数,且),令,可以得到繁殖个数的对数z关于天数x具有线性关系及一些统计量的值.
3.50 62.83 3.53 17.50 596.57 12.09
(ⅰ)证明:“对于非线性回归方程,令,可以得到繁殖个数的对数关于天数具有线性关系(即为常数)”;
(ⅱ)根据(ⅰ)的判断结果及表中数据,建立关于的回归方程(系数保留2位小数).
附:对于一组数据,其回归直线方程的斜率和截距的最小二乘估计分别为.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
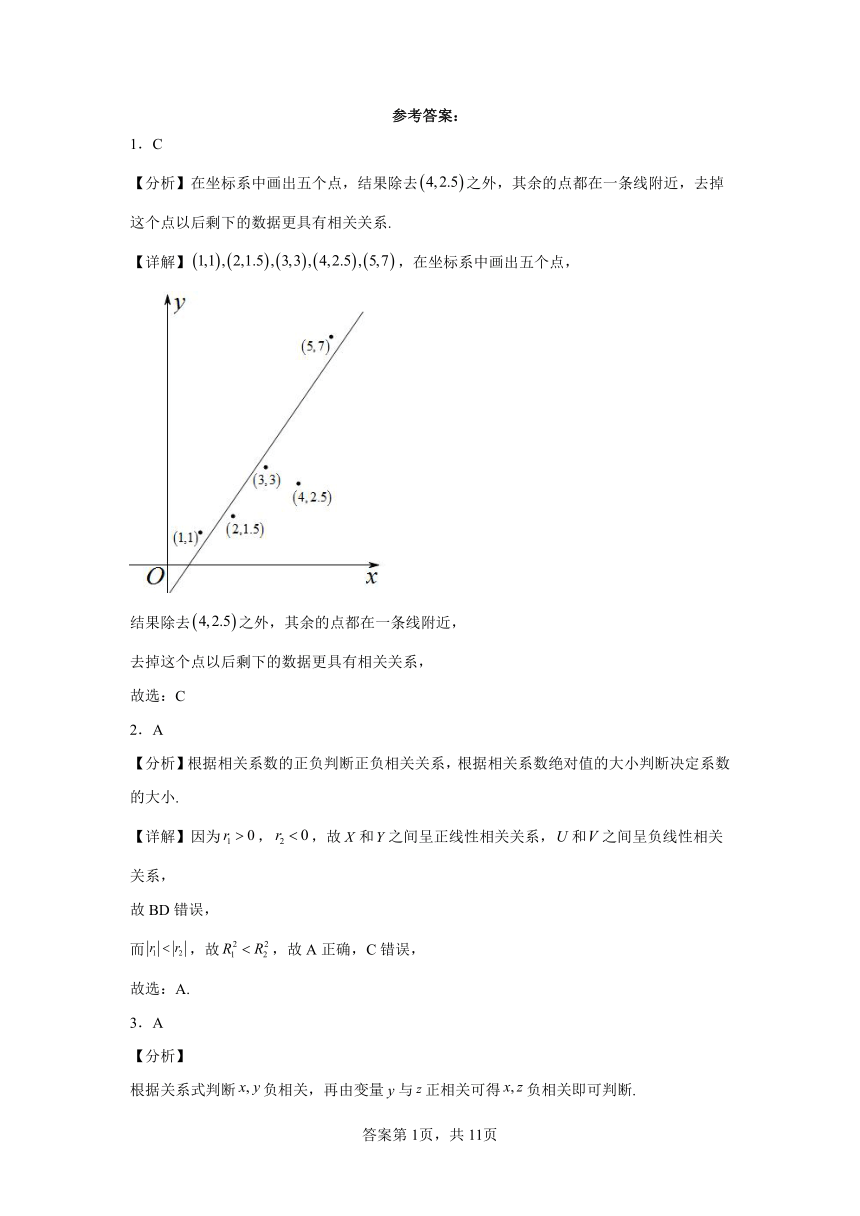
1.C
【分析】在坐标系中画出五个点,结果除去之外,其余的点都在一条线附近,去掉这个点以后剩下的数据更具有相关关系.
【详解】,在坐标系中画出五个点,
结果除去之外,其余的点都在一条线附近,
去掉这个点以后剩下的数据更具有相关关系,
故选:C
2.A
【分析】根据相关系数的正负判断正负相关关系,根据相关系数绝对值的大小判断决定系数的大小.
【详解】因为,,故和之间呈正线性相关关系,和之间呈负线性相关关系,
故BD错误,
而,故,故A正确,C错误,
故选:A.
3.A
【分析】
根据关系式判断负相关,再由变量y与正相关可得负相关即可判断.
【详解】因为变量和满足关系,变量y与正相关,
由正相关、负相关的定义可知与负相关,与负相关.
故选:A
4.D
【分析】根据数据散点图的单调性,结合选项中的函数,逐项判定,即可求解.
【详解】由散点图可知,所求回归方程先减后增,选项中A,B均为定义域上的增函数,不符合题意;
选项C中的函数图象为开口向下的抛物线,不符合题意;
而选项D中的函数图象增减性与散点图符合题意,故D正确.
故选:D.
5.B
【分析】根据散点图分析出样本的相关关系即可.
【详解】由给出的四组数据的散点图可以看出,
左侧两图是正相关,样本相关系数大于0,则,,
右侧两图是负相关,样本相关系数小于0,则,,
下方两图的点相对更加集中,所以相关性较强,所以接近于1,接近于-1,
上方两图的点相对分散一些,所以相关性较弱,所以和比较接近0,
由此可得.
故选:B.
6.B
【分析】
根据散点图的分布判断相关系数的符号和绝对值大小,即可得结果.
【详解】由图中散点的分布趋势知:,,
由图散点的分布状态知:,,
所以.
故选:B
7.B
【分析】
作出散点图即可得出结论.
【详解】由题意,
做出散点图如下图所示,
由图可知,
日期与人数具有线性相关关系,但不是一次函数关系,
①正确,②错误,
故选:B.
8.D
【分析】根据相关系数的意义:其绝对值越接近1,说明两个变量越具有线性相关,以及负相关的意义作判断即可.
【详解】由散点图可知这两个变量为负相关,所以.
因为剔除点后,剩下点的数据更具有线性相关性,更接近1,
所以 .
故选:D.
9.ABD
【分析】对于A:利用正态分布的对称性判断;对于B:根据相关的概念判断;对于C:举反例说明;对于D:直接求75百分位数.
【详解】对于A:已知,若,
则,A正确;
对于B:若散点图的散点均落在一条斜率非0的直线上,则变量与变量之间满足线性函数关系,则决定系数,B正确;
对于C:不妨设,
则,解得,
此时,
故找到一组数,数据中有大于5的数,C错误;
对于D:,故这组数据的75百分位数为47,D正确.
故选:ABD.
10.BD
【分析】
根据正相关的定义结合图象即可判断A;根据中位数的定义结合图象即可判断B;根据图中数据进行计算即可求得平均数,即可判断C;根据图中数据进行计算即可判断D.
【详解】由题图可以看出,数据点并不是从左下至右上分布,所以错;
将成交量数据按大小顺序排列,中位数为26,所以对;
日平均成交量为,
超过42.7的只有一天,所以错;
10月7日认购量的增量为,
成交量的增量为,所以对,
故选:BD.
11.BCD
【分析】根据百分位数的定义求出第75百分位数,从而判定A;由独立性得到,进而利用对立事件的概率关系判定B;根据,可判定C;根据直线方程斜率为负值,可知相关系数为负值,根据所有点都在直线上,可知相关系数绝对值为1,进而可知相关系数,从而判定D.
【详解】对于选项A,9个数据从小到大排列,由于,所以第75百分位数应该是第7个数8,故A错误;
对于选项B,由M,N相互独立得:,所以,,故B正确:
对于选项C,由,可以认为和独立,故C正确:
对于选项D,样本点都在直线,说明是负相关且为线性函数关系,所以相关系数为,故D正确,
故选:BCD.
12.BCD
【分析】
根据散点图的特点及正相关负相关的定义即可求解.
【详解】
由左图知气压随海拔高度的增加而减小,由右图知沸点随气压的升高而升高,
所以气压与海拔高度呈负相关,沸点与气压呈正相关,沸点与海拔高度呈负相关.
故选:BCD.
13.①②④
【分析】由,可得判定①正确;令时,求得,可判定②正确;根据回归直线方程的含义与性质,可判定③错误,④正确.
【详解】对于①中,由关于的线性回归方程为,可得,
所以变量之间呈正相关关系,所以①正确;
对于②中,由关于的线性回归方程为,
当时,可得,所以②正确;
对于③中,由表格中的数据,可得,,
可得,解得,所以③错误;
对于④中,由,,即样本中心点为,所以④正确.
故答案为:①②④.
14.①②
【分析】由线性回归中的意义即可得解.
【详解】在表达式中,与经验回归方程无关,残差平方后与经验回归方程有关,因此越大,表示残差平方后越小,即模型的拟合效果越好;越小,表示残差平方和越大,即模型的拟合效果越差,可知①②正确③错误.
故答案为:①②
15.②③
【分析】根据散点图中散点的分别规律,结合相关关系的定义,逐项判定,即可求解.
【详解】散点图①中,所以的散点都在曲线上,所以①具有函数关系,不符合题意;
散点图②中,所有的散点分布在一条直线的附近,所以②具有相关关系,符合题意;
散点图③中,所有散点都分布在一条曲线的附近,所以③具有相关关系,符合题意;
散点图④中,所有的散点杂乱无章,没有分布在一条曲线的附近,所以④不具有相关关系,不符合题意.
故答案为:②③
16. 负相关 正相关
【分析】根据散点图及正相关,负相关的概念即得.
【详解】由图1可知点散布在从左上角到右下角的区域,所以变量x与y负相关,
由图2可知点散布在从左下角到右上角的区域,所以变量u与v正相关.
故答案为:负相关;正相关.
17.(1)0.8;
(2)(ⅰ);(ⅱ)10.
【分析】(1)利用给定数据及相关系数公式计算即得.
(2)先根据递推关系得到与的关系,进而利用等比数列得到通项公式,推导出的表达式,最后得到的表达式,应用错位相减法求和即可.
【详解】(1)由,,,
得相关系数.
(2)(ⅰ)依题意,,又,
则,当时,把换成,则,
两式相减,得,即,
又,于是对任意都成立,
从而是首项为0.1,公比为0.9的等比数列,
所以;
(ⅱ)由定义知,,
而,
显然,
于是,
两式相减得
,
因此,
当足够大时,,,则,可认为.
所以该植物寿命期望的值是10.
【点睛】方法点睛:如果数列是等差数列,是等比数列,求数列的前n项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列的公比,然后作差求解.
18.(1)散点图见解析,负
(2),
【分析】
(1)由已知条件画出散点图,根据散点图的走向判断两个变量间的关系;
(2)计算回归直线方程中的系数,然后将代入计算即可.
【详解】(1)
由题意得散点图如图所示:
由图可知与之间成负相关关系,所以是负.
(2)
因为,,
,,
所以,,
∴关于线性回归方程为,
所以当时,.
19.(1);具有很强的线性相关性
(2)分布列见解析;
【分析】
(1)根据公式求出相关系数的值,即可判断;
(2)根据题意可知可取的为,然后计算列出分布列,求出期望即可求解.
【详解】(1)由统计表数据可得:
所以
所以相关系数 ,
因此,两个变量具有很强的线性相关性.
(2)由题意知,的可能取值为
因为 ,
,
所以 的分布列为:
所以
20.(1)①;②方案二更合理,理由见解析
(2)①,两变量线性相关性很强;②负相关,理由见解析
【分析】
(1)①利用分层抽样的概念直接计算,②根据随机抽样的特性直接判断;
(2)根据相关系数的公式可得,进而可以判断相关性的强弱及相关性.
【详解】(1)①高一学生每天的检测人数为人,
②方案二更合理,因为新冠病毒奥密克戎毒株传染性更强,潜伏期更短,分散抽检可以全面检测年级中每班学生的状况,更有利于防控筛查工作;
(2)①,
,
,
,,
故,
,两变量线性相关性很强,
②由可知变量和负相关.
可能的原因:随着核酸检测工作的开展,学校相关管理协调工作效率提高,因此用时缩短.
21.(1)选择为回归方程较宜
(2)(ⅰ)证明见解析;(ⅱ)
【分析】(1)根据表格提供数据画出散点图,并由此选择.
(2)(ⅰ)利用换元法,结合对数运算证得结论成立;(ⅱ)根据回归方程的求法求得正确答案.
【详解】(1)作出散点图如图所示.
由散点图看出样本点分布在一条指数型曲线的周围,
故选择为回归方程较宜.
(2)(i)由已知:令,则,
则,,即.所以繁殖个数的对数关于天数具有线性关系.
(ii)由(i)知繁殖个数的对数关于天数可以用线性回归方程来拟合.由表中数据可得,
,
,
得到关于的线性回归方程为,又,
因此细菌的繁殖个数关于天数的非线性回归方程为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有以下几组的统计数据:要使剩下的数据具有较强的相关关系,应去掉的一组数据是( )
A. B. C. D.
2.在一元线性回归模型中,设变量和变量的样本相关系数为,决定系数为,变量和变量的样本相关系数为,决定系数为,且,,则( )
A.和之间呈正线性相关关系,且
B.和之间呈负线性相关关系,且
C.和之间呈负线性相关关系,且
D.和之间呈正线性相关关系,且
3.已知变量和满足关系,变量y与正相关,则( )
A.与负相关,与负相关 B.与正相关,与正相关
C.与正相关,与负相关 D.与负相关,与正相关
4.已知关于变量有相关关系,由观测数据得到的样本数据散点图如图所示,则该组观测数据中关于的回归方程可能是( )
A. B.
C. D.
5.对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较,下列结论正确的是( )
A. B.
C. D.
6.对四组数据进行统计,获得如下散点图,关于其相关系数的比较,说法正确的是( )
A. B.
C. D.
7.2003年春季,我国部分地区SARS流行,党和政府采取果断措施,防治结合,很快使病情得到控制,下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据,以及根据这些数据绘制出的散点图
日期 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10 5.11 5.12
人数 100 109 115 118 121 134 141 152 168 175 186 203
下列说法:①根据此散点图,可以判断日期与人数具有线性相关关系;②根据此散点图,可以判断日期与人数具有一次函数关系.其中正确的个数为( )
A.0个 B.1个 C.2个 D.以上都不对
8.相关变量x,y的散点图如图所示,现对这两个变量进行线性相关分析.方案一:根据图中所有数据,得到回归直线方程,相关系数为;方案二:剔除点,根据剩下的数据得到回归直线方程,相关系数为.则( )
A. B.
C. D.
二、多选题
9.下列命题正确的是( )
A.已知,若,则
B.若散点图的散点均落在一条斜率非0的直线上,则决定系数
C.数据的均值为4,标准差为1,则这组数据中没有大于5的数
D.数据的75百分位数为47
10.某市7天国庆节假期期间的楼房日认购量(单位:套)与日成交量(单位:套)的折线图如下图所示,小明同学根据折线图对这7天的日认购量与日成交量作出如下判断,则下列结论正确的是( )
A.日认购量与日期正相关
B.日成交量的中位数是26
C.日成交量超过日平均成交量的有2天
D.10月7日日认购量的增量大于10月7日日成交量的增量
11.对于下列概率统计相关知识,说法正确的是( )
A.数据1,2,3,4,5,6,8,9,11的第75百分位数是7
B.若事件M,N的概率满足,且M,N相互独立,则
C.由两个分类变量,的成对样本数据计算得到,依据的独立性检验,可判断,独立
D.若一组样本数据的对应样本点都在直线上,则这组样本数据的相关系数为
12.(多选)某中学的兴趣小组在某座山测得海拔高度、气压和沸点的六组数据绘制成散点图如图所示,则下列说法正确的是( )
A.沸点与海拔高度呈正相关
B.沸点与气压呈正相关
C.沸点与海拔高度呈负相关
D.气压与海拔高度呈负相关
三、填空题
13.垃圾分类是保护环境,改善人居环境、促进城市精细化管理、保障可持续发展的重要举措.某小区为了倡导居民对生活垃圾进行分类,对垃圾分类后处理垃圾(千克)所需的费用(角)的情况作了调研,并统计得到表中几组对应数据,同时用最小二乘法得到关于的线性回归方程为,则下列正确说法的序号是 .
2 3 4 5
2 2.3 3.4
①变量之间呈正相关关系;
②可以预测当时,的值为6.88;
③表中的值为3.9;
④样本中心点为.
14.在线性回归分析中,常用作为衡量模拟效果的一个指标.
下面关于的说法:①越大,说明模型拟合的效果越好;
②越接近1,说明回归的效果越好;
③越接近1,说明回归的效果越差.请你写出所有正确说法的序号 .
15.观察下列散点图,具有相关关系的是 (填序号).
16.对变量x、y有观测数据(i=1,2,…,10),得散点图如图1所示;对变量u、v有观测数据(i=1,2,…,10),得散点图如图2所示.由这两个散点图函可以判断变量x与y ,u与v .(填写“正相关”或“负相关”)
四、解答题
17.将保护区分为面积大小相近的多个区域,用简单随机抽样的方法抽取其中15个区域进行编号,统计抽取到每个区域的某种水源指标和区域内该植物分布的数量(,2,…,15),得到数组.已知,,.
(1)求样本(,2…,15)的相关系数;
(2)假设该植物的寿命为随机变量X(X可取任意正整数).研究人员统计大量数据后发现:对于任意的,寿命为的样本在寿命超过k的样本里的数量占比与寿命为1的样本在全体样本中的数量占比相同,均等于0.1,这种现象被称为“几何分布的无记忆性”.
(ⅰ)求()的表达式;
(ⅱ)推导该植物寿命期望的值.
附:相关系数.
18.某校数学建模学生社团进行了一项实验研究,采集了的一组数据如下表所示:
2 3 4 5 6 7
52.5 45 40 30 25 17.5
该社团对上述数据进行了分析,发现与之间具有线性相关关系.
(1)画出表中数据的散点图,并指出与之间的相关系数是正还是负;
(2)求出关于的线性回归方程,并写出当时,预测数据的值.
附:在线性回归方程中,,其中为样本平均值.
19.党的二十大以来,国家不断加大对科技创新的支持力度,极大鼓舞了企业持续投入研发的信心.某科技企业在国家一系列优惠政策的大力扶持下,通过不断的研发和技术革新,提升了企业收益水平.下表是对2023 年1 ~5月份该企业的利润y(单位:百万)的统计.
月份 1 月 2 月 3 月 4 月 5 月
月份编号x 1 2 3 4 5
利润y(百万) 7 12 13 19 24
(1)根据统计表,求该企业的利润y与月份编号x的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(,则认为y与x的线性相关性较强,,则认为y与x的线性相关性较弱.);
(2)该企业现有甲、乙两条流水线生产同一种产品.为对产品质量进行监控,质检人员先用简单随机抽样的方法从甲、乙两条流水线上分别抽取了5件、3件产品进行初检,再从中随机选取3件做进一步的质检,记抽到“甲流水线产品”的件数为,试求的分布列与期望.
附:相关系数
20.新冠病毒奥密克戎毒株开始流行后,为了控制新冠肺炎疫情,杭州某高中开展了每周核酸检测工作.周一至周五,每天中午13:30开始,安排位师生进行核酸检测,教职工每天都要检测,用五天时间实现全员覆盖.
(1)该校教职工有人,高二学生有人,高三学生有人.
①用分层抽样的方法,求高一学生每天的检测人数.
②高一年级共个班,该年级每天进行核酸检测的学生有两种安排方案.方案一:集中来自部分班级;方案二:分散来自所有班级.你认为哪种方案更合理?给出理由.
(2)学校开展核酸检测的第一周,周一至周五核酸检测用时记录如下表.
第天
用时
①计算变量和的相关系数(精确到),并说明两变量的线性相关程度;
②根据①中的计算结果,判定变量和是正相关还是负相关,并给出可能的原因.
参考数据和公式:,相关系数.
21.为了研究某种细菌随天数变化的繁殖个数,收集数据如下:
天数 1 2 3 4 5 6
繁殖个数 6 12 25 49 95 190
(1)在图中作出繁殖个数关于天数变化的散点图,并由散点图判断(为常数)与(为常数,且)哪一个适宜作为繁殖个数关于天数变化的回归方程类型?(给出判断即可,不必说明理由)
(2)对于非线性回归方程(为常数,且),令,可以得到繁殖个数的对数z关于天数x具有线性关系及一些统计量的值.
3.50 62.83 3.53 17.50 596.57 12.09
(ⅰ)证明:“对于非线性回归方程,令,可以得到繁殖个数的对数关于天数具有线性关系(即为常数)”;
(ⅱ)根据(ⅰ)的判断结果及表中数据,建立关于的回归方程(系数保留2位小数).
附:对于一组数据,其回归直线方程的斜率和截距的最小二乘估计分别为.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】在坐标系中画出五个点,结果除去之外,其余的点都在一条线附近,去掉这个点以后剩下的数据更具有相关关系.
【详解】,在坐标系中画出五个点,
结果除去之外,其余的点都在一条线附近,
去掉这个点以后剩下的数据更具有相关关系,
故选:C
2.A
【分析】根据相关系数的正负判断正负相关关系,根据相关系数绝对值的大小判断决定系数的大小.
【详解】因为,,故和之间呈正线性相关关系,和之间呈负线性相关关系,
故BD错误,
而,故,故A正确,C错误,
故选:A.
3.A
【分析】
根据关系式判断负相关,再由变量y与正相关可得负相关即可判断.
【详解】因为变量和满足关系,变量y与正相关,
由正相关、负相关的定义可知与负相关,与负相关.
故选:A
4.D
【分析】根据数据散点图的单调性,结合选项中的函数,逐项判定,即可求解.
【详解】由散点图可知,所求回归方程先减后增,选项中A,B均为定义域上的增函数,不符合题意;
选项C中的函数图象为开口向下的抛物线,不符合题意;
而选项D中的函数图象增减性与散点图符合题意,故D正确.
故选:D.
5.B
【分析】根据散点图分析出样本的相关关系即可.
【详解】由给出的四组数据的散点图可以看出,
左侧两图是正相关,样本相关系数大于0,则,,
右侧两图是负相关,样本相关系数小于0,则,,
下方两图的点相对更加集中,所以相关性较强,所以接近于1,接近于-1,
上方两图的点相对分散一些,所以相关性较弱,所以和比较接近0,
由此可得.
故选:B.
6.B
【分析】
根据散点图的分布判断相关系数的符号和绝对值大小,即可得结果.
【详解】由图中散点的分布趋势知:,,
由图散点的分布状态知:,,
所以.
故选:B
7.B
【分析】
作出散点图即可得出结论.
【详解】由题意,
做出散点图如下图所示,
由图可知,
日期与人数具有线性相关关系,但不是一次函数关系,
①正确,②错误,
故选:B.
8.D
【分析】根据相关系数的意义:其绝对值越接近1,说明两个变量越具有线性相关,以及负相关的意义作判断即可.
【详解】由散点图可知这两个变量为负相关,所以.
因为剔除点后,剩下点的数据更具有线性相关性,更接近1,
所以 .
故选:D.
9.ABD
【分析】对于A:利用正态分布的对称性判断;对于B:根据相关的概念判断;对于C:举反例说明;对于D:直接求75百分位数.
【详解】对于A:已知,若,
则,A正确;
对于B:若散点图的散点均落在一条斜率非0的直线上,则变量与变量之间满足线性函数关系,则决定系数,B正确;
对于C:不妨设,
则,解得,
此时,
故找到一组数,数据中有大于5的数,C错误;
对于D:,故这组数据的75百分位数为47,D正确.
故选:ABD.
10.BD
【分析】
根据正相关的定义结合图象即可判断A;根据中位数的定义结合图象即可判断B;根据图中数据进行计算即可求得平均数,即可判断C;根据图中数据进行计算即可判断D.
【详解】由题图可以看出,数据点并不是从左下至右上分布,所以错;
将成交量数据按大小顺序排列,中位数为26,所以对;
日平均成交量为,
超过42.7的只有一天,所以错;
10月7日认购量的增量为,
成交量的增量为,所以对,
故选:BD.
11.BCD
【分析】根据百分位数的定义求出第75百分位数,从而判定A;由独立性得到,进而利用对立事件的概率关系判定B;根据,可判定C;根据直线方程斜率为负值,可知相关系数为负值,根据所有点都在直线上,可知相关系数绝对值为1,进而可知相关系数,从而判定D.
【详解】对于选项A,9个数据从小到大排列,由于,所以第75百分位数应该是第7个数8,故A错误;
对于选项B,由M,N相互独立得:,所以,,故B正确:
对于选项C,由,可以认为和独立,故C正确:
对于选项D,样本点都在直线,说明是负相关且为线性函数关系,所以相关系数为,故D正确,
故选:BCD.
12.BCD
【分析】
根据散点图的特点及正相关负相关的定义即可求解.
【详解】
由左图知气压随海拔高度的增加而减小,由右图知沸点随气压的升高而升高,
所以气压与海拔高度呈负相关,沸点与气压呈正相关,沸点与海拔高度呈负相关.
故选:BCD.
13.①②④
【分析】由,可得判定①正确;令时,求得,可判定②正确;根据回归直线方程的含义与性质,可判定③错误,④正确.
【详解】对于①中,由关于的线性回归方程为,可得,
所以变量之间呈正相关关系,所以①正确;
对于②中,由关于的线性回归方程为,
当时,可得,所以②正确;
对于③中,由表格中的数据,可得,,
可得,解得,所以③错误;
对于④中,由,,即样本中心点为,所以④正确.
故答案为:①②④.
14.①②
【分析】由线性回归中的意义即可得解.
【详解】在表达式中,与经验回归方程无关,残差平方后与经验回归方程有关,因此越大,表示残差平方后越小,即模型的拟合效果越好;越小,表示残差平方和越大,即模型的拟合效果越差,可知①②正确③错误.
故答案为:①②
15.②③
【分析】根据散点图中散点的分别规律,结合相关关系的定义,逐项判定,即可求解.
【详解】散点图①中,所以的散点都在曲线上,所以①具有函数关系,不符合题意;
散点图②中,所有的散点分布在一条直线的附近,所以②具有相关关系,符合题意;
散点图③中,所有散点都分布在一条曲线的附近,所以③具有相关关系,符合题意;
散点图④中,所有的散点杂乱无章,没有分布在一条曲线的附近,所以④不具有相关关系,不符合题意.
故答案为:②③
16. 负相关 正相关
【分析】根据散点图及正相关,负相关的概念即得.
【详解】由图1可知点散布在从左上角到右下角的区域,所以变量x与y负相关,
由图2可知点散布在从左下角到右上角的区域,所以变量u与v正相关.
故答案为:负相关;正相关.
17.(1)0.8;
(2)(ⅰ);(ⅱ)10.
【分析】(1)利用给定数据及相关系数公式计算即得.
(2)先根据递推关系得到与的关系,进而利用等比数列得到通项公式,推导出的表达式,最后得到的表达式,应用错位相减法求和即可.
【详解】(1)由,,,
得相关系数.
(2)(ⅰ)依题意,,又,
则,当时,把换成,则,
两式相减,得,即,
又,于是对任意都成立,
从而是首项为0.1,公比为0.9的等比数列,
所以;
(ⅱ)由定义知,,
而,
显然,
于是,
两式相减得
,
因此,
当足够大时,,,则,可认为.
所以该植物寿命期望的值是10.
【点睛】方法点睛:如果数列是等差数列,是等比数列,求数列的前n项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列的公比,然后作差求解.
18.(1)散点图见解析,负
(2),
【分析】
(1)由已知条件画出散点图,根据散点图的走向判断两个变量间的关系;
(2)计算回归直线方程中的系数,然后将代入计算即可.
【详解】(1)
由题意得散点图如图所示:
由图可知与之间成负相关关系,所以是负.
(2)
因为,,
,,
所以,,
∴关于线性回归方程为,
所以当时,.
19.(1);具有很强的线性相关性
(2)分布列见解析;
【分析】
(1)根据公式求出相关系数的值,即可判断;
(2)根据题意可知可取的为,然后计算列出分布列,求出期望即可求解.
【详解】(1)由统计表数据可得:
所以
所以相关系数 ,
因此,两个变量具有很强的线性相关性.
(2)由题意知,的可能取值为
因为 ,
,
所以 的分布列为:
所以
20.(1)①;②方案二更合理,理由见解析
(2)①,两变量线性相关性很强;②负相关,理由见解析
【分析】
(1)①利用分层抽样的概念直接计算,②根据随机抽样的特性直接判断;
(2)根据相关系数的公式可得,进而可以判断相关性的强弱及相关性.
【详解】(1)①高一学生每天的检测人数为人,
②方案二更合理,因为新冠病毒奥密克戎毒株传染性更强,潜伏期更短,分散抽检可以全面检测年级中每班学生的状况,更有利于防控筛查工作;
(2)①,
,
,
,,
故,
,两变量线性相关性很强,
②由可知变量和负相关.
可能的原因:随着核酸检测工作的开展,学校相关管理协调工作效率提高,因此用时缩短.
21.(1)选择为回归方程较宜
(2)(ⅰ)证明见解析;(ⅱ)
【分析】(1)根据表格提供数据画出散点图,并由此选择.
(2)(ⅰ)利用换元法,结合对数运算证得结论成立;(ⅱ)根据回归方程的求法求得正确答案.
【详解】(1)作出散点图如图所示.
由散点图看出样本点分布在一条指数型曲线的周围,
故选择为回归方程较宜.
(2)(i)由已知:令,则,
则,,即.所以繁殖个数的对数关于天数具有线性关系.
(ii)由(i)知繁殖个数的对数关于天数可以用线性回归方程来拟合.由表中数据可得,
,
,
得到关于的线性回归方程为,又,
因此细菌的繁殖个数关于天数的非线性回归方程为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
