8.2一元线形回归分析 同步练习(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册
文档属性
| 名称 | 8.2一元线形回归分析 同步练习(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册 | 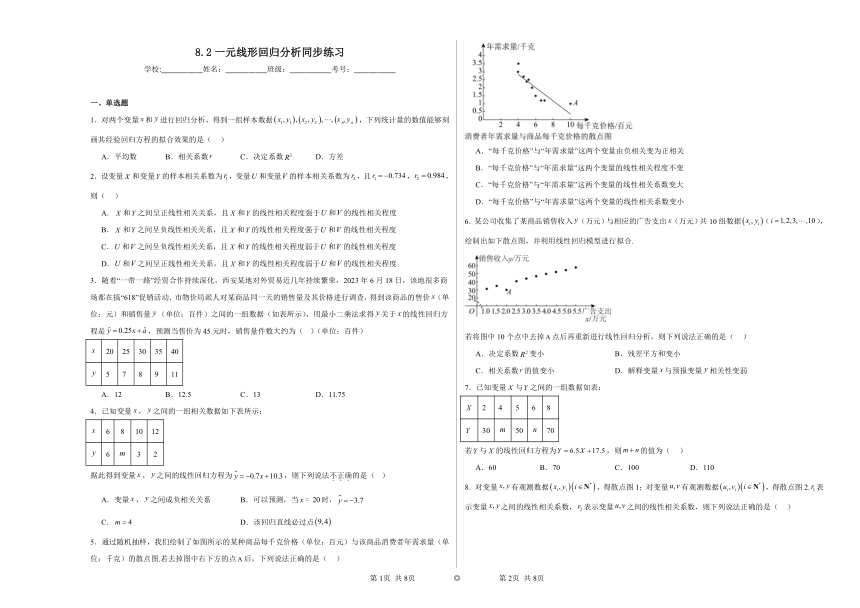 | |
| 格式 | docx | ||
| 文件大小 | 729.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-13 22:28:49 | ||
图片预览





文档简介
8.2一元线形回归分析同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.对两个变量和进行回归分析,得到一组样本数据,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )
A.平均数 B.相关系数 C.决定系数 D.方差
2.设变量和变量的样本相关系数为,变量和变量的样本相关系数为,且,,则( )
A.和之间呈正线性相关关系,且和的线性相关程度强于和的线性相关程度
B.和之间呈负线性相关关系,且和的线性相关程度强于和的线性相关程度
C.和之间呈负线性相关关系,且和的线性相关程度弱于和的线性相关程度
D.和之间呈正线性相关关系,且和的线性相关程度弱于和的线性相关程度
3.随着“一带一路”经贸合作持续深化,西安某地对外贸易近几年持续繁荣,2023年6月18日,该地很多商场都在搞“618”促销活动.市物价局派人对某商品同一天的销售量及其价格进行调查,得到该商品的售价(单位:元)和销售量(单位:百件)之间的一组数据(如表所示),用最小二乘法求得关于的线性回归方程是,预测当售价为45元时,销售量件数大约为( )(单位:百件)
20 25 30 35 40
5 7 8 9 11
A.12 B.12.5 C.13 D.11.75
4.已知变量,之间的一组相关数据如下表所示:
6 8 10 12
6 3 2
据此得到变量,之间的线性回归方程为,则下列说法不正确的是( )
A.变量,之间成负相关关系 B.可以预测,当时,
C. D.该回归直线必过点
5.通过随机抽样,我们绘制了如图所示的某种商品每千克价格(单位:百元)与该商品消费者年需求量(单位:千克)的散点图.若去掉图中右下方的点后,下列说法正确的是( )
A.“每千克价格”与“年需求量”这两个变量由负相关变为正相关
B.“每千克价格”与“年需求量”这两个变量的线性相关程度不变
C.“每千克价格”与“年需求量”这两个变量的线性相关系数变大
D.“每千克价格”与“年需求量”这两个变量的线性相关系数变小
6.某公司收集了某商品销售收入(万元)与相应的广告支出(万元)共10组数据(),绘制出如下散点图,并利用线性回归模型进行拟合.
若将图中10个点中去掉点后再重新进行线性回归分析,则下列说法正确的是( )
A.决定系数变小 B.残差平方和变小
C.相关系数的值变小 D.解释变量与预报变量相关性变弱
7.已知变量与之间的一组数据如表:
2 4 5 6 8
30 50 70
若与的线性回归方程为,则的值为( )
A.60 B.70 C.100 D.110
8.对变量有观测数据,得散点图1;对变量有观测数据,得散点图2.表示变量之间的线性相关系数,表示变量之间的线性相关系数,则下列说法正确的是( )
A.变量与呈现正相关,且 B.变量与呈现负相关,且
C.变量与呈现正相关,且 D.变量与呈现负相关,且
二、多选题
9.已知由样本数据(i=1,2,3,…,10)组成的一个样本,得到回归直线方程为,且.剔除一个偏离直线较大的异常点后,得到新的回归直线经过点.则下列说法正确的是
A.相关变量x,y具有正相关关系
B.剔除该异常点后,样本相关系数的绝对值变大
C.剔除该异常点后的回归直线方程经过点
D.剔除该异常点后,随x值增加相关变量y值减小速度变小
10.已知某产品的销售额(单位:万元)与广告费用(单位:万元)之间的关系如下表
0 1 2 3 4
10 20 30 35
若根据表中的数据用最小二乘法求得对的线性回归方程为,则下列说法中正确的是( )
A.产品的销售额与广告费用负相关
B.该回归直线过点
C.当广告费用为10万元时,销售额一定为74万元
D.的值是15
11.下列选项错误的有( )
A.若样本数据的方差为2,则数据的方差为6
B.在做回归分析时,残差图中残差比较均匀分布在以取值为0的横轴为对称轴的水平带状区域内,且宽度越窄表示回归效果越差
C.决定系数,说明回归模型较好的刻画了两个变量间的相关关系,而且响应变量可以解释97.62%的解释变量的变化
D.经验回归方程经过成对样本数据的样本中心点
12.(多选)某城市收集并整理了该市2018年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论错误的是( )
A.最低气温与最高气温呈正相关
B.10月的最高气温低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于0 ℃的月份有4个
三、填空题
13.已知某冶炼厂2023年月份煅烧的合金量(单位:百万吨)如表所示:
月份 1 2 3 4
煅烧百万吨 8.5 8 7 6.5
已知煅烧量与月份之间有较强的线性相关关系,且其线性回归方程为,则 .
14.某同学收集了变量,的相关数据如下:
x 0.5 2 3 3.5 4 5
y 15
为了研究,的相关关系,他由最小二乘法求得关于的线性回归方程为,经验证回归直线正好经过样本点,则 .
15.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元)
销量(件)
由表中数据,求得线性回归方程,若在这些样本点中任取一点,则它在回归直线右上方的概率为
16.某地建立了农业科技图书馆,供农民免费借阅,收集了近5年的借阅数据如下表:
年份 2019 2020 2021 2022 2023
年份代码 1 2 3 4 5
年借阅量万册 4.9 5.1 5.5 5.7 5.8
根据上表,可得关于的线性回归方程为.则 .
四、解答题
17.某市政府为调查集贸蔬菜市场个体承包摊户年收入情况,随机抽取了6个摊户进行分析,得到样本数据,其中和分别表示第个摊户和该摊户年收入(单位:万元),如下
1 2 3 4 5 6
5 6 7 7 9 8
(1)求关于的线性回归方程;
(2)若该集贸蔬菜市场个体承包摊户有300个,根据题设估计该集贸蔬菜市场个体承包摊户年收入总值.
参考公式:对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为.
18.20世纪80年代初,随着我国的改革开放,经济体制和经营体制逐渐灵活,市场上的商品日益丰富,城市和农村出现小卖部.小卖部主营生活日用商品,有着经营成本小、规模小、商品种类少分布广等特点.近几年,人们的生活水平达到了新的高度,实体小卖部逐渐被应运而生的大小超市所取代.为适应市场,某小卖部经营者欲将经营规模扩大,将小卖部发展成生鲜综合超市,现将2013~2022年的年利润(单位:万元)统计如下:
年限 1 2 3 4 5 6 7 8 9 10
年利润(万元) 2 8 9 12 10 13 15 16 17 18
其中,年限1表示2013年,2表示2014年,3表示2015年,……,以此类推,10表示2022年.
(1)若年利润(单位:万元)与小卖部营业年限成正相关关系,在不改变经营状态的情况下,预测该小卖部2023年的年利润;
(2)以年利润是否低于12万元为评价标准,按照分层抽样从2013~2022年的年利润中随机抽取5个,再从这5个数据中随机抽取2个,求抽取的2个数据至少有1个低于12万元的概率.
附:线性回归方程中,,其中为样本均值.
19.某农业大学组织部分学生进行作物栽培试验,由于土壤相对贫瘠,前期作物生长较为缓慢,为了增加作物的生长速度,达到预期标准,小明对自己培育的一株作物使用了营养液,现统计了使用营养液十天之内该作物的高度变化
天数x 1 2 3 4 5 6 7 8 9 10
作物高度y/cm 9 10 10 11 12 13 13 14 14 14
(1)观察散点图可知,天数与作物高度之间具有较强的线性相关性,用最小二乘法求出作物高度关于天数的线性回归方程(其中用分数表示);
(2)小明测得使用营养液后第22天该作物的高度为,请根据(1)中的结果预测第22天该作物的高度的残差.
参考公式:.参考数据:.
20.近年来,随着国家对新能源汽车产业的支持,很多国产新能源汽车迅速崛起,其因颜值高、动力充沛、提速快、空间大、用车成本低等特点得到民众的追捧,但是充电难成为影响新能源汽车销量的主要原因,国家为了加快新能源汽车的普及程度,在全国范围内逐步增建充电桩.某地区2019-2023年的充电桩数量及新能源汽车的年销量如表所示:
年份 2019 2020 2021 2022 2023
充电桩数量x/万台 1 3 5 7 9
新能源汽车年销量y/万辆 25 37 48 58 72
(1)已知可用线性回归模型拟合y与x的关系,请用相关系数加以说明(结果精确到0.001);
(2)求y关于x的线性回归方程,预测当该地区充电桩数量为24万台时,新能源汽车的年销量是多少万辆?
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,,,.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】根据相关数据的特征可知,决定系数能够刻画其经验回归方程的拟合效果.
【详解】平均数与方差是用来反馈数据集中趋势与波动程度大小的统计量;
变量y和x之间的相关系数的绝对值越大,则变量y和x之间线性相关关系越强;
用决定系数来刻画回归效果,越大说明拟合效果越好.
故选:C
2.D
【分析】根据对变量间的相关系数的意义和辨析即可得出结果.
【详解】由线性相关系数,可知变量与之间呈负线性相关关系,
由线性相关系数,可知变量与之间呈正线性相关关系,
又,
所以变量与的线性相关程度比变量与的线性相关程度强.
故选:D.
3.D
【分析】求出,,根据回归直线方程必过样本中心点求出,从而得到回归直线方程,再代入计算可得.
【详解】因为,,
所以回归直线过点,故,即,所以.
将代入中,得.
故选:D.
4.C
【分析】由,可判断A正确;当时,得到的预测值,可得判定B正确;由表格中的数据,求得样本中心,代入求得的值,可判定C不正确;由,求得,可判定D正确.
【详解】对于A中,由,可得变量之间呈现负相关关系,所以A正确;
对于B中,当,可得,所以B正确;
对于C中,由表格中的数据,可得,
则,解得,所以C不正确;
对于D中,由,可得,所以该回归直线必经过点,所以D正确.
故选:C.
5.D
【分析】根据相关系数的概念逐一判断.
【详解】对于A:去掉图中右下方的点后,根据图象,两个变量还是负相关,A错误;
对于BCD:去掉图中右下方的点后,相对来说数据会集中,相关程度会更高,
但因为是负相关,相关系数会更接近线性相关系数会变小,故D正确,BC错误.
故选:D.
6.B
【分析】从图中分析得到去掉点后,回归效果更好,再由决定系数,残差平方和,相关系数和相关性的概念和性质作出判断.
【详解】从图中可以看出点较其他点,偏离直线远,故去掉点后,回归效果更好,
故决定系数会变大,更接近于1,残差平方和变小,
相关系数的绝对值,即会更接近于1,由图可得与正相关,故会更接近于1,
即相关系数的值变大,解释变量与预报变量相关性变强,
故A、C、D错误,B正确.
故选:B.
7.C
【分析】首先求出,根据回归直线方程必过样本中心点,即可求出,再由平均数公式计算可得.
【详解】因为,又与的线性回归方程为,
所以,即,解得.
故选:C.
8.C
【分析】利用散点图,结合相关系数的知识可得答案.
【详解】由题意可知,变量的散点图中,随的增大而增大,所以变量与呈现正相关;
再分别观察两个散点图,图比图点更加集中,相关性更好,所以线性相关系数.
故选:C.
9.BC
【分析】根据给定条件,求出新样本的中心点,进而求出新回归直线的斜率,再逐项判断即得.
【详解】依题意,原样本中,,
剔除一个偏离直线较大的异常点后,新样本中,,
因此剔除该异常点后的回归直线方程经过点,C正确;
由新的回归直线经过点,得新的回归直线斜率为,因此相关变量x,y具有负相关关系,A错误;
又,则剔除该异常点后,随x值增加相关变量y值减小速度变大,D错误;
由剔除的是偏离直线较大的异常点,得剔除该点后,新样本数据的线性相关程度变强,即样本相关系数的绝对值变大,B正确.
故选:BC
10.BD
【分析】对于A项,由回归方程即可之家额判断;对于B项,计算出样本中心点即可判断;对于C项,因回归方程求出的是预报值,与实际值不一定完全吻合,故可判断,对于D项,只需根据样本中心点坐标即,运用平均数公式即可求得.
【详解】对于A项,因对的线性回归方程为,其中,故产品的销售额与广告费用正相关,即A项错误;
对于B项,由表格知,代入,解得,即样本中心点坐标为,回归直线必过样本中心点,故B项正确;
对于C项,由对的线性回归方程为知,当时,代入可得,即销售额的预报值为74万元,但实际不一定是,故C项错误;
对于D项,由B项知,即,解得.故D项正确.
故选:BD.
11.AB
【分析】根据样本数据的方差公式,残差图,以及决定系数的定义,以及回归方程的相关知识点,判断选项.
【详解】A.由条件可知,数据的方差为,故A错误;
B.由残差图的描述可知,宽度越窄表示回归效果越好,故B错误;
C.决定系数反映了因变量的变异中可以被自变量解释的比例,故C正确.
D. 经验回归方程经过成对样本数据的样本中心点,故D正确.
故选:AB
12.BD
【详解】
在A中,最低气温与最高气温呈正相关,故A正确;在B中,10月的最高气温不低于5月的最高气温,故B错误;在C中,月温差(最高气温减最低气温)的最大值出现在1月,故C正确;在D中,最低气温低于0 ℃的月份有3个,故D错误.
13.9.25
【分析】根据回归直线一定过样本中心点,求出样本中心点,然后代入回归方程即可求出.
【详解】,,
.
故答案为:
14.69
【分析】结合线性回归方程必过样本中心点求解.
【详解】因为线性回归方程经过样本点,所以.
因为:,所以.
所以:.
故答案为:69
15./
【分析】根据表中数据可得回归方程,进而确定在回归直线右上方的个数,进而可得概率.
【详解】由已知,,
又样本中心在回归直线上,
即,解得,
所以回归直线方程为,
当时,,所以点在回归直线上;
当时,,所以点在回归直线左下方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线左下方;
所以个样本点中在回归直线右上方的有个,
所以在这些样本点中任取一点,则它在回归直线右上方的概率为,
故答案为:.
16.
【分析】
利用回归方程过样本中心点,代入计算即可求得
【详解】
根据表格可知,
,,
代入,可得.
故答案为:
17.(1)
(2)万元
【分析】(1)根据所给数据求出、、、,从而求出,再由即可得到结果;
(2)由条件可得,该集市摊户的年收入总值是以为首项,以为公差的等差数列的前300项和,结合等差数列的求和公式,即可得到结果.
【详解】(1)题意计算得,则,,则,
所以
则,,
所以.
(2)由题可知,第1个摊户的年收入为万元,
第2个摊户的年收入为万元,
第300个摊户的年收入为万元,
所以该集市摊户的年收入总值是以为首项,以为公差的等差数列的前300项和,
设为,则万元.
所以该集贸蔬菜市场个体承包摊户年收入总值约为万元.
18.(1)20.47万元
(2)
【分析】(1)根据图表利用最小二乘法计算线性回归方程并预测即可;
(2)根据图表利用分层抽样及古典概型计算即可.
【详解】(1),
,
,
,
线性回归方程为.
当时,,
在不改变经营状态的情况下,预测该小卖部2023年的年利润为20.47万元.
(2)2013~2022年的年利润中低于12万元的有4个,不低于12万元的有6个,
按照分层抽样从2013~2022年的年利润中随机抽取5个,
则年利润低于12万元的有2个,记为,不低于12万元的有3个,
记为.
从这5个数据中随机抽取2个,
所有等可能结果有,,共10种,
其中,抽取的2个数据至少有1个低于12万元的结果有,共7种,
故所求概率为.
19.(1);
(2).
【分析】(1)根据表格数据利用公式求出即可求解.
(2)将代入回归方程求得预测值,然后根据残差定义求解即可.
【详解】(1)依题意,,
,
故,
,故所求回归直线方程为.
(2)由(1)可知,当时,,
故所求残差为.
20.(1)答案见解析
(2);157.25万辆
【分析】(1)先求出,,结合题意中的公式计算即可求解;
(2)根据最小二乘法计算,进而求出,写出线性回归方程.将代入方程即可下结论.
【详解】(1)由题知,,
又,,,
所以,
因为y与x的相关系数近似为0.999,非常接近1,
所以y与x的线性相关程度很高,可以用线性回归模型拟合y与x的关系.
(2),,
所以y关于x的线性回归方程为.
当时,,
故当充电桩数量为24万台时,该地区新能源汽车的年销量为157.25万辆.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.对两个变量和进行回归分析,得到一组样本数据,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )
A.平均数 B.相关系数 C.决定系数 D.方差
2.设变量和变量的样本相关系数为,变量和变量的样本相关系数为,且,,则( )
A.和之间呈正线性相关关系,且和的线性相关程度强于和的线性相关程度
B.和之间呈负线性相关关系,且和的线性相关程度强于和的线性相关程度
C.和之间呈负线性相关关系,且和的线性相关程度弱于和的线性相关程度
D.和之间呈正线性相关关系,且和的线性相关程度弱于和的线性相关程度
3.随着“一带一路”经贸合作持续深化,西安某地对外贸易近几年持续繁荣,2023年6月18日,该地很多商场都在搞“618”促销活动.市物价局派人对某商品同一天的销售量及其价格进行调查,得到该商品的售价(单位:元)和销售量(单位:百件)之间的一组数据(如表所示),用最小二乘法求得关于的线性回归方程是,预测当售价为45元时,销售量件数大约为( )(单位:百件)
20 25 30 35 40
5 7 8 9 11
A.12 B.12.5 C.13 D.11.75
4.已知变量,之间的一组相关数据如下表所示:
6 8 10 12
6 3 2
据此得到变量,之间的线性回归方程为,则下列说法不正确的是( )
A.变量,之间成负相关关系 B.可以预测,当时,
C. D.该回归直线必过点
5.通过随机抽样,我们绘制了如图所示的某种商品每千克价格(单位:百元)与该商品消费者年需求量(单位:千克)的散点图.若去掉图中右下方的点后,下列说法正确的是( )
A.“每千克价格”与“年需求量”这两个变量由负相关变为正相关
B.“每千克价格”与“年需求量”这两个变量的线性相关程度不变
C.“每千克价格”与“年需求量”这两个变量的线性相关系数变大
D.“每千克价格”与“年需求量”这两个变量的线性相关系数变小
6.某公司收集了某商品销售收入(万元)与相应的广告支出(万元)共10组数据(),绘制出如下散点图,并利用线性回归模型进行拟合.
若将图中10个点中去掉点后再重新进行线性回归分析,则下列说法正确的是( )
A.决定系数变小 B.残差平方和变小
C.相关系数的值变小 D.解释变量与预报变量相关性变弱
7.已知变量与之间的一组数据如表:
2 4 5 6 8
30 50 70
若与的线性回归方程为,则的值为( )
A.60 B.70 C.100 D.110
8.对变量有观测数据,得散点图1;对变量有观测数据,得散点图2.表示变量之间的线性相关系数,表示变量之间的线性相关系数,则下列说法正确的是( )
A.变量与呈现正相关,且 B.变量与呈现负相关,且
C.变量与呈现正相关,且 D.变量与呈现负相关,且
二、多选题
9.已知由样本数据(i=1,2,3,…,10)组成的一个样本,得到回归直线方程为,且.剔除一个偏离直线较大的异常点后,得到新的回归直线经过点.则下列说法正确的是
A.相关变量x,y具有正相关关系
B.剔除该异常点后,样本相关系数的绝对值变大
C.剔除该异常点后的回归直线方程经过点
D.剔除该异常点后,随x值增加相关变量y值减小速度变小
10.已知某产品的销售额(单位:万元)与广告费用(单位:万元)之间的关系如下表
0 1 2 3 4
10 20 30 35
若根据表中的数据用最小二乘法求得对的线性回归方程为,则下列说法中正确的是( )
A.产品的销售额与广告费用负相关
B.该回归直线过点
C.当广告费用为10万元时,销售额一定为74万元
D.的值是15
11.下列选项错误的有( )
A.若样本数据的方差为2,则数据的方差为6
B.在做回归分析时,残差图中残差比较均匀分布在以取值为0的横轴为对称轴的水平带状区域内,且宽度越窄表示回归效果越差
C.决定系数,说明回归模型较好的刻画了两个变量间的相关关系,而且响应变量可以解释97.62%的解释变量的变化
D.经验回归方程经过成对样本数据的样本中心点
12.(多选)某城市收集并整理了该市2018年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论错误的是( )
A.最低气温与最高气温呈正相关
B.10月的最高气温低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于0 ℃的月份有4个
三、填空题
13.已知某冶炼厂2023年月份煅烧的合金量(单位:百万吨)如表所示:
月份 1 2 3 4
煅烧百万吨 8.5 8 7 6.5
已知煅烧量与月份之间有较强的线性相关关系,且其线性回归方程为,则 .
14.某同学收集了变量,的相关数据如下:
x 0.5 2 3 3.5 4 5
y 15
为了研究,的相关关系,他由最小二乘法求得关于的线性回归方程为,经验证回归直线正好经过样本点,则 .
15.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元)
销量(件)
由表中数据,求得线性回归方程,若在这些样本点中任取一点,则它在回归直线右上方的概率为
16.某地建立了农业科技图书馆,供农民免费借阅,收集了近5年的借阅数据如下表:
年份 2019 2020 2021 2022 2023
年份代码 1 2 3 4 5
年借阅量万册 4.9 5.1 5.5 5.7 5.8
根据上表,可得关于的线性回归方程为.则 .
四、解答题
17.某市政府为调查集贸蔬菜市场个体承包摊户年收入情况,随机抽取了6个摊户进行分析,得到样本数据,其中和分别表示第个摊户和该摊户年收入(单位:万元),如下
1 2 3 4 5 6
5 6 7 7 9 8
(1)求关于的线性回归方程;
(2)若该集贸蔬菜市场个体承包摊户有300个,根据题设估计该集贸蔬菜市场个体承包摊户年收入总值.
参考公式:对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为.
18.20世纪80年代初,随着我国的改革开放,经济体制和经营体制逐渐灵活,市场上的商品日益丰富,城市和农村出现小卖部.小卖部主营生活日用商品,有着经营成本小、规模小、商品种类少分布广等特点.近几年,人们的生活水平达到了新的高度,实体小卖部逐渐被应运而生的大小超市所取代.为适应市场,某小卖部经营者欲将经营规模扩大,将小卖部发展成生鲜综合超市,现将2013~2022年的年利润(单位:万元)统计如下:
年限 1 2 3 4 5 6 7 8 9 10
年利润(万元) 2 8 9 12 10 13 15 16 17 18
其中,年限1表示2013年,2表示2014年,3表示2015年,……,以此类推,10表示2022年.
(1)若年利润(单位:万元)与小卖部营业年限成正相关关系,在不改变经营状态的情况下,预测该小卖部2023年的年利润;
(2)以年利润是否低于12万元为评价标准,按照分层抽样从2013~2022年的年利润中随机抽取5个,再从这5个数据中随机抽取2个,求抽取的2个数据至少有1个低于12万元的概率.
附:线性回归方程中,,其中为样本均值.
19.某农业大学组织部分学生进行作物栽培试验,由于土壤相对贫瘠,前期作物生长较为缓慢,为了增加作物的生长速度,达到预期标准,小明对自己培育的一株作物使用了营养液,现统计了使用营养液十天之内该作物的高度变化
天数x 1 2 3 4 5 6 7 8 9 10
作物高度y/cm 9 10 10 11 12 13 13 14 14 14
(1)观察散点图可知,天数与作物高度之间具有较强的线性相关性,用最小二乘法求出作物高度关于天数的线性回归方程(其中用分数表示);
(2)小明测得使用营养液后第22天该作物的高度为,请根据(1)中的结果预测第22天该作物的高度的残差.
参考公式:.参考数据:.
20.近年来,随着国家对新能源汽车产业的支持,很多国产新能源汽车迅速崛起,其因颜值高、动力充沛、提速快、空间大、用车成本低等特点得到民众的追捧,但是充电难成为影响新能源汽车销量的主要原因,国家为了加快新能源汽车的普及程度,在全国范围内逐步增建充电桩.某地区2019-2023年的充电桩数量及新能源汽车的年销量如表所示:
年份 2019 2020 2021 2022 2023
充电桩数量x/万台 1 3 5 7 9
新能源汽车年销量y/万辆 25 37 48 58 72
(1)已知可用线性回归模型拟合y与x的关系,请用相关系数加以说明(结果精确到0.001);
(2)求y关于x的线性回归方程,预测当该地区充电桩数量为24万台时,新能源汽车的年销量是多少万辆?
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,,,.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】根据相关数据的特征可知,决定系数能够刻画其经验回归方程的拟合效果.
【详解】平均数与方差是用来反馈数据集中趋势与波动程度大小的统计量;
变量y和x之间的相关系数的绝对值越大,则变量y和x之间线性相关关系越强;
用决定系数来刻画回归效果,越大说明拟合效果越好.
故选:C
2.D
【分析】根据对变量间的相关系数的意义和辨析即可得出结果.
【详解】由线性相关系数,可知变量与之间呈负线性相关关系,
由线性相关系数,可知变量与之间呈正线性相关关系,
又,
所以变量与的线性相关程度比变量与的线性相关程度强.
故选:D.
3.D
【分析】求出,,根据回归直线方程必过样本中心点求出,从而得到回归直线方程,再代入计算可得.
【详解】因为,,
所以回归直线过点,故,即,所以.
将代入中,得.
故选:D.
4.C
【分析】由,可判断A正确;当时,得到的预测值,可得判定B正确;由表格中的数据,求得样本中心,代入求得的值,可判定C不正确;由,求得,可判定D正确.
【详解】对于A中,由,可得变量之间呈现负相关关系,所以A正确;
对于B中,当,可得,所以B正确;
对于C中,由表格中的数据,可得,
则,解得,所以C不正确;
对于D中,由,可得,所以该回归直线必经过点,所以D正确.
故选:C.
5.D
【分析】根据相关系数的概念逐一判断.
【详解】对于A:去掉图中右下方的点后,根据图象,两个变量还是负相关,A错误;
对于BCD:去掉图中右下方的点后,相对来说数据会集中,相关程度会更高,
但因为是负相关,相关系数会更接近线性相关系数会变小,故D正确,BC错误.
故选:D.
6.B
【分析】从图中分析得到去掉点后,回归效果更好,再由决定系数,残差平方和,相关系数和相关性的概念和性质作出判断.
【详解】从图中可以看出点较其他点,偏离直线远,故去掉点后,回归效果更好,
故决定系数会变大,更接近于1,残差平方和变小,
相关系数的绝对值,即会更接近于1,由图可得与正相关,故会更接近于1,
即相关系数的值变大,解释变量与预报变量相关性变强,
故A、C、D错误,B正确.
故选:B.
7.C
【分析】首先求出,根据回归直线方程必过样本中心点,即可求出,再由平均数公式计算可得.
【详解】因为,又与的线性回归方程为,
所以,即,解得.
故选:C.
8.C
【分析】利用散点图,结合相关系数的知识可得答案.
【详解】由题意可知,变量的散点图中,随的增大而增大,所以变量与呈现正相关;
再分别观察两个散点图,图比图点更加集中,相关性更好,所以线性相关系数.
故选:C.
9.BC
【分析】根据给定条件,求出新样本的中心点,进而求出新回归直线的斜率,再逐项判断即得.
【详解】依题意,原样本中,,
剔除一个偏离直线较大的异常点后,新样本中,,
因此剔除该异常点后的回归直线方程经过点,C正确;
由新的回归直线经过点,得新的回归直线斜率为,因此相关变量x,y具有负相关关系,A错误;
又,则剔除该异常点后,随x值增加相关变量y值减小速度变大,D错误;
由剔除的是偏离直线较大的异常点,得剔除该点后,新样本数据的线性相关程度变强,即样本相关系数的绝对值变大,B正确.
故选:BC
10.BD
【分析】对于A项,由回归方程即可之家额判断;对于B项,计算出样本中心点即可判断;对于C项,因回归方程求出的是预报值,与实际值不一定完全吻合,故可判断,对于D项,只需根据样本中心点坐标即,运用平均数公式即可求得.
【详解】对于A项,因对的线性回归方程为,其中,故产品的销售额与广告费用正相关,即A项错误;
对于B项,由表格知,代入,解得,即样本中心点坐标为,回归直线必过样本中心点,故B项正确;
对于C项,由对的线性回归方程为知,当时,代入可得,即销售额的预报值为74万元,但实际不一定是,故C项错误;
对于D项,由B项知,即,解得.故D项正确.
故选:BD.
11.AB
【分析】根据样本数据的方差公式,残差图,以及决定系数的定义,以及回归方程的相关知识点,判断选项.
【详解】A.由条件可知,数据的方差为,故A错误;
B.由残差图的描述可知,宽度越窄表示回归效果越好,故B错误;
C.决定系数反映了因变量的变异中可以被自变量解释的比例,故C正确.
D. 经验回归方程经过成对样本数据的样本中心点,故D正确.
故选:AB
12.BD
【详解】
在A中,最低气温与最高气温呈正相关,故A正确;在B中,10月的最高气温不低于5月的最高气温,故B错误;在C中,月温差(最高气温减最低气温)的最大值出现在1月,故C正确;在D中,最低气温低于0 ℃的月份有3个,故D错误.
13.9.25
【分析】根据回归直线一定过样本中心点,求出样本中心点,然后代入回归方程即可求出.
【详解】,,
.
故答案为:
14.69
【分析】结合线性回归方程必过样本中心点求解.
【详解】因为线性回归方程经过样本点,所以.
因为:,所以.
所以:.
故答案为:69
15./
【分析】根据表中数据可得回归方程,进而确定在回归直线右上方的个数,进而可得概率.
【详解】由已知,,
又样本中心在回归直线上,
即,解得,
所以回归直线方程为,
当时,,所以点在回归直线上;
当时,,所以点在回归直线左下方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线右上方;
当时,,所以点在回归直线左下方;
所以个样本点中在回归直线右上方的有个,
所以在这些样本点中任取一点,则它在回归直线右上方的概率为,
故答案为:.
16.
【分析】
利用回归方程过样本中心点,代入计算即可求得
【详解】
根据表格可知,
,,
代入,可得.
故答案为:
17.(1)
(2)万元
【分析】(1)根据所给数据求出、、、,从而求出,再由即可得到结果;
(2)由条件可得,该集市摊户的年收入总值是以为首项,以为公差的等差数列的前300项和,结合等差数列的求和公式,即可得到结果.
【详解】(1)题意计算得,则,,则,
所以
则,,
所以.
(2)由题可知,第1个摊户的年收入为万元,
第2个摊户的年收入为万元,
第300个摊户的年收入为万元,
所以该集市摊户的年收入总值是以为首项,以为公差的等差数列的前300项和,
设为,则万元.
所以该集贸蔬菜市场个体承包摊户年收入总值约为万元.
18.(1)20.47万元
(2)
【分析】(1)根据图表利用最小二乘法计算线性回归方程并预测即可;
(2)根据图表利用分层抽样及古典概型计算即可.
【详解】(1),
,
,
,
线性回归方程为.
当时,,
在不改变经营状态的情况下,预测该小卖部2023年的年利润为20.47万元.
(2)2013~2022年的年利润中低于12万元的有4个,不低于12万元的有6个,
按照分层抽样从2013~2022年的年利润中随机抽取5个,
则年利润低于12万元的有2个,记为,不低于12万元的有3个,
记为.
从这5个数据中随机抽取2个,
所有等可能结果有,,共10种,
其中,抽取的2个数据至少有1个低于12万元的结果有,共7种,
故所求概率为.
19.(1);
(2).
【分析】(1)根据表格数据利用公式求出即可求解.
(2)将代入回归方程求得预测值,然后根据残差定义求解即可.
【详解】(1)依题意,,
,
故,
,故所求回归直线方程为.
(2)由(1)可知,当时,,
故所求残差为.
20.(1)答案见解析
(2);157.25万辆
【分析】(1)先求出,,结合题意中的公式计算即可求解;
(2)根据最小二乘法计算,进而求出,写出线性回归方程.将代入方程即可下结论.
【详解】(1)由题知,,
又,,,
所以,
因为y与x的相关系数近似为0.999,非常接近1,
所以y与x的线性相关程度很高,可以用线性回归模型拟合y与x的关系.
(2),,
所以y关于x的线性回归方程为.
当时,,
故当充电桩数量为24万台时,该地区新能源汽车的年销量为157.25万辆.
答案第1页,共2页
答案第1页,共2页
同课章节目录
