第8章 成对数据的统计分析 综合复习训练(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册
文档属性
| 名称 | 第8章 成对数据的统计分析 综合复习训练(含解析)2023——2024学年沪教版(2020)高中数学选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 791.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 08:43:41 | ||
图片预览




文档简介
第8章成对数据的统计分析综合复习训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.针对2025年第九届亚冬会在哈尔滨举办,校团委对“是否喜欢冰雪运动与学生性别的关系”进行了一次调查,其中被调查的男、女生人数相同,男生中喜欢冰雪运动的人数占男生人数的,女生中喜欢冰雪运动的人数占女生人数的,若依据的独立性检验,认为是否喜欢冰雪运动与学生性别有关,则被调查的学生中男生的人数不可( )
附:.
0.1 0.05 0.01 0.005 0.001
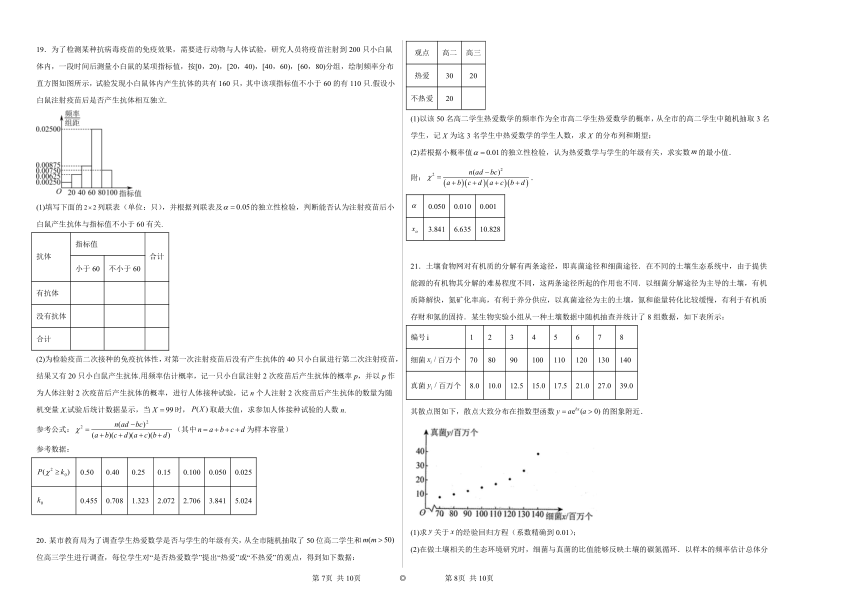
2.706 3.841 6.635 7.879 10.828
A.48 B.54 C.60 D.66
2.开始吸烟年龄与得肺癌的相对危险度相对应的一组数据为,;每天吸烟的支数与其得肺癌的相对危险度相对应的一组数据为,.用表示变量与之间的线性相关系数,用表示变量与之间的线性相关系数,则下列说法正确的是( )
A. B. C. D.
3.用最小二乘法得到一组数据的线性回归方程为,若,则等于( )
A.53 B.65 C.13 D.11
4.校数学兴趣社团对“学生性别和选学生物学是否有关”作了尝试性调查.其中被调查的男女生人数相同.男生选学生物学的人数占男生人数的,女生选学生物学的人数占女生人数.若有的把握认为选学生物学和性别有关,则调查人数中男生不可能有( )人.
附表:
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
其中,.
A.20 B.30 C.35 D.40
5.某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到两种疗法治疗数据的列联表:
疗法 疗效 合计
未治愈 治愈
甲 15 52 67
乙 6 63 69
合计 21 115 136
经计算得到,根据小概率值的独立性检验(已知独立性检验中),则可以认为( )
A.两种疗法的效果存在差异
B.两种疗法的效果存在差异,这种判断犯错误的概率不超过0.005
C.两种疗法的效果没有差异
D.两种疗法的效果没有差异,这种判断犯错误的概率不超过0.005
6.下列说法错误的是( )
A.若随机变量、满足且,则
B.样本数据,,,,,,,,,的第百分位数为
C.若事件、相互独立,则
D.若、两组成对数据的相关系数分别为、,则组数据的相关性更强
7.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得数据如下表:已知该产品的色度y和色差x之间满足线性相关关系,且,现有一组测量数据为,则该数据的残差为( )
色差x 22 24 26 28
色度y 16 19 20 21
A. B. C. D.
8.某老师很喜欢某APP中的“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数,如下表:
天数 1 2 3 4 5 6 7
一次最多答对题数 14 16 18 21 21 a 27
根据最小二乘法得到关于的回归直线方程为,则( )
A.22 B.23 C.24 D.25
二、多选题
9.某厂近几年陆续购买了几台 A 型机床,该型机床已投入生产的时间x(单位:年)与当年所需要支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7
根据表中的数据可得到经验回归方程为. 则( )
A.
B.y与x的样本相关系数
C.表中维修费用的第60百分位数为6
D.该型机床已投入生产的时间为 10年时,当年所需要支出的维修费用一定是12.38万元
10.下列说法中正确的是( )
A.公式中的和不具有线性相关关系
B.已知变量的对数据为,则回归直线可以不经过点,其中
C.若相关系数的绝对值越接近1,则两个变量的线性相关性越强
D.对于变量与的统计量来说,越大,判断“与有关系”的把握越大
11.某地为响应“扶贫必扶智,扶智就是扶知识、扶技术、扶方法”的号召,建立农业科技图书馆,供农民免费借阅,收集了近5年借阅数据如下表:
年份代码x 1 2 3 4 5
年借阅量y(万册) 4.9 5.1 5.5 5.7 5.8
根据上表,可得y关于x的经验回归方程为,下列结论正确的有( )
A.
B.借阅量4.9,5.1,5.5,5.7,5.8的75%分位数为5.7
C.y与x的线性相关系数
D.第六年的借阅量一定不少于6.12万册
12.(多选)人们常将男子短跑100 m的高水平运动员称为“百米飞人”,表中给出了1968年之前部分男子短跑100 m世界纪录产生的年份和世界纪录的数据:
第x次 1 2 3 4 5
年份 1930 1936 1956 1960 1968
纪录/s 10.30 10.20 10.10 10.00 9.95
如果变量y与x之间具有线性相关关系,设用最小二乘法建立的回归直线方程为=-0.11x+,则下列说法正确的是( )
A.变量y与x之间是正相关关系
B.变量y与x之间的线性相关系数r>0
C.=10.44
D.下一次世界纪录在9.78 s左右
三、填空题
13.某同学在研究变量,之间的相关关系时,得到以下数据:并采用最小二乘法得到了线性回归方程,则 0(填“>”或“<”).
4.8 5.8 7 8.3 9.1
2.8 4.1 7.2 9.1 11.8
14.为检验某种药物预防某一疾病的效果,进行了动物试验,得到如下2×2列联表:
患病 未患病 总计
服用药 10 45 55
没服用药 20 30 50
总计 30 75 105
由上述数据给出下列结论,其中结论正确的是 .(填序号)
① 不能在犯错误的概率不超过0.05的前提下认为药物有效;
② 能在犯错误的概率不超过0.025的前提下认为药物有效;
③ 不能在犯错误的概率不超过0.010的前提下认为药物有效;
④ 能在犯错误的概率不超过0.005的前提下认为药物有效.
15.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是正相关,其相关系数 (结果保留两位小数).
16.某公司为了增加某商品的销售利润,调查了该商品投入的广告费用:(单位:万元)与销售利润(单位:万元)的相关数据,如表所示,根据表中数据,得到经验回归方程,则下列命题正确的是 (请填写序号)
广告费用 3 4 5 8
销售利润 4 5 7 8
①; ②;③直线必过点;④直线必过点
四、解答题
17.新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.某中医药企业根据市场调研与模拟,得到研发投入(亿元)与产品收益(亿元)的数据统计如下:
研发投入x(亿元) 1 2 3 4 5
产品收益y(亿元) 3 7 9 10 11
(1)计算的相关系数,并判断是否可以认为研发投入与产品收益具有较高的线性相关程度?(若,则线性相关程度一般,若,则线性相关程度较高)
(2)求出关于的线性回归方程,并预测若想收益超过50(亿元)则需研发投入至少多少亿元?(结果保留一位小数)
参考数据:;
附:相关系数公式:;
回归直线方程的斜率.
18.某校为了让学生有一个良好的学习环境,特制定学生满意度调查表,调查表分值满分为100分.工作人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如图.
(1)估计此次满意度调查所得的平均分值(同一组中的数据用该组区间的中点值为代表);
(2)在选取的100位学生中,男女生人数相同,规定分值在(1)中的以上为满意,低于为不满意,据统计有32位男生满意.据此判断是否有的把握认为“学生满意度与性别有关”?
(3)在(2)的条件下,学校从满意度分值低于分的学生中抽取部分进行座谈,先用分层抽样的方式选出8位学生,再从中随机抽取2人,求恰好抽到男女生各一人的概率.
附:,其中.
19.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验,研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[0,20),[20,40),[40,60),[60,80)分组,绘制频率分布直方图如图所示,试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表(单位:只),并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.用频率估计概率,记一只小白鼠注射2次疫苗后产生抗体的概率p,并以p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n个人注射2次疫苗后产生抗体的数量为随机变量X.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数n.
参考公式:(其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
20.某市教育局为了调查学生热爱数学是否与学生的年级有关,从全市随机抽取了50位高二学生和位高三学生进行调查,每位学生对“是否热爱数学”提出“热爱”或“不热爱”的观点,得到如下数据:
观点 高二 高三
热爱 30 20
不热爱 20
(1)以该50名高二学生热爱数学的频率作为全市高二学生热爱数学的概率,从全市的高二学生中随机抽取3名学生,记为这3名学生中热爱数学的学生人数,求的分布列和期望;
(2)若根据小概率值的独立性检验,认为热爱数学与学生的年级有关,求实数的最小值.
附:.
0.050 0.010 0.001
3.841 6.635 10.828
21.土壤食物网对有机质的分解有两条途径,即真菌途径和细菌途径.在不同的土壤生态系统中,由于提供能源的有机物其分解的难易程度不同,这两条途径所起的作用也不同.以细菌分解途径为主导的土壤,有机质降解快,氮矿化率高,有利于养分供应,以真菌途径为主的土壤,氮和能量转化比较缓慢,有利于有机质存财和氮的固持.某生物实验小组从一种土壤数据中随机抽查并统计了8组数据,如下表所示:
编号 1 2 3 4 5 6 7 8
细菌百万个 70 80 90 100 110 120 130 140
真菌百万个 8.0 10.0 12.5 15.0 17.5 21.0 27.0 39.0
其散点图如下,散点大致分布在指数型函数的图象附近.
(1)求关于的经验回归方程(系数精确到0.01);
(2)在做土壤相关的生态环境研究时,细菌与真菌的比值能够反映土壤的碳氮循环.以样本的频率估计总体分布的概率,若该实验小组随机抽查8组数据,再从中任选4组,记真菌(单位:百万个)与细菌(单位:百万个)的数值之比位于区间内的组数为,求的分布列与数学期望.
附:经验回归方程的斜率和截距的最小二乘估计公式分别为,
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】根据已知条件设男生人数为,结合独立性检验公式得出不等式,根据的取值,即可求解.
【详解】设男生人数为,因为被调查的男、女生人数相同,
所以女生人数也为,根据题意列出列联表:
男生 女生 合计
喜欢冰雪运动
不喜欢冰雪运动
合计
则,
因为依据的独立性检验,认为是否喜欢冰雪运动与学生性别有关,
所以,即,解得,又,
所以B、C、D正确,A错误.
故选:A
2.D
【分析】借助线性相关系数的定义判断即可得.
【详解】由与相对应的数据可得,随的增大而减小,呈负相关,故,
由与相对应的数据可得,随的增大而增大,呈正相关,故,
故.
故选:D.
3.B
【分析】根据题意,由条件可得,由线性回归方程必过样本中心,代入计算,即可得到结果.
【详解】因为,则,代入可得,
所以.
故选:B
4.A
【分析】借助卡方计算即可得.
【详解】设总人数为,则男生选学生物学的人数为,女生选生物学的人数为,
则,
即,又为的倍数,故男生最少有人.
故选:A.
5.C
【分析】根据条件可得列联表,计算的值,结合临界值表可得结论.
【详解】零假设为:疗法与疗效独立,即两种疗法效果没有差异.
根据列联表中的数据,,根据小概率值的独立性检验,
没有充分证据推断不成立,
因此可以认为成立,
即认为两种疗法效果没有差异.
故选:C.
6.D
【分析】根据方差的性质判断A,根据百分位数计算规则判断B,根据相互独立事件及条件概率概率公式判断C,根据相关系数的概念判断D.
【详解】对于A:因为且,所以,故A正确;
对于B:因为,所以第百分位数为从小到大排列的第个数,即为,故B正确;
对于C:若事件、相互独立,则,
所以,故C正确;
对于D:若、两组成对数据的相关系数分别为、,
因为,所以组数据的相关性更强,故D错误.
故选:D
7.D
【分析】根据题意,由回归直线方程过样本中心点,即可得到,然后代入计算,即可得到结果.
【详解】由题意可知,,,
将代入,即,解得,
所以,当时,,
所以该数据的残差为.
故选:D.
8.B
【分析】求出回归中心,代入回归方程求解即可.
【详解】因为,,所以,解得.
故选:B.
9.ABC
【分析】对A,计算出样本中心,代入方程计算出,对B,根据相关系数的概念可判断,对C,根据百分位数的定义求解,对D,根据回归分析概念判断.
【详解】根据题意可得,,,
所以样本中心点为,
对于A,将样本中心点代入回归方程,可得,故A正确;
对于B,由表中数据可得随着增大而增大,与正相关,所以相关系数,故B正确;
对于C,维修费用从小到大依次为,第60百分位数为,故C正确;
对于D,根据回归分析的概念,机床投入生产的时间为 10年时,所需要支出的维修费用大概是12.38万元,故D错误.
故选:ABC.
10.ACD
【分析】A选项,根据线性相关的定义进行判断;B选项,回归直线一定经过样本中心点;C选项,由相关系数的性质进行判断;D选项,根据的定义判断D正确.
【详解】A选,公式中的和为二次函数关系,故不具有线性相关关系,A正确;
B选项,回归直线一定经过样本中心点,即,B错误;
C选项,若相关系数的绝对值越接近1,则两个变量的线性相关性越强,C正确;
D选项,对于变量与的统计量来说,越大,判断“与有关系”的把握越大,D正确.
故选:ACD
11.ABC
【分析】A选项,计算出样本中心点,代入回归方程,求出;B选项,根据百分位数的定义进行求解;C选项,y与x正相关,C正确;D选项,计算出第六年的借阅量约为6.12万册,D错误.
【详解】A选项,,,
将代入得,,解得,A正确;
B选项,,故从小到大选择第4个数作为75%分位数,
即,故借阅量4.9,5.1,5.5,5.7,5.8的75%分位数为5.7,B正确;
C选项,因为,所以y与x正相关,故y与x的线性相关系数,C正确;
D选项,中,令得,
故第六年的借阅量约为6.12万册,可能比6.12万册多,也可能比6.12万册少,D错误.
故选:ABC
12.CD
【详解】
由题意得==3,==10.11.因为回归直线方程=-0.11x+必过样本点中心(,),即10.11=-0.11×3+,解得=10.44,x与y成负相关,即相关系数r<0,故选项A,B错误,C正确;回归直线方程为=-0.11x+10.44,则当x=6时,=-0.11×6+10.44=9.78(s),即下一次世界纪录在9.78 s左右.
13.
【分析】画出散点图,数形结合得到答案.
【详解】画出散点图如下:
从而可以看出中,.
故答案为:.
14.②③
【详解】
表格数据可得K2的观测值K2≈6.1>5.024,所以由参考数据可知能在犯错误的概率不超过0.025的前提下认为药物有效,故②正确;又6.1<6.635,所以由参考数据知不能在犯错误的概率不超过0.010的前提下认为药物有效,故③正确;由参考数据易知①④错误.
15.0.99
【分析】
根据题意,由相关系数的计算公式代入计算,即可得到结果.
【详解】由题意
.
故答案为:.
16.①②④
【分析】
根据平均数的求解可判断④③,利用最小二乘法求解系数即可判断①②.
【详解】
由表中数据可得,,,
则样本中心为,故直线必过点,故④正确,③错误,
,,
则,①②正确.
故答案为:①②④.
17.(1),相关程度较高
(2);投入至少亿元
【分析】(1)直接通过计算相关系数来进行判断;
(2)先计算回归直线方程,然后再做出预测.
【详解】(1),
,
,
,
所以,所以相关程度较高;
(2)由(1)得,,
所以,,
所以,令,
得,所以研发投入至少亿元.
18.(1)
(2)有的把握认为“学生满意度与性别有关”
(3)
【分析】(1)利用频率分布直方图平均数的求法求解即可;
(2)利用(1)的结论及给定信息得到列联表,再计算的观测值,与临界值表比对作答即可得解;
(3)求出8位业主中男女人数,利用列举法及古典概率公式即可得解.
【详解】(1)根据频率分布直方图知,,
所以此次满意度调查中物业所得的平均分值为分.
(2)由(1)及已知得列联表如下:
不满意 满意 总计
男 18 32 50
女 30 20 50
总计 48 52 100
则的观测值为:,
所以有的把握认为“业主满意度与性别有关”.
(3)由(2)知满意度分值低于70分的业主有48位,其中男士18位,女士30位,
用分层抽样方式抽取8位业主,其中男士3位,女士5位,
记男士为a,b,c,记女士为1,2,3,4,5,
从中随机抽取两位为监督员事件为:,
共计28个基本事件,
其中抽到男女各一人有,共15个基本事件,
所以恰好抽到男女各一人为监督员的概率为.
19.(1)列联表见解析,能认为注射疫苗后小白鼠产生抗体与指标值不小于60有关
(2)109或110
【分析】(1)根据给定的频率分布直方图,计算并填写二列联,计算的观测值作答.
(2)利用独立事件、对立事件的概率求出,再用二项分布的概率公式列出不等式,求解作答.
【详解】(1)由频率分布直方图知,在内有(只),
在内有(只),在内有(只),
在内有(只),在内有(只),
依题意,有抗体且指标值小于60的有50只,而指标值小于60的小白鼠共有(只),
于是指标值小于60且没有抗体的小白鼠有20只,同理指标值不小于60且没有抗体的小白鼠有20只,
所以列联表如下:
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设:注射疫苗后小白鼠产生抗体与指标值不小于60无关联,
由列联表中数据,得,
由的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)令事件“小白鼠第一次注射疫苗产生抗体”,事件小白鼠第二次注射疫苗产生抗体”,
事件“小白鼠注射2次疫苗后产生抗体”,记事件发生的概率分别为,
则,于是,
因此一只小白鼠注射2次疫苗后产生抗体的概率,
依题意,随机变量,则,
因为当时,取最大值,即最大,
于是,即
亦即,整理得,解得,
而是整数,因此或,
所以接受接种试验的人数为109或110.
20.(1)分布列见解析,;
(2)57.
【分析】(1)由题意可知,由二项分布即可求出分布列和期望;
(2)由独立性检验可得到含的不等式,构造函数,利用导数即可求.
【详解】(1)由题意可知,高二学生热爱数学的概率为,热爱数学的学生人数,
则,
,
,
,
故的分布列为:
0 1 2 3
的期望为.
(2)因为根据小概率值的独立性检验,认为热爱数学与学生的年级有关,
所以,
令,则,
所以,
因为的对称轴为,
且当时,,
所以在上恒大于0,
所以在上单调递增,
而,
所以实数的最小值为57.
21.(1)
(2)分布列见解析,2
【分析】(1)令,将指数型回归方程转化为线性回归方程,利用最小二乘法的估计系数公式,即可求得答案;
(2)确定真菌与细菌的数值之比位于区间内的组数,即可确定X的取值,求出每个值对应的概率,即可得分布列,即可求得数学期望.
【详解】(1)由于,故,
令,则,
,
则,,
故,则关于的经验回归方程为;
(2)由已知图表可知从第1组到第8组的真菌(单位:百万个)与细菌(单位:百万个)的数值之比依次为:
,,
故样本中比值位于内的组数有4组,则X的可能取值为:,
则,,
故X的分布列为:
X 0 1 2 3 4
P
则.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.针对2025年第九届亚冬会在哈尔滨举办,校团委对“是否喜欢冰雪运动与学生性别的关系”进行了一次调查,其中被调查的男、女生人数相同,男生中喜欢冰雪运动的人数占男生人数的,女生中喜欢冰雪运动的人数占女生人数的,若依据的独立性检验,认为是否喜欢冰雪运动与学生性别有关,则被调查的学生中男生的人数不可( )
附:.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.48 B.54 C.60 D.66
2.开始吸烟年龄与得肺癌的相对危险度相对应的一组数据为,;每天吸烟的支数与其得肺癌的相对危险度相对应的一组数据为,.用表示变量与之间的线性相关系数,用表示变量与之间的线性相关系数,则下列说法正确的是( )
A. B. C. D.
3.用最小二乘法得到一组数据的线性回归方程为,若,则等于( )
A.53 B.65 C.13 D.11
4.校数学兴趣社团对“学生性别和选学生物学是否有关”作了尝试性调查.其中被调查的男女生人数相同.男生选学生物学的人数占男生人数的,女生选学生物学的人数占女生人数.若有的把握认为选学生物学和性别有关,则调查人数中男生不可能有( )人.
附表:
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
其中,.
A.20 B.30 C.35 D.40
5.某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到两种疗法治疗数据的列联表:
疗法 疗效 合计
未治愈 治愈
甲 15 52 67
乙 6 63 69
合计 21 115 136
经计算得到,根据小概率值的独立性检验(已知独立性检验中),则可以认为( )
A.两种疗法的效果存在差异
B.两种疗法的效果存在差异,这种判断犯错误的概率不超过0.005
C.两种疗法的效果没有差异
D.两种疗法的效果没有差异,这种判断犯错误的概率不超过0.005
6.下列说法错误的是( )
A.若随机变量、满足且,则
B.样本数据,,,,,,,,,的第百分位数为
C.若事件、相互独立,则
D.若、两组成对数据的相关系数分别为、,则组数据的相关性更强
7.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得数据如下表:已知该产品的色度y和色差x之间满足线性相关关系,且,现有一组测量数据为,则该数据的残差为( )
色差x 22 24 26 28
色度y 16 19 20 21
A. B. C. D.
8.某老师很喜欢某APP中的“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数,如下表:
天数 1 2 3 4 5 6 7
一次最多答对题数 14 16 18 21 21 a 27
根据最小二乘法得到关于的回归直线方程为,则( )
A.22 B.23 C.24 D.25
二、多选题
9.某厂近几年陆续购买了几台 A 型机床,该型机床已投入生产的时间x(单位:年)与当年所需要支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7
根据表中的数据可得到经验回归方程为. 则( )
A.
B.y与x的样本相关系数
C.表中维修费用的第60百分位数为6
D.该型机床已投入生产的时间为 10年时,当年所需要支出的维修费用一定是12.38万元
10.下列说法中正确的是( )
A.公式中的和不具有线性相关关系
B.已知变量的对数据为,则回归直线可以不经过点,其中
C.若相关系数的绝对值越接近1,则两个变量的线性相关性越强
D.对于变量与的统计量来说,越大,判断“与有关系”的把握越大
11.某地为响应“扶贫必扶智,扶智就是扶知识、扶技术、扶方法”的号召,建立农业科技图书馆,供农民免费借阅,收集了近5年借阅数据如下表:
年份代码x 1 2 3 4 5
年借阅量y(万册) 4.9 5.1 5.5 5.7 5.8
根据上表,可得y关于x的经验回归方程为,下列结论正确的有( )
A.
B.借阅量4.9,5.1,5.5,5.7,5.8的75%分位数为5.7
C.y与x的线性相关系数
D.第六年的借阅量一定不少于6.12万册
12.(多选)人们常将男子短跑100 m的高水平运动员称为“百米飞人”,表中给出了1968年之前部分男子短跑100 m世界纪录产生的年份和世界纪录的数据:
第x次 1 2 3 4 5
年份 1930 1936 1956 1960 1968
纪录/s 10.30 10.20 10.10 10.00 9.95
如果变量y与x之间具有线性相关关系,设用最小二乘法建立的回归直线方程为=-0.11x+,则下列说法正确的是( )
A.变量y与x之间是正相关关系
B.变量y与x之间的线性相关系数r>0
C.=10.44
D.下一次世界纪录在9.78 s左右
三、填空题
13.某同学在研究变量,之间的相关关系时,得到以下数据:并采用最小二乘法得到了线性回归方程,则 0(填“>”或“<”).
4.8 5.8 7 8.3 9.1
2.8 4.1 7.2 9.1 11.8
14.为检验某种药物预防某一疾病的效果,进行了动物试验,得到如下2×2列联表:
患病 未患病 总计
服用药 10 45 55
没服用药 20 30 50
总计 30 75 105
由上述数据给出下列结论,其中结论正确的是 .(填序号)
① 不能在犯错误的概率不超过0.05的前提下认为药物有效;
② 能在犯错误的概率不超过0.025的前提下认为药物有效;
③ 不能在犯错误的概率不超过0.010的前提下认为药物有效;
④ 能在犯错误的概率不超过0.005的前提下认为药物有效.
15.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是正相关,其相关系数 (结果保留两位小数).
16.某公司为了增加某商品的销售利润,调查了该商品投入的广告费用:(单位:万元)与销售利润(单位:万元)的相关数据,如表所示,根据表中数据,得到经验回归方程,则下列命题正确的是 (请填写序号)
广告费用 3 4 5 8
销售利润 4 5 7 8
①; ②;③直线必过点;④直线必过点
四、解答题
17.新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.某中医药企业根据市场调研与模拟,得到研发投入(亿元)与产品收益(亿元)的数据统计如下:
研发投入x(亿元) 1 2 3 4 5
产品收益y(亿元) 3 7 9 10 11
(1)计算的相关系数,并判断是否可以认为研发投入与产品收益具有较高的线性相关程度?(若,则线性相关程度一般,若,则线性相关程度较高)
(2)求出关于的线性回归方程,并预测若想收益超过50(亿元)则需研发投入至少多少亿元?(结果保留一位小数)
参考数据:;
附:相关系数公式:;
回归直线方程的斜率.
18.某校为了让学生有一个良好的学习环境,特制定学生满意度调查表,调查表分值满分为100分.工作人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如图.
(1)估计此次满意度调查所得的平均分值(同一组中的数据用该组区间的中点值为代表);
(2)在选取的100位学生中,男女生人数相同,规定分值在(1)中的以上为满意,低于为不满意,据统计有32位男生满意.据此判断是否有的把握认为“学生满意度与性别有关”?
(3)在(2)的条件下,学校从满意度分值低于分的学生中抽取部分进行座谈,先用分层抽样的方式选出8位学生,再从中随机抽取2人,求恰好抽到男女生各一人的概率.
附:,其中.
19.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验,研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[0,20),[20,40),[40,60),[60,80)分组,绘制频率分布直方图如图所示,试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表(单位:只),并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.用频率估计概率,记一只小白鼠注射2次疫苗后产生抗体的概率p,并以p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n个人注射2次疫苗后产生抗体的数量为随机变量X.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数n.
参考公式:(其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
20.某市教育局为了调查学生热爱数学是否与学生的年级有关,从全市随机抽取了50位高二学生和位高三学生进行调查,每位学生对“是否热爱数学”提出“热爱”或“不热爱”的观点,得到如下数据:
观点 高二 高三
热爱 30 20
不热爱 20
(1)以该50名高二学生热爱数学的频率作为全市高二学生热爱数学的概率,从全市的高二学生中随机抽取3名学生,记为这3名学生中热爱数学的学生人数,求的分布列和期望;
(2)若根据小概率值的独立性检验,认为热爱数学与学生的年级有关,求实数的最小值.
附:.
0.050 0.010 0.001
3.841 6.635 10.828
21.土壤食物网对有机质的分解有两条途径,即真菌途径和细菌途径.在不同的土壤生态系统中,由于提供能源的有机物其分解的难易程度不同,这两条途径所起的作用也不同.以细菌分解途径为主导的土壤,有机质降解快,氮矿化率高,有利于养分供应,以真菌途径为主的土壤,氮和能量转化比较缓慢,有利于有机质存财和氮的固持.某生物实验小组从一种土壤数据中随机抽查并统计了8组数据,如下表所示:
编号 1 2 3 4 5 6 7 8
细菌百万个 70 80 90 100 110 120 130 140
真菌百万个 8.0 10.0 12.5 15.0 17.5 21.0 27.0 39.0
其散点图如下,散点大致分布在指数型函数的图象附近.
(1)求关于的经验回归方程(系数精确到0.01);
(2)在做土壤相关的生态环境研究时,细菌与真菌的比值能够反映土壤的碳氮循环.以样本的频率估计总体分布的概率,若该实验小组随机抽查8组数据,再从中任选4组,记真菌(单位:百万个)与细菌(单位:百万个)的数值之比位于区间内的组数为,求的分布列与数学期望.
附:经验回归方程的斜率和截距的最小二乘估计公式分别为,
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】根据已知条件设男生人数为,结合独立性检验公式得出不等式,根据的取值,即可求解.
【详解】设男生人数为,因为被调查的男、女生人数相同,
所以女生人数也为,根据题意列出列联表:
男生 女生 合计
喜欢冰雪运动
不喜欢冰雪运动
合计
则,
因为依据的独立性检验,认为是否喜欢冰雪运动与学生性别有关,
所以,即,解得,又,
所以B、C、D正确,A错误.
故选:A
2.D
【分析】借助线性相关系数的定义判断即可得.
【详解】由与相对应的数据可得,随的增大而减小,呈负相关,故,
由与相对应的数据可得,随的增大而增大,呈正相关,故,
故.
故选:D.
3.B
【分析】根据题意,由条件可得,由线性回归方程必过样本中心,代入计算,即可得到结果.
【详解】因为,则,代入可得,
所以.
故选:B
4.A
【分析】借助卡方计算即可得.
【详解】设总人数为,则男生选学生物学的人数为,女生选生物学的人数为,
则,
即,又为的倍数,故男生最少有人.
故选:A.
5.C
【分析】根据条件可得列联表,计算的值,结合临界值表可得结论.
【详解】零假设为:疗法与疗效独立,即两种疗法效果没有差异.
根据列联表中的数据,,根据小概率值的独立性检验,
没有充分证据推断不成立,
因此可以认为成立,
即认为两种疗法效果没有差异.
故选:C.
6.D
【分析】根据方差的性质判断A,根据百分位数计算规则判断B,根据相互独立事件及条件概率概率公式判断C,根据相关系数的概念判断D.
【详解】对于A:因为且,所以,故A正确;
对于B:因为,所以第百分位数为从小到大排列的第个数,即为,故B正确;
对于C:若事件、相互独立,则,
所以,故C正确;
对于D:若、两组成对数据的相关系数分别为、,
因为,所以组数据的相关性更强,故D错误.
故选:D
7.D
【分析】根据题意,由回归直线方程过样本中心点,即可得到,然后代入计算,即可得到结果.
【详解】由题意可知,,,
将代入,即,解得,
所以,当时,,
所以该数据的残差为.
故选:D.
8.B
【分析】求出回归中心,代入回归方程求解即可.
【详解】因为,,所以,解得.
故选:B.
9.ABC
【分析】对A,计算出样本中心,代入方程计算出,对B,根据相关系数的概念可判断,对C,根据百分位数的定义求解,对D,根据回归分析概念判断.
【详解】根据题意可得,,,
所以样本中心点为,
对于A,将样本中心点代入回归方程,可得,故A正确;
对于B,由表中数据可得随着增大而增大,与正相关,所以相关系数,故B正确;
对于C,维修费用从小到大依次为,第60百分位数为,故C正确;
对于D,根据回归分析的概念,机床投入生产的时间为 10年时,所需要支出的维修费用大概是12.38万元,故D错误.
故选:ABC.
10.ACD
【分析】A选项,根据线性相关的定义进行判断;B选项,回归直线一定经过样本中心点;C选项,由相关系数的性质进行判断;D选项,根据的定义判断D正确.
【详解】A选,公式中的和为二次函数关系,故不具有线性相关关系,A正确;
B选项,回归直线一定经过样本中心点,即,B错误;
C选项,若相关系数的绝对值越接近1,则两个变量的线性相关性越强,C正确;
D选项,对于变量与的统计量来说,越大,判断“与有关系”的把握越大,D正确.
故选:ACD
11.ABC
【分析】A选项,计算出样本中心点,代入回归方程,求出;B选项,根据百分位数的定义进行求解;C选项,y与x正相关,C正确;D选项,计算出第六年的借阅量约为6.12万册,D错误.
【详解】A选项,,,
将代入得,,解得,A正确;
B选项,,故从小到大选择第4个数作为75%分位数,
即,故借阅量4.9,5.1,5.5,5.7,5.8的75%分位数为5.7,B正确;
C选项,因为,所以y与x正相关,故y与x的线性相关系数,C正确;
D选项,中,令得,
故第六年的借阅量约为6.12万册,可能比6.12万册多,也可能比6.12万册少,D错误.
故选:ABC
12.CD
【详解】
由题意得==3,==10.11.因为回归直线方程=-0.11x+必过样本点中心(,),即10.11=-0.11×3+,解得=10.44,x与y成负相关,即相关系数r<0,故选项A,B错误,C正确;回归直线方程为=-0.11x+10.44,则当x=6时,=-0.11×6+10.44=9.78(s),即下一次世界纪录在9.78 s左右.
13.
【分析】画出散点图,数形结合得到答案.
【详解】画出散点图如下:
从而可以看出中,.
故答案为:.
14.②③
【详解】
表格数据可得K2的观测值K2≈6.1>5.024,所以由参考数据可知能在犯错误的概率不超过0.025的前提下认为药物有效,故②正确;又6.1<6.635,所以由参考数据知不能在犯错误的概率不超过0.010的前提下认为药物有效,故③正确;由参考数据易知①④错误.
15.0.99
【分析】
根据题意,由相关系数的计算公式代入计算,即可得到结果.
【详解】由题意
.
故答案为:.
16.①②④
【分析】
根据平均数的求解可判断④③,利用最小二乘法求解系数即可判断①②.
【详解】
由表中数据可得,,,
则样本中心为,故直线必过点,故④正确,③错误,
,,
则,①②正确.
故答案为:①②④.
17.(1),相关程度较高
(2);投入至少亿元
【分析】(1)直接通过计算相关系数来进行判断;
(2)先计算回归直线方程,然后再做出预测.
【详解】(1),
,
,
,
所以,所以相关程度较高;
(2)由(1)得,,
所以,,
所以,令,
得,所以研发投入至少亿元.
18.(1)
(2)有的把握认为“学生满意度与性别有关”
(3)
【分析】(1)利用频率分布直方图平均数的求法求解即可;
(2)利用(1)的结论及给定信息得到列联表,再计算的观测值,与临界值表比对作答即可得解;
(3)求出8位业主中男女人数,利用列举法及古典概率公式即可得解.
【详解】(1)根据频率分布直方图知,,
所以此次满意度调查中物业所得的平均分值为分.
(2)由(1)及已知得列联表如下:
不满意 满意 总计
男 18 32 50
女 30 20 50
总计 48 52 100
则的观测值为:,
所以有的把握认为“业主满意度与性别有关”.
(3)由(2)知满意度分值低于70分的业主有48位,其中男士18位,女士30位,
用分层抽样方式抽取8位业主,其中男士3位,女士5位,
记男士为a,b,c,记女士为1,2,3,4,5,
从中随机抽取两位为监督员事件为:,
共计28个基本事件,
其中抽到男女各一人有,共15个基本事件,
所以恰好抽到男女各一人为监督员的概率为.
19.(1)列联表见解析,能认为注射疫苗后小白鼠产生抗体与指标值不小于60有关
(2)109或110
【分析】(1)根据给定的频率分布直方图,计算并填写二列联,计算的观测值作答.
(2)利用独立事件、对立事件的概率求出,再用二项分布的概率公式列出不等式,求解作答.
【详解】(1)由频率分布直方图知,在内有(只),
在内有(只),在内有(只),
在内有(只),在内有(只),
依题意,有抗体且指标值小于60的有50只,而指标值小于60的小白鼠共有(只),
于是指标值小于60且没有抗体的小白鼠有20只,同理指标值不小于60且没有抗体的小白鼠有20只,
所以列联表如下:
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设:注射疫苗后小白鼠产生抗体与指标值不小于60无关联,
由列联表中数据,得,
由的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)令事件“小白鼠第一次注射疫苗产生抗体”,事件小白鼠第二次注射疫苗产生抗体”,
事件“小白鼠注射2次疫苗后产生抗体”,记事件发生的概率分别为,
则,于是,
因此一只小白鼠注射2次疫苗后产生抗体的概率,
依题意,随机变量,则,
因为当时,取最大值,即最大,
于是,即
亦即,整理得,解得,
而是整数,因此或,
所以接受接种试验的人数为109或110.
20.(1)分布列见解析,;
(2)57.
【分析】(1)由题意可知,由二项分布即可求出分布列和期望;
(2)由独立性检验可得到含的不等式,构造函数,利用导数即可求.
【详解】(1)由题意可知,高二学生热爱数学的概率为,热爱数学的学生人数,
则,
,
,
,
故的分布列为:
0 1 2 3
的期望为.
(2)因为根据小概率值的独立性检验,认为热爱数学与学生的年级有关,
所以,
令,则,
所以,
因为的对称轴为,
且当时,,
所以在上恒大于0,
所以在上单调递增,
而,
所以实数的最小值为57.
21.(1)
(2)分布列见解析,2
【分析】(1)令,将指数型回归方程转化为线性回归方程,利用最小二乘法的估计系数公式,即可求得答案;
(2)确定真菌与细菌的数值之比位于区间内的组数,即可确定X的取值,求出每个值对应的概率,即可得分布列,即可求得数学期望.
【详解】(1)由于,故,
令,则,
,
则,,
故,则关于的经验回归方程为;
(2)由已知图表可知从第1组到第8组的真菌(单位:百万个)与细菌(单位:百万个)的数值之比依次为:
,,
故样本中比值位于内的组数有4组,则X的可能取值为:,
则,,
故X的分布列为:
X 0 1 2 3 4
P
则.
答案第1页,共2页
答案第1页,共2页
同课章节目录
