高中数学人教B版(2019)选择性必修第一册 第1章 1.1.1 空间向量及其运算 同步练习(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)选择性必修第一册 第1章 1.1.1 空间向量及其运算 同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 423.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 08:44:23 | ||
图片预览




文档简介
人教B版(2019)数学高中选择性必修第一册
1.1.1 空间向量及其运算
一.选择题
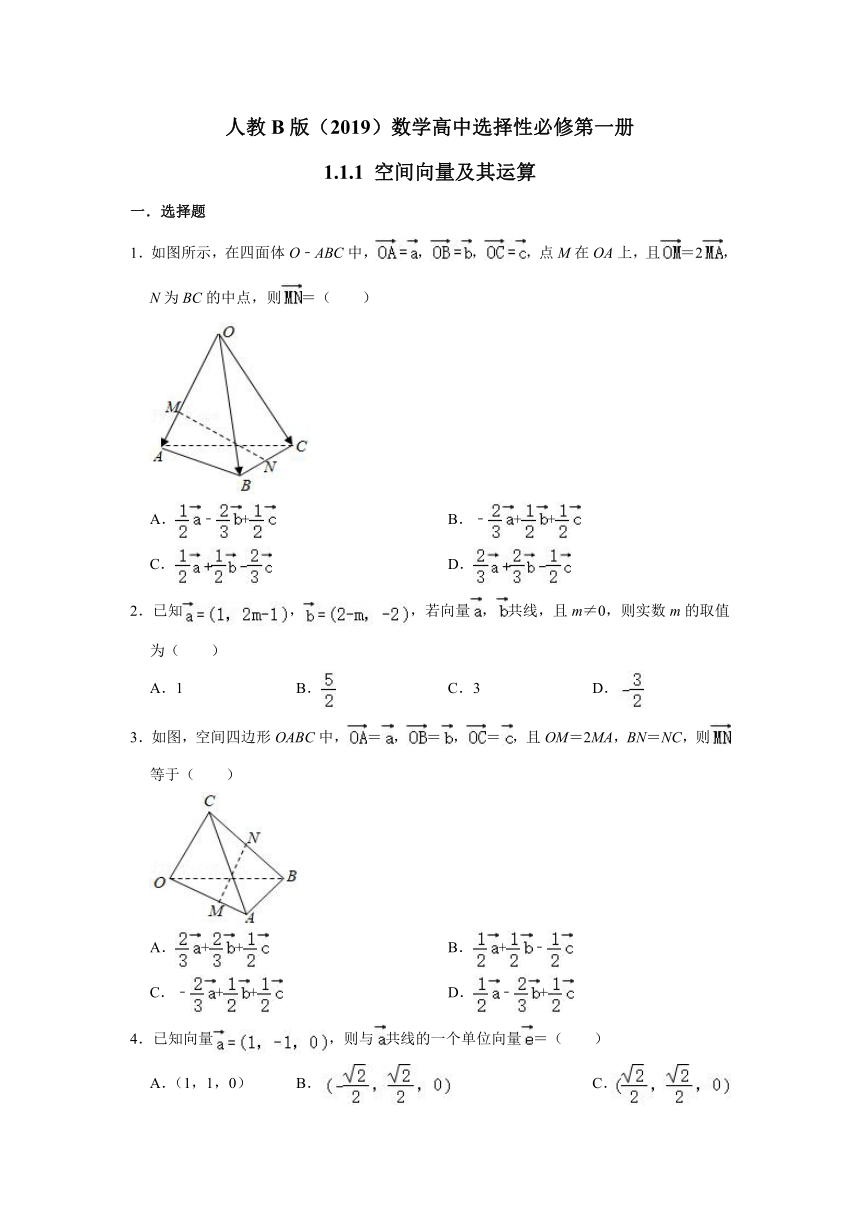
1.如图所示,在四面体O﹣ABC中,,,,点M在OA上,且=2,N为BC的中点,则=( )
A.﹣+ B.﹣++
C. D.
2.已知,,若向量,共线,且m≠0,则实数m的取值为( )
A.1 B. C.3 D.
3.如图,空间四边形OABC中,=,=,=,且OM=2MA,BN=NC,则等于( )
A.++ B.+﹣
C.﹣++ D.﹣+
4.已知向量,则与共线的一个单位向量=( )
A.(1,1,0) B. C. D.(0,0,1)
5.如图所示,在三棱锥D﹣ABC中,E,F分别是AB,BC的中点,则等于( )
A. B. C. D.
6.已知空间向量=(2,﹣1,1),=(﹣4,x,y),∥,则x﹣y=( )
A.4 B.﹣4 C.0 D.2
7.已知向量=(2,1,4),=(1,0,2),且+与k﹣互相垂直,则k的值是( )
A.1 B. C. D.
8.已知空间向量,则向量在坐标平面xOy上的投影向量是( )
A.(0,2,1) B.(2,1,0) C.(0,1,﹣3) D.(2,0,﹣3)
9.已知空间向量=(2,3,6),=(3,﹣4,1),则<,>=( )
A. B. C. D.
10.已知空间向量=(1,﹣1,0),=(1,﹣1,1),则|+|=( )
A.3 B. C. D.
二.填空题
11.在长方体ABCD﹣A1B1C1D1中,M,N分别是BC,C1D1的中点,若=a+b+c,则a﹣b﹣c=
12.已知=(1,0,﹣1),=(2,1,1),则2﹣= .
13.已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= .
14.已知空间向量,则向量在坐标平面Oxz上的投影向量是 .
15.已知P,A,B,C四点共面且对于空间任意一点O,都有=2,则t= .
三.解答题
16.如图所示,已知几何体ABCD﹣A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的点,且C1N=C1B,设=x+y+z,试求x,y,z的值.
17.如图所示,在三棱柱ABC﹣A1B1C1中,M是BB1中点,化简下列各式:
(1);
(2);
(3).
18.如图所示,已知斜三棱柱ABC﹣A1B1C1,点M,N分别在AC1和BC上,且满足=k,=k(0≤k≤1),判断向量是否与向量,共面.
人教B版(2019)数学高中选择性必修第一册
1.1.1 空间向量及其运算
参考答案与试题解析
一.选择题
1.【考点】空间向量及其线性运算.
【解答】解:连接ON,
∵N是BC的中点,∴=,
∵=2,∴=,
∴==﹣=﹣++,
故选:B.
2.【考点】共线向量与共面向量;平面向量共线(平行)的坐标表示.
【解答】解:∵,,若向量,共线,且m≠0,
∴1×(﹣2)﹣(2m﹣1)(2﹣m)=0,
即2m2﹣5m=0,解得m=0(舍)或m=.
故选:B.
3.【考点】空间向量及其线性运算.
【解答】解:由题意知,=++
=+(﹣)+
=﹣++(﹣)
=﹣++
=﹣++.
故选:C.
4.【考点】空间向量及其线性运算.
【解答】解:向量,
则与共线的单位向量为=±=±(,,0)=±(,﹣,0).
所以=(,﹣,0)或(﹣,,0).
故选:B.
5.【考点】共线向量与共面向量.
【解答】解:在三棱锥D﹣ABC中,E,F分别是AB,BC的中点,则,;
所以.
故选:D.
6.【考点】共线向量与共面向量;向量的数量积判断向量的共线与垂直.
【解答】解:∵=(2,﹣1,1),=(﹣4,x,y),∥,
∴==,
∴x=2,y=﹣2,
∴x﹣y=4,
故选:A.
7.【考点】空间向量的数量积运算.
【解答】解:+=(3,1,6),k﹣=(2k﹣1,k,4k﹣2),
∵+与k﹣互相垂直,∴3(2k﹣1)+k+6(4k﹣2)=0,
解得k=,
故选:D.
8.【考点】空间向量的数量积运算.
【解答】解:∵,
∴在坐标平面xOy上的投影向量是(2,1,0).
故选:B.
9.【考点】空间向量的夹角与距离求解公式;空间向量的数量积运算.
【解答】解:∵空间向量=(2,3,6),=(3,﹣4,1),
∴cos<>==0,则<,>=.
故选:A.
10.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵空间向量=(1,﹣1,0),=(1,﹣1,1),
∴=(2,﹣2,1),
|+|==3.
故选:A.
二.填空题
11.【考点】空间向量及其线性运算.
【解答】解:在长方体ABCD﹣A1B1C1D1中,M,N分别是BC,C1D1的中点,
=
=+﹣
=﹣,
∵=a+b+c,
∴a=﹣,b=,c=1,
∴a﹣b﹣c=﹣2.
故答案为:﹣2.
12.【考点】空间向量及其线性运算;空间向量运算的坐标表示.
【解答】解:由
可得
故答案为:(0,﹣1,﹣3).
13.【考点】共线向量与共面向量.
【解答】解:=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,
若直线l1∥l2,则,
∴,则x=﹣2,y=1.
∴x+y=﹣2+1=﹣1.
故答案为:﹣1.
14.【考点】空间向量的数量积运算.
【解答】解:根据空间中点的坐标确定方法知,
空间中点A(1,﹣2,﹣3)在坐标平面Oxz上的投影坐标,纵坐标为0,横坐标与竖坐标不变.
所以空间向量=(1,﹣2,﹣3)在坐标平面Oxz上的投影向量是:(1,0,﹣3).
故答案为:(1,0,﹣3).
15.【考点】空间向量的夹角与距离求解公式.
【解答】解:=﹣=,=﹣=2,=﹣=2,
∵P,A,B,C四点共面,∴存在m,n∈R使得=m+n,
∴=m(2)+n[2]=(2m+2n)+n+(mt+nt﹣n),
∴,解得m=﹣,n=1,t=﹣2.
故答案为:﹣2.
三.解答题
16.【考点】空间向量及其线性运算.
【解答】解:设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的点,且C1N=C1B,
根据向量的运算:=,
故x=.
17.【考点】空间向量及其线性运算.
【解答】解:(1)=;
(2)==;
(3)==.
18.【考点】共线向量与共面向量.
【解答】解:∵==k()=(1﹣k)+k.
=k=k(),
∴==(1﹣k)﹣,
∴向量与向量,共面.
1.1.1 空间向量及其运算
一.选择题
1.如图所示,在四面体O﹣ABC中,,,,点M在OA上,且=2,N为BC的中点,则=( )
A.﹣+ B.﹣++
C. D.
2.已知,,若向量,共线,且m≠0,则实数m的取值为( )
A.1 B. C.3 D.
3.如图,空间四边形OABC中,=,=,=,且OM=2MA,BN=NC,则等于( )
A.++ B.+﹣
C.﹣++ D.﹣+
4.已知向量,则与共线的一个单位向量=( )
A.(1,1,0) B. C. D.(0,0,1)
5.如图所示,在三棱锥D﹣ABC中,E,F分别是AB,BC的中点,则等于( )
A. B. C. D.
6.已知空间向量=(2,﹣1,1),=(﹣4,x,y),∥,则x﹣y=( )
A.4 B.﹣4 C.0 D.2
7.已知向量=(2,1,4),=(1,0,2),且+与k﹣互相垂直,则k的值是( )
A.1 B. C. D.
8.已知空间向量,则向量在坐标平面xOy上的投影向量是( )
A.(0,2,1) B.(2,1,0) C.(0,1,﹣3) D.(2,0,﹣3)
9.已知空间向量=(2,3,6),=(3,﹣4,1),则<,>=( )
A. B. C. D.
10.已知空间向量=(1,﹣1,0),=(1,﹣1,1),则|+|=( )
A.3 B. C. D.
二.填空题
11.在长方体ABCD﹣A1B1C1D1中,M,N分别是BC,C1D1的中点,若=a+b+c,则a﹣b﹣c=
12.已知=(1,0,﹣1),=(2,1,1),则2﹣= .
13.已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= .
14.已知空间向量,则向量在坐标平面Oxz上的投影向量是 .
15.已知P,A,B,C四点共面且对于空间任意一点O,都有=2,则t= .
三.解答题
16.如图所示,已知几何体ABCD﹣A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的点,且C1N=C1B,设=x+y+z,试求x,y,z的值.
17.如图所示,在三棱柱ABC﹣A1B1C1中,M是BB1中点,化简下列各式:
(1);
(2);
(3).
18.如图所示,已知斜三棱柱ABC﹣A1B1C1,点M,N分别在AC1和BC上,且满足=k,=k(0≤k≤1),判断向量是否与向量,共面.
人教B版(2019)数学高中选择性必修第一册
1.1.1 空间向量及其运算
参考答案与试题解析
一.选择题
1.【考点】空间向量及其线性运算.
【解答】解:连接ON,
∵N是BC的中点,∴=,
∵=2,∴=,
∴==﹣=﹣++,
故选:B.
2.【考点】共线向量与共面向量;平面向量共线(平行)的坐标表示.
【解答】解:∵,,若向量,共线,且m≠0,
∴1×(﹣2)﹣(2m﹣1)(2﹣m)=0,
即2m2﹣5m=0,解得m=0(舍)或m=.
故选:B.
3.【考点】空间向量及其线性运算.
【解答】解:由题意知,=++
=+(﹣)+
=﹣++(﹣)
=﹣++
=﹣++.
故选:C.
4.【考点】空间向量及其线性运算.
【解答】解:向量,
则与共线的单位向量为=±=±(,,0)=±(,﹣,0).
所以=(,﹣,0)或(﹣,,0).
故选:B.
5.【考点】共线向量与共面向量.
【解答】解:在三棱锥D﹣ABC中,E,F分别是AB,BC的中点,则,;
所以.
故选:D.
6.【考点】共线向量与共面向量;向量的数量积判断向量的共线与垂直.
【解答】解:∵=(2,﹣1,1),=(﹣4,x,y),∥,
∴==,
∴x=2,y=﹣2,
∴x﹣y=4,
故选:A.
7.【考点】空间向量的数量积运算.
【解答】解:+=(3,1,6),k﹣=(2k﹣1,k,4k﹣2),
∵+与k﹣互相垂直,∴3(2k﹣1)+k+6(4k﹣2)=0,
解得k=,
故选:D.
8.【考点】空间向量的数量积运算.
【解答】解:∵,
∴在坐标平面xOy上的投影向量是(2,1,0).
故选:B.
9.【考点】空间向量的夹角与距离求解公式;空间向量的数量积运算.
【解答】解:∵空间向量=(2,3,6),=(3,﹣4,1),
∴cos<>==0,则<,>=.
故选:A.
10.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵空间向量=(1,﹣1,0),=(1,﹣1,1),
∴=(2,﹣2,1),
|+|==3.
故选:A.
二.填空题
11.【考点】空间向量及其线性运算.
【解答】解:在长方体ABCD﹣A1B1C1D1中,M,N分别是BC,C1D1的中点,
=
=+﹣
=﹣,
∵=a+b+c,
∴a=﹣,b=,c=1,
∴a﹣b﹣c=﹣2.
故答案为:﹣2.
12.【考点】空间向量及其线性运算;空间向量运算的坐标表示.
【解答】解:由
可得
故答案为:(0,﹣1,﹣3).
13.【考点】共线向量与共面向量.
【解答】解:=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,
若直线l1∥l2,则,
∴,则x=﹣2,y=1.
∴x+y=﹣2+1=﹣1.
故答案为:﹣1.
14.【考点】空间向量的数量积运算.
【解答】解:根据空间中点的坐标确定方法知,
空间中点A(1,﹣2,﹣3)在坐标平面Oxz上的投影坐标,纵坐标为0,横坐标与竖坐标不变.
所以空间向量=(1,﹣2,﹣3)在坐标平面Oxz上的投影向量是:(1,0,﹣3).
故答案为:(1,0,﹣3).
15.【考点】空间向量的夹角与距离求解公式.
【解答】解:=﹣=,=﹣=2,=﹣=2,
∵P,A,B,C四点共面,∴存在m,n∈R使得=m+n,
∴=m(2)+n[2]=(2m+2n)+n+(mt+nt﹣n),
∴,解得m=﹣,n=1,t=﹣2.
故答案为:﹣2.
三.解答题
16.【考点】空间向量及其线性运算.
【解答】解:设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的点,且C1N=C1B,
根据向量的运算:=,
故x=.
17.【考点】空间向量及其线性运算.
【解答】解:(1)=;
(2)==;
(3)==.
18.【考点】共线向量与共面向量.
【解答】解:∵==k()=(1﹣k)+k.
=k=k(),
∴==(1﹣k)﹣,
∴向量与向量,共面.
