第十八章 平行四边形单元测试卷(含解析)
文档属性
| 名称 | 第十八章 平行四边形单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 08:58:12 | ||
图片预览


文档简介
人教版八年级下册数学单元测试卷
第十八章 平行四边形
(本试卷三个大题,25个小题。满分150分,考试时间120分钟。)
姓名 班级 学号 成绩
一、选择题(本题共12个小题,每小题3分,共36分;每个小题只有一项符合题意。)
1.菱形ABCD的对角线AC=6,BD=8,那么边AB的长度 是( )
A.10 B.5 C. D.
2.在平行四边形中,若,则( )
A. B. C. D.
3.将一张边长分别为8、6的矩形纸片ABCD折叠,使点C与A重合,则折痕的长为( )
A.6 B.6.5 C.7.5 D.10
4.下列说法中错误的是( )
A.直角三角形斜边上的中线等于斜边的一半
B.等底等高三角形的面积相等
C.三角形的中位线平行于第三边,并且等于第三边的一半
D.如果三角形两条边的长分别是a、b,第三边长为c,则有a2+b2=c2
5.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )
A.6cm B.5cm C. D.
6.如图,在菱形中,,则的度数为( )
A.
B.
C.
D.
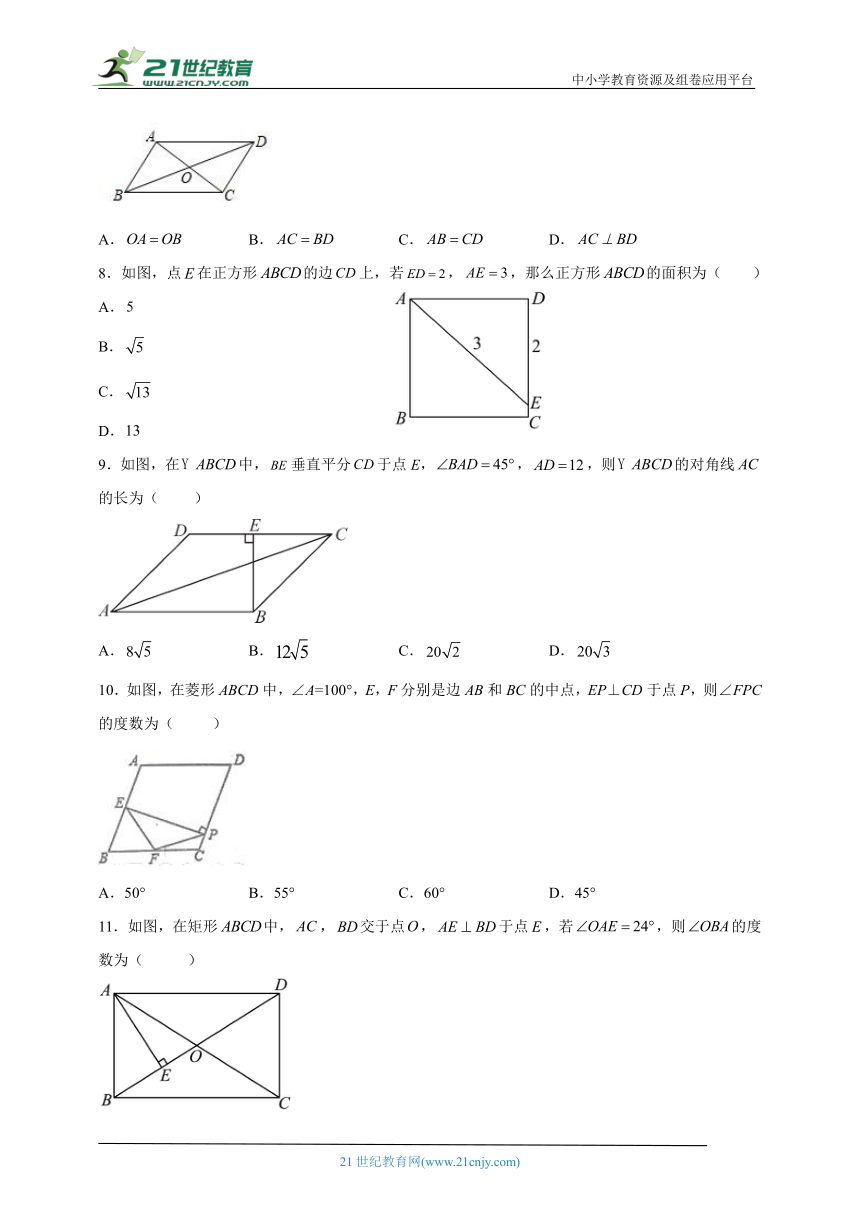
7.如图,的对角线、交于,则下列结论一定成立的是( )
A. B. C. D.
8.如图,点在正方形的边上,若,,那么正方形的面积为( )
A.
B.
C.
D.
9.如图,在中,垂直平分于点E,,,则的对角线的长为( )
A. B. C. D.
10.如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.50° B.55° C.60° D.45°
11.如图,在矩形中,,交于点,于点,若,则的度数为( )
A. B. C. D.
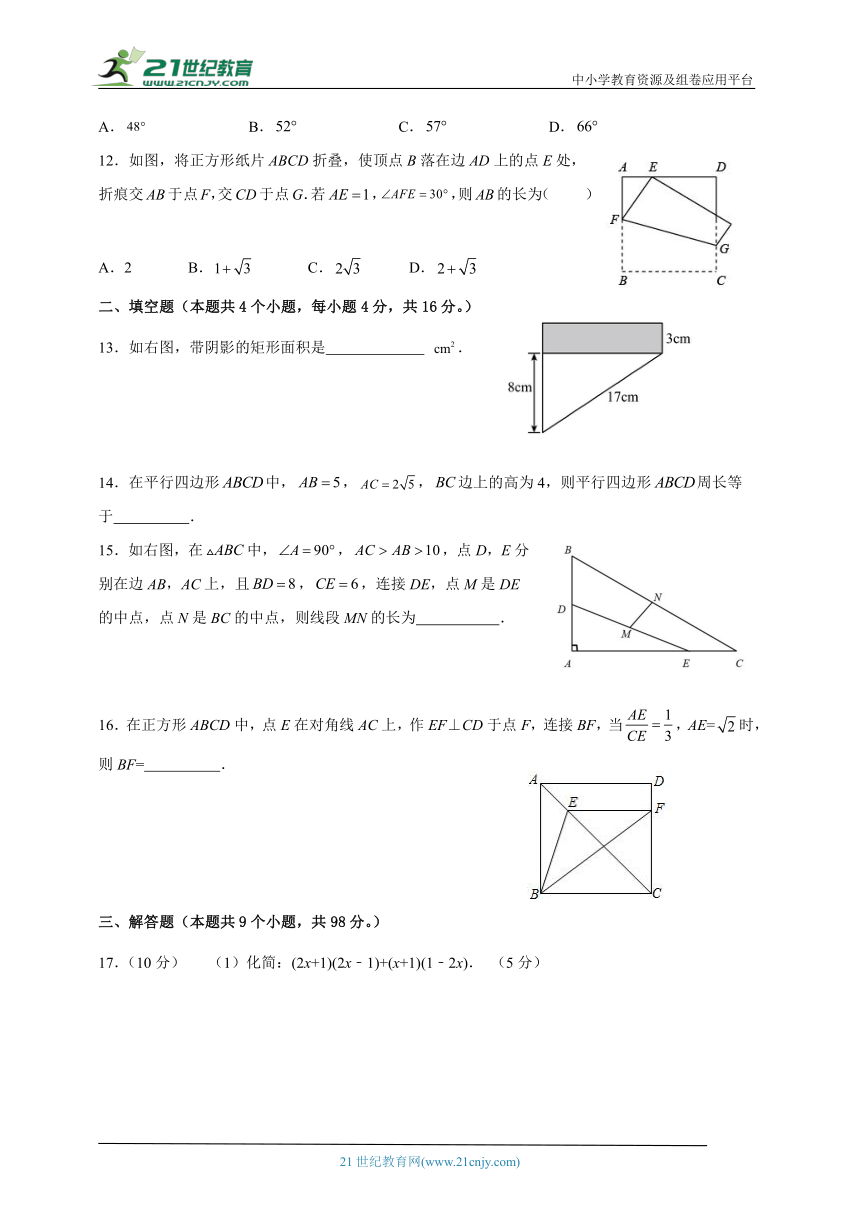
12.如图,将正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,折痕交AB于点F,交CD于点G.若,,则AB的长为( )
A.2 B. C. D.
二、填空题(本题共4个小题,每小题4分,共16分。)
13.如右图,带阴影的矩形面积是 .
14.在平行四边形中,,,边上的高为4,则平行四边形周长等于 .
15.如右图,在中,,,点D,E分别在边AB,AC上,且,,连接DE,点M是DE的中点,点N是BC的中点,则线段MN的长为 .
16.在正方形ABCD中,点E在对角线AC上,作EF⊥CD于点F,连接BF,当,AE=时,则BF= .
三、解答题(本题共9个小题,共98分。)
17.(10分) (1)化简:(2x+1)(2x﹣1)+(x+1)(1﹣2x). (5分)
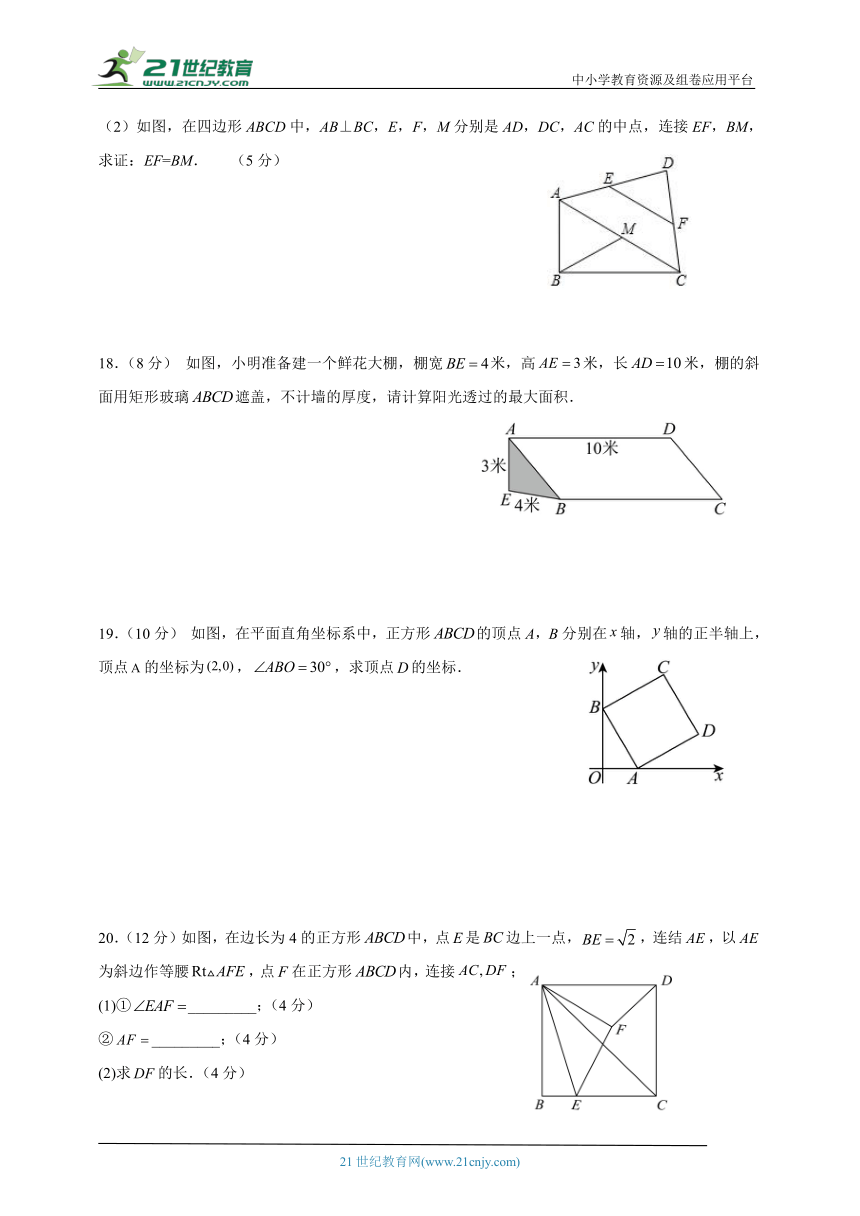
(2)如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证:EF=BM. (5分)
18.(8分) 如图,小明准备建一个鲜花大棚,棚宽米,高米,长米,棚的斜面用矩形玻璃遮盖,不计墙的厚度,请计算阳光透过的最大面积.
19.(10分) 如图,在平面直角坐标系中,正方形的顶点A,B分别在轴,轴的正半轴上,顶点的坐标为,,求顶点的坐标.
20.(12分)如图,在边长为4的正方形中,点是边上一点,,连结,以为斜边作等腰,点在正方形内,连接;
(1)①_________;(4分)
②_________;(4分)
(2)求的长.(4分)
21.(10分)如图,平行四边形中,的平分线交于E,的平分线交于点F.
(1)求证:;(5分)
(2)若,,,求的长.(5分)
22.(12分)如图,边长为4的正方形ABCD中,点E在AD上,△ABE逆时针旋转一定角度后得到△ADF,延长BE交DF于点G,若AE=3.
(1)指出旋转中心和旋转角度;(4分)
(2)求证:BG⊥DF;(4分)
(3)求线段GE的长.(4分)
23.(12分) 已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
(1)说明:△BCE≌△DCF;
(2)OG与BF有什么数量关系?说明你的结论;(6分)
(3)若BC·BD=,求正方形ABCD的面积.(6分)
24.(12分) 如图,在中,点是边上的一个动点(点不与、两点重合),过点作直线,直线与的平分线相交于点,与(的外角)的平分线相交于点.
(1)与相等吗?为什么?(4分)
(2)探究:当点运动到何处时,四边形是矩形?并证明你的结论.(4分)
(3)在(2)中当等于多少时,四边形为正方形(不要求说理由)(4分)
25.(12分)如图1所示,平行四边形是苏州乐园某主题区域的平面示意图,A,B,C,D分别是该区域的四个入口,两条主干道,交于点O,请你帮助苏州乐园的管理人员解决以下问题:
(1)若,你能判断的形状吗?请说明理由.(4分)
(2)在(1)的条件下,如图2,乐园管理人员为提升游客游览的体验感,准备修建三条绿道,其中点M在上,点N在上,且(点M与点O,B不重合),并计划在与两块绿地所在区域种植花期长久的马鞭草,求种植马鞭草区域的面积.(4分)
中小学教育资源及组卷应用平台
(3)若将该区域扩大,如图3,此时,修建(2)中的绿道每千米费用为4万元,请你计算修建这三条绿道投入资金的最小值.(4分)21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长.
【详解】解:根据题意,设对角线AC、BD相较于O,
∵四边形ABCD是菱形.
∴AO=AC=3,BO=BD=4,且AO⊥BO,
∴AB=5,
故选B.
【点睛】本题考查菱形的性质,要熟练掌握菱形对角线的性质,及勾股定理的灵活运用.
2.B
【分析】根据平行四边形的性质,即可求解.
【详解】解:∵四边形是平行四边形,
∴.
故选B.
【点睛】本题主要考查了平行四边形的性质,熟练掌握平行四边形的对角相等是解题的关键.
3.C
【详解】如图,设折痕为EF,由题意可知:EF垂直平分AC,作EM⊥BC于M,
∴CE=AE,
设DE为x,则CE=AE=8-x,在Rt△CDE中,由勾股定理可得:,
解得:,
∴DE=CM=,
同理可得:BF=,
∴MF=BC-BF-CM=,
在Rt△EFM中,由勾股定理可得:.
故选C.
点睛:在有关矩形的折叠问题中,需注意两个问题:(1)折叠前后的两个对应图形是关于折痕对称的,要充分利用轴对称的性质;(2)把已知量和要求的量集中到一个直角三角形中,利用勾股定理建立方程来解题.
4.D
【分析】根据三角性有关的性质可逐一分析选项,即可得到答案.
【详解】A项正确,直角三角形斜边上的中线等于斜边的一半;B项正确,等底等高三角形的面积相等;C项正确,三角形的中位线平行于第三边,并且等于第三边的一半;D项错误如果三角形两条边的长分别是a、b,第三边长为c,则不一定是a2+b2=c2,有可能不是直角三角形.
【点睛】本题考查了三角形的的性质、三角形的面积及勾股定理相关的知识,学生针对此题需要认真掌握相关定理,即可求解.
5.B
【详解】∵菱形的两条对角线分别为5cm和10cm,
∴菱形的面积为:(cm2),
设正方形的边长为cm,则,解得:(cm).
故选B.
6.B
【分析】根据菱形的对角线平分一组对角,菱形的邻角互补求解即可.
【详解】解:∵在菱形中,,
∴,
∴,
故选:B.
【点睛】本题考查了菱形的性质,熟知菱形的对角线平分一组对角,菱形的邻角互补是解题的关键.
7.C
【分析】根据平行四边形的性质可直接判断求解.
【详解】解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,AB=CD,
A、OA=OB,不一定成立,故该选项不符合题意;
B、AC=BD,不一定成立,故该选项不符合题意;
C、AB=CD,成立,故该选项符合题意;
D、,不一定成立,故该选项不符合题意;
故选:C.
【点睛】本题主要考查了平行四边形的性质,掌握平行四边形的性质是解题的关键.
8.A
【分析】根据正方形的性质可得,根据勾股定理即可求得,即可求解.
【详解】解:∵四边形是正方形,
∴,
在中,,
∴正方形的面积.
故选:A.
【点睛】本题考查了勾股定理,正方形的性质,熟练掌握正方形的性质和勾股定理是解题的关键.
9.B
【分析】连接交于点F,根据平行四边形和线段垂直平分线的性质可以推出,即可推出,先利用勾股定理求出的长,即可求出的长.
【详解】解:如图,连接交于点F.
∵垂直平分,
∴,
∵四边形为平行四边形,
∴,,,
∴,
∴
∵,
∴,
∴.
在中,由勾股定理得,,
∴,
故选B.
【点睛】本题主要考查了平行四边形的性质,线段垂直平分线的性质,等腰三角形的性质与判定,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
10.A
【详解】延长PF交AB的延长线于点G.如图所示:
在△BGF与△CPF中,
,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=PG,
∵PF=PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP ∠FEP=∠EPC ∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180° ∠A=80°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=(180° 80°)=50°,
∴∠FPC=50°;
故选A.
【点睛】本题考查了菱形的性质、全等三角形的判定与性质、线段垂直平分线上的点到两个端点的距离相等的性质,等边对等角的性质,熟记性质并且作出辅助线求出EF=PF是解题的关键,也是本题的难点.
11.C
【分析】先根据三角形内角和求出,再根据矩形对角线相等且互相平分得到,再结合等边对等角计算即可.
【详解】解:∵,,
∴,
在矩形中,,
∴,
故选C.
【点睛】本题考查了矩形的性质,三角形内角和,等边对等角,解题的关键是利用矩形得到.
12.D
【分析】先求出AF和EF的长,再根据翻折变换的知识得到EF=BF, 进而求出AB的长.
【详解】∵四边形ABCD是正方形,
∴∠A= 90°,AE= 1,∠AFE= 30°
∴EF= 2,AF=,
∵正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,
EF= BF,
BF= 2,
∴AB= AF+ BF=2+,
故选:D.
【点睛】本题主要考查了翻折变换以及正方形的性质,解题的关键是根据翻折变换得到EF=BF,此题难度不大.
13.45
【分析】根据勾股定理可得直角三角形的另一条直角边的长度,然后根据矩形的面积公式求解即可.
【详解】解:根据勾股定理知,图中直角三角形的另一直角边的长度为:,
∴,
故答案为:45.
【点睛】本题主要考查勾股定理,矩形面积,解题的关键在于正确的运用勾股定理求出矩形的长度.
14.20或12
【分析】根据题意分别画出图形,边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
【详解】解:如图1所示:
在平行四边形中,边上的高为4,,
, ,
,
,
的周长等于
如图2所示:
在中,边上的高为4,,
,
,
的周长等于:,
则的周长等于20或12,
故答案为:20或12.
【点睛】本题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论的方法是解题的关键.
15.5
【分析】作CH∥AB,连接DN,延长DN交CH于H,连接EH,首先证明CH=BD,∠ECH=90°,解直角三角形求出EH,利用三角形中位线定理即可.
【详解】解:作CH∥AB,连接DN并延长交CH于H,连接EH,
∵BD∥CH,∠A=90°,
∴∠B=∠NCH,∠ECH=∠A=90°,
在△DNB和△HNC中,
,
∴△DNB≌△HNC(ASA),
∴CH=BD=8,DN=NH,
∵CH=8,CE=6,
∴,
∵DM=ME,DN=NH,
∴MN=EH=5,
故答案为:5.
【点睛】本题考查全等三角形的判定和性质,三角形的中位线定理,勾股定理,正确添加辅助线、掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
16.5
【分析】先由,AE=求得CE=3,AC=4,再由正方形的性质及勾股定理求得BC=CD=4,进而求得CF=3,最后勾股定理即可求解.
【详解】解:∵,AE=,
∴CE=3,AC=4,
∵四边形ABCD是正方形,
∴AD=CD=BC,,,
∴即,
∴BC=CD=4,
∵EF⊥CD,,
∴,
∴CF=EF,
∵EF⊥CD,
∴即
∴CF=3,
∴.
【点睛】本题主要考查了正方形的性质、勾股定理,熟练掌握勾股定理是解题的关键.
17.(1)2x2﹣x;(2)证明见解析.
【分析】(1)原式利用平方差公式,以及多项式乘以多项式法则计算,合并即可得到结果;
(2)根据三角形的中位线定理和直角三角形斜边中线的性质可得结论.
【详解】(1)解:(2x+1)(2x-1)+(x+1)(1-2x).
=4x2-1+x-2x2+1-2x,
=2x2-x;
(2)证明:∵E,F分别是AD,DC的中点,
∴EF是△ADC的中位线,
∴EF=AC,
∵AB⊥BC,M是AC的中点,
∴BM=AC,
∴EF=BM.
【点睛】本题属于计算和几何的综合题,考查了整式的混合运算,三角形的中位线定理,直角三角形斜边中线的性质等知识,熟练掌握定理和性质是关键.
18.阳光透过的最大面积为平方米
【分析】勾股定理求出的长,进而求出矩形的面积,即可得解.
【详解】解:由图可知:,
∴米,
∴矩形玻璃的面积为:平方米;
∴阳光透过的最大面积为平方米.
【点睛】本题考查勾股定理,矩形的面积.熟练掌握勾股定理,是解题的关键.
19.顶点D的坐标为
【分析】本题考查了正方形的性质,坐标与图形,直角三角形的性质.根据直角三角形的性质得出,,再由正方形的性质得出,,过点D作x轴的垂线,垂足为E,再根据直角三角形的性质得出和的值,据此求解即可.
【详解】解:点A的坐标为,
,
∵,
∴,
∴,
在正方形中,,,
如图,过点D作x轴的垂线,垂足为E,则,
,
,,
,
顶点D的坐标为.
20.(1)①45°②3
(2)
【分析】(1)①等边对等角,得到,即可;
②勾股定理求出,再利用勾股定理求出的长即可;
(2)过点作,延长交于点,证明,得到,设,则:,在中勾股定理求出的值,进而求出的值,利用,求出的长,再利用勾股定理求的长即可.
【详解】(1)解:①∵以为斜边作等腰,
∴,
∴;
故答案为:45°;
②∵边长为4的正方形,,
∴,
∴,
∴;
故答案为:3.
(2)解:过点作于M,延长交于点,则:,
∵,
∴四边形为矩形,
∴,,
∵,
∴,
又,
∴,
∴,
设,则:,
在中,,
∴,解得:或(不合题意,舍去);
∴,
∴,
∴,
∴.
【点睛】本题考查正方形的性质,等腰三角形的性质,矩形的判定和性质,全等三角形的判定和性质,勾股定理.熟练掌握相关性质,添加辅助线构造特殊三角形和全等三角形,是解题的关键.
21.(1)见详解.
(2)13
【分析】本题考查了平行四边形的性质,角平分线的性质,等腰三角形的三线合一性质知识,
(1)根据平行四边形性质和角平分线性质可得,.即可得到,.即可求证结论.
(2)过点A作,垂足为H,利用,可计算出的长度,结合(1)即可求出长度.
【详解】(1)解:∵四边形是平行四边形.
∴,,.
∴,.
∵是的平分线,是的平分线.
∴,.
∴,.
∴,.
∴.
∴.
∴.
(2)过点A作,垂足为H,如图:
由(1)知,且,,
∴, .
∵,
∴,
∴,.
∴.
∵.
∴.
∴.
∴.
22.(1)90°;(2)见解析;(3).
【分析】(1)根据图形和已知的△ABE旋转得到△ADF即可得出答案;
(2)由旋转的性质可得∠F=∠AEB,由余角的性质可得结论;
(3)由勾股定理可求BE的长,再由△DGE∽△BAE可求GE的长.
【详解】(1)旋转中心是点A,旋转角度是90°;
(2)∵△ADF是由△ABE旋转得到,
∴△ADF≌△ABE,
∴∠F=∠AEB,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AEB+∠ABE=90°,
∴∠F+∠ABE=90°,
∴∠FGB=90°,
∴BG⊥DF;
(3)∵正方形ABCD的边长是4,
∴AB=4,
∴在Rt△ABE中,BE==5,
∵AE=3,
∴DE=AD-AE=1.
∵∠DGE=∠BAE=90°,∠DEG=∠BEA,
∴△DGE∽△BAE,
∴
∴GE=
【点睛】本题综合考查了正方形的旋转,旋转的性质,勾股定理,三角形的内角和定理,全等三角形的性质和判定等知识点,主要考查学生能根据旋转得出全等三角形,进一步推出角相等,同时考查学生观察图形的能力、猜想的能力.
23.(1)详见解析;(2)OG=BF;(3)正方形ABCD的面积=2
【分析】(1)根据全等三角形的判定方法中SAS即可证得△BCE≌△DCF.
(2)因为O是BD的中点,结合已知条件,证明G是DF中点,利用中位线定理即可解题.
(3)要求正方形的面积,求出边长的平方即可,根据正方形的性质,可将BC·BD用x表示出来,即可求解.
【详解】(1)证明:在△BCE与△DCF中,
∵BC=DC,∠BCE=∠DCF=90°,CE=CF,
∴△BCE≌△DCF.
(2)OG=BF.
理由如下:∵△BCE≌△DCF,
∴∠CEB=∠F,
∵∠CEB=∠DEG,
∴∠F=∠DEG,
∵∠F+∠GDE=90°,
∴∠DEG+∠GDE=90°,
∴BG⊥DF,
∴∠BGD=∠BGF,
又∵BG=BG,∠DBG=∠FBG,
∴△BGD≌△BGF,
∴DG=GF,
即G为DF中点
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG=BF.
(3)设BC=x,则DC=x,BD=x,
∵BC·BD=2
即x·x=2
解得x2=2
即:正方形ABCD的面积是2.
【点睛】本题综合考查了全等三角形的判定与性质、正方形的性质、中位线,灵活运用即可解题.
24.(1)相等,理由见详解
(2)是中点时,四边形是矩形,理由见详解
(3)时,四边形为正方形,理由见详解
【分析】(1)由平分,平分,可得,,再根据,可得,,即有,,则有,,问题得解;
(2)证明,且、互相平分,即可判断四边形是矩形,据此作答即可;
(3)根据对角线相互垂直的矩形是正方形作答即可.
【详解】(1),理由如下:
∵根据题意,有平分,平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴;
(2)是中点时,四边形是矩形,理由如下:
在(1)已证明,
∵是中点,
∴,
∴,
∴,且、互相平分,
∴四边形是矩形;
(3)当时,四边形为正方形,理由如下:
在(2)中已证明四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴矩形是正方形.
【点睛】本题主要考查了平行线的性质,角平分线的定义,矩形的判定,正方形的判定等知识,掌握平行线的性质是解答本题的关键.
25.(1)是等腰三角形,理由见解析
(2)
(3)万元
【分析】(1)利用平行四边形的性质求出,进而可得,则是等腰三角形;
(2)根据已知条件可得,从而的值转化为求的值即可;
(3)如图所示,过点M作,过点A作交于P,则四边形是平行四边形,,同理可得,求出,进而推出当三点共线时,最小,即最小,最小值为,由勾股定理得,则,据此求解即可.
【详解】(1)解:是等腰三角形,理由如下:
∵四边形是平行四边形,,
∴,
∴,
∴是等腰三角形;
(2)解:连接、,如图:
在中,,
,
,
,,,
,
,
过点作于点,
,
,
,
;
.
种植马鞭草区域的面积为.
(3)解:如图所示,过点M作,过点A作交于P,则四边形是平行四边形,
∴,
同理可得,
∵,
∴,
∴,
∴,
∴,
∴当三点共线时,最小,即最小,最小值为,
在中,由勾股定理得,
∴,
∴修建这三条绿道投入资金的最小值为万元.
第十八章 平行四边形
(本试卷三个大题,25个小题。满分150分,考试时间120分钟。)
姓名 班级 学号 成绩
一、选择题(本题共12个小题,每小题3分,共36分;每个小题只有一项符合题意。)
1.菱形ABCD的对角线AC=6,BD=8,那么边AB的长度 是( )
A.10 B.5 C. D.
2.在平行四边形中,若,则( )
A. B. C. D.
3.将一张边长分别为8、6的矩形纸片ABCD折叠,使点C与A重合,则折痕的长为( )
A.6 B.6.5 C.7.5 D.10
4.下列说法中错误的是( )
A.直角三角形斜边上的中线等于斜边的一半
B.等底等高三角形的面积相等
C.三角形的中位线平行于第三边,并且等于第三边的一半
D.如果三角形两条边的长分别是a、b,第三边长为c,则有a2+b2=c2
5.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )
A.6cm B.5cm C. D.
6.如图,在菱形中,,则的度数为( )
A.
B.
C.
D.
7.如图,的对角线、交于,则下列结论一定成立的是( )
A. B. C. D.
8.如图,点在正方形的边上,若,,那么正方形的面积为( )
A.
B.
C.
D.
9.如图,在中,垂直平分于点E,,,则的对角线的长为( )
A. B. C. D.
10.如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.50° B.55° C.60° D.45°
11.如图,在矩形中,,交于点,于点,若,则的度数为( )
A. B. C. D.
12.如图,将正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,折痕交AB于点F,交CD于点G.若,,则AB的长为( )
A.2 B. C. D.
二、填空题(本题共4个小题,每小题4分,共16分。)
13.如右图,带阴影的矩形面积是 .
14.在平行四边形中,,,边上的高为4,则平行四边形周长等于 .
15.如右图,在中,,,点D,E分别在边AB,AC上,且,,连接DE,点M是DE的中点,点N是BC的中点,则线段MN的长为 .
16.在正方形ABCD中,点E在对角线AC上,作EF⊥CD于点F,连接BF,当,AE=时,则BF= .
三、解答题(本题共9个小题,共98分。)
17.(10分) (1)化简:(2x+1)(2x﹣1)+(x+1)(1﹣2x). (5分)
(2)如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证:EF=BM. (5分)
18.(8分) 如图,小明准备建一个鲜花大棚,棚宽米,高米,长米,棚的斜面用矩形玻璃遮盖,不计墙的厚度,请计算阳光透过的最大面积.
19.(10分) 如图,在平面直角坐标系中,正方形的顶点A,B分别在轴,轴的正半轴上,顶点的坐标为,,求顶点的坐标.
20.(12分)如图,在边长为4的正方形中,点是边上一点,,连结,以为斜边作等腰,点在正方形内,连接;
(1)①_________;(4分)
②_________;(4分)
(2)求的长.(4分)
21.(10分)如图,平行四边形中,的平分线交于E,的平分线交于点F.
(1)求证:;(5分)
(2)若,,,求的长.(5分)
22.(12分)如图,边长为4的正方形ABCD中,点E在AD上,△ABE逆时针旋转一定角度后得到△ADF,延长BE交DF于点G,若AE=3.
(1)指出旋转中心和旋转角度;(4分)
(2)求证:BG⊥DF;(4分)
(3)求线段GE的长.(4分)
23.(12分) 已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
(1)说明:△BCE≌△DCF;
(2)OG与BF有什么数量关系?说明你的结论;(6分)
(3)若BC·BD=,求正方形ABCD的面积.(6分)
24.(12分) 如图,在中,点是边上的一个动点(点不与、两点重合),过点作直线,直线与的平分线相交于点,与(的外角)的平分线相交于点.
(1)与相等吗?为什么?(4分)
(2)探究:当点运动到何处时,四边形是矩形?并证明你的结论.(4分)
(3)在(2)中当等于多少时,四边形为正方形(不要求说理由)(4分)
25.(12分)如图1所示,平行四边形是苏州乐园某主题区域的平面示意图,A,B,C,D分别是该区域的四个入口,两条主干道,交于点O,请你帮助苏州乐园的管理人员解决以下问题:
(1)若,你能判断的形状吗?请说明理由.(4分)
(2)在(1)的条件下,如图2,乐园管理人员为提升游客游览的体验感,准备修建三条绿道,其中点M在上,点N在上,且(点M与点O,B不重合),并计划在与两块绿地所在区域种植花期长久的马鞭草,求种植马鞭草区域的面积.(4分)
中小学教育资源及组卷应用平台
(3)若将该区域扩大,如图3,此时,修建(2)中的绿道每千米费用为4万元,请你计算修建这三条绿道投入资金的最小值.(4分)21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长.
【详解】解:根据题意,设对角线AC、BD相较于O,
∵四边形ABCD是菱形.
∴AO=AC=3,BO=BD=4,且AO⊥BO,
∴AB=5,
故选B.
【点睛】本题考查菱形的性质,要熟练掌握菱形对角线的性质,及勾股定理的灵活运用.
2.B
【分析】根据平行四边形的性质,即可求解.
【详解】解:∵四边形是平行四边形,
∴.
故选B.
【点睛】本题主要考查了平行四边形的性质,熟练掌握平行四边形的对角相等是解题的关键.
3.C
【详解】如图,设折痕为EF,由题意可知:EF垂直平分AC,作EM⊥BC于M,
∴CE=AE,
设DE为x,则CE=AE=8-x,在Rt△CDE中,由勾股定理可得:,
解得:,
∴DE=CM=,
同理可得:BF=,
∴MF=BC-BF-CM=,
在Rt△EFM中,由勾股定理可得:.
故选C.
点睛:在有关矩形的折叠问题中,需注意两个问题:(1)折叠前后的两个对应图形是关于折痕对称的,要充分利用轴对称的性质;(2)把已知量和要求的量集中到一个直角三角形中,利用勾股定理建立方程来解题.
4.D
【分析】根据三角性有关的性质可逐一分析选项,即可得到答案.
【详解】A项正确,直角三角形斜边上的中线等于斜边的一半;B项正确,等底等高三角形的面积相等;C项正确,三角形的中位线平行于第三边,并且等于第三边的一半;D项错误如果三角形两条边的长分别是a、b,第三边长为c,则不一定是a2+b2=c2,有可能不是直角三角形.
【点睛】本题考查了三角形的的性质、三角形的面积及勾股定理相关的知识,学生针对此题需要认真掌握相关定理,即可求解.
5.B
【详解】∵菱形的两条对角线分别为5cm和10cm,
∴菱形的面积为:(cm2),
设正方形的边长为cm,则,解得:(cm).
故选B.
6.B
【分析】根据菱形的对角线平分一组对角,菱形的邻角互补求解即可.
【详解】解:∵在菱形中,,
∴,
∴,
故选:B.
【点睛】本题考查了菱形的性质,熟知菱形的对角线平分一组对角,菱形的邻角互补是解题的关键.
7.C
【分析】根据平行四边形的性质可直接判断求解.
【详解】解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,AB=CD,
A、OA=OB,不一定成立,故该选项不符合题意;
B、AC=BD,不一定成立,故该选项不符合题意;
C、AB=CD,成立,故该选项符合题意;
D、,不一定成立,故该选项不符合题意;
故选:C.
【点睛】本题主要考查了平行四边形的性质,掌握平行四边形的性质是解题的关键.
8.A
【分析】根据正方形的性质可得,根据勾股定理即可求得,即可求解.
【详解】解:∵四边形是正方形,
∴,
在中,,
∴正方形的面积.
故选:A.
【点睛】本题考查了勾股定理,正方形的性质,熟练掌握正方形的性质和勾股定理是解题的关键.
9.B
【分析】连接交于点F,根据平行四边形和线段垂直平分线的性质可以推出,即可推出,先利用勾股定理求出的长,即可求出的长.
【详解】解:如图,连接交于点F.
∵垂直平分,
∴,
∵四边形为平行四边形,
∴,,,
∴,
∴
∵,
∴,
∴.
在中,由勾股定理得,,
∴,
故选B.
【点睛】本题主要考查了平行四边形的性质,线段垂直平分线的性质,等腰三角形的性质与判定,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
10.A
【详解】延长PF交AB的延长线于点G.如图所示:
在△BGF与△CPF中,
,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=PG,
∵PF=PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP ∠FEP=∠EPC ∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180° ∠A=80°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=(180° 80°)=50°,
∴∠FPC=50°;
故选A.
【点睛】本题考查了菱形的性质、全等三角形的判定与性质、线段垂直平分线上的点到两个端点的距离相等的性质,等边对等角的性质,熟记性质并且作出辅助线求出EF=PF是解题的关键,也是本题的难点.
11.C
【分析】先根据三角形内角和求出,再根据矩形对角线相等且互相平分得到,再结合等边对等角计算即可.
【详解】解:∵,,
∴,
在矩形中,,
∴,
故选C.
【点睛】本题考查了矩形的性质,三角形内角和,等边对等角,解题的关键是利用矩形得到.
12.D
【分析】先求出AF和EF的长,再根据翻折变换的知识得到EF=BF, 进而求出AB的长.
【详解】∵四边形ABCD是正方形,
∴∠A= 90°,AE= 1,∠AFE= 30°
∴EF= 2,AF=,
∵正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,
EF= BF,
BF= 2,
∴AB= AF+ BF=2+,
故选:D.
【点睛】本题主要考查了翻折变换以及正方形的性质,解题的关键是根据翻折变换得到EF=BF,此题难度不大.
13.45
【分析】根据勾股定理可得直角三角形的另一条直角边的长度,然后根据矩形的面积公式求解即可.
【详解】解:根据勾股定理知,图中直角三角形的另一直角边的长度为:,
∴,
故答案为:45.
【点睛】本题主要考查勾股定理,矩形面积,解题的关键在于正确的运用勾股定理求出矩形的长度.
14.20或12
【分析】根据题意分别画出图形,边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
【详解】解:如图1所示:
在平行四边形中,边上的高为4,,
, ,
,
,
的周长等于
如图2所示:
在中,边上的高为4,,
,
,
的周长等于:,
则的周长等于20或12,
故答案为:20或12.
【点睛】本题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论的方法是解题的关键.
15.5
【分析】作CH∥AB,连接DN,延长DN交CH于H,连接EH,首先证明CH=BD,∠ECH=90°,解直角三角形求出EH,利用三角形中位线定理即可.
【详解】解:作CH∥AB,连接DN并延长交CH于H,连接EH,
∵BD∥CH,∠A=90°,
∴∠B=∠NCH,∠ECH=∠A=90°,
在△DNB和△HNC中,
,
∴△DNB≌△HNC(ASA),
∴CH=BD=8,DN=NH,
∵CH=8,CE=6,
∴,
∵DM=ME,DN=NH,
∴MN=EH=5,
故答案为:5.
【点睛】本题考查全等三角形的判定和性质,三角形的中位线定理,勾股定理,正确添加辅助线、掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
16.5
【分析】先由,AE=求得CE=3,AC=4,再由正方形的性质及勾股定理求得BC=CD=4,进而求得CF=3,最后勾股定理即可求解.
【详解】解:∵,AE=,
∴CE=3,AC=4,
∵四边形ABCD是正方形,
∴AD=CD=BC,,,
∴即,
∴BC=CD=4,
∵EF⊥CD,,
∴,
∴CF=EF,
∵EF⊥CD,
∴即
∴CF=3,
∴.
【点睛】本题主要考查了正方形的性质、勾股定理,熟练掌握勾股定理是解题的关键.
17.(1)2x2﹣x;(2)证明见解析.
【分析】(1)原式利用平方差公式,以及多项式乘以多项式法则计算,合并即可得到结果;
(2)根据三角形的中位线定理和直角三角形斜边中线的性质可得结论.
【详解】(1)解:(2x+1)(2x-1)+(x+1)(1-2x).
=4x2-1+x-2x2+1-2x,
=2x2-x;
(2)证明:∵E,F分别是AD,DC的中点,
∴EF是△ADC的中位线,
∴EF=AC,
∵AB⊥BC,M是AC的中点,
∴BM=AC,
∴EF=BM.
【点睛】本题属于计算和几何的综合题,考查了整式的混合运算,三角形的中位线定理,直角三角形斜边中线的性质等知识,熟练掌握定理和性质是关键.
18.阳光透过的最大面积为平方米
【分析】勾股定理求出的长,进而求出矩形的面积,即可得解.
【详解】解:由图可知:,
∴米,
∴矩形玻璃的面积为:平方米;
∴阳光透过的最大面积为平方米.
【点睛】本题考查勾股定理,矩形的面积.熟练掌握勾股定理,是解题的关键.
19.顶点D的坐标为
【分析】本题考查了正方形的性质,坐标与图形,直角三角形的性质.根据直角三角形的性质得出,,再由正方形的性质得出,,过点D作x轴的垂线,垂足为E,再根据直角三角形的性质得出和的值,据此求解即可.
【详解】解:点A的坐标为,
,
∵,
∴,
∴,
在正方形中,,,
如图,过点D作x轴的垂线,垂足为E,则,
,
,,
,
顶点D的坐标为.
20.(1)①45°②3
(2)
【分析】(1)①等边对等角,得到,即可;
②勾股定理求出,再利用勾股定理求出的长即可;
(2)过点作,延长交于点,证明,得到,设,则:,在中勾股定理求出的值,进而求出的值,利用,求出的长,再利用勾股定理求的长即可.
【详解】(1)解:①∵以为斜边作等腰,
∴,
∴;
故答案为:45°;
②∵边长为4的正方形,,
∴,
∴,
∴;
故答案为:3.
(2)解:过点作于M,延长交于点,则:,
∵,
∴四边形为矩形,
∴,,
∵,
∴,
又,
∴,
∴,
设,则:,
在中,,
∴,解得:或(不合题意,舍去);
∴,
∴,
∴,
∴.
【点睛】本题考查正方形的性质,等腰三角形的性质,矩形的判定和性质,全等三角形的判定和性质,勾股定理.熟练掌握相关性质,添加辅助线构造特殊三角形和全等三角形,是解题的关键.
21.(1)见详解.
(2)13
【分析】本题考查了平行四边形的性质,角平分线的性质,等腰三角形的三线合一性质知识,
(1)根据平行四边形性质和角平分线性质可得,.即可得到,.即可求证结论.
(2)过点A作,垂足为H,利用,可计算出的长度,结合(1)即可求出长度.
【详解】(1)解:∵四边形是平行四边形.
∴,,.
∴,.
∵是的平分线,是的平分线.
∴,.
∴,.
∴,.
∴.
∴.
∴.
(2)过点A作,垂足为H,如图:
由(1)知,且,,
∴, .
∵,
∴,
∴,.
∴.
∵.
∴.
∴.
∴.
22.(1)90°;(2)见解析;(3).
【分析】(1)根据图形和已知的△ABE旋转得到△ADF即可得出答案;
(2)由旋转的性质可得∠F=∠AEB,由余角的性质可得结论;
(3)由勾股定理可求BE的长,再由△DGE∽△BAE可求GE的长.
【详解】(1)旋转中心是点A,旋转角度是90°;
(2)∵△ADF是由△ABE旋转得到,
∴△ADF≌△ABE,
∴∠F=∠AEB,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AEB+∠ABE=90°,
∴∠F+∠ABE=90°,
∴∠FGB=90°,
∴BG⊥DF;
(3)∵正方形ABCD的边长是4,
∴AB=4,
∴在Rt△ABE中,BE==5,
∵AE=3,
∴DE=AD-AE=1.
∵∠DGE=∠BAE=90°,∠DEG=∠BEA,
∴△DGE∽△BAE,
∴
∴GE=
【点睛】本题综合考查了正方形的旋转,旋转的性质,勾股定理,三角形的内角和定理,全等三角形的性质和判定等知识点,主要考查学生能根据旋转得出全等三角形,进一步推出角相等,同时考查学生观察图形的能力、猜想的能力.
23.(1)详见解析;(2)OG=BF;(3)正方形ABCD的面积=2
【分析】(1)根据全等三角形的判定方法中SAS即可证得△BCE≌△DCF.
(2)因为O是BD的中点,结合已知条件,证明G是DF中点,利用中位线定理即可解题.
(3)要求正方形的面积,求出边长的平方即可,根据正方形的性质,可将BC·BD用x表示出来,即可求解.
【详解】(1)证明:在△BCE与△DCF中,
∵BC=DC,∠BCE=∠DCF=90°,CE=CF,
∴△BCE≌△DCF.
(2)OG=BF.
理由如下:∵△BCE≌△DCF,
∴∠CEB=∠F,
∵∠CEB=∠DEG,
∴∠F=∠DEG,
∵∠F+∠GDE=90°,
∴∠DEG+∠GDE=90°,
∴BG⊥DF,
∴∠BGD=∠BGF,
又∵BG=BG,∠DBG=∠FBG,
∴△BGD≌△BGF,
∴DG=GF,
即G为DF中点
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG=BF.
(3)设BC=x,则DC=x,BD=x,
∵BC·BD=2
即x·x=2
解得x2=2
即:正方形ABCD的面积是2.
【点睛】本题综合考查了全等三角形的判定与性质、正方形的性质、中位线,灵活运用即可解题.
24.(1)相等,理由见详解
(2)是中点时,四边形是矩形,理由见详解
(3)时,四边形为正方形,理由见详解
【分析】(1)由平分,平分,可得,,再根据,可得,,即有,,则有,,问题得解;
(2)证明,且、互相平分,即可判断四边形是矩形,据此作答即可;
(3)根据对角线相互垂直的矩形是正方形作答即可.
【详解】(1),理由如下:
∵根据题意,有平分,平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴;
(2)是中点时,四边形是矩形,理由如下:
在(1)已证明,
∵是中点,
∴,
∴,
∴,且、互相平分,
∴四边形是矩形;
(3)当时,四边形为正方形,理由如下:
在(2)中已证明四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴矩形是正方形.
【点睛】本题主要考查了平行线的性质,角平分线的定义,矩形的判定,正方形的判定等知识,掌握平行线的性质是解答本题的关键.
25.(1)是等腰三角形,理由见解析
(2)
(3)万元
【分析】(1)利用平行四边形的性质求出,进而可得,则是等腰三角形;
(2)根据已知条件可得,从而的值转化为求的值即可;
(3)如图所示,过点M作,过点A作交于P,则四边形是平行四边形,,同理可得,求出,进而推出当三点共线时,最小,即最小,最小值为,由勾股定理得,则,据此求解即可.
【详解】(1)解:是等腰三角形,理由如下:
∵四边形是平行四边形,,
∴,
∴,
∴是等腰三角形;
(2)解:连接、,如图:
在中,,
,
,
,,,
,
,
过点作于点,
,
,
,
;
.
种植马鞭草区域的面积为.
(3)解:如图所示,过点M作,过点A作交于P,则四边形是平行四边形,
∴,
同理可得,
∵,
∴,
∴,
∴,
∴,
∴当三点共线时,最小,即最小,最小值为,
在中,由勾股定理得,
∴,
∴修建这三条绿道投入资金的最小值为万元.
