【七下专项突破讲练】专题11.2 不等式及其性质(分层练习)(含解析)
文档属性
| 名称 | 【七下专项突破讲练】专题11.2 不等式及其性质(分层练习)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 758.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 09:39:39 | ||
图片预览




文档简介
专题11.2 不等式及其性质(分层练习)
单选题
1.(22-23八年级下·云南文山·阶段练习)在下列式子:①;②;③;④;⑤中,是不等式的有( )
A.1个 B.2个 C.3个 D.4个
2.(22-23七年级下·河南洛阳·阶段练习)语句“的一半与的2倍的差是非负数”可以表示为( )
A. B. C. D.
3.(20-21七年级下·河南周口·期中)下列关系式中不含这个解的是( )
A. B.
C. D.
4.(23-24八年级下·陕西西安·阶段练习)若,则下列不等式中正确的是( )
A. B.
C. D.
5.(19-20六年级下·全国·课时练习)已知,则不等式组的解集是( )
A. B. C. D.无解
6.(2022·安徽马鞍山·二模)若,则下列各式中正确的是( )
A. B. C. D.
7.(2023·浙江杭州·二模) 次生活常识竞赛共有20题,答对一题得5分,不答得0分,答错一题扣2分.小滨有1题没答,竞赛成绩不低于80分,设小聪答错了x题,则( )
A. B. C. D.
8.(2023·安徽·模拟预测)已知实数满足,则下列结论不正确的是( )
A. B. C. D.
9.(2023·浙江杭州·二模)若,,则下列不等式中一定成立的是( )
A. B. C. D.
10.(23-24八年级上·湖北武汉·阶段练习)如图,在中,,为(不含端点)上一点,则可能是( )
A. B. C. D.
填空题
11.(2024八年级下·全国·专题练习)或的否定形式为 .
12.(19-20八年级上·湖北武汉·期中)若三角形三边长分别为2、a、5,则a的取值范围为 .
13.(23-24八年级下·陕西西安·开学考试)若,则 .
14.(23-24七年级上·江苏盐城·阶段练习)若,则 .
15.(2024七年级·全国·竞赛)七年级()班在数学知识竞赛中获一等奖的人数占全班人数的,获二等奖的人数占全班人数的,获三等奖的人数占全班人数的,还有不足人未获奖,则七年级()班共有学生 名.
16.(19-20七年级上·江西吉安·期中)已知对,,且,则 .
17.(20-21六年级下·上海杨浦·期末)如果 ,那么
18.(22-23七年级下·全国·课时练习)已知,下列结论:①;②;③若,则;④若,则.其中正确的结论是 (填序号).
19.(20-21八年级上·四川成都·阶段练习)若方程组的解是(m为常数),方程组的解x、y满足,则m的取值范围为 .
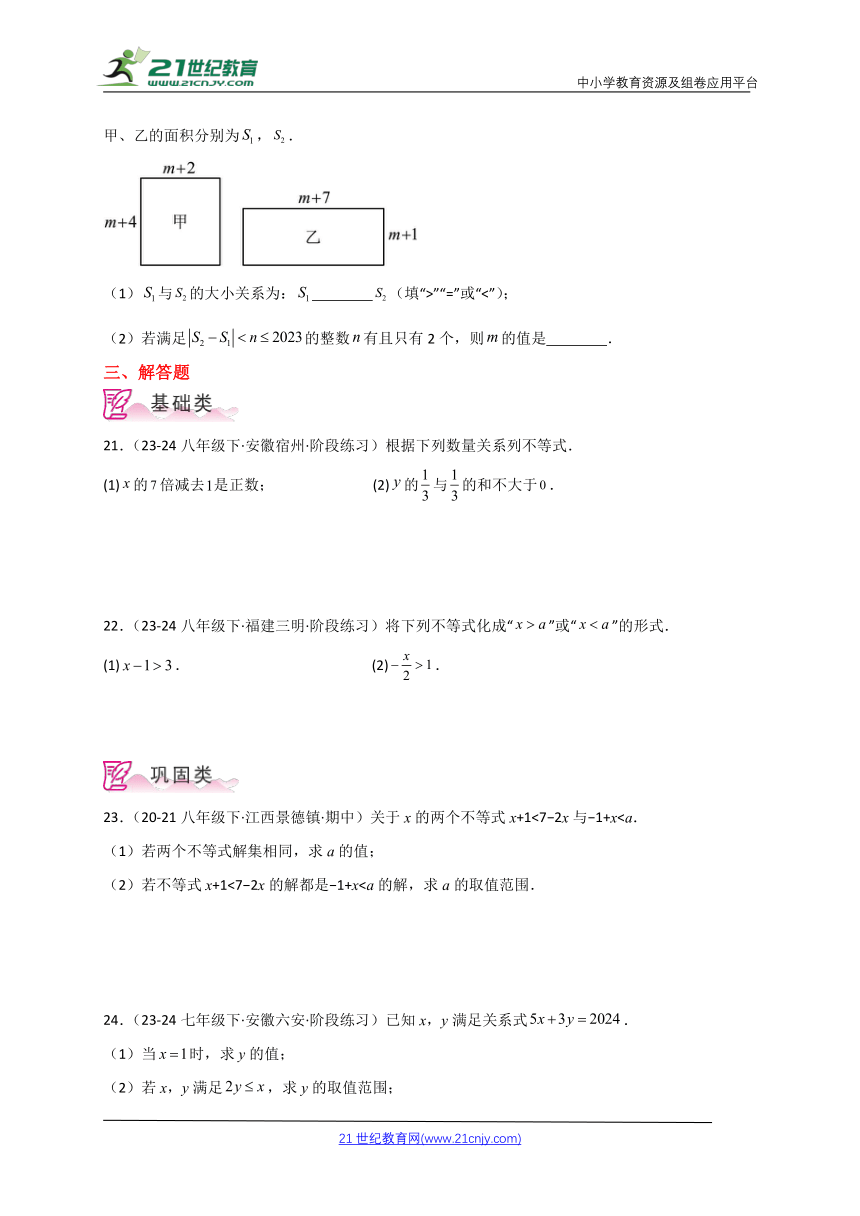
20.(22-23七年级下·安徽滁州·期末)已知甲、乙两个长方形,它们的边长如图所示(为正整数),甲、乙的面积分别为,.
(1)与的大小关系为: (填“>”“=”或“<”);
(2)若满足的整数有且只有2个,则的值是 .
解答题
21.(23-24八年级下·安徽宿州·阶段练习)根据下列数量关系列不等式.
(1)的倍减去是正数; (2)的与的和不大于.
22.(23-24八年级下·福建三明·阶段练习)将下列不等式化成“”或“”的形式.
(1). (2).
23.(20-21八年级下·江西景德镇·期中)关于x的两个不等式x+1<7 2x与 1+x(1)若两个不等式解集相同,求a的值;
(2)若不等式x+1<7 2x的解都是 1+x24.(23-24七年级下·安徽六安·阶段练习)已知x,y满足关系式.
(1)当时,求y的值;
(2)若x,y满足,求y的取值范围;
(3)若x,y满足,且,求a的取值范围.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】本题考查了不等式的定义,用不等号连接的式子是不等式.根据用不等号连接的式子是不等式,可得不等式的个数.
【详解】在下列式子:①;②;③;④;⑤中,
是不等式的有①②⑤,共3个.
故选:C.
2.D
【分析】本题考查列代数式与列不等式,先根据“的一半与的2倍的差”列代数式,再根据“非负数是大于等于0”列不等式即可得答案.熟练掌握“非负数是大于等于0”是解题关键.
【详解】解:∵“的一半与的2倍的差”表示为,
∴“的一半与的2倍的差是非负数”可以表示为,
故选:D.
3.B
【分析】把x=-1代入各个代数式,满足关系式成立时,它就是该关系式的解.
【详解】解:当x=-1时,2x+1=-1,-2x+1=3≥3,-2x-1=1≤3,
所以x=-1满足选项A、C、D,因为-1不大于-1,所以x=-1不满足B.
故选:B.
【点睛】本题考查了等式、不等式的解及解的判断方法.理解“≥”“≤”是关键.
4.B
【分析】本题考查的是不等式的性质,解题的关键是熟练掌握不等式的性质,
根据不等式的基本性质解答即可.
【详解】解:A.由,得,故不符合题意.
B.由,得,推断出,故符合题意.
C.由,得,故不符合题意.
D.由,得,故不符合题意.
故选:B.
5.C
【分析】根据不等式的解集的定义,由m、n的大小关系以及不等式组的式子,得到不等式组的解集.
【详解】解:∵且,x大于小的数,大于大的数,
∴x的解集是.
故选:C.
【点睛】本题考查不等式的解集,解题的关键是掌握求不等式解集的方法.
6.B
【分析】根据,可以取满足条件的特殊值,进行判断.
【详解】解:,当,时,
A、,,,故该选项错误,不符合题意;
B、∵m>n,
∴,
又∵,
∴,故该选项正确,符合题意;
C、,,,故该选项错误,不符合题意;
D、,,,故该选项错误,不符合题意.
故选B.
【点睛】本题考查了不等式,可以采用特殊值的方法进行判断.
7.B
【分析】小聪答错了道题,则答对了道题,根据总分答对题目数答错题目数结合、总分超过80分,即可得出关于的一元一次不等式整理即可得出结论.
【详解】解:设小聪答错了x道题,则答对了道题,
依题意得:,
即:
故选B.
【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
8.C
【分析】本题考查了不等式的性质.根据不等式的性质进行计算和推理,即可求解.
【详解】解:∵,
∴,
∴,A项正确,不符合题意;
由,得,
∴,B项正确,不符合题意;
由,得,
代入,得,
∴,
∵,
∴,,
∴,C项错误,符合题意;
∵,
∴,,,
∴,D项正确,不符合题意;
故选:C.
9.C
【分析】本题考查不等式的性质,根据不等式的基本性质进行判断即可.
【详解】A选项:已知,,当时,,故A选项的不等式不一定成立;
B选项:若,,此时,但,故B选项的不等式不一定成立;
C选项:∵,,
∴,,
∴.
故C选项的不等式一定成立;
D选项:若,,,则,故D选项的不等式不一定成立.
故选:C
10.C
【分析】根据,,得,由,进而可判断求解;
【详解】解:∵,,
∴,
∴,
∴,
又∵,
∴,
∴,
∴x的可能范围为:.
故选:C.
【点睛】本题主要考查三角形外角的性质,不等式的应用,正确列出不等式是解题的关键.
11.或/或
【分析】此题考查了不等式,根据不等式的意义进行解答即可.
【详解】解:或的否定形式是或.
故答案为:或
12.3<a<7
【分析】根据三角形的三边关系求出a的取值范围即可.
【详解】∵三角形的三边长分别为2、a、5,
∴5﹣2<a<5+2,即3<a<7,
故答案为:3<a<7.
【点睛】本题是对三角形三边关系的考查,熟练掌握三角形的三边关系是解决本题的关键.
13.
【分析】
本题考查不等式的性质,根据不等式的性质,进行判断即可.
【详解】
解:两边都乘以,得
,
两边都加,得
,
故答案为:.
14.
【详解】本题考查了不等式的性质与绝对值的意义,解题的关键是熟知:①在不等式的两边同时乘以一个负数,不等号的方向改变;②正数的绝对值是其本身.
根据不等式的性质与绝对值的意义进行变形与化简即可.
解:∵,
∴,
∴.
故答案为:.
15.
【分析】此题考查了一元一次不等式,设全班共有人,则,再根据必须是、和的公倍数即可求解,解题的关键是根据题意,列出不等式.
【详解】解:设全班共有人,
根据题意有,
解得,
因为必须是、和的公倍数,而、和的公倍数中小于的只有,
故答案为:.
16.-1或7或-7.
【分析】由,得到,再结合求出x、y的值,代入计算即可.
【详解】解:∵,,
∴,
∵,
∴,
∴,,,
-1或7或-7.
故答案是:-1或7或-7.
【点睛】本题考查了绝对值的计算和不等式的知识,掌握绝对值的性质是关键.
17.
【分析】利用不等式的性质,不等式的性质是:不等式的两边都加(或减)同一个数或式子,不等号的方向不变;不等式的性质是:不等式的两边都乘(或除以)同一个正数,不等号的方向不变;不等式的性质是:不等式的两边都乘(或除以)同一个负数,不等号的方向改变,进行解答即可.
【详解】解:,
,
,
故答案为:.
【点睛】本题考查了不等式的性质,能熟记不等式的性质的内容是解此题的关键,注意不等式的性质是:不等式的两边都加(或减)同一个数或式子,不等号的方向不变,不等式的性质是:不等式的两边都乘(或除以)同一个正数,不等号的方向不变,不等式的性质是:不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
18.④
【解析】略
19.
【分析】先将转化为与已知的方程组联合起来代数求出和的值即可.
【详解】方程组,
可转换为,
∵方程组的解集为,
∴方程组的解为:,
由②-①得:,,
把代入①得:,
∴,
∴,
故答案为:m>2.
【点睛】本题主要考查了解二元一次方程组,解不等式,熟知解二元一次方程组的加减消元法和代入法是解题的关键.
20. 1011
【分析】(1)先分别计算出面积,作差与0比较大小即可;
(2)先计算出,根据整数n有且只有2个,列出不等式,根据m为正整数即可求值.
【详解】解:(1)∵,,
,
∵m为正整数,
,
,
;
故答案为:;
(2),的整数n有且只有2个,
∴这2个整数解为2023,2022,
,
解得,
.
故答案为:.
【点睛】本题考查了多项式乘多项式法则、绝对值的性质和不等式的性质,能够作差比较是解题的关键.
21.(1);
(2).
【分析】()根据题意,列出不等式即可;
()根据题意,列出不等式即可;
本题考查了列不等式,读懂题意,找到不等量关系是解题的关键.
【详解】(1)解:由题意得:;
(2)解:由题意得:.
22.(1)
(2)
【分析】
本题考查了解不等式,不等式的性质,当不等式两边同时乘上或除以负数,不等式变号,即可作答.
(1)两边都加1,即可作答.
(2)不等式两边同时乘上,即可作答.
【详解】(1)解:根据不等式的基本性质1,两边都加1,得,即.
(2)解:根据不等式的基本性质3,两边都乘,得.
23.(1)a=1;
(2)a≥1.
【分析】(1)求出第二个不等式的解集,表示出第一个不等式的解集,由解集相同求出a的值即可;
(2)根据不等式x+1<7 2x的解都是 1+x【详解】(1)解:由x+1<7 2x得:x<2,
由 1+x由两个不等式的解集相同,得到a+1=2,
解得:a=1;
(2)解:由不等式x+1<7 2x的解都是 1+x得到2≤a+1,
解得:a≥1.
【点睛】此题考查了不等式的解集,根据题意分别求出对应的值,利用不等关系求解.
24.(1)
(2)y的取值范围是
(3)的取值范围是
【分析】
本题考查二元一次方程和不等式的性质,熟练掌握二元一次方程的解法和不等式的基本性质是解题的关键.
(1)把代入,求解即可;
(2)由得,根据,求解即可;
(3)联立和,求解出x,y的值,根据,求解a即可.
【详解】(1)解:把代入,得,
解得;
(2)解:由得,
,
,
,
即y的取值范围是;
(3)解:联立和,
得:
解得,,
,
,
解得,
的取值范围是.
单选题
1.(22-23八年级下·云南文山·阶段练习)在下列式子:①;②;③;④;⑤中,是不等式的有( )
A.1个 B.2个 C.3个 D.4个
2.(22-23七年级下·河南洛阳·阶段练习)语句“的一半与的2倍的差是非负数”可以表示为( )
A. B. C. D.
3.(20-21七年级下·河南周口·期中)下列关系式中不含这个解的是( )
A. B.
C. D.
4.(23-24八年级下·陕西西安·阶段练习)若,则下列不等式中正确的是( )
A. B.
C. D.
5.(19-20六年级下·全国·课时练习)已知,则不等式组的解集是( )
A. B. C. D.无解
6.(2022·安徽马鞍山·二模)若,则下列各式中正确的是( )
A. B. C. D.
7.(2023·浙江杭州·二模) 次生活常识竞赛共有20题,答对一题得5分,不答得0分,答错一题扣2分.小滨有1题没答,竞赛成绩不低于80分,设小聪答错了x题,则( )
A. B. C. D.
8.(2023·安徽·模拟预测)已知实数满足,则下列结论不正确的是( )
A. B. C. D.
9.(2023·浙江杭州·二模)若,,则下列不等式中一定成立的是( )
A. B. C. D.
10.(23-24八年级上·湖北武汉·阶段练习)如图,在中,,为(不含端点)上一点,则可能是( )
A. B. C. D.
填空题
11.(2024八年级下·全国·专题练习)或的否定形式为 .
12.(19-20八年级上·湖北武汉·期中)若三角形三边长分别为2、a、5,则a的取值范围为 .
13.(23-24八年级下·陕西西安·开学考试)若,则 .
14.(23-24七年级上·江苏盐城·阶段练习)若,则 .
15.(2024七年级·全国·竞赛)七年级()班在数学知识竞赛中获一等奖的人数占全班人数的,获二等奖的人数占全班人数的,获三等奖的人数占全班人数的,还有不足人未获奖,则七年级()班共有学生 名.
16.(19-20七年级上·江西吉安·期中)已知对,,且,则 .
17.(20-21六年级下·上海杨浦·期末)如果 ,那么
18.(22-23七年级下·全国·课时练习)已知,下列结论:①;②;③若,则;④若,则.其中正确的结论是 (填序号).
19.(20-21八年级上·四川成都·阶段练习)若方程组的解是(m为常数),方程组的解x、y满足,则m的取值范围为 .
20.(22-23七年级下·安徽滁州·期末)已知甲、乙两个长方形,它们的边长如图所示(为正整数),甲、乙的面积分别为,.
(1)与的大小关系为: (填“>”“=”或“<”);
(2)若满足的整数有且只有2个,则的值是 .
解答题
21.(23-24八年级下·安徽宿州·阶段练习)根据下列数量关系列不等式.
(1)的倍减去是正数; (2)的与的和不大于.
22.(23-24八年级下·福建三明·阶段练习)将下列不等式化成“”或“”的形式.
(1). (2).
23.(20-21八年级下·江西景德镇·期中)关于x的两个不等式x+1<7 2x与 1+x
(2)若不等式x+1<7 2x的解都是 1+x
(1)当时,求y的值;
(2)若x,y满足,求y的取值范围;
(3)若x,y满足,且,求a的取值范围.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】本题考查了不等式的定义,用不等号连接的式子是不等式.根据用不等号连接的式子是不等式,可得不等式的个数.
【详解】在下列式子:①;②;③;④;⑤中,
是不等式的有①②⑤,共3个.
故选:C.
2.D
【分析】本题考查列代数式与列不等式,先根据“的一半与的2倍的差”列代数式,再根据“非负数是大于等于0”列不等式即可得答案.熟练掌握“非负数是大于等于0”是解题关键.
【详解】解:∵“的一半与的2倍的差”表示为,
∴“的一半与的2倍的差是非负数”可以表示为,
故选:D.
3.B
【分析】把x=-1代入各个代数式,满足关系式成立时,它就是该关系式的解.
【详解】解:当x=-1时,2x+1=-1,-2x+1=3≥3,-2x-1=1≤3,
所以x=-1满足选项A、C、D,因为-1不大于-1,所以x=-1不满足B.
故选:B.
【点睛】本题考查了等式、不等式的解及解的判断方法.理解“≥”“≤”是关键.
4.B
【分析】本题考查的是不等式的性质,解题的关键是熟练掌握不等式的性质,
根据不等式的基本性质解答即可.
【详解】解:A.由,得,故不符合题意.
B.由,得,推断出,故符合题意.
C.由,得,故不符合题意.
D.由,得,故不符合题意.
故选:B.
5.C
【分析】根据不等式的解集的定义,由m、n的大小关系以及不等式组的式子,得到不等式组的解集.
【详解】解:∵且,x大于小的数,大于大的数,
∴x的解集是.
故选:C.
【点睛】本题考查不等式的解集,解题的关键是掌握求不等式解集的方法.
6.B
【分析】根据,可以取满足条件的特殊值,进行判断.
【详解】解:,当,时,
A、,,,故该选项错误,不符合题意;
B、∵m>n,
∴,
又∵,
∴,故该选项正确,符合题意;
C、,,,故该选项错误,不符合题意;
D、,,,故该选项错误,不符合题意.
故选B.
【点睛】本题考查了不等式,可以采用特殊值的方法进行判断.
7.B
【分析】小聪答错了道题,则答对了道题,根据总分答对题目数答错题目数结合、总分超过80分,即可得出关于的一元一次不等式整理即可得出结论.
【详解】解:设小聪答错了x道题,则答对了道题,
依题意得:,
即:
故选B.
【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
8.C
【分析】本题考查了不等式的性质.根据不等式的性质进行计算和推理,即可求解.
【详解】解:∵,
∴,
∴,A项正确,不符合题意;
由,得,
∴,B项正确,不符合题意;
由,得,
代入,得,
∴,
∵,
∴,,
∴,C项错误,符合题意;
∵,
∴,,,
∴,D项正确,不符合题意;
故选:C.
9.C
【分析】本题考查不等式的性质,根据不等式的基本性质进行判断即可.
【详解】A选项:已知,,当时,,故A选项的不等式不一定成立;
B选项:若,,此时,但,故B选项的不等式不一定成立;
C选项:∵,,
∴,,
∴.
故C选项的不等式一定成立;
D选项:若,,,则,故D选项的不等式不一定成立.
故选:C
10.C
【分析】根据,,得,由,进而可判断求解;
【详解】解:∵,,
∴,
∴,
∴,
又∵,
∴,
∴,
∴x的可能范围为:.
故选:C.
【点睛】本题主要考查三角形外角的性质,不等式的应用,正确列出不等式是解题的关键.
11.或/或
【分析】此题考查了不等式,根据不等式的意义进行解答即可.
【详解】解:或的否定形式是或.
故答案为:或
12.3<a<7
【分析】根据三角形的三边关系求出a的取值范围即可.
【详解】∵三角形的三边长分别为2、a、5,
∴5﹣2<a<5+2,即3<a<7,
故答案为:3<a<7.
【点睛】本题是对三角形三边关系的考查,熟练掌握三角形的三边关系是解决本题的关键.
13.
【分析】
本题考查不等式的性质,根据不等式的性质,进行判断即可.
【详解】
解:两边都乘以,得
,
两边都加,得
,
故答案为:.
14.
【详解】本题考查了不等式的性质与绝对值的意义,解题的关键是熟知:①在不等式的两边同时乘以一个负数,不等号的方向改变;②正数的绝对值是其本身.
根据不等式的性质与绝对值的意义进行变形与化简即可.
解:∵,
∴,
∴.
故答案为:.
15.
【分析】此题考查了一元一次不等式,设全班共有人,则,再根据必须是、和的公倍数即可求解,解题的关键是根据题意,列出不等式.
【详解】解:设全班共有人,
根据题意有,
解得,
因为必须是、和的公倍数,而、和的公倍数中小于的只有,
故答案为:.
16.-1或7或-7.
【分析】由,得到,再结合求出x、y的值,代入计算即可.
【详解】解:∵,,
∴,
∵,
∴,
∴,,,
-1或7或-7.
故答案是:-1或7或-7.
【点睛】本题考查了绝对值的计算和不等式的知识,掌握绝对值的性质是关键.
17.
【分析】利用不等式的性质,不等式的性质是:不等式的两边都加(或减)同一个数或式子,不等号的方向不变;不等式的性质是:不等式的两边都乘(或除以)同一个正数,不等号的方向不变;不等式的性质是:不等式的两边都乘(或除以)同一个负数,不等号的方向改变,进行解答即可.
【详解】解:,
,
,
故答案为:.
【点睛】本题考查了不等式的性质,能熟记不等式的性质的内容是解此题的关键,注意不等式的性质是:不等式的两边都加(或减)同一个数或式子,不等号的方向不变,不等式的性质是:不等式的两边都乘(或除以)同一个正数,不等号的方向不变,不等式的性质是:不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
18.④
【解析】略
19.
【分析】先将转化为与已知的方程组联合起来代数求出和的值即可.
【详解】方程组,
可转换为,
∵方程组的解集为,
∴方程组的解为:,
由②-①得:,,
把代入①得:,
∴,
∴,
故答案为:m>2.
【点睛】本题主要考查了解二元一次方程组,解不等式,熟知解二元一次方程组的加减消元法和代入法是解题的关键.
20. 1011
【分析】(1)先分别计算出面积,作差与0比较大小即可;
(2)先计算出,根据整数n有且只有2个,列出不等式,根据m为正整数即可求值.
【详解】解:(1)∵,,
,
∵m为正整数,
,
,
;
故答案为:;
(2),的整数n有且只有2个,
∴这2个整数解为2023,2022,
,
解得,
.
故答案为:.
【点睛】本题考查了多项式乘多项式法则、绝对值的性质和不等式的性质,能够作差比较是解题的关键.
21.(1);
(2).
【分析】()根据题意,列出不等式即可;
()根据题意,列出不等式即可;
本题考查了列不等式,读懂题意,找到不等量关系是解题的关键.
【详解】(1)解:由题意得:;
(2)解:由题意得:.
22.(1)
(2)
【分析】
本题考查了解不等式,不等式的性质,当不等式两边同时乘上或除以负数,不等式变号,即可作答.
(1)两边都加1,即可作答.
(2)不等式两边同时乘上,即可作答.
【详解】(1)解:根据不等式的基本性质1,两边都加1,得,即.
(2)解:根据不等式的基本性质3,两边都乘,得.
23.(1)a=1;
(2)a≥1.
【分析】(1)求出第二个不等式的解集,表示出第一个不等式的解集,由解集相同求出a的值即可;
(2)根据不等式x+1<7 2x的解都是 1+x
由 1+x
解得:a=1;
(2)解:由不等式x+1<7 2x的解都是 1+x
解得:a≥1.
【点睛】此题考查了不等式的解集,根据题意分别求出对应的值,利用不等关系求解.
24.(1)
(2)y的取值范围是
(3)的取值范围是
【分析】
本题考查二元一次方程和不等式的性质,熟练掌握二元一次方程的解法和不等式的基本性质是解题的关键.
(1)把代入,求解即可;
(2)由得,根据,求解即可;
(3)联立和,求解出x,y的值,根据,求解a即可.
【详解】(1)解:把代入,得,
解得;
(2)解:由得,
,
,
,
即y的取值范围是;
(3)解:联立和,
得:
解得,,
,
,
解得,
的取值范围是.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
