负数 单元练习卷 人教版数学 六年级下册 2(含答案)
文档属性
| 名称 | 负数 单元练习卷 人教版数学 六年级下册 2(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 09:54:32 | ||
图片预览




文档简介
负数 单元练习卷 人教版数学 六年级下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在﹣,﹢2.8,0,,﹣6.2,﹣18中,正数有( ),负数有( )。
2.电梯从5层下降到层,下降了( )层。
3.一列高铁在济南西站上车的乘客是62名,记作﹢62名,下车的乘客是94名,记作( )名,此时高铁上的人数比原来( )。(填多或少)
4.在现有的记录中,1922年9月13日利比亚的埃尔阿奇亚地区当地气温高达零上57.8℃,记作( )℃;1967年,挪威在北极点附近的气温低至零下94.5℃,记作( )℃。
5.一种扶贫产品包装袋上标示着“净重200±5g”,表示这种特产最轻不少于( )g。其中10包中有一包是次品(较轻),用天平称,至少称( )次一定能保证找到次品。
二、判断题
6.正负数可以表示一组相反意义的量。( )
7.所有的负数都比0小。( )
8.气温0℃比﹣7℃温度高一些,比﹢6℃温度低一些。( )
9.把海平面看作“0”,高于海平面10米记作“﹢10米”,低于海平面10米也记作“﹢10米”。( )
10.一种方便面包装质量规定(90±5)克,抽查到一袋重97克,那么这袋方便面合格。( )
三、选择题
11.下面各数中,( )最接近0。
A.﹣3 B.﹣1 C.﹢2 D.5
12.长沙某天的气温是﹣2℃~8℃,最高气温和最低气温相差( )℃。
A.10℃ B.8℃ C.﹣2℃ D.6℃
13.规定10吨记为0吨,11吨记为﹢1吨,则下列说法错误的是( )。
A.8吨记为﹢8吨 B.15吨记为﹢5吨
C.6吨记为﹣4吨 D.20吨记为﹢10吨
14.有一种计分方法,以90分为标准,94分记作﹢4分,某个学生的成绩记作﹣3分,则他的实际成绩是( )分。
A.93 B.87 C.3 D.﹣3
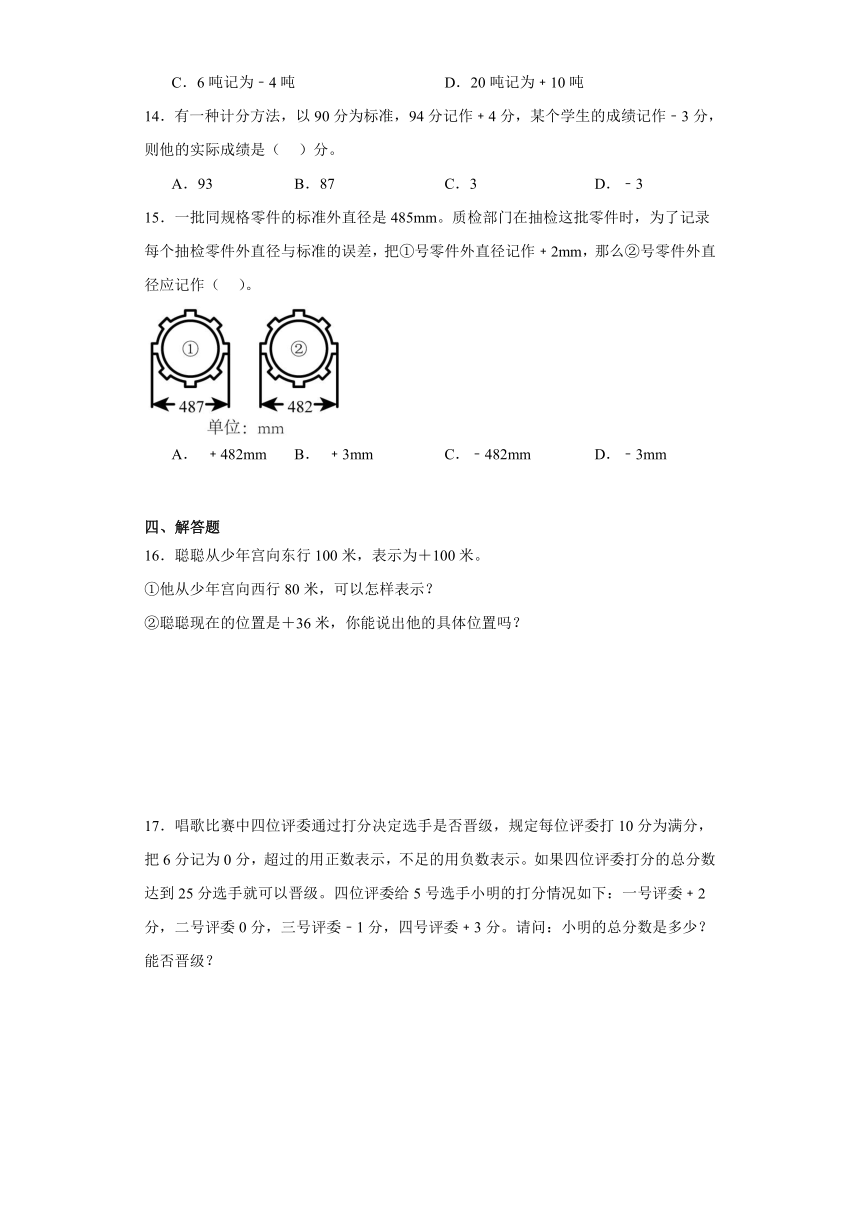
15.一批同规格零件的标准外直径是485mm。质检部门在抽检这批零件时,为了记录每个抽检零件外直径与标准的误差,把①号零件外直径记作﹢2mm,那么②号零件外直径应记作( )。
A. ﹢482mm B. ﹢3mm C.﹣482mm D.﹣3mm
四、解答题
16.聪聪从少年宫向东行100米,表示为+100米。
①他从少年宫向西行80米,可以怎样表示?
②聪聪现在的位置是+36米,你能说出他的具体位置吗?
17.唱歌比赛中四位评委通过打分决定选手是否晋级,规定每位评委打10分为满分,把6分记为0分,超过的用正数表示,不足的用负数表示。如果四位评委打分的总分数达到25分选手就可以晋级。四位评委给5号选手小明的打分情况如下:一号评委﹢2分,二号评委0分,三号评委﹣1分,四号评委﹢3分。请问:小明的总分数是多少?能否晋级?
18.规定向东为正,下图每格表示。
(1)小兰开始在0处,现在在+4处,说明她从0处向( )走了( )。
(2)小乐开始在0处,他向西走了,请你在图中用“△”表示他现在的位置。
(3)淘淘从0处出发,先走,再走。请你在图中用“○”表示出淘淘最后的位置。
19.某工厂规定每人每天要做100个零件,如果某人生产了105个零件,记作:﹢5个;如果某人生产了98个零件,记作:﹣2个。下面是小张一周的生产零件的个数情况:
星期 星期一 星期二 星期三 星期四 星期五
计数/个 ﹣6 ﹢12 ﹢9 ﹣3 ﹢8
(1)从上面的记录中你能看出他在星期几生产的零件个数最多?是多少个?
(2)小张平均每天生产了多少个零件?
20.下表列出了国外几个城市与北京的时差。(带正号的数表示同一时刻比北京时间早的时数)
城市 旧金山 东京 伦敦
与北京的时差/时 ﹣16 ﹢1 ﹣8
(1)如果现在是北京时间11:00,那么伦敦时间和东京时间各是多少?
(2)如果星星在北京时间17:00打电话给远在旧金山的姨妈,你认为合适吗?为什么?
参考答案:
1. ﹢2.8, ﹣,﹣6.2,﹣18
【分析】正数、负数表示两种相反意义的量;正数前面的“﹢”可以省略不写,负数前面的“﹣”不能省略;0既不是正数,也不是负数。
【详解】在﹣,﹢2.8,0,,﹣6.2,﹣18中,
正数有:﹢2.8,;
负数有:﹣,﹣6.2,﹣18。
【点睛】本题考查正负数的认识,注意0既不是正数,也不是负数。
2.6
【分析】电梯没有0层,从5层下降到1层,下降了5-1层,从1层下降到﹣2层,下降了2层,据此分析。
【详解】5-1+2=6(层)
【点睛】关键是理解正负数的意义及实际应用,注意电梯没有0层。
3. ﹣94 少
【分析】用正负数表示意义相反的两种量:上车人数记作正,则下车人数就记作负。由此得解。
【详解】一列高铁在济南西站上车的乘客是62名,记作﹢62名,下车的乘客是94名,记作﹣94名;
62<94
此时高铁上的人数比原来少。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
4. ﹢57.8 ﹣94.5
【分析】正负数可以表示一对具有相反意义的量,这里需要将零度以上记为正,零度以下记为负。
【详解】零上57.8℃,记作﹢57.8℃;零下94.5℃,记作﹣94.5℃。
【点睛】本题考查的是正负数的实际应用,只有具有相反意义的量才可以用正负数来表示。
5. 195 3
【分析】(1)根据正负数的意义“净重200±5g”表示这种产品最多比200g多5g,或者少5g,据此作答即可。
(2)把10个乒乓球分成(5,5)两组放在天平上称,找出上升的一组,再把这5个乒乓球分成(2,2,1)三组,把2个一组的放在天平上称,如平衡,则没称的一个是次品,如不平衡,再把上升的2个乒乓球分成(1,1)放在天平上称,上升的一个就是次品。据此解答。
【详解】这种特产最轻不少于:200-5=195(g)。
第一次称:
把10包产品分成(5,5)两组放在天平上称,找出上升的一组;
第二次称:
把有次品的5包产品分成(2,2,1)三组,把2包一组的放在天平上称,如平衡,则没称的一个是次品;如不平衡,上升的2包产品中有次品;
第三次称:
把上升的2包产品分成(1,1)放在天平上称,上升的一个就是次品;
所以至少称3次就一定能找出次品。
【点睛】本题主要考查了正负数的意义及学生根据天平平衡的原理来解答问题的能力,注意每次取的个数。
6.√
【详解】正负数表示一组相反意义的量;
如:向东记作正,则向西就记作负;
故答案为:√。
7.√
【分析】根据负数的认识,比0小的数叫负数,进行分析。
【详解】所有的负数都比0小,说法正确。
故答案为:√
【点睛】0是正数和负数的分界点,0不是正数也不是负数。
8.√
【分析】根据正负数的定义,比0小的数是负数,比0大的数是正数,据此判断即可。
【详解】由分析可知:
气温0℃比﹣7℃温度高一些,比﹢6℃温度低一些。原题干说法正确。
故答案为:√
【点睛】本题考查正负数,明确正负数的定义是解题的关键。
9.×
【分析】高和低是具有相反意义的量,高于海平面记作“﹢”,那么低于海平面应记作“﹣”,据此解答。
【详解】把海平面看作“0”,高于海平面10米记作“﹢10米”,低于海平面10米应记作“﹣10米”。
故答案为:×
【点睛】掌握正负数的意义和表示方法是解答题目的关键。
10.×
【分析】先确定这种方便面包装质量的合格范围,然后对比,超过范围就不合格,据此判断。
【详解】一种方便面包装质量规定(90±5)克,抽查到一袋重97克,97克>95克,那么这袋方便面不合格,原题说法错误。
故答案为:错误。
【点睛】此题主要考查了正负数的应用。
11.B
【分析】和0的差最小的数,最接近0。据此先求出各个选项中的数和0的差,再选出正确选项即可。
【详解】A.0-(﹣3)=3;
B.0-(﹣1)=1;
C.2-0=2;
D.5-0=5;
3、1、2、5这四个数中1最小,所以﹣1最接近0。
故答案为:B
【点睛】本题考查了正负数,明确正负数的意义是解题的关键。
12.A
【分析】长沙某天的气温是﹣2℃~8℃,则长沙的最低气温是﹣2℃,长沙的最高气温是8℃,则最高气温和最低气温相差10℃。
【详解】8℃与﹣2℃相差10℃。
故答案为:A。
【点睛】本题考查负数,解答本题的关键是掌握负数的概念。
13.A
【分析】根据“规定10吨记为0吨,11吨记为﹢1吨。”可知:以10吨为基准,11吨比10吨多1吨,记作+1吨。即低于10吨的吨数用负数表示,高于10吨的吨数用正数表示。
【详解】A.8吨比10吨少2吨,所以8吨记为-2吨。即8吨记为+8吨是错误的。
B.15吨比10吨多5吨,所以15吨记为+5吨。
C.6吨比10吨少4吨,所以6吨记为-4吨。
D.20吨比10吨多10吨,所以20吨记为+10吨。
故答案为:A
【点睛】用正数和负数表示具有相反意义的量时,要明确“基准”。
14.B
【分析】90分为标准,超过的分数记作正数,不足的分数记作负数,所以﹣3分,就是比标准分少3分。
【详解】根据分析可知90-3=87(分),
故答案为:B
【点睛】正确理解正负数的意义,正负数表示具有相反意义的量。
15.D
【分析】以标准外直径为标准,多于标准外直径记为正,少于标准外直径记为负,据此分析。
【详解】485-482=3(mm),②号零件外直径应记作﹣3mm。
故答案为:D
【点睛】关键是理解正负数的意义,正负数表示意义相反的量。
16.见详解
【分析】向东行为“正”,则向西行为“负”,直接得出结论即可。
【详解】①他从少年宫向西行80米,表示为﹣80米。
②聪聪现在的位置是+36米,说明他在少年宫的东边36米。
【点睛】本题主要考查用正负数来表示具有意义相反的两种量。
17.28分;能晋级
【分析】以6分为标准,高于6分记为正,低于6分记为负,分别求出4个评委打的分数,加起来,与25分比较。
【详解】6+2=8(分)
6-1=5(分)
6+3=9(分)
8+6+5+9
=14+5+9
=19+8
=28(分)
28>25
答:小明的总分数是28分,能晋级。
【点睛】本题考查了正负数的意义和应用,正负数可以表示相反意义的量。
18.(1)东; 40;(2)(3)题如下图。
【分析】根据题意,规定向东为正,则向西为负,据此解答即可。
【详解】(1)规定向东为正,所以﹢4说明向东走了4格,4×10=40(m);
(2)40÷10=4,从0处向西走即向西走4格;
(3)从0处出发,先走,再走,即先向西走2格再向东走7格,最后在0处往东5格处。
(2)(3)作图如下:
【点睛】明确对于具有相反意义的量,规定其中一个量为正,则另一个为负。
19.(1)星期二生产的零件个数最多,是112个;
(2)104个零件
【分析】负数表示比标准数量少,正数表示比标准数量多。据此解答。
【详解】(1)从上面的记录中看出他在星期二生产的零件个数最多,因为+12>+9>+8>﹣3>﹣6; 100+12=112(个);
答:星期二生产的零件个数最多,是112个。
(2)100×5+[(﹣6)+12+9+(﹣3)+8]
=500+20
=520(个)
520÷5=104(个)
答:小张平均每天生产了104个零件。
【点睛】本题考查正负数的应用,明确正负数的意义是解答此题的关键。
20.(1)3:00;12:00
(2)不合适;因为北京时间17:00是旧金山时间的1:00,正处于凌晨。
【分析】(1)正数表示在北京时间向后推几个小时,即加上这个正数,负数表示在北京时间向后前推几个小时,即加上这个负数;
(2)计算出旧金山的时间,然后判断即可。
【详解】(1),即伦敦时间3:00
,即东京时间12:00
(2),即旧金山时间1:00
所以不合适,因为旧金山时间是凌晨1:00,姨妈可能正在休息。
【点睛】此题是典型的正数与负数的实际运用问题,应联系实际生活,认清正数与负数所代表的实际意义。
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在﹣,﹢2.8,0,,﹣6.2,﹣18中,正数有( ),负数有( )。
2.电梯从5层下降到层,下降了( )层。
3.一列高铁在济南西站上车的乘客是62名,记作﹢62名,下车的乘客是94名,记作( )名,此时高铁上的人数比原来( )。(填多或少)
4.在现有的记录中,1922年9月13日利比亚的埃尔阿奇亚地区当地气温高达零上57.8℃,记作( )℃;1967年,挪威在北极点附近的气温低至零下94.5℃,记作( )℃。
5.一种扶贫产品包装袋上标示着“净重200±5g”,表示这种特产最轻不少于( )g。其中10包中有一包是次品(较轻),用天平称,至少称( )次一定能保证找到次品。
二、判断题
6.正负数可以表示一组相反意义的量。( )
7.所有的负数都比0小。( )
8.气温0℃比﹣7℃温度高一些,比﹢6℃温度低一些。( )
9.把海平面看作“0”,高于海平面10米记作“﹢10米”,低于海平面10米也记作“﹢10米”。( )
10.一种方便面包装质量规定(90±5)克,抽查到一袋重97克,那么这袋方便面合格。( )
三、选择题
11.下面各数中,( )最接近0。
A.﹣3 B.﹣1 C.﹢2 D.5
12.长沙某天的气温是﹣2℃~8℃,最高气温和最低气温相差( )℃。
A.10℃ B.8℃ C.﹣2℃ D.6℃
13.规定10吨记为0吨,11吨记为﹢1吨,则下列说法错误的是( )。
A.8吨记为﹢8吨 B.15吨记为﹢5吨
C.6吨记为﹣4吨 D.20吨记为﹢10吨
14.有一种计分方法,以90分为标准,94分记作﹢4分,某个学生的成绩记作﹣3分,则他的实际成绩是( )分。
A.93 B.87 C.3 D.﹣3
15.一批同规格零件的标准外直径是485mm。质检部门在抽检这批零件时,为了记录每个抽检零件外直径与标准的误差,把①号零件外直径记作﹢2mm,那么②号零件外直径应记作( )。
A. ﹢482mm B. ﹢3mm C.﹣482mm D.﹣3mm
四、解答题
16.聪聪从少年宫向东行100米,表示为+100米。
①他从少年宫向西行80米,可以怎样表示?
②聪聪现在的位置是+36米,你能说出他的具体位置吗?
17.唱歌比赛中四位评委通过打分决定选手是否晋级,规定每位评委打10分为满分,把6分记为0分,超过的用正数表示,不足的用负数表示。如果四位评委打分的总分数达到25分选手就可以晋级。四位评委给5号选手小明的打分情况如下:一号评委﹢2分,二号评委0分,三号评委﹣1分,四号评委﹢3分。请问:小明的总分数是多少?能否晋级?
18.规定向东为正,下图每格表示。
(1)小兰开始在0处,现在在+4处,说明她从0处向( )走了( )。
(2)小乐开始在0处,他向西走了,请你在图中用“△”表示他现在的位置。
(3)淘淘从0处出发,先走,再走。请你在图中用“○”表示出淘淘最后的位置。
19.某工厂规定每人每天要做100个零件,如果某人生产了105个零件,记作:﹢5个;如果某人生产了98个零件,记作:﹣2个。下面是小张一周的生产零件的个数情况:
星期 星期一 星期二 星期三 星期四 星期五
计数/个 ﹣6 ﹢12 ﹢9 ﹣3 ﹢8
(1)从上面的记录中你能看出他在星期几生产的零件个数最多?是多少个?
(2)小张平均每天生产了多少个零件?
20.下表列出了国外几个城市与北京的时差。(带正号的数表示同一时刻比北京时间早的时数)
城市 旧金山 东京 伦敦
与北京的时差/时 ﹣16 ﹢1 ﹣8
(1)如果现在是北京时间11:00,那么伦敦时间和东京时间各是多少?
(2)如果星星在北京时间17:00打电话给远在旧金山的姨妈,你认为合适吗?为什么?
参考答案:
1. ﹢2.8, ﹣,﹣6.2,﹣18
【分析】正数、负数表示两种相反意义的量;正数前面的“﹢”可以省略不写,负数前面的“﹣”不能省略;0既不是正数,也不是负数。
【详解】在﹣,﹢2.8,0,,﹣6.2,﹣18中,
正数有:﹢2.8,;
负数有:﹣,﹣6.2,﹣18。
【点睛】本题考查正负数的认识,注意0既不是正数,也不是负数。
2.6
【分析】电梯没有0层,从5层下降到1层,下降了5-1层,从1层下降到﹣2层,下降了2层,据此分析。
【详解】5-1+2=6(层)
【点睛】关键是理解正负数的意义及实际应用,注意电梯没有0层。
3. ﹣94 少
【分析】用正负数表示意义相反的两种量:上车人数记作正,则下车人数就记作负。由此得解。
【详解】一列高铁在济南西站上车的乘客是62名,记作﹢62名,下车的乘客是94名,记作﹣94名;
62<94
此时高铁上的人数比原来少。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
4. ﹢57.8 ﹣94.5
【分析】正负数可以表示一对具有相反意义的量,这里需要将零度以上记为正,零度以下记为负。
【详解】零上57.8℃,记作﹢57.8℃;零下94.5℃,记作﹣94.5℃。
【点睛】本题考查的是正负数的实际应用,只有具有相反意义的量才可以用正负数来表示。
5. 195 3
【分析】(1)根据正负数的意义“净重200±5g”表示这种产品最多比200g多5g,或者少5g,据此作答即可。
(2)把10个乒乓球分成(5,5)两组放在天平上称,找出上升的一组,再把这5个乒乓球分成(2,2,1)三组,把2个一组的放在天平上称,如平衡,则没称的一个是次品,如不平衡,再把上升的2个乒乓球分成(1,1)放在天平上称,上升的一个就是次品。据此解答。
【详解】这种特产最轻不少于:200-5=195(g)。
第一次称:
把10包产品分成(5,5)两组放在天平上称,找出上升的一组;
第二次称:
把有次品的5包产品分成(2,2,1)三组,把2包一组的放在天平上称,如平衡,则没称的一个是次品;如不平衡,上升的2包产品中有次品;
第三次称:
把上升的2包产品分成(1,1)放在天平上称,上升的一个就是次品;
所以至少称3次就一定能找出次品。
【点睛】本题主要考查了正负数的意义及学生根据天平平衡的原理来解答问题的能力,注意每次取的个数。
6.√
【详解】正负数表示一组相反意义的量;
如:向东记作正,则向西就记作负;
故答案为:√。
7.√
【分析】根据负数的认识,比0小的数叫负数,进行分析。
【详解】所有的负数都比0小,说法正确。
故答案为:√
【点睛】0是正数和负数的分界点,0不是正数也不是负数。
8.√
【分析】根据正负数的定义,比0小的数是负数,比0大的数是正数,据此判断即可。
【详解】由分析可知:
气温0℃比﹣7℃温度高一些,比﹢6℃温度低一些。原题干说法正确。
故答案为:√
【点睛】本题考查正负数,明确正负数的定义是解题的关键。
9.×
【分析】高和低是具有相反意义的量,高于海平面记作“﹢”,那么低于海平面应记作“﹣”,据此解答。
【详解】把海平面看作“0”,高于海平面10米记作“﹢10米”,低于海平面10米应记作“﹣10米”。
故答案为:×
【点睛】掌握正负数的意义和表示方法是解答题目的关键。
10.×
【分析】先确定这种方便面包装质量的合格范围,然后对比,超过范围就不合格,据此判断。
【详解】一种方便面包装质量规定(90±5)克,抽查到一袋重97克,97克>95克,那么这袋方便面不合格,原题说法错误。
故答案为:错误。
【点睛】此题主要考查了正负数的应用。
11.B
【分析】和0的差最小的数,最接近0。据此先求出各个选项中的数和0的差,再选出正确选项即可。
【详解】A.0-(﹣3)=3;
B.0-(﹣1)=1;
C.2-0=2;
D.5-0=5;
3、1、2、5这四个数中1最小,所以﹣1最接近0。
故答案为:B
【点睛】本题考查了正负数,明确正负数的意义是解题的关键。
12.A
【分析】长沙某天的气温是﹣2℃~8℃,则长沙的最低气温是﹣2℃,长沙的最高气温是8℃,则最高气温和最低气温相差10℃。
【详解】8℃与﹣2℃相差10℃。
故答案为:A。
【点睛】本题考查负数,解答本题的关键是掌握负数的概念。
13.A
【分析】根据“规定10吨记为0吨,11吨记为﹢1吨。”可知:以10吨为基准,11吨比10吨多1吨,记作+1吨。即低于10吨的吨数用负数表示,高于10吨的吨数用正数表示。
【详解】A.8吨比10吨少2吨,所以8吨记为-2吨。即8吨记为+8吨是错误的。
B.15吨比10吨多5吨,所以15吨记为+5吨。
C.6吨比10吨少4吨,所以6吨记为-4吨。
D.20吨比10吨多10吨,所以20吨记为+10吨。
故答案为:A
【点睛】用正数和负数表示具有相反意义的量时,要明确“基准”。
14.B
【分析】90分为标准,超过的分数记作正数,不足的分数记作负数,所以﹣3分,就是比标准分少3分。
【详解】根据分析可知90-3=87(分),
故答案为:B
【点睛】正确理解正负数的意义,正负数表示具有相反意义的量。
15.D
【分析】以标准外直径为标准,多于标准外直径记为正,少于标准外直径记为负,据此分析。
【详解】485-482=3(mm),②号零件外直径应记作﹣3mm。
故答案为:D
【点睛】关键是理解正负数的意义,正负数表示意义相反的量。
16.见详解
【分析】向东行为“正”,则向西行为“负”,直接得出结论即可。
【详解】①他从少年宫向西行80米,表示为﹣80米。
②聪聪现在的位置是+36米,说明他在少年宫的东边36米。
【点睛】本题主要考查用正负数来表示具有意义相反的两种量。
17.28分;能晋级
【分析】以6分为标准,高于6分记为正,低于6分记为负,分别求出4个评委打的分数,加起来,与25分比较。
【详解】6+2=8(分)
6-1=5(分)
6+3=9(分)
8+6+5+9
=14+5+9
=19+8
=28(分)
28>25
答:小明的总分数是28分,能晋级。
【点睛】本题考查了正负数的意义和应用,正负数可以表示相反意义的量。
18.(1)东; 40;(2)(3)题如下图。
【分析】根据题意,规定向东为正,则向西为负,据此解答即可。
【详解】(1)规定向东为正,所以﹢4说明向东走了4格,4×10=40(m);
(2)40÷10=4,从0处向西走即向西走4格;
(3)从0处出发,先走,再走,即先向西走2格再向东走7格,最后在0处往东5格处。
(2)(3)作图如下:
【点睛】明确对于具有相反意义的量,规定其中一个量为正,则另一个为负。
19.(1)星期二生产的零件个数最多,是112个;
(2)104个零件
【分析】负数表示比标准数量少,正数表示比标准数量多。据此解答。
【详解】(1)从上面的记录中看出他在星期二生产的零件个数最多,因为+12>+9>+8>﹣3>﹣6; 100+12=112(个);
答:星期二生产的零件个数最多,是112个。
(2)100×5+[(﹣6)+12+9+(﹣3)+8]
=500+20
=520(个)
520÷5=104(个)
答:小张平均每天生产了104个零件。
【点睛】本题考查正负数的应用,明确正负数的意义是解答此题的关键。
20.(1)3:00;12:00
(2)不合适;因为北京时间17:00是旧金山时间的1:00,正处于凌晨。
【分析】(1)正数表示在北京时间向后推几个小时,即加上这个正数,负数表示在北京时间向后前推几个小时,即加上这个负数;
(2)计算出旧金山的时间,然后判断即可。
【详解】(1),即伦敦时间3:00
,即东京时间12:00
(2),即旧金山时间1:00
所以不合适,因为旧金山时间是凌晨1:00,姨妈可能正在休息。
【点睛】此题是典型的正数与负数的实际运用问题,应联系实际生活,认清正数与负数所代表的实际意义。
