18.2.3 正方形 同步练习题(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.2.3 正方形 同步练习题(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 284.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 13:32:55 | ||
图片预览


文档简介
第十八章 平行四边形
18.2.3 正方形
一、选择题
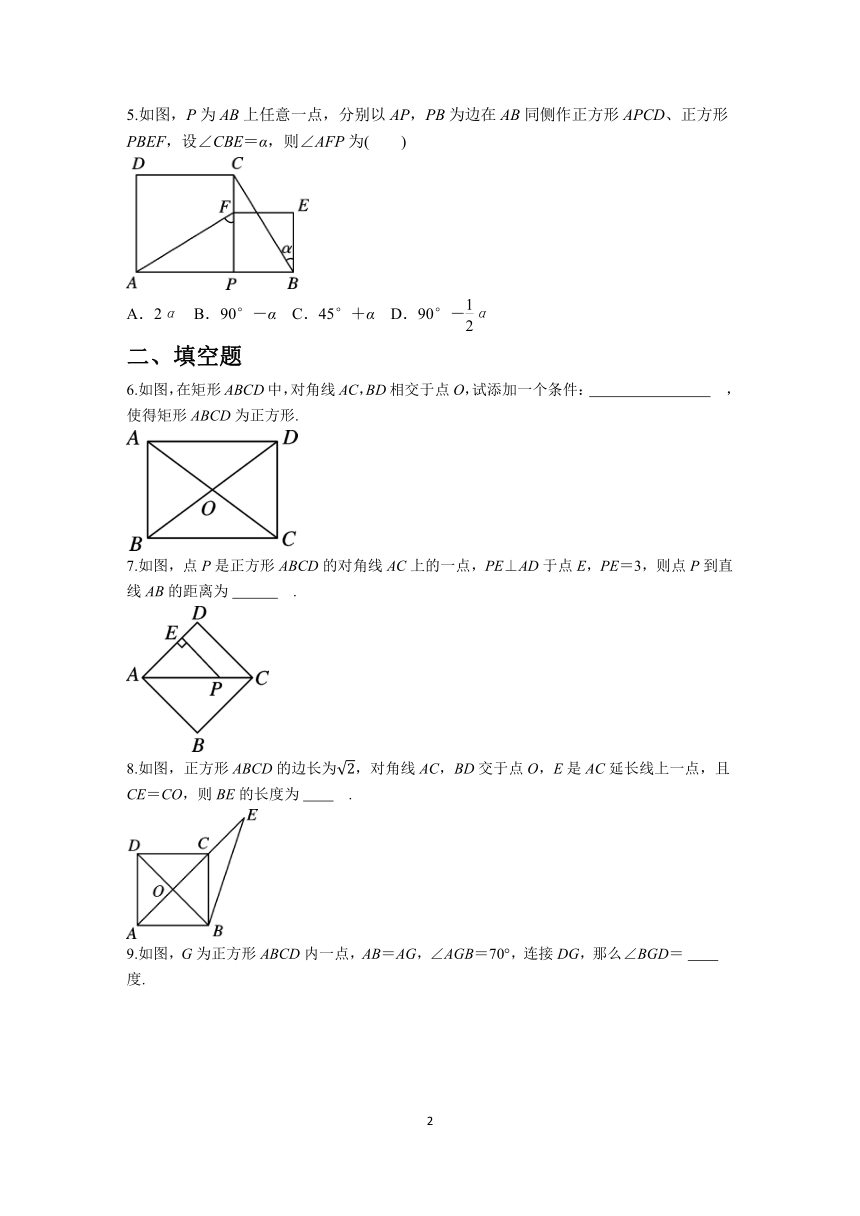
1.如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是( )
A.(3,-3) B.(-3,3)
C.(3,3) D.(-3,-3)
2.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
4.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( )
A.80° B.90°
C.105° D.115°
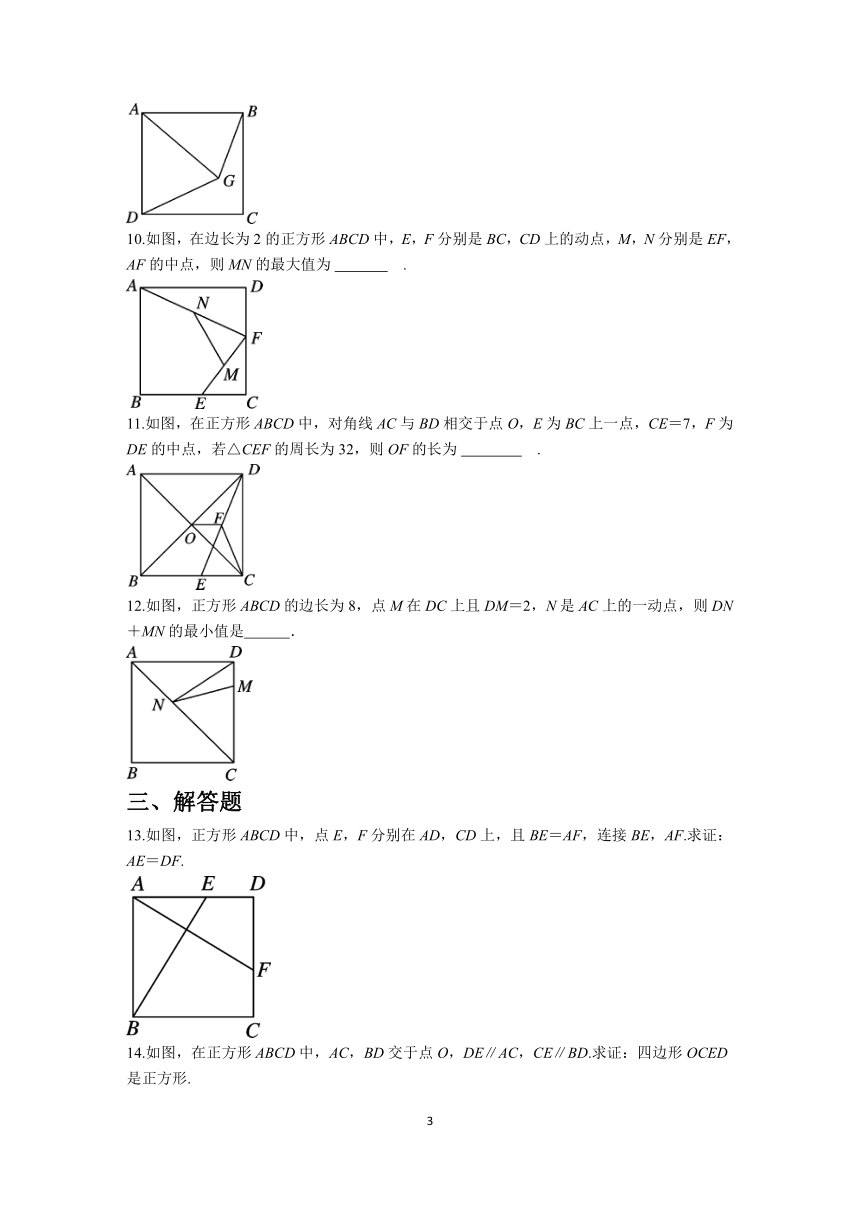
5.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°-α C.45°+α D.90°-α
二、填空题
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,试添加一个条件: ,使得矩形ABCD为正方形.
7.如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
8.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为 .
9.如图,G为正方形ABCD内一点,AB=AG,∠AGB=70°,连接DG,那么∠BGD= 度.
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,则OF的长为 .
12.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
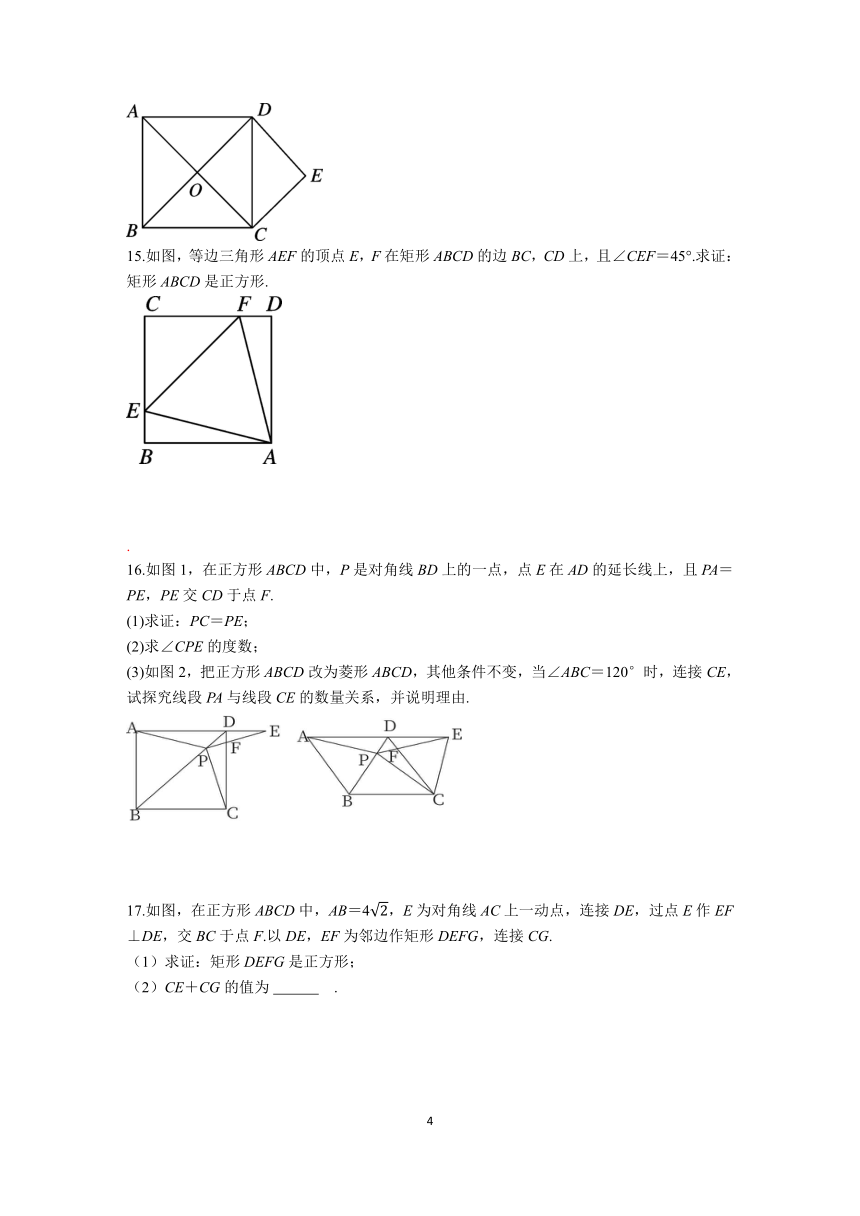
13.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
14.如图,在正方形ABCD中,AC,BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是正方形.
15.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
.
16.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
17.如图,在正方形ABCD中,AB=4,E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F.以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)CE+CG的值为 .
1
参考答案
一、选择题
1.如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是( C )
A.(3,-3) B.(-3,3)
C.(3,3) D.(-3,-3)
2.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( A )
A.9 B.12 C.15 D.20
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( C )
A.10° B.15° C.20° D.30°
4.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( C )
A.80° B.90°
C.105° D.115°
5.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( B )
A.2α B.90°-α C.45°+α D.90°-α
二、填空题
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,试添加一个条件: ,使得矩形ABCD为正方形.
【答案】AB=AD(答案不唯一)
7.如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
【答案】3
8.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为 .
【答案】
9.如图,G为正方形ABCD内一点,AB=AG,∠AGB=70°,连接DG,那么∠BGD= 度.
【答案】135
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
【答案】
11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,则OF的长为 .
【答案】
12.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
解析:连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
13.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,
AB=AD,
在Rt△BAE和Rt△ADF中,
∴Rt△BAE≌Rt△ADF(HL),
∴AE=DF.
14.如图,在正方形ABCD中,AC,BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是正方形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是正方形,
∴OC=OD,OC⊥OD.
∴ OCED为正方形.
15.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD(AAS).∴AB=AD.
∴矩形ABCD是正方形.
16.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
解:(1)易证△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)∠CPE的度数为90°.
(3)PA=CE.
理由:易证△EPC是等边三角形,
∴PC=PE=CE.
∵PA=PE,∴PA=CE.
17.如图,在正方形ABCD中,AB=4,E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F.以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)CE+CG的值为 .
解:(1)证明:如图所示,过点E作
EM⊥CD于点M,EN⊥BC于点N,
∵四边形ABCD是正方形,
∴∠ACB=∠ACD.
∵EM⊥CD,EN⊥BC,∴EM=EN.
∵∠EMC=∠ENC=∠BCD=90°,
∴四边形EMCN是矩形.∴∠MEN=90°.
∵四边形DEFG是矩形,∴∠DEF=90°.
∴∠DEM=∠FEN.
∵EM=EN,∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA).∴ED=EF.
∴矩形DEFG是正方形.
(2)8
18.2.3 正方形
一、选择题
1.如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是( )
A.(3,-3) B.(-3,3)
C.(3,3) D.(-3,-3)
2.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
4.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( )
A.80° B.90°
C.105° D.115°
5.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°-α C.45°+α D.90°-α
二、填空题
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,试添加一个条件: ,使得矩形ABCD为正方形.
7.如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
8.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为 .
9.如图,G为正方形ABCD内一点,AB=AG,∠AGB=70°,连接DG,那么∠BGD= 度.
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,则OF的长为 .
12.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
13.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
14.如图,在正方形ABCD中,AC,BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是正方形.
15.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
.
16.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
17.如图,在正方形ABCD中,AB=4,E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F.以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)CE+CG的值为 .
1
参考答案
一、选择题
1.如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是( C )
A.(3,-3) B.(-3,3)
C.(3,3) D.(-3,-3)
2.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( A )
A.9 B.12 C.15 D.20
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( C )
A.10° B.15° C.20° D.30°
4.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( C )
A.80° B.90°
C.105° D.115°
5.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( B )
A.2α B.90°-α C.45°+α D.90°-α
二、填空题
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,试添加一个条件: ,使得矩形ABCD为正方形.
【答案】AB=AD(答案不唯一)
7.如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
【答案】3
8.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为 .
【答案】
9.如图,G为正方形ABCD内一点,AB=AG,∠AGB=70°,连接DG,那么∠BGD= 度.
【答案】135
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
【答案】
11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,则OF的长为 .
【答案】
12.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
解析:连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
13.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,
AB=AD,
在Rt△BAE和Rt△ADF中,
∴Rt△BAE≌Rt△ADF(HL),
∴AE=DF.
14.如图,在正方形ABCD中,AC,BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是正方形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是正方形,
∴OC=OD,OC⊥OD.
∴ OCED为正方形.
15.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD(AAS).∴AB=AD.
∴矩形ABCD是正方形.
16.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
解:(1)易证△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)∠CPE的度数为90°.
(3)PA=CE.
理由:易证△EPC是等边三角形,
∴PC=PE=CE.
∵PA=PE,∴PA=CE.
17.如图,在正方形ABCD中,AB=4,E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F.以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)CE+CG的值为 .
解:(1)证明:如图所示,过点E作
EM⊥CD于点M,EN⊥BC于点N,
∵四边形ABCD是正方形,
∴∠ACB=∠ACD.
∵EM⊥CD,EN⊥BC,∴EM=EN.
∵∠EMC=∠ENC=∠BCD=90°,
∴四边形EMCN是矩形.∴∠MEN=90°.
∵四边形DEFG是矩形,∴∠DEF=90°.
∴∠DEM=∠FEN.
∵EM=EN,∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA).∴ED=EF.
∴矩形DEFG是正方形.
(2)8
